基于比例積分微分的電機滑模變結構同步控制
陳紅紅,任立勝
(內蒙古農業大學,內蒙古 呼和浩特 010018)
1 引言
滑模變結構屬于電機的重要組成部分,對其控制不當會造成逆變器開關頻率不恒定、滑模變結構脈動過大從而引起噪聲現象。而滑模變結構控制是在矢量控制的基礎上發展起來的高性能調速方法,重點突出對滑模變結構的直接控制能力,因此在電機控制領域應用較為廣泛。傳統算法對滑模變結構進行控制時,由于控制系統結構與參數變化性較強,不能獲取理想控制指標,使之出現滑模變結構脈動大的缺陷,導致系統失穩。為滿足電機滑模變結構控制要求,相關學者提出下述方法。
文獻[1]提出一種改進的滑模觀測器,采集電機位置信號,通過電機的轉速構建滑模觀測器。文獻[2]提出基于自抗擾速度控制的電機滑模變結構同步控制方法。通過滑模變結構構建滑模控制器。引入Super-twisting算法,構建負載轉矩觀測器,并利用Super-twisting定子提升觀測精度。上述兩種滑模變結構控制方法雖然達到抑制電機滑模變結構脈動目的,但是調節時間過長,運行效率較低,只在低轉速情況下適用。
針對上述方法存在的問題,通過對比例積分微分[3]研究電機滑模變結構同步控制。根據電機的物理模型與負載模型,獲取PID控制器傳遞函數,并對影響控制性能的參數進行考慮;在積分增益、微分增益基礎上對PID改進,結合抗積分飽和算法,改善對誤差反應速度和靈敏度,確定最后PI控制方式。仿真結果表明,所提方法可以解決電機滑模變結構負載變化與非線性干擾導致的誤差,減小超調量和調節時間,提高響應速度。
2 電機與負載模型構建
2.1 電機模型
無論是異步還是同步電機,通過向量變化、磁鏈定向與電流閉環操作后都能等效為直流電機。以下表示直流電機的數學模型

(1)
式中,usd、usq與φsd、φsq分別表示d、q軸上的電壓與磁鏈;If代表虛擬勵磁電流;Rs表示定子繞組;Lsd與Lsq是等效定子繞組自感[4],Lmd描述d軸電樞反應電感。
式(1)中的變量符合式(2),如果利用轉子磁鏈進行定向控制,則由式(2)可以獲得式(3)
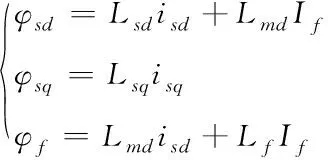
(2)
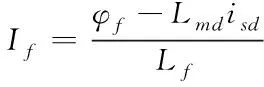
(3)
電機的物理模型如下圖所示,假設控制定子電流向量在q軸上,且isd=0,isd=is,則電磁滑模變結構方程如式(4)所示,因此通過對定子電流的控制能夠實現對電磁滑模變結構控制。將電流環等效于時間常數是Ti的慣性環節,獲取式(5)。

圖1 電機物理模型圖
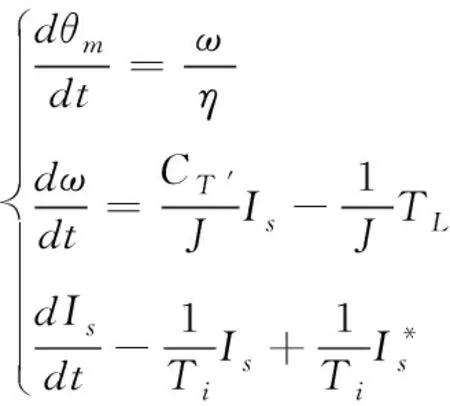
(5)
從上述公式中可以看出直流和交流電機均存在統一數學模型[5]。
2.2 負載模型
在閥門運行過程中,系統中的摩擦滑模變結構、扭簧彈力與瞬態排氣壓力波動均會作用在電機軸端。這時系統運動方程如下:

(6)
式(6)中,J表示電機軸上產生的轉動慣量,f是粘性摩擦系數,F1代表閥門上形成的排氣壓力,F2為摩擦力,S則為力臂,Tf是電機制動滑模變結構,Tk描述彈簧滑模變結構。
此時,電機負載模型表示為
Tk=Kθ+T0
(7)
式(7)中,K為扭簧滑模變結構系數,T0表示初始滑模變結構。
3 比例積分微分的電機滑模變結構控制
3.1 PID控制原理分析
在控制系統中,控制器的精準度與穩定性會對系統性能產生較大影響,但是二者之間又互相矛盾[6]。如果提高系統精準度,則穩定性很難達到要求,會出現較大擾動;如果穩定性得到提高,系統準確度又會偏離設計條件。所以需要在控制系統基礎結構之上設置附加裝置,實現準確性與穩定性的平衡。在整體系統中,將固有且不能改變的部分稱為固有環節,把為提高系統性能才添加的部分稱為校正環節。
開環系統表示系統的輸出屬于一個開源的、不受任何控制的信號。閉環系統指的是輸出受到限制不能隨意變化,把輸出誤差當作調制器的調節量,以此提高輸出的準確性。
針對控制系統而言,在利用單位負反饋控制時,系統產生的偏差信號屬于最原始、最基礎的信號,為實現系統不同指標之間的平衡需要對這些偏差信號進行計算,從而獲取校正過程的控制規律。在實際控制中,最基礎校正環節控制規律是PI控制與滯后校正[7]。
PID控制利用比例、積分、微分環節共同作用,根據系統誤差偏離值在通過調整后輸出實時控制量實現對系統的穩定控制。其具有結構簡單、性能穩定等優勢,因此在控制領域屬于關鍵校正技術。在系統偏差這個初始信號基礎上,通過比例環節、積分與微分環節獲取控制量,消除誤差,從而使系統性能達到要求。
PID具有改善系統動態響應程度,消除靜態誤差的作用。微分控制使開環傳遞函數多出一個零點,緩解系統暫態響應,并在S平面原點添加一個極點,使系統穩態誤差降至零。一般情況下在持續的S域內可以通過系數傳遞函數表示PID控制器
G(S)=KP+Ki/S+KPS
(8)
還可以表示為
G(S)=Kp(1+1/T1S+TbS)
(9)
式(8)、式(9)中,Kp表示比例增益,Ki屬于積分常數,T1與Tb分別代表積分和微分時間常數。
以此獲得PID控制器的輸出為
u(t)=Kp+Kie(t)dt+KDde(t)/dt
(10)
通常情況下,PID控制器起到調節作用,所以其調節能力必須要重點考慮,為獲取PID的最佳性能參數Kp、Ki與KD,必須結合一些規則來尋找問題最優解。例如IGE、ISE、ITSE以及ITAE規則,將其構成四種目標函數表示為

(11)

(12)

(13)

(14)
PID控制的實質就是使上述目標函數J變為最小從而減少超調量[8]。
3.2 觀測器參數對控制性能影響研究
LESO為PID控制器的核心,其參數取值會影響到控制性能。
三階LESO傳遞函數表示為
(15)


(16)
綜上所述,確定LESO的誤差方程表示為
(17)
由式(17)可知,對于e1和e2來說,ωr值越大,響應放大系數相應減小,LESO調節精度越高,但是對于ωr來說,ωr屬于其傳遞函數中的截止頻率,該頻率越大,系統抗干擾性能越強。與此同時,-ωr是傳遞函數的極點,ωr越大極點則越小,這時系統響應速度提升,相位滯后程度小[9]。
經過以上描述可知,ωr值越大,控制性能與抗干擾性越強。
3.3 PID積分與微分的改進
傳統PID控制器在時域中能夠利用下述公式進行表示

(18)
經過整定的參數在全部控制過程中不會發生改變,通過理論分析表明,此種控制器不能同時滿足控制參考輸入與抗干擾的要求,而且會出現快速性與超調量之間的矛盾。為避免矛盾發生,在改進積分與微分基礎上得到變結構PID控制器。其能夠結合系統誤差對控制器參數與結構進行實時修正,提高響應速度,改善穩態精度。
3.3.1 比例增益
比例增益Kp的取值隨誤差的大小發生改變,如果誤差較大,則對應取值較大,這樣不僅能提高響應速度,而且還能避免超調量過大,確保控制系統穩定性。
Kp(e)=ap+bp(1-exp(-cp|e|))
(19)
式中,ap,bp與cp表示正實常數,e代表誤差。
如果比例增益設置過大,會降低系統響應時間,破壞系統穩定性。
3.3.2 積分增益
積分增益由兩個因子構成分別為:積分主增益Ki與變增益Ki0。在存在較大誤差時,Ki較小,甚至等于零,避免出現震蕩與積分飽和現象,降低超調量,減少控制時間;由于誤差逐步減小,Ki變大,以此去除穩態誤差。Ki0在較小誤差區間內對Ki進行放大,用作提高積分作用,改善系統抗干擾性能。
積分主增益Ki的表達式如下所示
Ki(e)=aiexp(-ci|e|)
(20)
積分變增益Ki0表達式為
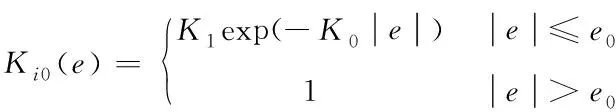
(21)
式中,K0,K1與e0均為正實數。
為確保Ki0呈持續平滑變化[10],則K0,Ki與e0需要符合下述條件
K1exp(-K0e0)=1
(22)
3.3.3 微分增益
如果誤差較小,則微分增益需要取較大值,反之,取最小值。這樣可以提高對誤差的反應速度,改善控制器對干擾的靈敏度。
Kd(e)=ad-bd(1-exp(ed|e|))
(23)
式(23)中,ad,bd與ed都屬于整實數,且滿足ad>bd的條件。
3.4 電機滑模變結構控制方程建立
在對積分與微分進行改進后,由于電機工作環境溫度較高,如果持續大電流工作會導致電機損壞,因此必須引入電流限幅。因為電流和電壓存在一定關系,可以將其近似為電壓幅值,表達式如下所示
umax(t)=f(ta,T)
(24)
式中,umax(t)表示任意時間點上的最大電壓值,ta代表所處環境溫度,T描述持續時間。
在出現電壓限幅時,系統因為持續較長時間出現一個方向偏差,PID控制器的輸出在積分作用影響下不斷累積導致到u(t)達極限位置而進入飽和區域。這時,如果出現反向誤差,必須使u(t)退出飽和區域,才可以使系統響應。引入抗積分飽和方法過程中,若出現u(t-1)>umax(t)現象時,為避免積分飽和,積分項只對負偏差進行累加;在出現u(t-1) un(t-1)=(umin(t),((u(t-1)+ua,umax))) (25) 式(25)中,ua表示模型預測電壓,u(t-1)代表前一次PID控制器沒有進行電壓限幅時的輸出值,un(t-1)為前一次控制器經過電壓限幅后產生的輸出值,umax描述任意時間點上電壓最大值,umin(t)=-umax(t)。 在實際控制過程中,PID調節方法中最常用的是PI控制,結合改進的微分與積分,確定最終PI控制器電機滑模變結構控制方程如下所示 當u(t-1)=us(t-1)時 (26) 當u(t-1)≠us(t-1)時 (27) 在控制環節,理想輸出信號與輸入信號無限靠近,即誤差信號越小,控制系統精準度越高。 為驗證所提基于比例積分微分的電機滑模變結構同步控制方法的有效性,設計實驗。實驗中被控制目標為開關磁阻電機,它的功率為5kW,額定電流與額定電壓分別為25A與110V,轉動慣量是0.002kg·m2,飽和與非飽和電感分別為3500μH與200μH,并對系統延時步數進行設計k=1,采樣時間間隔為0.4s,控制時域長度pu=15,控制量變量加權為λ=0.2。 引入滑模變結構系數對滑模變結構脈動大小進行衡量,定義式如下: (28) 式(28)中,Tmax,Tmin與Tav分別代表最大、最小和瞬時滑模變結構瞬時轉速與平均滑模變結構瞬時轉速。 為更好體現本文方法優越性,采用文獻[1]方法、文獻[2]方法作為實驗對比方法,得到不同方法的超調量與調節時間如表1所示。 表1 不同方法控制效果對比表 分析表1可知,文獻[1]方法及文獻[2]方法的滑模變結構控制超調量較大,調節時間較長,而所提方法的超調量僅為1%,調節時間為0.78s,說明所提方法具有較好的控制效果。 在此基礎上,分析3種方法控制下的轉矩輸出性能,得到對比結果如圖2所示。 圖2 不同方法控制輸出對比圖 從圖2可以看出,文獻[1]、文獻[2]方法的轉矩輸出波動較大,而所提方法的轉矩輸出較穩定;根據實驗結果可知,文獻[1]方法的轉矩輸出平均值為42N·m,文獻[2]方法的轉矩輸出平均值為36N·m,而所提方法的轉矩輸出平均值為23N·m。實驗結果表明,所提方法的轉矩輸出較穩定,輸出值較小,達到了理想控制效果。 為實現對電機滑模變結構的有效控制,改善滑模變結構脈動過大現象,提出基于比例積分微分的電機滑模變結構同步控制方法。在建立電機模型與負載模型基礎上分析PID控制器原理;研究參數對控制性能影響,通過對積分與微分的增益提高對控制誤差反應的靈敏度,引入電流限幅,獲取抗積分飽和變結構公式,完成對PID的改進,達到滑模變結構控制目的。實驗結果證明所提方法可以有效搜索到控制最佳參數,動態性能良好,適應性較強,明顯改善滑模變結構脈動過大的缺陷,有望更好地實現對電機滑模變結構的同步控制。
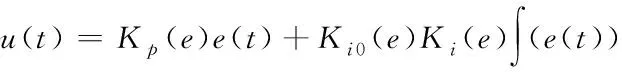
4 仿真數據分析與研究
4.1 實驗環境及參數設置
4.2 方法與結果討論



5 結論

