基于自適應無跡卡爾曼濾波QAR數據降噪研究

錢 宇，王立新

(中國民用航空飛行學院，四川 廣漢 618307)

1 引言

隨著科學技術的不斷發展，飛行數據記錄設備也在不斷更新升級，數據的采集數量與質量都有很大提高。快速存取記錄器(Quick Access Recorder， QAR)記載著各種飛行參數， QAR數據分析與挖掘日益受到航空公司及航空監管部門的關注。然而，傳感器記錄數據難免會受各種因素的干擾，導致譯碼后數據包含大量異常值。QAR數據有效性分析對航空公司安全運營有著極其重要的影響，為給數據分析與挖掘工作提供更可靠的數據支撐，需要對譯碼后的數據進行處理，提高QAR數據的可靠性[1-2]。

目前，很多學者在QAR數據處理方面展開深入研究。張鵬等[3]采用時間序列對QAR數據特征進行預測。楊慧等[4]介紹聚類的方法，QAR數據異常點檢測問題被有效地解決。陳聰等[5]提出平穩小波法對QAR數據進行降噪噪處理。針對大量飛行數據不能被有效利用的問題，巴塔西等[6]提出采用時間序列法進行故障預測。基于飛機在高海拔機場進近過程的QAR數據，汪清等[7]采用擴展卡爾曼濾波對相關參數進行估計。然而，上述研究存在如下不足：1)聚類法不能有效的剔除野值，時間序列法對非平穩趨勢數據預測效果較差。2)小波法、卡爾曼濾波對非線性數據無法起到好的降噪效果，擴展卡爾曼濾波對非線性數據無法精準估計且穩定性較差。3)傳統卡爾曼濾波只考慮了高斯白噪聲，這樣在未知干擾環境噪聲[8]的情況下，降噪效果會變差。

研究利用改進拉依達準則和自適應無跡卡爾曼濾波對QAR數據降噪處理。變換貝塞爾公式對拉依達準則改進，提高了數據精度，使自適應無跡卡爾曼濾波對數據降噪免受粗大誤差干擾；引入自適應噪聲估計器的無跡卡爾曼濾波算法，有效解決了對非平穩數據預測效果差、非線性數據降噪效果差及估計精度低的問題。利用空客A330飛機的兩組數據樣本對本文提到的方法仿真實驗，結果表明該方法可有效解決數據包含異常值的問題。

2 數學方法描述

2.1 拉依達準則

拉依達準則(Pauta)被用來檢測數據中的粗大誤差，要求數據量大，它以99.7%為參考標準確定置信區間范圍并計算標準偏差，凡超越此區間的誤差歸為粗大誤差應被剔除。

1)計算算術平均值

yi=xi+x0

(1)

(2)

由式(1)和(2)得算術平均值為

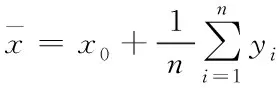
(3)

2)計算標準偏差

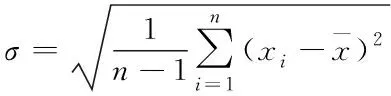
(4)

(5)

2.2 AUKF算法

為提高對非線性系統的濾波效果，Julier等人提出無跡卡爾曼濾波算法[10-11]，采用對非線性系統濾波的方法，而非傳統的線性化方式。它對線性系統也能起到很好的濾波效果[12]。

1)UKF算法實現

UT變換過程如下：

①產生Sigma點

(6)

②計算權值

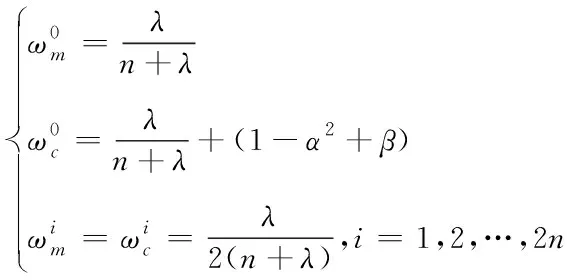
(7)

UKF非線性系統為：

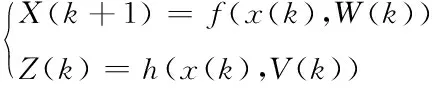
(8)

式(8)中，f為非線性狀態方程函數，h為非線性觀測方程函數，W(k)和V(k)為協方差矩陣Q和R的高斯白噪聲。

UKF的具體推導步驟如下：

①獲取采樣點并計算權值

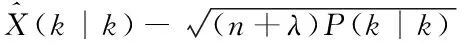
(9)

②計算一步預測

X(i)(k+1|k)=f[k，X(i)(k|k)]

(10)

③計算一步預測及協方差矩陣

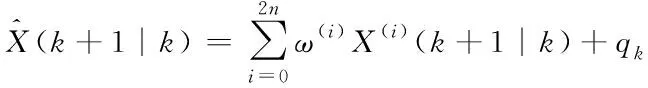
(11)

(12)

④二次利用UT變換，得到新的Sigma點集

X(i)(k+1|k)=

(13)

⑤計算觀測量

Z(i)(k+1|k)=h[X(i)(k+1|k)]

(14)

⑥計算系統預測的均值及協方差

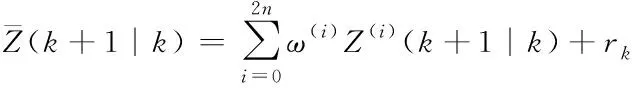
(15)

(16)

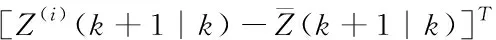
(17)

⑦計算Kalman增益矩陣

(18)

⑧計算系統的狀態更新和協方差更新

(k+1|k+1)=(k+1|k)+

K(k+1)[Z(k+1)-(k+1|k)]

(19)

P(k+1|k+1)=P(k+1|k)-

K(k+1)PZkZkKT(k+1)

(20)

由以上步驟可以看出，UKF對非線性濾波是在估計點附近進行UT變換，計算Sigma點集的均值及方差，再對其進行非線性映射，求得狀態概率密度函數，無需在估計點處做Taylor級數展開及前n階近似，計算更為簡單。

2)AUKF算法實現

傳感器在記錄飛行數據過程中，由于各種因素的影響，譯碼后的QAR數據可能包含其他噪聲值，這樣勢必會增大濾波降噪的偏差。為了解決此問題UKF算法結合Sage-Husa濾波算法構成AUKF算法[13-14]，Sage-Husa自適應濾波器可使系統在利用原始數據進行濾波降噪的同時，對系統噪聲方差進行實時修正[15-17]，大大提高了濾波降噪的精度和有效性。自適應噪聲估計器遞推過程如下

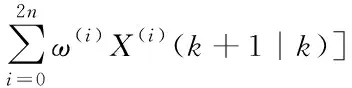
(21)

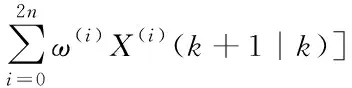
(22)

(23)

(24)

εk+1=Zk+1-k+1

(25)

(26)

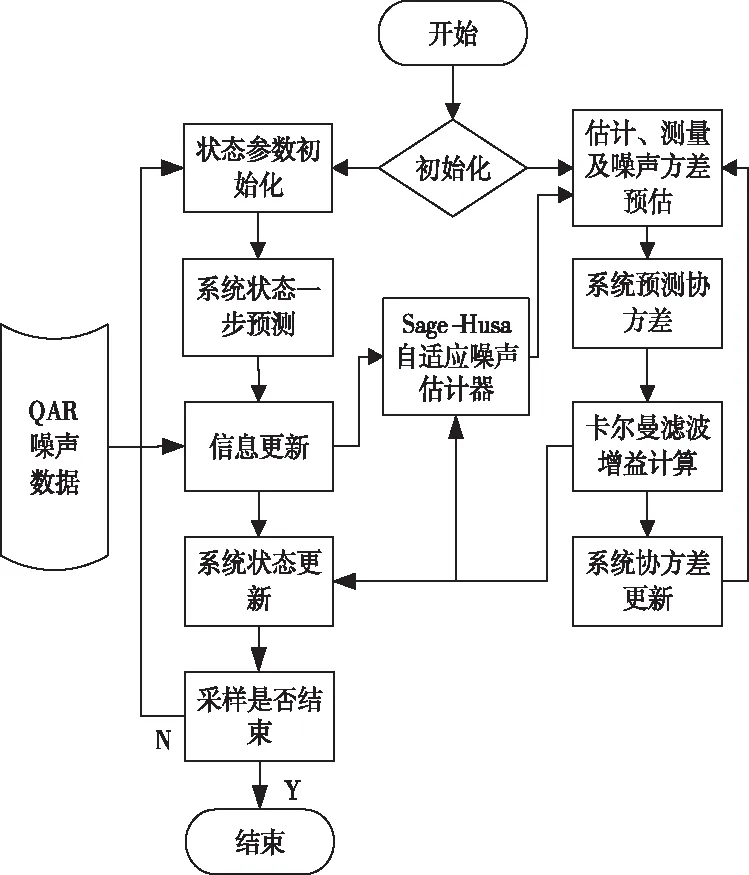
圖1 自適應無跡卡爾曼濾波降噪流程圖

3 仿真算例

研究采用空客A330飛機某次飛行任務的兩組QAR譯碼數據作為樣本數據，分別選擇真空速、偏流角各150個數據，驗證算法的可行性。

3.1 樣本數據檢測與剔除

采用改進拉依達準則檢測并剔除粗大誤差數據之前，需要檢驗數據是否滿足拉依達準則的適用條件，要求數據大致符合正態分布、數據量充分大。仿真實驗數據量分別為150，滿足數據量要求；根據QAR數據精度高的特點，由于QAR數據精度比較高，選擇2倍標準偏差作為判斷標準，|gi|>2σ時，xi為粗大誤差剔除，|gi|≤2σ時，xi為正常值保留。此時概率區間為95%，兩組樣本數據95%置信區間圖如圖2。

圖2 樣本數據置信區間圖

由圖2可以看出，兩組數據基本都分布在95%概率區間內，驗證了數據大致符合正態分布，滿足拉依達準則的適用條件。研究分別采用傳統和改進拉依達準則檢測兩組數據中的粗大誤差，并對其進行標記及剔除，處理結果如圖3。

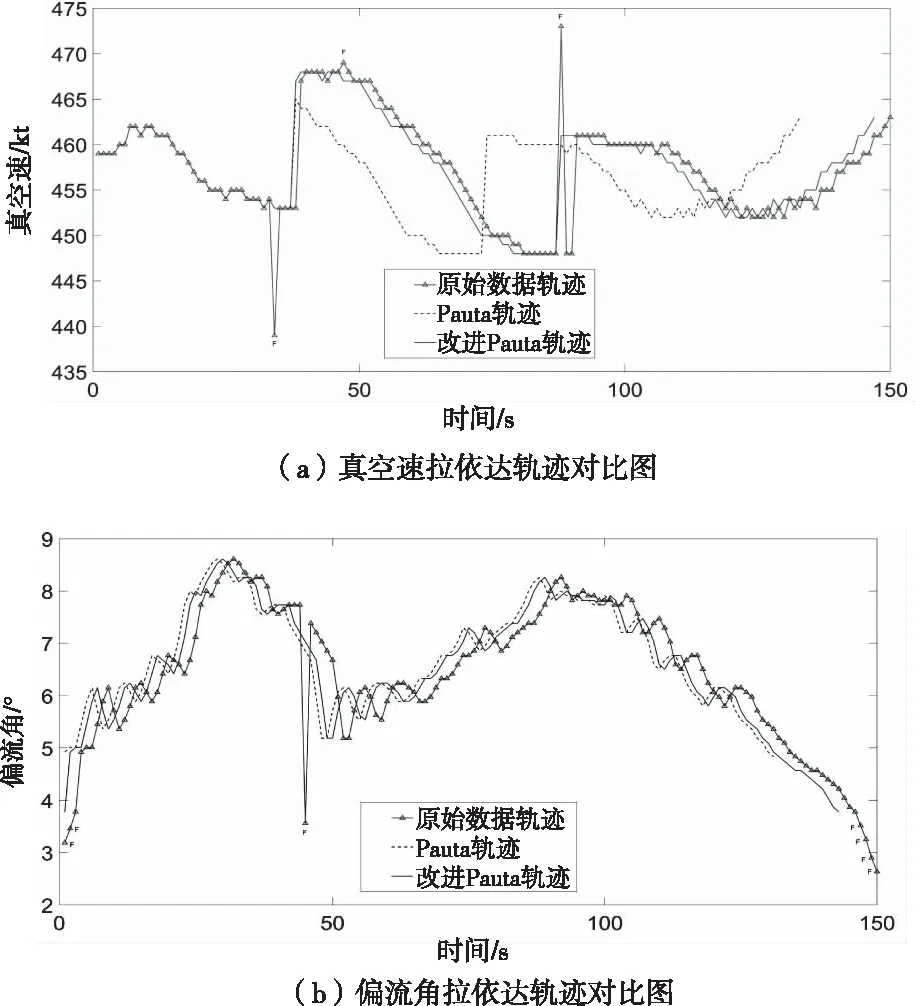
圖3 拉依達軌跡對比圖

由圖3可以看出，傳統及改進拉依達準則都能有效檢測并剔除誤差數據，傳統拉依達準則循環剔除粗大誤差后，積累誤差增大，這樣會剔除一些隨機誤差數據，而改進拉依達準則在剔除粗大誤差數據的情況下，保留了更多有用數據，避免丟失更多數據信息。傳統和改進算法處理后的數據量信息見表1。

表1 拉依達準則處理前后數據量對比

(27)

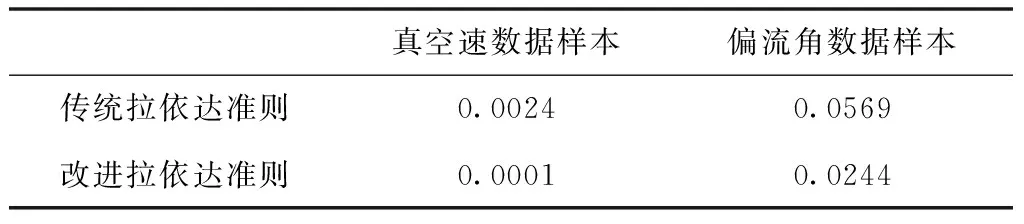
表2 樣本數據相對偏差對比

從表2的數據可以看出，采用改進拉依達準則處理的兩組數據相對偏差更小，說明改進比傳統算法處理數據的準確性更高，驗證了改進算法的有效性。

3.2 AUKF與UKF降噪對比

兩組數據樣本經改進拉依達準則處理，提高了數據的可靠性。然而傳感器在記錄數據的過程中，可能受到各種因素影響，導致譯碼后數據包含噪聲，運用AUKF算法對QAR數據進行降噪處理，更能提高數據的可靠性。

AUKF較UKF優勢在于加入了自適應濾波器，在實際應用中數據包含的噪聲不一定是高斯白噪聲，噪聲值也可能會實時的發生變化，傳統的UKF降噪的效果就會變差。根據兩組數據的實際情況，Q=0.01，R=0.25，遺忘因子b=0.96，這樣濾波降噪效果更好，兩組數據UKF濾波、AUKF濾波擬合曲線及濾波偏差對比如圖4和圖5。

圖4 UKF與AUKF軌跡對比圖

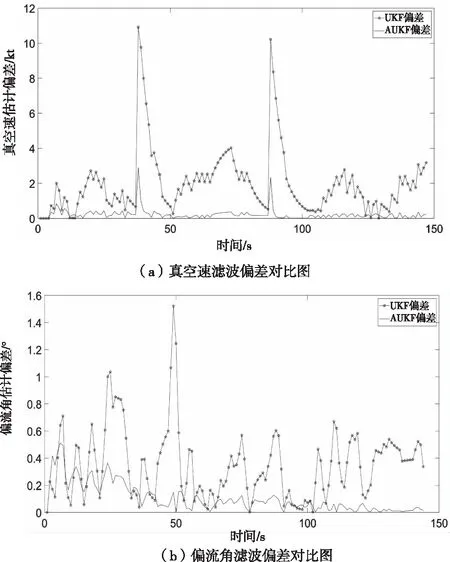
圖5 UKF與AUKF濾波偏差對比圖

從圖5可以看出，濾波后的曲線更加平滑，說明UKF和AUKF對數據降噪處理是有效的，UKF濾波曲線比AUKF濾波曲線更偏離原始數據軌跡；從圖6可以看出AUKF偏差更小，說明經AUKF處理的數據更接近于真實值，更可靠。下面利用均方根誤差、信噪比及平滑度指標對UKF和AUKF濾波降噪效果進行評估，兩種算法的對比評估具體見表3和表4。

表3 真空速UKF、AUKF降噪效果評估

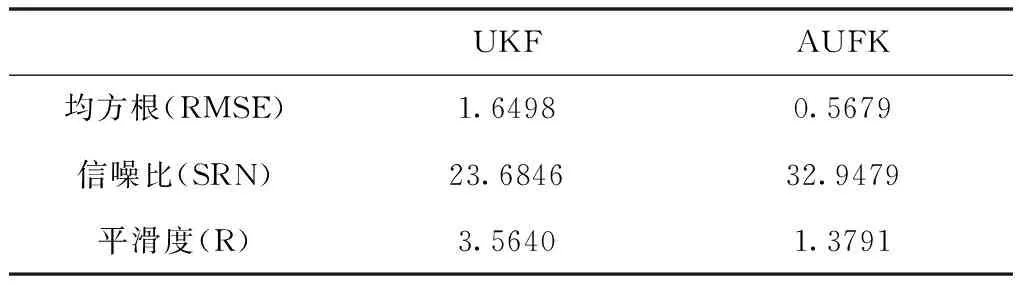
表4 偏流角UKF、AUKF降噪效果評估

根據表3和4可知，兩組數據UKF得到的信噪比小于AUKF，均方根誤差大于AUKF，說明AUKF對原始數據的處理保留了其更多的有效信息而抑制了更多噪聲；從平滑度指標來看，兩組數據UKF濾波后平滑度均大于AUKF，說明UKF濾波處理后的數據波形比AUKF濾波更加平滑，但這也從側面反應經過AUKF處理過的數據相比UKF處理過的數據而言更逼近原始數據，提高了數據的可靠性。

4 結論

1)QAR數據降噪前，需要剔除誤差數據，避免其影響降噪效果。傳統拉依達準則不能精準剔除粗大誤差數據，改進算法在高效、精確剔除誤差數據的前提下，保留了更多數據信息。

2)AUKF較UKF加入了噪聲估計器，可在線估計系統噪聲協方差，抑制初始值偏差及系統噪聲特性未知對濾波降噪穩定性的影響，估計誤差值更小，原始數據的數據信息被最大限度的保留。

3)AUKF收斂速度更快，通過兩組數據仿真結果證明了AUKF更適用于QAR數據降噪，為數據分析提供了更加可靠的數據基礎，這種數據處理方法也具有一定的現實意義。