基于牛頓迭代算法的分形圖像紋理細節增強

余 暉，胡凌燕

(南昌大學信息工程學院，江西 南昌 330031)

1 引言

作為非線性科學研究分支的分形理論主要研究自然界與非線性系統里的不光滑、不規則幾何形體，且該理論被廣泛應用于物理、地質、計算機科學、材料科學以及其它工程技術領域中。計算機圖形學的普及應用與蓬勃發展，推動了一系列抽象圖形與人造物體的形態展示力，但仍無法有效仿真不規則圖形與自然界景物，在不規整形體圖形中引入分形理論與牛頓迭代算法，能夠繪制出絢麗多彩的分形圖形。分形就是將一個零碎或粗糙的幾何形狀劃分為多個部分，各部分均與縮小整個圖形的形狀類似，也就是說，分形有自相似屬性。牛頓迭代算法通過計算機迭代，可以獲取更加復雜的分形結構、更加豐富的顏色、更多的信息以及更強的防偽屬性。圖像的前期預處理中要增強圖像信息，以此達到突出圖像可用細節、噪聲去除、放大不同物體特征差異以及優化視覺效果等目的，該項技術作為圖像處理的關鍵環節，關注度越來越高，也得到了以下具有代表性的研究成果。

文獻[1]提出基于結構層與紋理層分離的圖像增強方法，劃分圖像為紋理層與結構層后，針對結構層，采用累積分布函數，創建具有參數自適應性的Gamma校正算法，增強圖像該層的亮度與對比度，針對紋理層則通過高頻分量提升法增強紋理細節，將兩層結合后即為增強后圖像；文獻[2]提出基于簡化大氣散射模型的單幅紅外圖像增強方法。該方法采用圖像景深模型架構參考圖，通過聚類策略分割成數個景深近似場景，經簡化大氣散射模型建模，估算出場景透射率，優化處理粗略透射率圖后，得到增強的紅外圖像。

但是上述傳統方法均因缺乏色彩通道處理過程，導致分形圖像細節增強效果不理想。因此，本文以牛頓迭代法為算法依據，提出一種新的分形圖像紋理細節增強方法。考慮最大直徑與序列塊規格參數，提升分形維數精確度與紋理重構質量；通過增強較大的序列塊紋理邊緣，增加待增強部分的圖像信息覆蓋率，防止紋理結構遭到破壞；減小序列塊規格，提高紋理處理精細度。

2 分形圖像繪制

2.1 基于牛頓迭代算法的分形圖像迭代初始點設置

采用牛頓迭代算法計算復平面函數f(Z)=0，該函數的牛頓迭代方程表達式如下所示

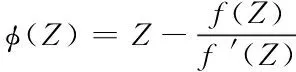
(1)

(2)

f(Z)零點為φ的超吸引不動點，當|Z|為較大值時，得出下列表達式

(3)

式中，f(Z)的階是n，斥性點是∞，因此可得出下列表達式

A(ω)={Z0：φ(Zk)→ω}

(4)

式中，零點ω吸引域為A(ω)，也就是基于牛頓迭代算法收斂于零點ω的初始點集合。

利用牛頓迭代算法繪制分形圖像，設定迭代方程，選取復平面上任意一點Z0為迭代初始點，通過著色處理形成分形圖像。假設A×B點是顯示器分辨率，顏色的可顯示種數為k+1，其中，k=0，1，2，…，具體流程描述如下：

1)計算n在迭代公式f(Z)=zn-1內的取值范圍；

2)選取分形圖像繪制的坐標范圍極值xmax、xmin、ymax與ymin，假設M為當前的迭代次數，N為迭代最大次數，ε是迭代精度，則分別得到下列X、Y方向上的坐標差值占比計算公式

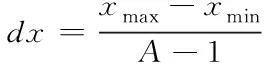
(5)

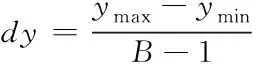
(6)

3)采用下列公式設置迭代初始點值

Z0=x0+y0i

(7)

其中，i為常數，X、Y方向上的初始點值為x0與y0，表達式分別如下

x0=xmin+mx×dx

(8)

y0=ymin+my×dy

(9)

式中，mx與my表示X、Y方向的可用像素個數，取值范圍分別是mx=0，1，…，A-1、my=0，1，…，B-1。

2.2 零點吸引域映射

根據上節內容利用牛頓迭代算法計算f(Z)=Z3-1=0的解值，由式(1)推導出下列迭代函數方程式

(10)

假定圖像繞原點轉動120°的旋轉變換為ρ(Z)=Ze2πi/3，代入式(10)可得出下列表達式

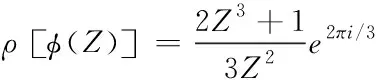
(11)

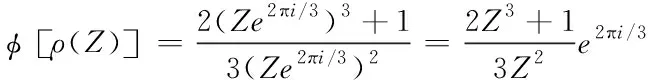
(12)

將上列兩式結合比較后，推導出下列等式關系

ρ[φ(Z)]=φ[ρ(Z)]

(13)

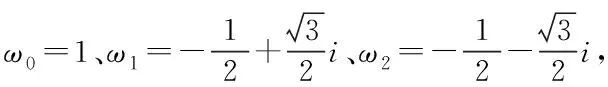
3 分形圖像紋理細節增強方法

3.1 分形圖像色彩通道架構

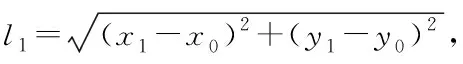
3.2 基于分形維數與序列塊的細節增強

分形的主要特征與度量形式是分形維數[7]，用于描述穩定特征量。假設分形圖像序列塊Rn的一個非空有界集合為F，最大直徑是ε且能夠涵蓋非空有界集合F的集合最小數量為Nε(F)，則采用下列公式描述非空有界集合F的分形維數

(14)

針對分形圖像的分形維數，把圖像劃分成網格，邊長是ε，并求取涵蓋圖像目標部分的網格數量Nε(F)，若單個像素點尺度ε為一個二維集合，不存在分形屬性，圖像序列塊R是單個像素，此時，都無法增強分形圖像的紋理細節，所以，當圖像序列塊R超出2個像素時，將分形圖像看成拓撲維數取值非整數圖像，經計算圖像的分形維數，完成目標圖像分類，若分形維數接近，則圖像屬于同類圖像，圖像之間的相似度隨著維數差異的變小而升高。

由于分形圖像的對數形式與分形維數不存在相關性，故利用下列計算公式求解分形圖像的分形維數：

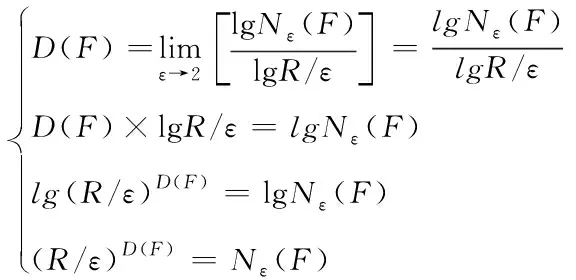
(15)

當分形圖像屬于同一幅時，ε1<ε2，可通過下式推導出與之對應的分形維數Dε1(F)與Dε2(F)的關系：

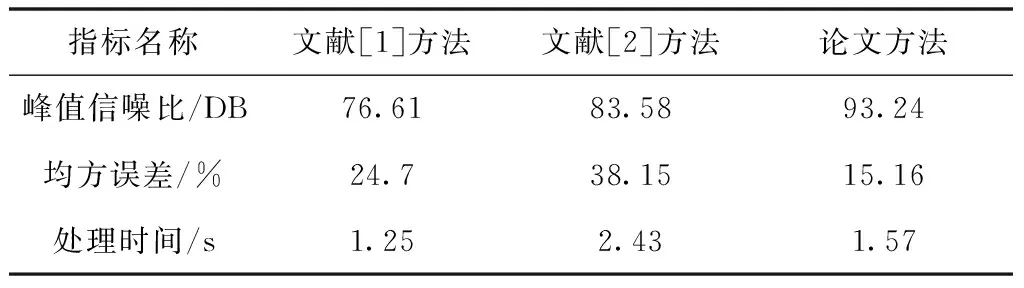
?Dε1(F)

(16)

當分形圖像屬于同一幅時，R1

R1

(17)

通過上列兩式可以發現，最大直徑ε取值越小，分形維數精確度越高，分形圖像紋理重構質量隨著序列塊R規格的減小而增加。分形圖像的紋理粗糙度與模式復雜性信息特征，均能夠從非線性[8]角度利用分形維數來描述。增強分形圖像紋理細節時，通過增強較大的序列塊紋理邊緣，使重構的待增強部分覆蓋更多的圖像總體信息，基于圖像整體框架，防止紋理結構遭到破壞，不斷減小序列塊規格，細化紋理增強效果。

當分形圖形內的相似子塊在鄰域位置出現時，部分子塊將產生不完全匹配現象，所以，為進一步提升紋理細節增強效果，應用局部迭代策略來解決此類問題。

若序列塊Ri與待增強部分G相交，則搜索主塊Di也與區域G相交。選取對應于各序列塊Ri的主塊Di，計算收縮仿射變換[9]wi，根據wi(Di)=Ri得出下列關系式

wi(Di∩G)≈Ri∩G

(18)

假定完備的度量空間為(X，d)，X所有非空集子集架構的空間為Γ(X)，若x∈X，集合J∈Γ(X)，則點x到集合J的距離用d(x，J)=min{d(x，y)，y∈J}表示；若集合J，Q∈Γ(X)，則集合J∈Γ(X)與集合Q∈Γ(X)的距離用d(J，Q)表示；采用下列等式描述Γ(X)內點j與點q間的Hausdorff距離[10-11]

h(j，q)=d(j，q)∨d(q，j)

(19)

4 實驗結果與分析

實驗的運行環境采用Windows 10操作系統，酷睿i5-4580 3.3GHz處理器，圖像部分由MATLAB軟件實現。

從某個分形圖像數據庫中，任意選取兩幅分形圖像作為實驗對象(如圖1所示的實驗樣本)，分別采用文獻[1]提出的基于結構層與紋理層分離的圖像增強方法與文獻[2]提出的基于簡化大氣散射模型的單幅紅外圖像增強方法以及論文方法增強所選圖像的紋理細節，對比各方法的仿真結果，得出實驗結論。為驗證方法的適用性與有效性，再選用一幅細節豐富的分形圖像用于探索增強效果(如圖2所示)。

圖1 實驗樣本分形圖像示意圖

4.1 不同參數指標對增強效果的影響測試

由于迭代初始參數M、色彩初始值(C1，C2，C3)為圖像紋理細節的主要影響因素，下面分別探討各因素對增強效果的影響。

1)設定其它參數相同，迭代初始參數M取不同值時：假設色彩初始值RGB是(118，158，108)，色彩漸變參數a=5，迭代初始參數N=24，色彩通道表達式與圖1一致，M取值11與12時的分形圖像分別如圖2所示。

圖2 不同迭代初始參數M的分形圖像增強效果

2)設定其它參數相同，色彩初始值取不同值時：假設色彩漸變參數a=6，迭代初始參數M=10，N=24，色彩通道表達式與圖1一致，色彩初始值RGB取(118，158，108)與(100，210，140)時的分形圖像分別如圖3所示。

圖3 不同色彩初始值的分形圖像增強效果

根據圖2、圖3的實驗結果可知，本文給出的影響分形圖像細節增強的理論是可靠的，實驗中以迭代初始參數和色彩初始為例，對實驗樣本進行細節增強處理，參數變化情況下，所得到的增強效果是不同的。

4.2 各方法增強效果對比

為進一步驗證所提方法的應用有效性，利用PSNR(Peak Signal-to-Noise Ratio，峰值信噪比)、MSE(Mean Square Error，均方誤差)以及處理時間三個指標作為測試指標，采用文獻[1]方法、文獻[1]方法作為對照方法，利用幾種方法分別進行分形圖像的細節增強，各方法的指標數值如表1所示。

表1 各方法評價指標值

根據表1中數據可以看出，相比文獻[1]與文獻[2]方法，論文方法通過分形維數與序列塊的粗略增強形式與解得的壓縮映射吸引子唯一解，得到了最優的峰值信噪比與均方誤差，因運算量較大，所以處理時間不是最理想狀態，運算速度僅低于文獻[2]方法。

5 結論

根據牛頓迭代算法原理與分形理論的契合性，本文設計基于牛頓迭代算法的分形圖像的紋理細節增強方法，由于研究方向與水平深度存在的局限性，應在以下方面做出改進：在保持紋理細節精度的基礎上，提出一種運算方法，簡化計算量，提升運行速率，加快圖像處理速度；本文應用算法相對比較單一，應在今后的研究中引入其它有效的增強算法加以混合，提高方法的綜合性能，令該方法具有更廣泛的應用前景。