基于灰度梯度正則化的數(shù)字圖像位移標(biāo)定仿真

鄧秋菊，徐 琴，王 寧

(重慶郵電大學(xué)移通學(xué)院，重慶 401520)

1 引言

標(biāo)定技術(shù)存在一定限制性，且容易受到周圍環(huán)境影響，導(dǎo)致標(biāo)定結(jié)果通常存有誤差，影響數(shù)字圖像內(nèi)容識別的準(zhǔn)確性。數(shù)字圖像位移是圖像內(nèi)容識別的重要檢測內(nèi)容，位移標(biāo)定以固定基準(zhǔn)點為參照，采用相應(yīng)的傳感器，標(biāo)定數(shù)字圖像移動點相對于固定基準(zhǔn)點的位移變化[1]。

文獻[2]提出基于遺傳算法的數(shù)字圖像位移標(biāo)定方法。該方法通過與之相關(guān)系數(shù)可實現(xiàn)對圖像匹配程度進行衡量，將歸一化函數(shù)視為相關(guān)參數(shù)和該方法的最終目的函數(shù)，對目的函數(shù)進行求解，可得到圖像的位移，并對其進行標(biāo)定。但該方法的標(biāo)定精度較低，應(yīng)用效果較差；文獻[3]提出基于Tsai算法的圖像位移標(biāo)定方法。運用了攝像機鏡頭畸變模型，對成像設(shè)備的檢測系統(tǒng)進行成像誤差進行計算，同時設(shè)計出了點陣式標(biāo)定模板，對圖像位移進行標(biāo)定。但該方法過于簡單，標(biāo)定范圍有限，不適用于所有圖像位移的標(biāo)定；文獻[4]提出基于單個讀數(shù)頭檢測方法的圖像位移標(biāo)定。采用傅里葉逼近模型對讀數(shù)頭存在的誤差進行拆分，得到多次諧波的疊加，并利用檢測值差商對誤差進行估算，將差商階數(shù)增大，以降低逼近模型的誤差，并采用最小二乘法對標(biāo)定參數(shù)進行優(yōu)化，最后采用優(yōu)化后的標(biāo)定模型對圖像位移進行標(biāo)定。但該方法的穩(wěn)定性較差，且耗費成本較高。

上述方法在標(biāo)定圖像位移時，需要采用極高精準(zhǔn)度的檢測設(shè)備，導(dǎo)致成本較高，且在檢測和標(biāo)定的過程中，易受環(huán)境等影響，使最終結(jié)果帶來噪聲干擾的結(jié)果。為此，提出基于灰度梯度正則化的數(shù)字圖像位移標(biāo)定方法。經(jīng)過仿真驗證，本文方法具有較高的標(biāo)定精度，且檢測所用儀器設(shè)備簡潔，成本較低。

2 數(shù)字圖像位移標(biāo)定方法

2.1 去噪處理

由于拍攝成像時，會受到周圍環(huán)境的影響和相機鏡頭的誤差，導(dǎo)致圖像成像存在誤差。為了消除誤差，需要采取圖像去噪的方法處理圖像，同時還要標(biāo)定相機。

為了避免檢測結(jié)果存在噪聲干擾現(xiàn)象，提出基于灰度梯度正則化的圖像去噪方法[5]。該方法在以函數(shù)存在誤差為δ的情況下，創(chuàng)建泛函令目標(biāo)函數(shù)的誤差降到最小，提高灰度梯度正則化的抗噪能力。

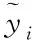
(1)

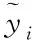
根據(jù)灰度梯度正則化方法求得的正則解f*是一個三系樣條函數(shù)，包括誤差水平參數(shù)δ，該函數(shù)的具體表達形式為

f*=aj+bj(x-xj)+cj(x-xj)2+dj(x-xj)3

x∈[xj，xj+1]，j=0，1，…，n-1

(2)

式中：aj、bj、cj、dj分別表示需要求解的函數(shù)系數(shù)。

該函數(shù)的系數(shù)可以滿足以下約束條件

(3)

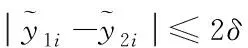
(4)

則誤差水平參數(shù)δ的具體表達式為

(5)

通過獲取誤差水平參數(shù)，實現(xiàn)了對正則化參數(shù)的求解，從而完成圖像的去噪處理。

2.2 圖像測點位移計算

為了減少標(biāo)定存在的誤差，以及消除相機鏡頭的畸變問題，在傳統(tǒng)數(shù)字圖像相關(guān)技術(shù)上，引入位移標(biāo)定方法，完成攝像機的標(biāo)定，進而實現(xiàn)對圖像測點位移的標(biāo)定[6]。

在圖1中，假設(shè)空間某點P在世界坐標(biāo)系O-XwYwZw中的坐標(biāo)表示為(Xw，Yw，Zw)T，在攝像機坐標(biāo)系o-xyz中的坐標(biāo)表示為(x，y，z)T。(X，Y，1)T和(u，v，1)T之間的關(guān)系為

(6)

式中：dX表示像素在X軸上的距離，dY表示像素在Y軸上的距離，這兩個參數(shù)為固定存在的參數(shù)，(u0，v0)T表示主點坐標(biāo)。

攝像機坐標(biāo)系坐標(biāo)(x，y，z)T和坐標(biāo)(X，Y，1)T之間的關(guān)系可用下式進行表示

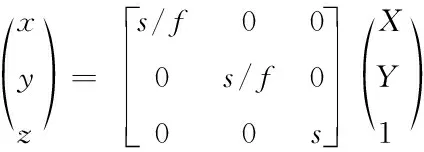
(7)

式中：f表示為攝像機焦距，s表示比例系數(shù)。

(Xw，Yw，Zw)T和(x，y，z)T之間的關(guān)系為

(8)

式中：R表示坐標(biāo)旋轉(zhuǎn)矩陣，T表示由攝像機坐標(biāo)系變換到世界坐標(biāo)系的水平方向位移向量。可通過具體標(biāo)定方法對這兩個參數(shù)進行計算。

將式(6)代入到式(7)并整理，可得到

(9)

將式(8)和式(9)進行聯(lián)立，可通過坐標(biāo)(u，v，1)T對(Xw，Yw，Zw)T點在世界坐標(biāo)系中的坐標(biāo)f*進行計算。

計算比例系數(shù)s[7]。該值與世界坐標(biāo)系的選擇有關(guān)，將世界坐標(biāo)系創(chuàng)建在被檢測的相機上，世界坐標(biāo)系的XWYW平面和圖像測點發(fā)生位移的平面重合，ZW軸可滿足右手坐標(biāo)系。在坐標(biāo)系中隨機選擇三點確定的平面，該平面的表達方程為

Ax+By+Cz+D=0

(10)

將式(9)轉(zhuǎn)換成方程組的形式，可得出

(11)

將式(11)代入到式(10)中，并進行整理，可得到比例系數(shù)s的計算公式為

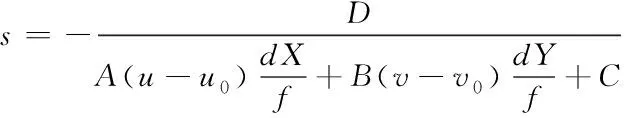
(12)

通過在圖像上的坐標(biāo)(u，v，1)T就可計算出世界坐標(biāo)系中的坐標(biāo)(Xw，Yw，Zw)T。

2.3 相機標(biāo)定計算

為了避免圖像位移發(fā)生較大的變化，因此需要進行圖像位移標(biāo)定，最好的方法就是對相機進行標(biāo)定，只有相機配置和穩(wěn)定性保證了，才能保證圖像位移的穩(wěn)定性[8-9]。

對相機標(biāo)定時以圖像位移標(biāo)定的基礎(chǔ)，作為數(shù)字圖像信息獲取的核心步驟，在標(biāo)定的過程中，由于相機鏡頭生產(chǎn)和加工的過程中會出現(xiàn)誤差的現(xiàn)象，如圖1所示。

圖1 相機誤差示意圖

為消除相機鏡頭存在的畸變現(xiàn)象，提出針對平面靶標(biāo)的標(biāo)定方法。該方法是一個非線性模型相機的線性標(biāo)定方法，只需要考慮到二階鏡像畸變，畸變模型的具體表達式可用下式進行表示

(13)

1)對單應(yīng)性矩陣進行求解

(14)

式中：A表示相機中各項參數(shù)，具有含有

(15)

式中：α表示u軸的尺度因子，β表示v軸的尺度因子；γ表示u軸和v軸的水平因子。

將式(14)進行進一步變換，得出下式形式

(16)

式中：ri表示旋轉(zhuǎn)矩陣R的第i列。

通過上述變換，屆時標(biāo)定板平面上的點M和相應(yīng)的像素點m之間含有一個變換矩陣，也就是單應(yīng)性矩陣H，具體為

(17)

其中

(18)

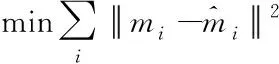
(19)

2)相機內(nèi)部各項參數(shù)進行求解

對單應(yīng)性矩陣H進行求解后，可得出

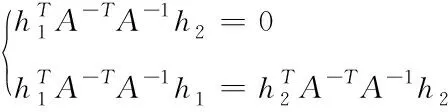
(20)

令

(21)

則

(22)

其中

(23)

將式(20)進行改編，得出

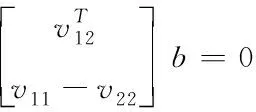
(24)

對標(biāo)定板拍攝了n個圖像，將其轉(zhuǎn)換為方程，并組疊起來，得出Vb=0。當(dāng)對b求解后，可求出矩陣A，上述計算結(jié)果均為初始值，進行優(yōu)化搜索，進而可對相機內(nèi)部各項參數(shù)的準(zhǔn)確值進行計算。通常采集10幅以內(nèi)圖像就可以獲取到較好的標(biāo)定結(jié)果。

3 仿真證明

實驗設(shè)備為某公司生產(chǎn)的相機，采用頻率可達到55Hz，傳感器采用KODAK CCD，相加分辨率為1000(H)*1000(V)，像素為8.2μm*8.2μm。光學(xué)鏡頭為15～39mm的變焦鏡頭。

圖2 實驗圖像標(biāo)定設(shè)備

實驗在配置為：CPU Intel 酷睿i5 4590 3.5Hz，主板 華碩B85M-F，內(nèi)存 金士頓駭客神條FURY 8GB DDR3 1866，硬盤希捷Barracuda 1TB 7200轉(zhuǎn) 64MB 單碟(ST1000DM003)，操作系統(tǒng) Windows 7旗艦版的計算機上創(chuàng)建仿真平臺。以該平臺為背景，對以下兩幅樣本圖像進行處理。

圖3 實驗樣本圖像

圖4 樣本一圖像位移標(biāo)定結(jié)果

圖5 樣本二圖像位移標(biāo)定結(jié)果

根據(jù)以上圖像標(biāo)定結(jié)果可知，對于兩幅樣本圖像，其主要標(biāo)記點數(shù)量是不同的，密集程度也是不同的，利用不同方法對其標(biāo)定時，會更好的驗證方法的有效性。針對于文獻[3]方法，其標(biāo)定結(jié)果雖然并無錯誤，但是標(biāo)記特征信息明顯是不完整的，當(dāng)出現(xiàn)多個特征需要被標(biāo)定時，該方法無法實現(xiàn)同時完成標(biāo)定動作，這說明傳統(tǒng)方法無法滿足目前的圖像標(biāo)定技術(shù)要求。而研究方法在標(biāo)定結(jié)果上看是更具優(yōu)勢的，不僅可以完成標(biāo)定圖像，并且其標(biāo)記對象規(guī)劃更為清晰，大大提升該方法的應(yīng)用性能。

圖6 標(biāo)定精度對比

在圖像標(biāo)定結(jié)果的基礎(chǔ)上，利用仿真平臺輸出不同方法的標(biāo)定精度，并將數(shù)據(jù)整理成圖5折線圖。從圖中各個方法的標(biāo)定精度變化走勢來看，隨著實驗次數(shù)的增多，標(biāo)定精度會降低，這是因為實驗次數(shù)越多，方法所處理的圖像數(shù)量就越多，所以精度出現(xiàn)下降是不可避免的，但是在此情況下，研究方法的精度始終較高，這說明研究方法是符合實際應(yīng)用要求的。

為了進一步驗證本文方法的有效性，將均值誤差和標(biāo)準(zhǔn)差作為本次實驗的評價指標(biāo)，將本文方法的實驗結(jié)果與其它兩種方法進行對比，具體實驗結(jié)果如圖7所示：

通過分析圖7(a)得出：圖7(a)是三種方法的均值誤差對比結(jié)果，根據(jù)圖(a)可知，三種方法中基于遺傳算法的數(shù)字圖像標(biāo)定方法和Tsai標(biāo)定方法的均值誤差變化趨勢較大，其中基于遺傳算法的數(shù)字圖像標(biāo)定方法的均值誤差最大值幾乎接近0.015，最小值也超過-0.010，誤差是三種方法中最大的，而Tsai標(biāo)定方法的均值誤差相對遺傳算法要好一些；本文方法的均值誤差變化不是很大，上下波動的范圍都在-0.005～0.005之間，說明本文方法的均值誤差較小，標(biāo)定結(jié)果較準(zhǔn)確。

通過分析圖7(b)得出：圖7(b)是三種方法的表差對比結(jié)果，由圖可直接看出，Tsai標(biāo)定方法的標(biāo)準(zhǔn)差最大值幾乎接近0.045，基于遺傳算法的數(shù)字圖像標(biāo)定方法的標(biāo)準(zhǔn)差最大值也已經(jīng)超過0.030，而本文方法的標(biāo)準(zhǔn)差是三種方法中最小的，最大值沒有超過0.015，再次驗證本文方法的準(zhǔn)確性。

4 結(jié)束語

傳統(tǒng)方法標(biāo)定的數(shù)字圖像位移，由于沒有考慮到成像過程中，存在環(huán)境等因素的干擾和成像設(shè)備的鏡頭問題，導(dǎo)致標(biāo)定結(jié)果存在較大誤差。為此提出基于灰度梯度正則化的數(shù)字圖像位移標(biāo)定方法。該方法通過對兩種影響因素進行優(yōu)化，彌補了傳統(tǒng)方法的不足之處。采用灰度梯度正則化方法將圖像存在的噪聲等干擾進行消除，同時對相機的鏡頭畸變進行計算并標(biāo)定，進而實現(xiàn)對圖像測點位移的標(biāo)定。經(jīng)過仿真證明，本文方法具有較高的標(biāo)定準(zhǔn)確度，且可快速地實現(xiàn)對目標(biāo)的標(biāo)定。