基于自適應伸縮因子的變論域模糊PID 振動控制方法

蔣 偉，劉 綱,2，王 濤，高 凱

(1. 重慶大學土木工程學院，重慶 400045；2. 山地城鎮建設與新技術教育部重點實驗室，重慶 400030)

隨著土木工程結構向高、大、長方向發展，結構的非線性、復雜構造等影響益發顯著[1]，傳統抗震設計已無法有效解決結構過大振動問題，故振動控制已成為土木工程領域的重要研究分支。按是否需要外加能源、結構自身響應信息等，振動控制可分為被動、主動、半主動和混合控制4 類[2]。國內外大量學者針對以上四種控制方法進行了深入研究，取得了豐碩成果。其中，半主動控制根據結構響應信息實時改變結構的動力特性(剛度、阻尼)，具有耗能小、穩定性高及動力可調等優點，已成為振動控制領域的前沿研究方向。

目前，國內外已成功研發了變阻尼、變剛度和變剛度變阻尼等多種半主動控制系統[3]，并在控制裝置與控制算法2 個方面取得了長足進步。在控制裝置方面，近年來國內外學者和工程界研制了可變剛度、阻尼的阻尼器、隔震支座等控制裝置，特別是隨著磁流變(magneto-rheological，MR)、記憶合金等智能材料的興起，變阻尼控制裝置得到了飛速發展，研制了粘滯變阻尼器、磁流變阻尼器、電流變阻尼器及壓電變摩擦阻尼器等多種新型變阻尼控制裝置[4]，已在實驗室結構、實際工程結構中發揮了重要作用。

在變阻尼系統的控制算法方面，19 世紀初即提出了線性二次狀態調節器(linear quadratic regulator，LQR)、滑動模態及Bang-Bang 等控制算法[4]。針對磁流變、電流變等新型阻尼器，逐步提出了線性二次型最優控制[5]、H∞控制[6]等方法。例如，Dyke 等[7]結合線性二次高斯(linear quadratic Gaussian， LQG)與限幅最優控制算法，發展了一種基于加速度反饋的限幅最優控制策略；王梁坤等[8]結合Hilbert-Huang 變換理論和LQG 算法，構建了一種能實時調節電渦流單擺式調諧質量阻尼器擺長和阻尼系數的半主動控制方法；潘兆東等[9]提出了一種基于輸出反饋的H∞保性能魯棒分散控制算法，12 層框架結構數值模擬結果表明所提方法在各層層間位移峰值與絕對加速度上的控制效果均優于傳統LQG 集中控制算法；王慧萍等[10]建立了一種基于可變摩擦阻尼力的斜拉索半主動控制算法，實現了斜拉索的多模態同步控制。

針對LQG、LQR 等控制方法需要結構精確數學模型的難題，業界發展了智能控制方法，例如郭佳等[11]引入模糊控制算法，20 層框架結構數值模擬結果表明所提算法對層間位移和樓層速度的減震率均高達60%左右；潘兆東等[12]提出了一種自適應學習率徑向基(radial basis function，RBF)神經網絡滑模分散控制算法，9 層鋼結構Benchmark模型數值模擬結果表明所提方法的首層位移響應峰值控制率明顯優于集中控制；Kim 等[13]利用模糊控制理論計算MR 阻尼器所需控制力，較好控制了橋梁結構在風、雨共同作用下的共振現象；馬涌泉等[14]結合變論域模糊控制(variable universe fuzzy pid，VUFP)與剪切最優半主動控制，提出了變論域自適應模糊分散控制方法，數值模擬結果表明所提方法的減震效果較VUFP 方法更優；寧響亮等[15]將VUFP 控制算法用于公路橋梁的非線性振動控制，仿真結果表明在控制力峰值相等情況下，VUFP 算法的控制效果明顯優于傳統模糊和LQG 控制算法；許睿等[16]提出了針對大型薄膜結構的VUFP 方法，仿真結果表明該方法能顯著提升模糊控制器對結構振動幅值的魯棒性。

傳統VUFP 算法均采用函數模型來設計伸縮因 子(contracting expanding factors， CEFs)， 但CEFs 的參數往往由專家經驗確定[17]，有時難以實現結構最優控制。為解決該問題，Cui 等[18]引入不規則隸屬函數和模糊推理來在線估計CEFs 參數，提高了系統控制性能。但繁瑣的積分運算使該方法無法適用于實際工程結構。之后，Gong 等[19]提出了一種用加權和策略來代替CEFs 中積分運算的方法。但該方法無法保證控制系統的穩定性。近年來，隨著人工智能算法的發展，神經網絡[20]、蟻群算法[21]等逐漸被用于優化CEFs 的參數，但在復雜控制系統中，此類方法的在線計算成本很高，易導致嚴重的時滯現象。因此，如何優化CEFs 參數成為VUFP 控制方法中的一個重要的研究課題。

鑒于模糊控制方法的潛在優勢，本文基于傳統VUFP 控制算法，采用半主動控制系統誤差及誤差變化率設計了一種新型函數型伸縮因子，實現了伸縮因子參數的自適應調整；然后，基于穩定性理論，從理論上驗證了所提伸縮因子的合理性，解決了伸縮因子缺乏模糊規則導致控制系統性能降低的難題，從而建立考慮伸縮因子自適應改變的變論域模糊PID(NEVUFP)振動控制方法。最后，利用數值模擬與實驗結構模型對所提方法的有效性進行驗證。

1 變論域模糊PID 控制

設被控系統在第t時刻的目標響應為y(t)、實際響應為r(t)，兩者之差為誤差信息e(t)，即e(t)=r(t)-y(t)。半主動控制算法的基本思路是根據誤差信息及外部激勵信息計算被控系統所需實時控制參數(例如剛度、阻尼等)，并結合執行機構實現被控系統參數的及時調整，從而實現最優振動控制。

PID 算法通過對誤差信息e(t)的比例、積分和微分的線性組合[22]，得到結構振動控制所需參數u(t)：

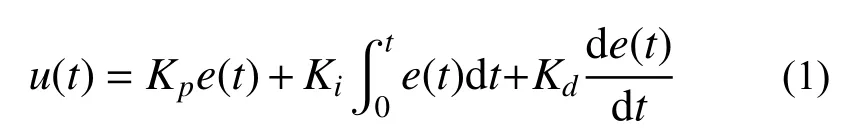
其中，Kp、Ki和Kd分別為比例、積分和微分系數，往往在綜合考慮系統誤差、響應時間及穩定性的基礎上，通過專家經驗確定。

大量算例和實驗表明，采用固定Kp、Ki和Kd系數取得的控制效果差強人意[23]。針對這一問題，根據e(t)及其導數ec(t) (ec(t)=de(t)/dt)的變化，模糊PID 算法[24]基于模糊理論，動態改變Kp、Ki和Kd系數。具體而言，首先將e(t)和ec(t)作為模糊控制器的輸入變量xi(t) (i=1,2，且x1(t)=e(t),x2(t)=ec(t))；將ΔKp(t)、ΔKi(t)和ΔKd(t)作為模糊控制器的輸出變量yj(t) (j=1,2,3 且y1(t)=ΔKp(t),y2(t)=ΔKi(t),y3(t)= ΔKd(t))；并分別設初始論域為Xi=[-Ei,Ei]、Yj=[-Uj,Uj]，其中，Ei、Uj為論域邊界。將輸入、輸出變量的論域均劃分為7 個模糊子集：NB(正大)、NM(正中)、NS(正小)、ZV(零)、PS(負小)、PM(負中)、PB(負大)，并確定隸屬度函數的形式(常用類型有三角形、梯形、鐘形等)，如圖1(a)所示；然后，經輸入模糊化、模糊推理及解模糊化3 個過程得到輸出變量ΔKp(t)、ΔKi(t)和ΔKd(t)的大小，從而在線調整比例、積分和微分系數：

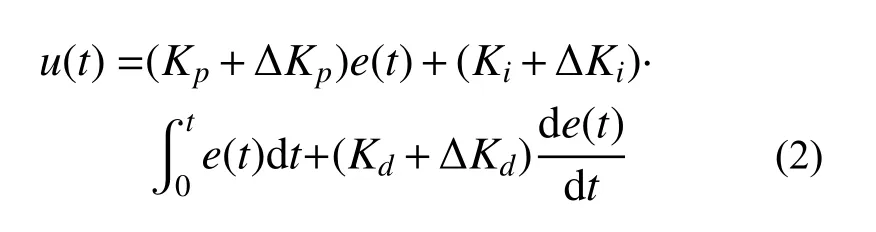
當模糊PID 算法中論域大小選擇不當時，較難保證模糊控制器的控制效果。針對這一問題，文獻[25]提出了變論域模糊PID(VUFP)算法，即通過引入伸縮因子來在線調整模糊控制器中輸入、輸出變量的論域范圍：根據e(t)和ec(t)計算伸縮因子α(e(t))、α(ec(t))和β(e(t),ec(t))，其中：α(e(t))、α(ec(t))分別為輸入變量e(t)、ec(t)的伸縮因子；β(e(t)，ec(t))為三個輸出變量ΔKp(t)、ΔKi(t)、ΔKd(t)共同的伸縮因子。然后，對輸入、輸出變量的初始論域進行伸縮調節，以第i個輸入變量為例，調節后得到新論域([-α(xi(t))Ei, α(xi(t))Ei])，如圖1(b)、圖1(c)所示。

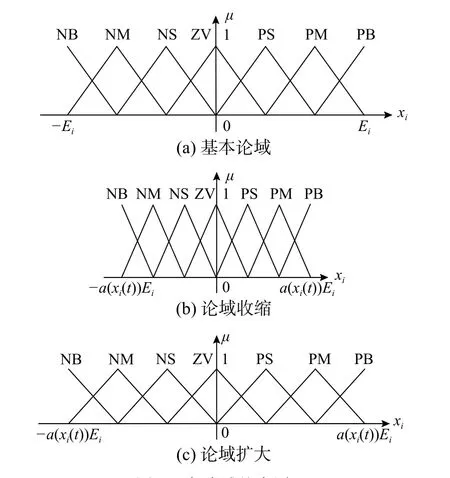
圖1 變論域基本原理Fig. 1 The basic principles of variable universe

限于篇幅，本文僅給出了α(e(t))、α(ec(t))的部分模糊控制規則，具體設計細節詳見文獻[26]：

1) 當e(t)或ec(t)增大時，為保證控制系統始終處于可控范圍內， α(e(t)) 或 α(ec(t))應保持不變，因此論域范圍也保持不變；

2) 當e(t)或ec(t)減小時，為確保控制器能實施高效控制， α(e(t)) 或 α(ec(t))應足夠小(盡量接近0)，因此論域范圍被壓縮。

綜合考慮上述設計原則后， α(e(t)) 、α(ec(t))模糊控制規則的設計如表1 所示。其中，B 表示較大，M 表示中等，S 表示較小，Z 表示0。

表1 α(e(t)) 、 α(ec(t))的模糊控制規則Table 1 The fuzzy control rules of α(e(t)) andα(ec(t))

但在實際控制過程中，由于控制系統非線性、時滯性等因素的影響，無法對任意伸縮因子建立如表1 所示完善的模糊控制規則。基于函數模型的方法直接采用某些特殊函數設計伸縮因子，避免了基于模糊規則的方法在缺乏完善模糊規則導致控制性能降低的問題，因此本文針對基于函數模型的VUFP 算法進行研究。在工程應用中，目前通常選用比例指數函數模型設計伸縮因子[27]：

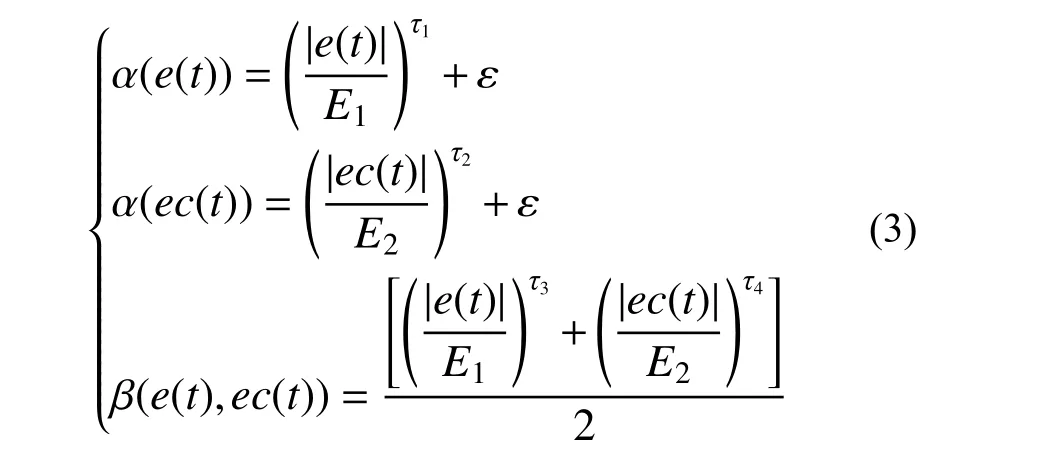
式中：ε 為一充分小的正數；E1、E2分別為輸入變量e(t)、ec(t)的初始論域邊界；τi(i=1,2,3,4)為伸縮因子設計參數，且τi∈[0,1]。

VUFP 算法的具體計算流程如圖2 所示。

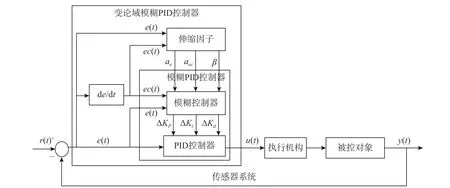
圖2 VUFP 控制系統流程圖Fig. 2 The flowchart of VUFP control system

2 基于伸縮因子參數自適應的VUPF控制算法

2.1 新型伸縮因子設計

應指出的是，函數型伸縮因子中τi是人為選定的常數，缺乏明確物理意義。盡管相關學者針對τi進行了大量研究，給出了大致取值范圍，但每個大型土木工程結構不盡相同，無法給出具有普遍意義的選值方法。因此，本文提出根據系統誤差及誤差變化率實時調整τi：

式中，δ 為足夠小的正數，以使分母不為零。當τ1＞1 時，取τ1=1。為保持輸入、輸出變量的協調性，取τ2=τ3=τ4=τ1。將式(4)代入式(3)，則得到新型函數型伸縮因子為：

2.2 新型伸縮因子穩定性分析

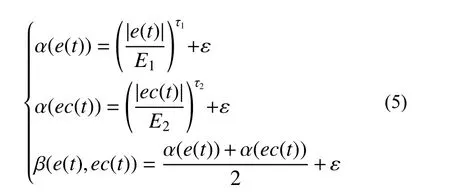
伸縮因子應具有穩定性，才能保證控制系統能快速降低e(t)和ec(t)，從而使結構趨于穩定[28]。以下分別從對偶性、避零性、單調性、協調性和正規性5 個方面驗證新型伸縮因子的穩定性。

1) 對偶性

5) 協調性

將式(5)改寫成 |e(t)|關 于 α (e(t))的函數：

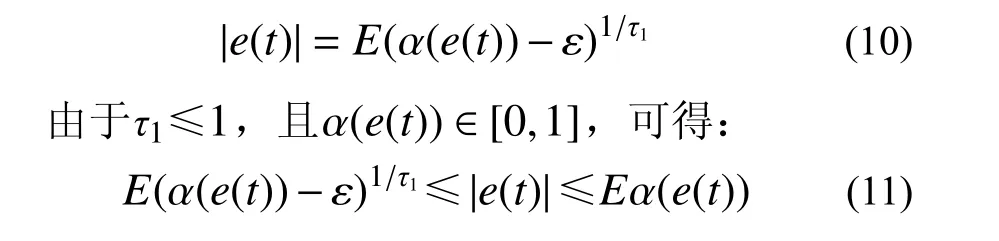
因此 |e(t)|≤Eα(e(t))，滿足協調性關系，保證調整后論域不會超出初始論域([-E1,E1])范圍。同理可證， α (ec(t))也滿足協調性。

在 式(5)中， β(e(t),ec(t)) 是α(e(t))、α(ec(t))的線性組合，易證 β(e(t),ec(t))也滿足上述5 個條件。綜上所述，本文提出的新型伸縮因子α(e(t))、α(ec(t)) 、β(e(t),ec(t))均滿足上述五種穩定性條件。

將本節提出的新型伸縮因子與傳統VUFP 算法相結合，建立基于自適應伸縮因子的變論域模糊PID(NEVUFP)控制方法，具體流程如圖3 所示。圖中加底色部分表示本文中新增的自適應函數。

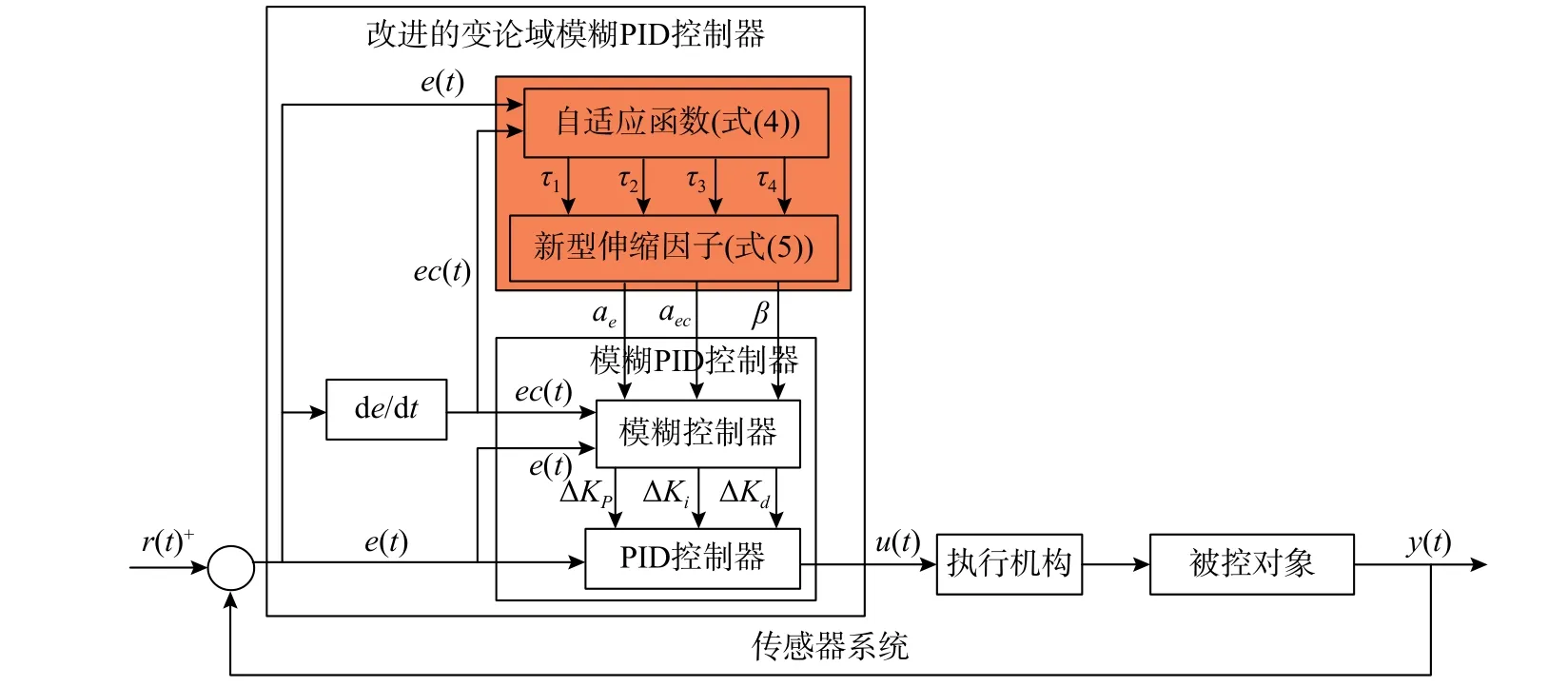
圖3 NEVUFP 控制系統流程圖Fig. 3 The flowchart of NEVUFP control system

3 數值模擬

3.1 三層框架模型

建立3 層平面框架結構模型，假設樓層質量均集中在樓板，各層質量均為98.3 kg、剛度均為6.84×105N·m-1，第1 層阻尼為125 N·s·m-1，第2 層～3 層阻尼均為50 N·s·m-1，結構底部與基礎剛接。采用Simulink 模擬該框架結構半主動控制系統，包括結構響應信息采集、控制器以及設置于結構底層的磁流變(MR)阻尼器，如圖4 所示。

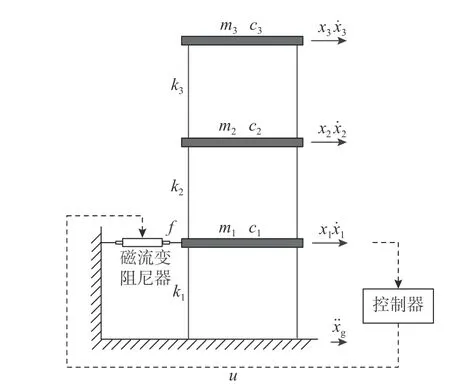
圖4 三層框架結構Fig. 4 Three-storey frame structure

磁流變阻尼器力學性能選用現象模型來模擬[29]，如圖5 所示。

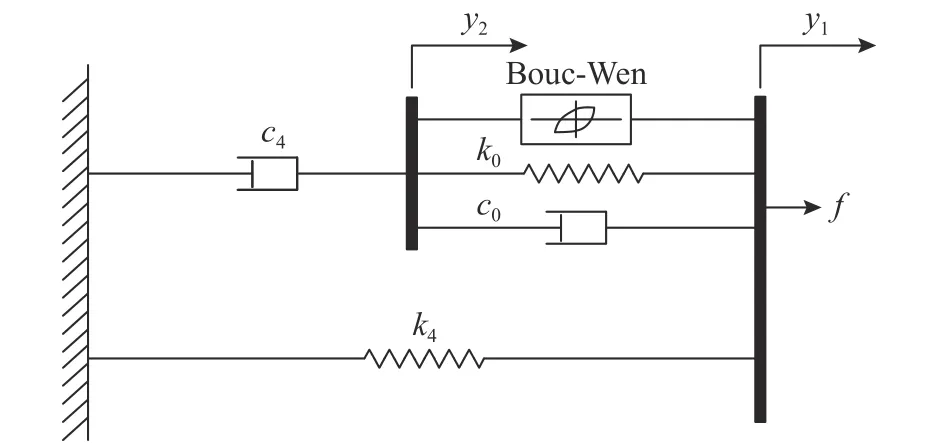
圖5 MR 阻尼器現象模型Fig. 5 The phenomenological model of MR damper

現象模型阻尼力f可表示為：

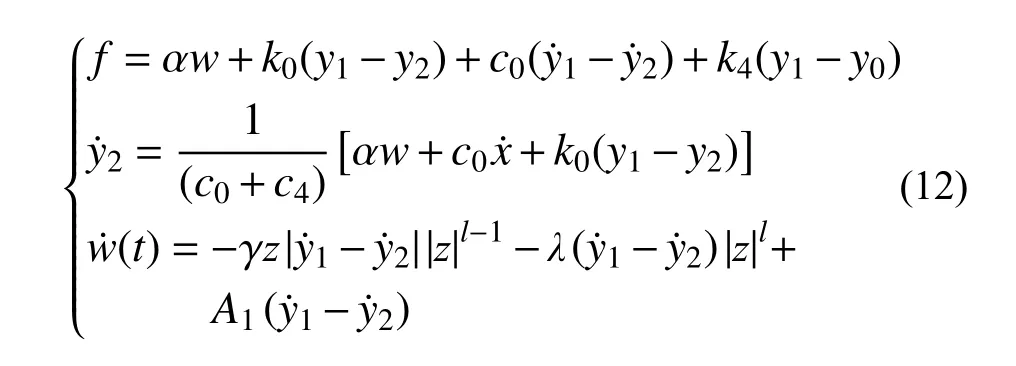
式中：k4為儲能器剛度；c0、c4分別為較大、較小速度下阻尼器的等效阻尼系數；y0為儲能器初始位移；k0為較大速度下阻尼器的等效剛度；y1為阻尼器位移；y2為彈簧k0左端位移；γ、λ、l和A1為阻尼器相關調節參數，根據磁流變液特性和磁流變阻尼器的結構特性進行取值；w為中間變量。

文獻[29]通過試驗給出式(12)中系數α、c4、c0與阻尼器輸入電壓v符合以下線性關系：

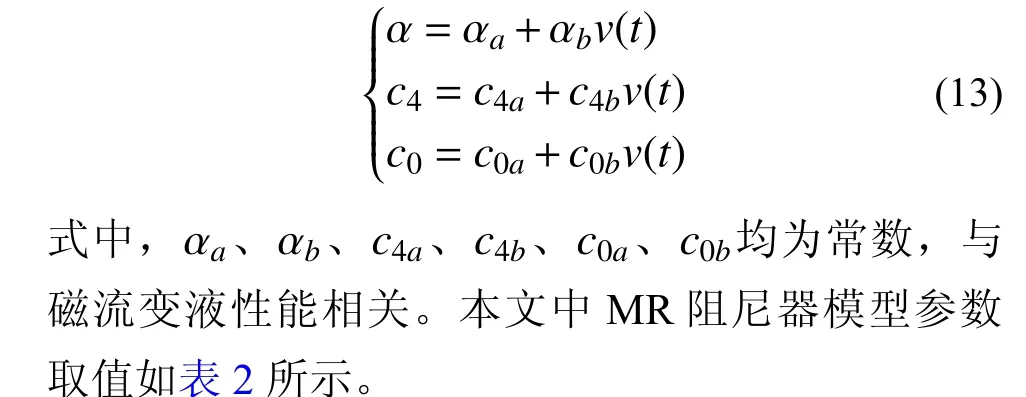
將結構底層速度、位移的誤差及誤差變化率作為控制算法的輸入，將MR 阻尼器阻尼力作為輸出。為驗證控制算法的有效性，選取如圖6 所示的0.34g南北向EI Centro 波進行激勵。

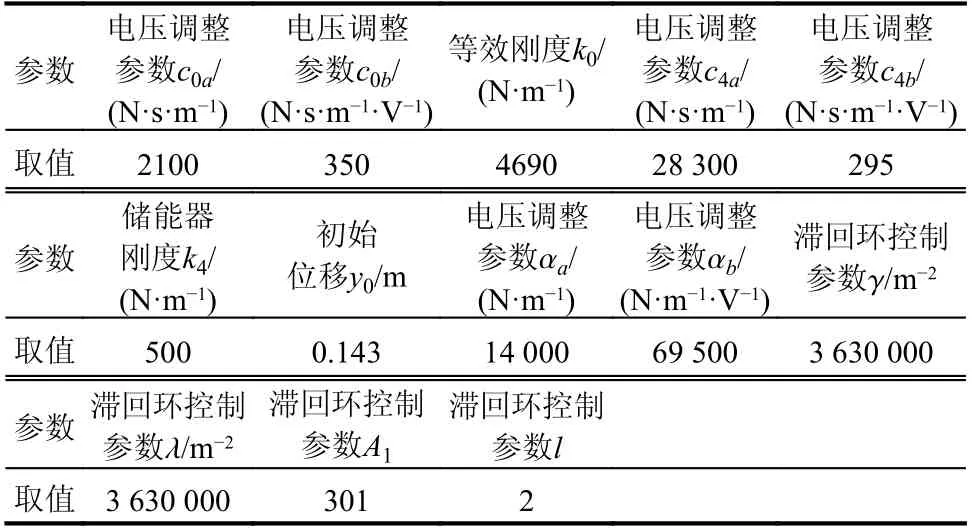
表2 MR 阻尼器參數取值Table 2 The value of parameters of the MR damper

圖6 南北向EI Centro 波加速度曲線Fig. 6 The acceleration curve of the north-south EI Centro wave

分別采取無控、PID 控制、VUFP 控制和NEVUFP 控制方法進行對比分析，并以結構頂層相對位移、絕對速度和絕對加速度峰值作為控制效果評價指標。其中，對于PID 控制，采用臨界比例法[30]設計三個參數Kp=2.97、Ki=72.74、Kd=0.004；對于VUFP 控制，τ1、τ2、τ3、τ4分別取為0.95、0.98、0.95、0.98；對于NEVUFP，按第2 節設計控制系統。

3.2 仿真結果

限于篇幅，僅給出結構頂層相對位移時程曲線，如圖7 所示。從圖7 可以看出，在無控狀態下結構頂層相對位移峰值高達10.34 mm，而在PID 控制、VUFP 控制、NEVUFP 控制作用下，分別降低至4.835 mm、4.021 mm 和3.528 mm，控制率分別為53.24%、61.12%、65.88%，表明以上控制算法均能有效抑制結構位移響應，其中NEVUFP 算法控制效果最佳。

圖7 頂層位移時程曲線Fig. 7 The time history curve of the displacement of top floor

結構各樓層相對位移響應峰值及控制率如表3所示。在不同控制算法下，結構相對位移響應峰值及控制率均隨著樓層的增高而逐漸降低，其中NEVUFP 算法減振效果明顯優于PID 和VUFP 控制算法。這主要是由于NEVUPF 算法能在線調整伸縮因子參數，使MR 阻尼器的輸入參數更加精確，從而提供更為準確的阻尼力。

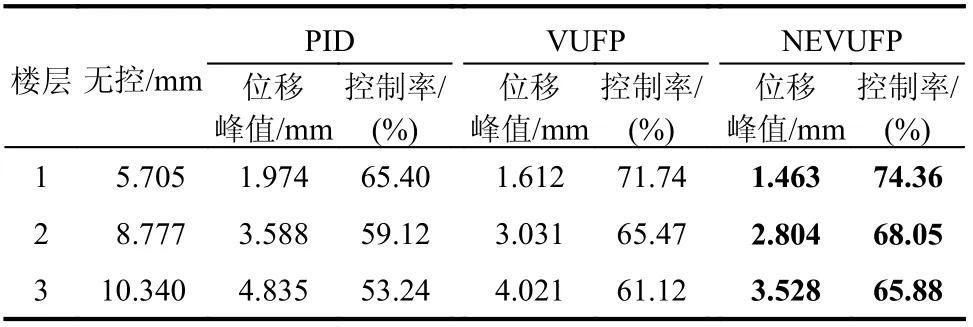
表3 結構各層相對位移峰值及控制率Table 3 The peak values and control rates of the relative displacement of each floor

本文僅給出伸縮因子參數τ1的時程變化曲線，如圖8 所示。在不同時間步，伸縮因子τ1根據e和ec實時調整，其中τ1最大變化(約0.8)發生在EI 波峰值(約2.04 s)處，主要原因在于此時結構振動最大，所產生的系統誤差也往往最大，根據第1 節中伸縮因子的模糊控制規則，此時需較大調整τ1方能對結構實施高效控制。因此，NEVUFP 算法能在不依賴專家知識或工程經驗的前提下，實現伸縮因子參數自適應調整，從而施加更為有效的控制參數。

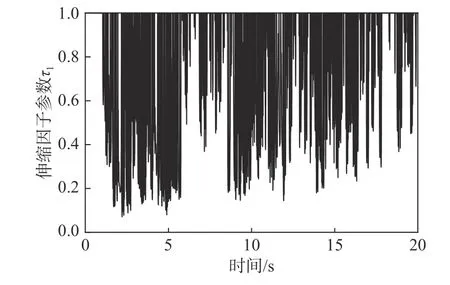
圖8 參數τ1 變化時程曲線Fig. 8 The time history curve of τ1

4 振動臺試驗

4.1 實驗系統簡介

在實驗室搭建3 層單跨鋼框架結構，結構開間、進深和層高分別為600 mm、400 mm 和512 mm。樓層由600 mm×400 mm×6 mm 鋼板組成；柱由鋼管組成，所有鋼管尺寸為500 mm×16 mm×2 mm，鋼管兩端焊接70 mm×70 mm×6 mm 的矩形連接板，并通過4 顆螺栓和鋼板連接。底層每根鋼管通過4 顆螺栓與800 mm×800 mm×10 mm 鋼板固定，然后，將該鋼板固定在振動臺上。每層樓板均配重10 kg 鐵塊。RD-8041-1 MR 阻尼器以37.06°傾角安裝在結構底層，一端與第一層樓板固定，一端與振動臺上剛性框架固定，如圖9 所示。

圖9 半主動控制實驗圖Fig. 9 Experimental setup of the semi-active control

在各層布設P15H-2 壓電加速度傳感器、941B速度傳感器和磁致伸縮位移傳感器，并采用dsPACE 1303 實時仿真系統中的MicroLabBox 模塊進行數據采集。通過dsPACE 調用編譯好的控制算法來計算結構所需控制力，再通過數模轉化模塊(D/A)、電流驅動器將信號傳輸給MR 阻尼器，從而實現框架結構的半主動控制。

分別采用EI Centrol 波和Taft 波對鋼框架進行單向激勵(圖9 中x向)，采用結構底層速度、位移的誤差及誤差變化率作為輸入，對各層加速度、速度及位移進行同步控制。對PID、VUFP 和NEVUFP控制算法進行對比，其中，根據拼湊法[31]選取PID 中參數Kp=2.77、Ki=17.106、Kd=0.1496；通過現場試控制，VUFP 算法中τ1、τ2、τ3、τ4分別取0.65、0.2、0.65、0.2。

4.2 試驗結果

本文僅給出EI Centrol 波激勵下結構在實施VUFP、NEVUFP 控制前后頂層相對位移時程曲線，如圖10 所示。在實施VUFP、NEVUFP 控制后，結構頂層相對位移響應明顯降低，而NEVUFP算法具有更好的控制效果。

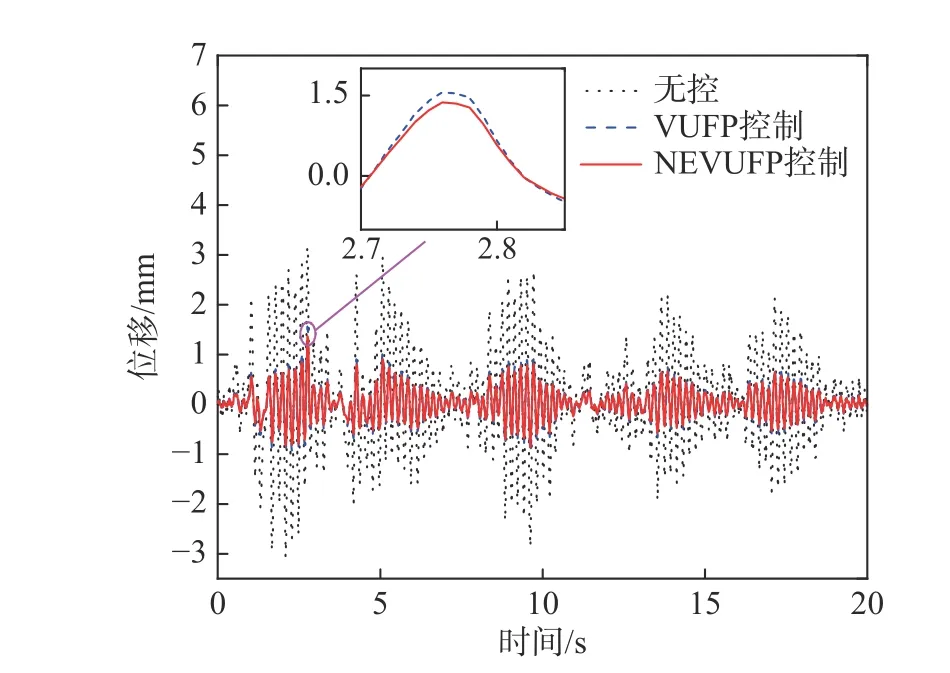
圖10 頂層相對位移時程曲線Fig. 10 The time history curve of the relative displacement of top floor

在地震波作用下結構各樓層加速度、位移的最大峰值響應如圖11 所示。在PID、VUFP 和NEVUFP 控制算法作用下，結構頂層加速度峰值由5634 mm/s2分別降低至3595 mm/s2、3333 mm/s2和1805 mm/s2，減振率分別為36.18%、40.84%、67.96%；結構相對位移峰值由3.15 mm 分別降低至1.63 mm、1.56 mm 和1.37 mm，減振率分別為48.25%、50.48%、56.51%。結果表明，兩種地震波下NEVUFP 算法均具有更好的控制效果。

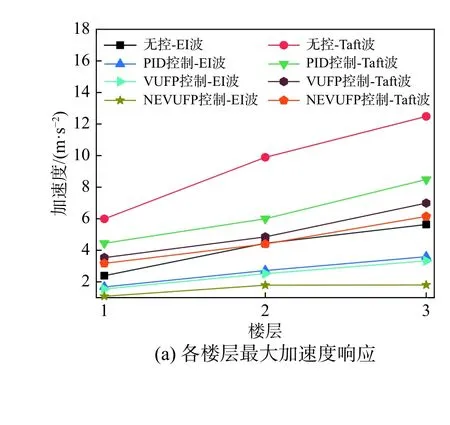
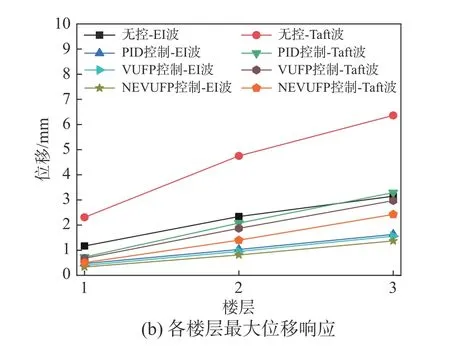
圖11 各控制算法下結構加速度及位移最大值Fig. 11 The peak values of the accelerate and displacement of each floor

5 結論

針對傳統變論域模糊(VUFP)控制算法中伸縮因子參數缺乏明確物理意義、無法自適應調整的問題，提出了自適應變論域模糊控制方法。采用理論推導證明了所提新型函數型伸縮因子的穩定性，并通過數值算例與振動臺試驗驗證了所提方法的適用性。所得結論如下：

(1)在假定輸入、輸出變量伸縮因子設計參數相等(τ1=τ2=τ3=τ4)的前提下，通過理論證明了新型伸縮因子滿足對偶性、非零性、單調性、正規性和協調性條件，從理論上闡明了所提算法的穩定性；

(2)在選取比例指數函數模型伸縮因子的前提下，根據系統誤差及誤差變化率，構建了伸縮因子參數的數學模型，實現了伸縮因子參數的自適應變化；

(3)三層框架數值算例結果表明，NEVUFP 控制方法相比于PID、VUFP 控制算法，在頂層相對位移方面分別提高12.64%、4.77%，說明本文方法的控制效果較好；

(4)振動臺試驗結果表明，針對三層框架結構頂層位移，相比于PID、VUFP 算法，NEVUFP 算法在EI Centrol 波作用下控制率分別提高8.26%、6.04%，在Taft 波作用下控制率分別提高13.61%、8.58%，這表明所提方法對實際結構在地震作用下的振動控制具有較好適用性。