軸向往復荷載作用下圓鋼管混凝土柱恢復力模型研究

蔡文哲，史慶軒，王 斌

(1. 西安工程大學城市規劃與市政工程學院，陜西，西安 710055；2. 西安建筑科技大學土木工程學院，陜西，西安 710055)

現階段，我國高層建筑設計正朝著“適用、經濟、綠色、美觀”的方向發展，因而需要適應性強、整體剛度大、經濟高效的新型結構體系。基于建筑需求與結構需求，斜交網格筒結構體系近年來得到廣泛關注[1]，如美國IBM 大樓、瑞士再保險大廈、阿聯酋的“首都之門”、韓國第一高樓樂天大廈。在我國斜交網格筒結構體系也已應用于廣州西塔、大連石油大廈、深圳創業投資大廈等工程。斜交網格筒結構體系多建于經濟發達的高烈度區，但對于此類結構在大震作用下損傷機理的研究滯后于工程實際，現有抗震設計方法也只局限于彈性設計，較為保守。國內外學者[2-6]對斜交網格結構進行了彈塑性分析，研究了其在水平和豎向荷載作用下斜柱的內力分布，指出鋼管混凝土斜柱主要承受軸向拉壓往復荷載。關 于 構 件 方 面，Zhou 等[7]、Kim 等[8]、Han等[9-10]對斜交網格結構中的相貫節點開展了擬靜力試驗研究，分析了相貫節點在軸力作用下的受力性能。

斜柱作為斜交網格筒結構體系的主要承力構件，兼具了一般框架-支撐結構中直柱和斜撐的功能，在地震作用下將承受軸向往復拉壓荷載，因而其受力性能也將顯著區別于傳統壓彎構件。傳統壓彎構件[11]推拉方向受力是對稱的，其所得到的滯回曲線和恢復力模型也是對稱的，而軸向受力的鋼管混凝土柱拉壓方向受力機理是不同的，因此軸拉和軸壓方向鋼管混凝土柱的滯回曲線和恢復力模型具有不對稱性，但國內外對于承受軸向往復荷載作用的鋼管混凝土柱的抗震性能研究較少，也未建立起相應的恢復力模型，有必要對其恢復力特性展開專門研究。

近年來國內外學者[12-14]以鋼管混凝土構件的抗震性能試驗為基礎，將恢復力模型進行了簡化，開展了不同構件在不同受力狀態下的恢復力模型參數識別等研究工作。臧興震[15]提出了鋼管約束型鋼高強混凝土柱的三線型恢復力模型，張向岡[16]采用無量綱化坐標提出了鋼管再生混凝土構件的三折線恢復力模型，定義了屈服點、峰值點和下降段剛度，給出了計算各特征點的表達式，但所提模型僅適用于承受水平荷載的壓彎構件，不能體現出斜交網格結構中鋼管混凝土柱軸壓和軸拉狀態的不對稱性，且沒有定義裂縫滑移點。然而，目前關于軸向往復荷載作用下鋼管混凝土構件的恢復力模型的研究極少涉及，由于此類構件特有的受力機理和恢復力特性，特征點及卸載剛度都需重新標定。

為此，本文基于鋼管混凝土柱的軸向往復加載試驗結果，選用退化三線型模型，建立鋼管混凝土柱無量綱骨架曲線模型，并提出其軸拉與軸壓方向的峰值承載力和位移的計算方法。鑒于鋼管混凝土柱在軸拉和軸壓狀態下性能的差異，在滯回曲線正負向選用不同的滯回規則，建立相應的卸載剛度函數，最終提出一套完整的適合于承受軸向往復荷載的鋼管混凝土柱恢復力模型，并通過與試驗滯回曲線的對比，驗證恢復力模型的合理性。

1 鋼管混凝土柱抗震性能試驗研究

1.1 試驗概況

參考廣州西塔中的鋼管混凝土斜柱，設計制作了8 個鋼管混凝土柱試件，具體設計參數見表1，主要考察混凝土強度、加載路徑、長徑比和含鋼率對其軸向恢復力特性的影響。在鋼管兩端均焊接一塊鋼蓋板以便對試件加載和約束，并通過設置加勁肋以保證加載板與鋼管混凝土間的傳力能力，如圖1 所示。試驗采用C40 和C50 兩種混凝土，加載前其實測軸心抗壓強度分別為38.31 MPa和46.69 MPa，直徑為140 mm 和133 mm 的兩種鋼管屈服強度分別為324 MPa 和308 MPa，具體的試件設計詳見文獻[17]。

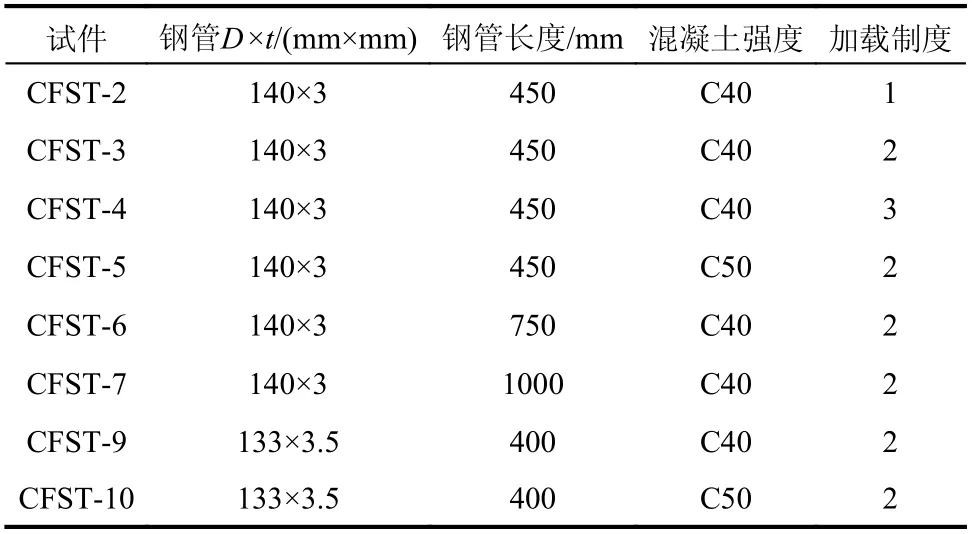
表1 試件設計Table 1 Specimens design

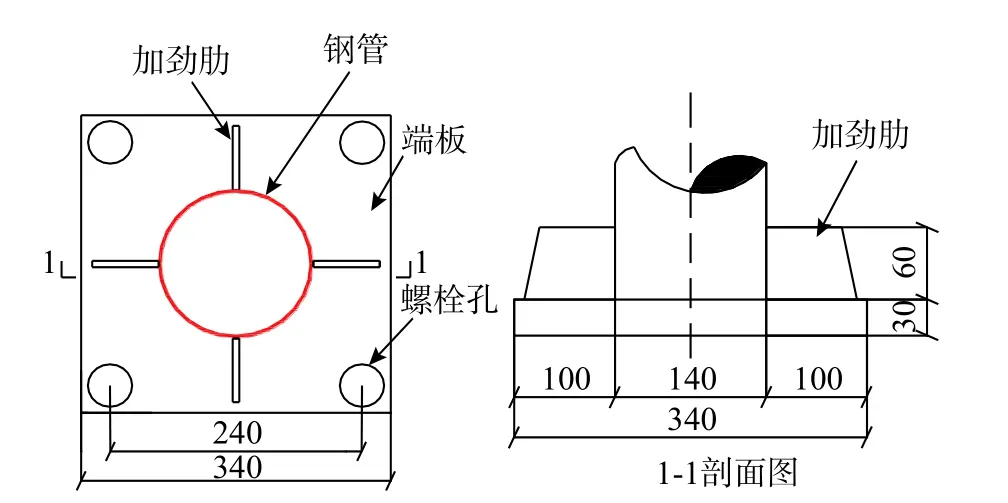
圖1 端部蓋板設置 /mmFig. 1 Setting of cover plate

通過將門架和作動器水平放置設計出如圖2所示的自平衡加載裝置，在加載軸兩側對稱布置兩個1000 kN 作動器，并在加載過程中保持其協同工作，試驗中以推向為正，拉向為負，具體加載裝置如圖2 所示。

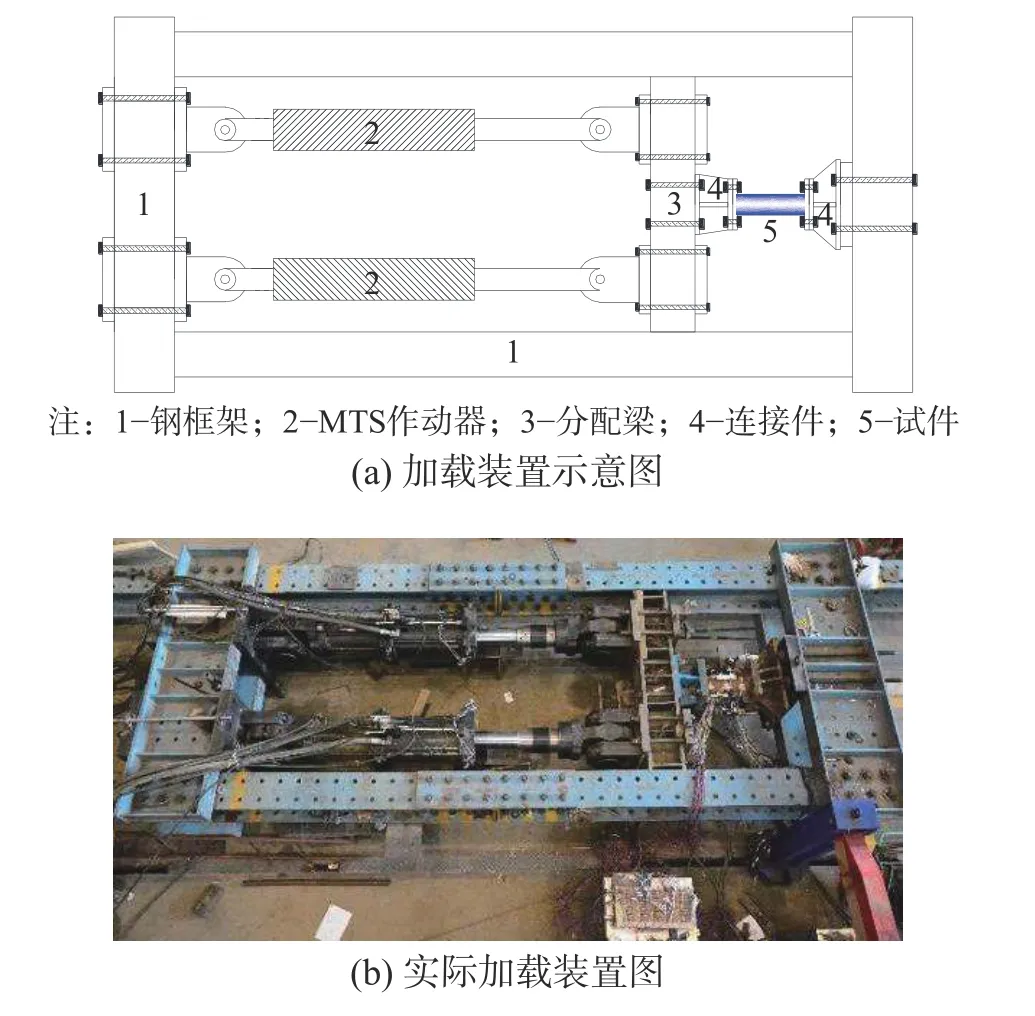
圖2 軸向往復加載試驗裝置Fig. 2 Axial cyclic loading test setup

現有研究表明，地震作用下斜交網格筒結構體系中的斜柱所受軸向拉壓力幅值變化明顯，因此試驗中選用3 種不同加載方式來研究其恢復力性能，另外，由于鋼管混凝土試件推拉方向的承載力和變形能力也不對稱，因此在其推拉方向選用不對稱加載制度。通過荷載-位移控制[18]模式施加軸向往復荷載，試件屈服前，通過荷載控制加載，每級荷載循環一次，基于前期有限元分析結果，選定推/拉荷載極差為100 kN/50 kN，以控制試件在兩個方向均達到屈服。試件屈服后，通過在屈服位移的基礎上施加一定位移增量進行加載，每級位移循環三次，加載制度1、2、3 在推/拉方向位移極差分別為0.5 mm/1 mm、0.5 mm/0.5 mm、1 mm/0.5 mm，至試件承載力下降至峰值荷載的85%時停止加載。

本次試驗主要采集軸向荷載、軸向變形和鋼管應變數據，分別通過作動器力傳感器、兩蓋板間位移計以及鋼管表面應變花來獲取數據，試驗后提取試件鋼管端部和中部的應變數據[19]，可以看出鋼管縱向應變沿環向分布均勻，進一步驗證了加載裝置可以確保試件軸向受力。

1.2 試驗破壞形態

加載過程中試件表現為：混凝土開裂-鋼管屈服-鋼管外鼓-鋼管開裂-鋼管局部屈曲-鋼管斷裂。試件屈服前鋼管和混凝土獨立工作，屈服之后，核心混凝土與鋼管開始發生相互作用，在軸拉方向，混凝土開裂后基本不再繼續承受軸拉力，主要對鋼管起到支撐作用；在軸壓方向，鋼管屈服之后，所受軸向壓力逐漸減小，鋼管對混凝土的約束作用使得混凝土所受軸壓力逐漸增大，二者所受壓力重新分布直至達到軸壓方向承載力。

典型試件及其核心混凝土的破壞形態如圖3所示，試件端部鋼管斷裂，核心混凝土基本保持完好，只有端部的核心混凝土被壓碎，其中試件CFST-5 由于選用了C50 的混凝土，出現了更為嚴重的混凝土破碎現象。另外，各試件核心混凝土均存在一系列環向裂縫和少量縱向裂縫，未出現斜裂縫，說明試件均為軸心受力，未出現偏心和扭轉現象。

圖3 試件和核心混凝土的破壞形態Fig. 3 Failure modes of specimens and core concrete

1.3 試驗滯回曲線

試驗得到的試件荷載-位移滯回曲線如圖4 所示，由圖可知：設計在軸拉與軸壓方向的受力表現出不同的受力特性，滯回曲線不對稱，試件受壓方向具有相對較高的剛度和承載力，而受拉方向具有更好的變形和耗能能力。另外，試件恢復力特性在兩個方向上的也表現出明顯不同，從軸拉至軸壓時，試件恢復力曲線表現出明顯的捏攏效應，這是由于試件在受拉時核心混凝土會出現較多環向裂縫，荷載反向至軸壓力時裂縫隨即閉合，并且試件的鋼管與混凝土之間的粘結滑移也會導致滯回曲線的捏縮；而從軸壓至軸拉時，恢復力曲線光滑飽滿，未出現捏攏效應，這是由于試件受壓時鋼管與混凝土協同工作，未出現明顯的粘結滑移，且受壓時核心混凝土基本未出現裂縫，荷載反向時剛度變化連續。

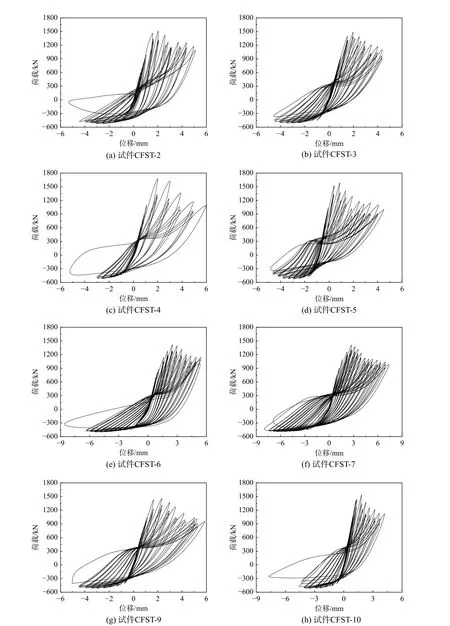
圖4 試驗滯回曲線Fig. 4 Hysteretic loops of specimens

2 骨架曲線模型

本文基于鋼管混凝土柱的軸向往復加載試驗結果，采用數據擬合的方法來確定骨架曲線的關鍵點。考慮到鋼管混凝土柱軸拉與軸壓方向承載力、剛度和極限變形能力的差異，分別建立其不同受力方向的骨架曲線。鑒于試驗試件設計參數的不同，導致各試件承載力及其對應的位移差異較大，基于絕對量值計算出的骨架曲線關鍵點具有較大的離散性。因此，本章將鋼管混凝土柱的骨架曲線簡化為基于峰值荷載與峰值位移的無量綱化三折線型骨架曲線來標定此類構件的特征點。

2.1 無量綱化骨架曲線

簡化的無量綱骨架曲線模型如圖5 所示，A點、B點和C點依次表示軸壓方向上的屈服點、峰值點和極限點；A′點、B′點和C′依次表示軸拉方向上的屈服點、峰值點和極限點，對8 個鋼管混凝土柱試驗結果進行無量綱化處理，得到特征點的荷載和位移，如表2 所示。

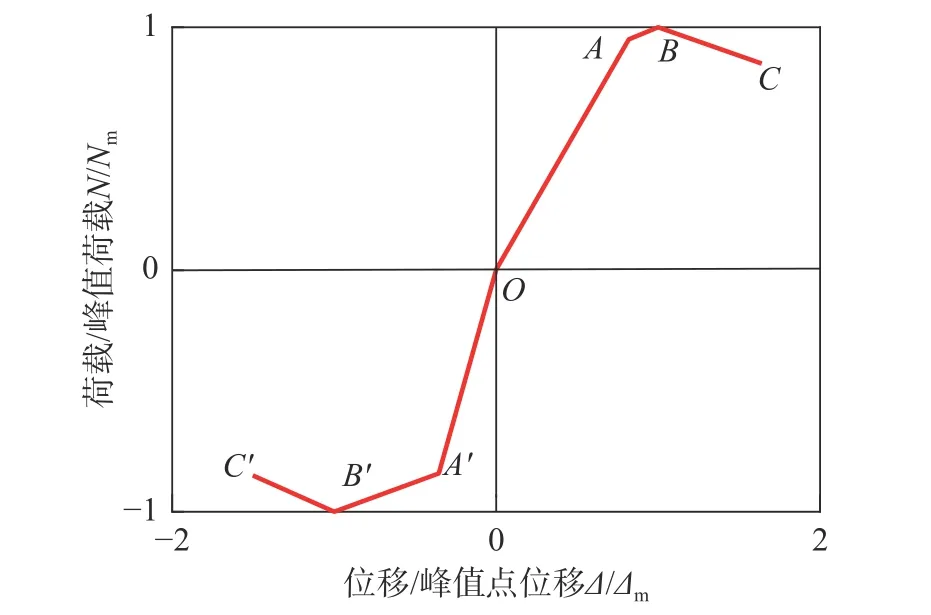
圖5 骨架曲線模型Fig. 5 Skeleton curve model

通過對表2 中特征點數據的回歸分析，擬合出無量綱骨架曲線，各折線段方程如下:

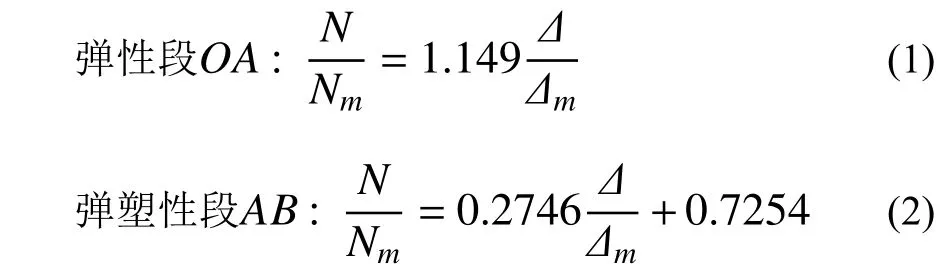
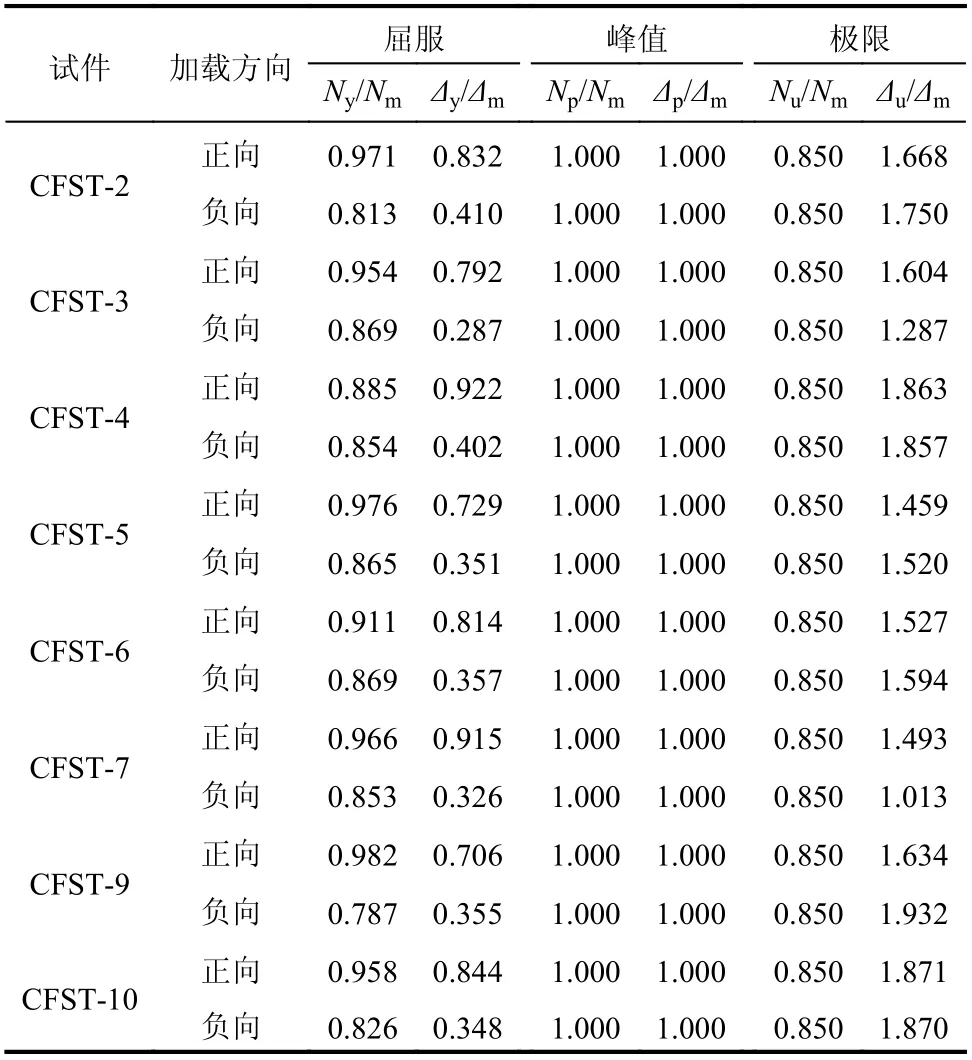
表2 無量綱化荷載和位移Table 2 Dimensionless load and displacement

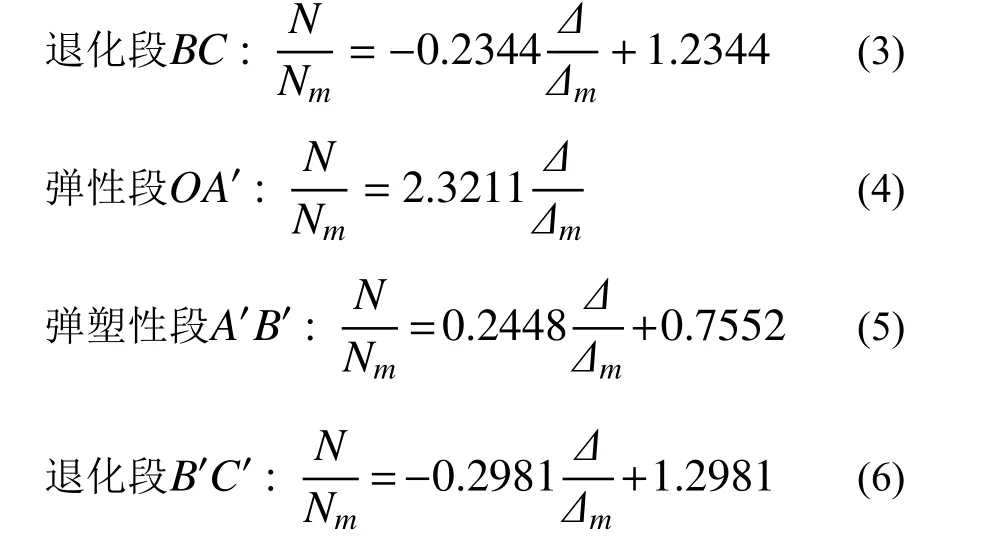
2.2 峰值荷載與峰值位移的計算

1)軸壓方向

基于蔡紹懷提出的極限平衡法[20]，對鋼管混凝土柱在軸壓方向的承載力進行了分析，計算簡圖如圖6 所示：N為外荷載；σc為混凝土縱向應力；σ1和σ2分別為鋼管的縱向應力為和環向應力；p為鋼管與混凝土界面之間的側向壓力。

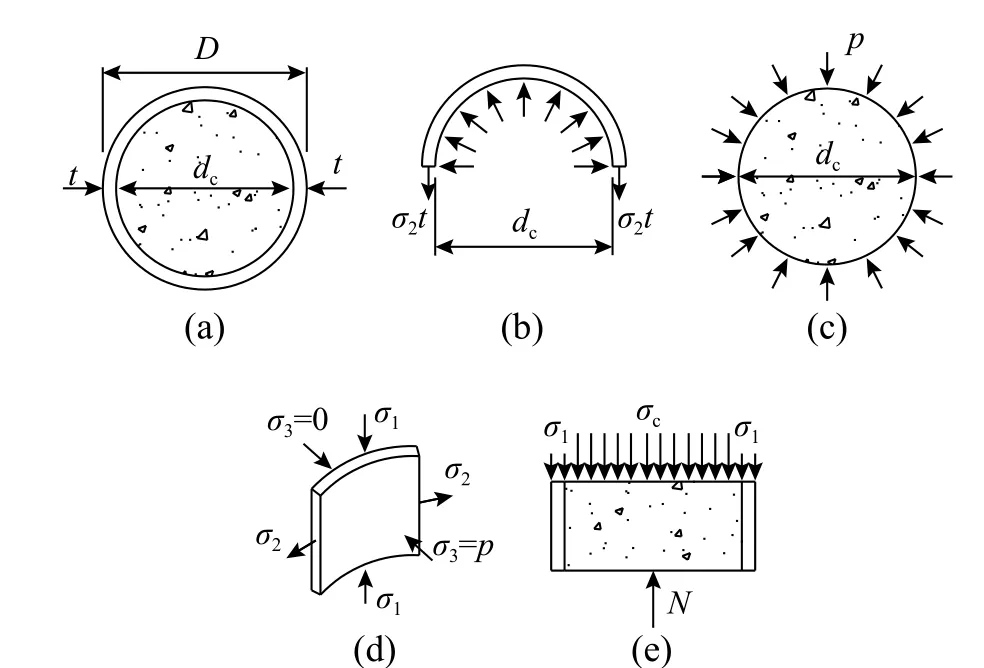
圖6 鋼管和核心混凝土的受力簡圖Fig. 6 Stress diagram of steel tube and core concrete

極限平衡法假定：

① 鋼管混凝土柱被視為由鋼管和核心混凝土兩種要素組成的結構體系。

② 鋼管采用Von Mises 屈服條件，表達式為：

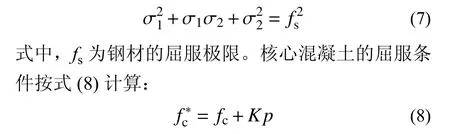
式中：fc為混凝土的抗壓強度；K為側壓力系數；f*c為核心混凝土在三向受壓時的強度。

③ 在極限狀態下，對于D/t≥20 的薄壁鋼管，徑向應力σ3的影響可以忽略不計。鋼管的應力狀態可以簡化為縱向受壓和環向受拉的雙向應力狀態，并沿管壁均勻分布。

式中，α1為鋼管混凝土柱在拉壓往復荷載作用下考慮材料性能退化的軸壓承載力折減系數，將式(12)計算出的軸壓承載力Nuc與軸向往復試驗和數值模擬得出的承載力進行線性擬合，如圖7所示，得到α1=0.95。

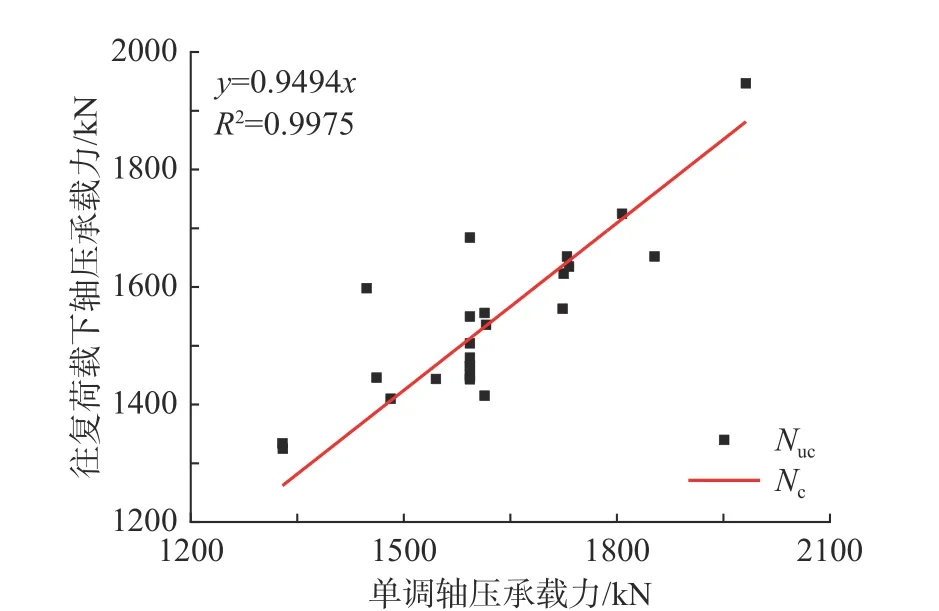
圖7 受壓承載力擬合Fig. 7 Fitting of compressive capacity

根據韓林海[21]提出的圓鋼管混凝土軸壓峰值點的應變計算公式：

2)軸拉方向

目前國內外對鋼管混凝土構件軸拉性能的研究較少，由于鋼管在加載后期的應變強化現象明顯，偏于安全的考慮一般取鋼管縱向應變為10 000 με時的軸拉力為鋼管混凝土構件極限承載力[22]，因此軸拉峰值點對應的位移為：

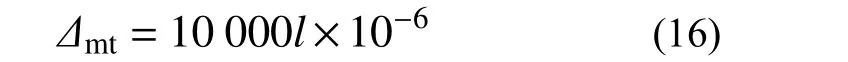
由于本次試驗結束時所有試件的鋼管均已被拉斷，因此計算軸拉承載力時應取鋼材的極限強度，此時混凝土已完全被拉裂，僅考慮混凝土對鋼管的支撐作用。參照《鋼管混凝土結構技術規范》(GB 50936-2014)[23]中提出鋼管混凝土構件軸心受拉承載力計算公式：

式中：Nut為鋼管混凝土構件軸心受拉承載力；C1為鋼管受拉強度提高系數；f為鋼材極限強度，依據文獻[24]對于實心截面取C1=1.12-0.05ξ。由于試件最終于鋼管受壓屈曲處發生斷裂破壞，因此，認為鋼管的受壓屈曲產生的損傷使得受拉方向承載力發生折減。考慮到拉壓往復荷載作用的損傷累積，引入受拉承載力折減系數α2，提出軸向拉壓往復荷載作用下鋼管混凝土柱的受拉承載力公式：

同樣，將式(17)計算出的軸壓承載力Nut與軸向往復試驗和數值模擬的承載力進行線性擬合，如圖8 所示，得到α2=0.97。

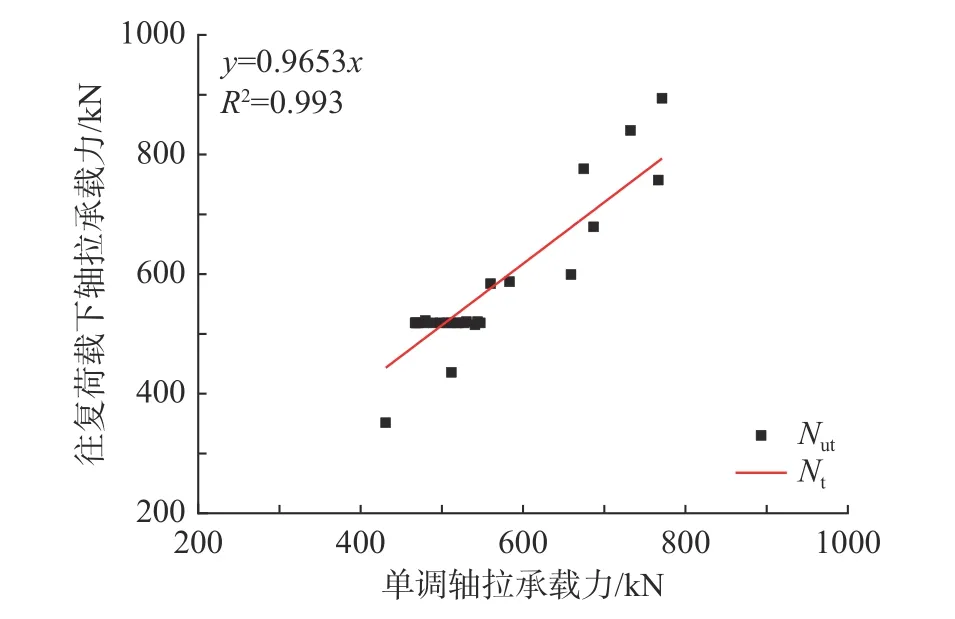
圖8 受拉承載力擬合Fig. 8 Fitting of tensile capacity

3 滯回準則

由于試件滯回曲線表現出了一定的捏攏效應，本文選用捏攏型滯回規則，該規則包含卸載和反向加載兩個階段，由于試件在不同受力方向表現出了不同的恢復力特征，通過兩段指向點定義的不同和卸載剛度的差異來區分鋼管混凝土柱在軸拉和軸壓狀態下滯回規則的差異。圖9 定義了軸向往復加載下鋼管混凝土柱的滯回規則，下文將就其走勢和卸載剛度的計算進行詳細解釋。

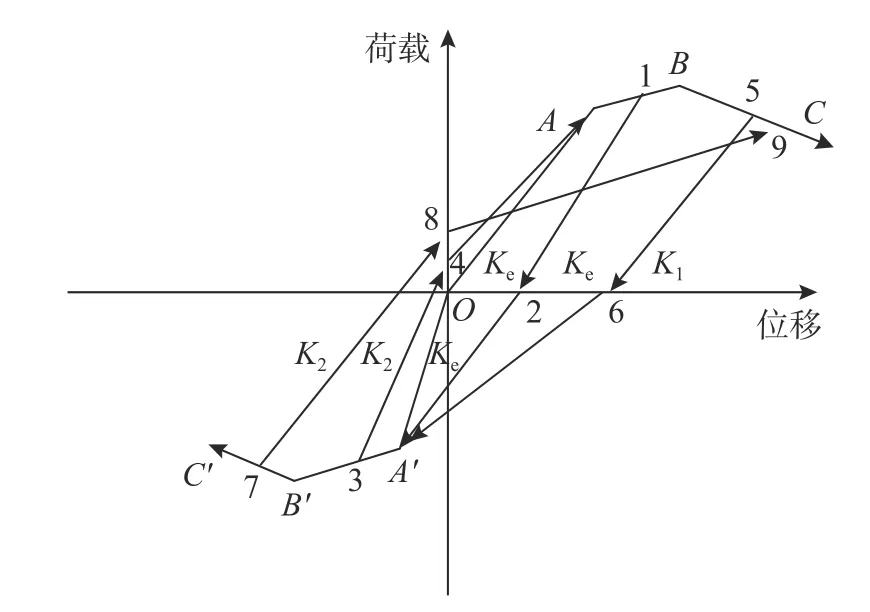
圖9 滯回規則示意圖Fig. 9 Diagrammatic sketch of hysteresis

3.1 軸壓至軸拉狀態

1)彈性段加卸載規則

在試件屈服前，按彈性剛度加卸載。

2)彈塑性上升段加卸載規則

恢復力達到正向屈服荷載之后且未超過峰值承載力時，按骨架曲線加載。卸載段(點1 至點2)指向橫坐標軸，由于此階段卸載剛度退化不明顯，卸載剛度取為彈性剛度Ke。從點2 即縱坐標為0 時開始反向加載，指向負向屈服點A′并沿負向骨架曲線加載至點3，之后按照負向卸載規則卸載。

3)彈塑性下降段加卸載規則

恢復力達到峰值荷載后，卸載段(點5 至點6)同樣指向橫坐標軸，但卸載剛度已明顯退化，卸載剛度K1需依據試驗結果擬合出的公式計算。從點6 即縱坐標為0 時開始反向加載，指向負向屈服點A′并沿負向骨架曲線加載至點7，之后按照負向卸載規則卸載。

為了建立卸載剛度K1的計算表達式，圖8 給出了各試驗試件下降段正向卸載剛度與彈性剛度之比K1/Ke隨無量綱位移Δ/Δm的變化關系，通過對試驗數據的回歸分析，發現K1/Ke與Δ/Δm近似呈指數關系，因此采用指數函數進行非線性擬合，擬合曲線見圖10，進而得到正向卸載剛度的計算表達式：

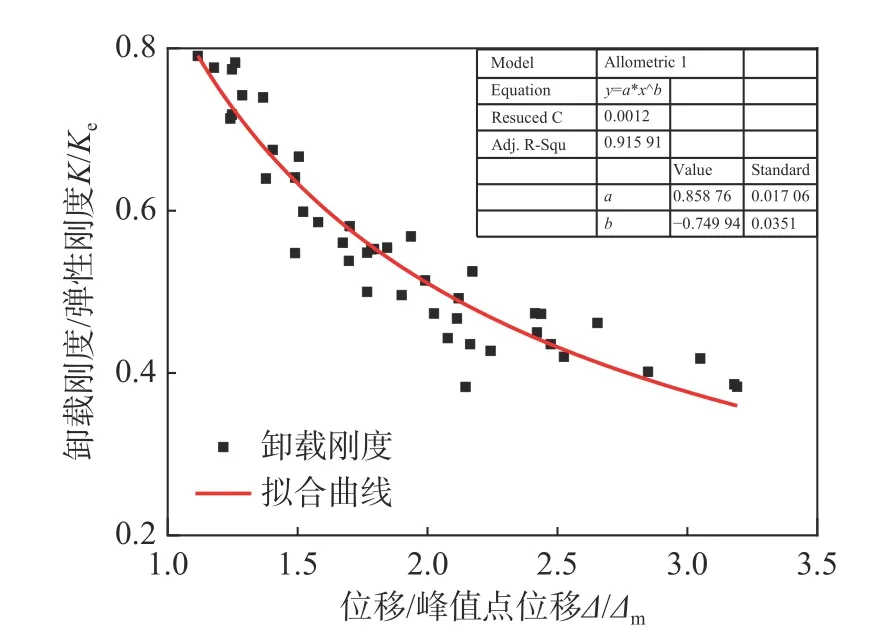
圖10 正向至負向卸載剛度擬合曲線Fig. 10 Fitting curve of positive to negative unloading stiffness

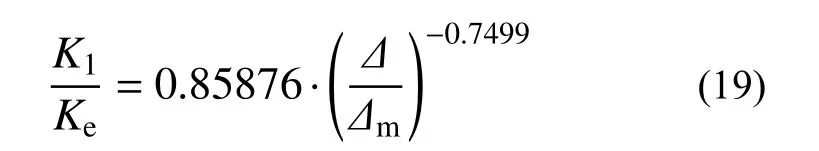
擬合曲線的相關系數R=0.957，擬合參數a和b的標準差分別為0.017、0.035，表明采用上述函數類型進行回歸是合理的，且擬合公式達到了足夠的精度。在本文研究的含鋼率與長細比參數范圍內，可用于鋼管混凝土柱軸向恢復力模型的計算。

3.2 軸拉至軸壓狀態

負向卸載與正向卸載的主要區別是混凝土裂縫閉合發生滑移造成的捏攏效應，加載初期混凝土就出現裂縫，但總變形不大，捏攏效應并不明顯，因此認為試件受拉屈服之后卸載剛度才開始發生退化。

1)彈性段加卸載規則

在試件屈服前，按彈性剛度加卸載。

2)彈塑性上升段加卸載規則

恢復力達到負向屈服荷載之后且未超過峰值承載力時，按骨架曲線加載。卸載段(點3 至點4)依據試驗曲線指向縱坐標軸，此階段卸載剛度已開始逐步退化，因此卸載剛度K2需依據試驗結果擬合出的公式計算。從點4 即橫坐標為0 時開始反向加載，指向正向屈服點A并沿正向骨架曲線繼續加載，之后按照正向卸載規則卸載。

3)彈塑性下降段加卸載規則

恢復力達到峰值荷載后，卸載段(點7 至點8)同樣指向縱坐標軸，卸載剛度K2也仍需依據試驗結果擬合出的公式計算。從點8 即縱坐標為0 時開始反向加載，但不再指向正向屈服點A，而是指向骨架曲線上的下一個目標位移點9，點9 的位置通過目標位移和骨架曲線來確定，之后按照正向卸載規則卸載。

為了建立卸載剛度K2的計算表達式，圖11給出了各試驗試件整個彈塑性階段(上升段和下降度)負向卸載剛度與彈性剛度之比K2/Ke隨無量綱位移Δ/Δm的變化關系，通過對試驗數據的回歸分析，發現在整個塑性階段K2/Ke與Δ/Δm近似呈指數關系，因此同樣采用指數函數進行非線性擬合，擬合曲線見圖11，進而得到負向卸載剛度的計算表達式：

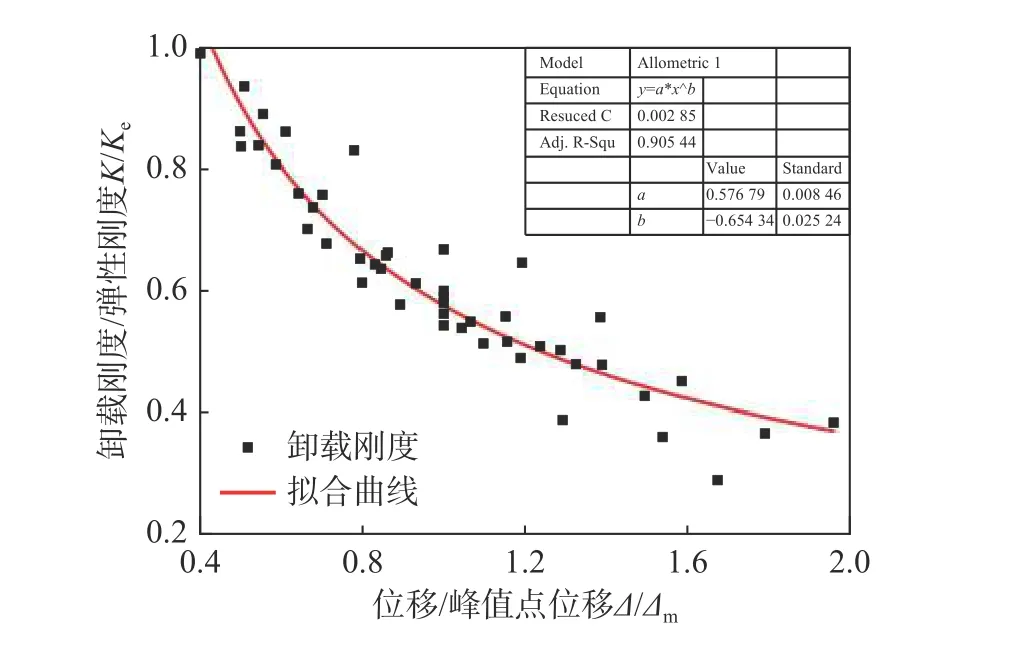
圖11 負向至正向卸載剛度擬合曲線Fig. 11 Fitting curve of negative to positive unloading stiffness

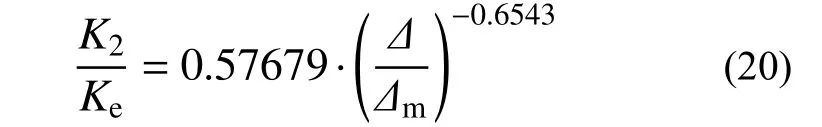
擬合曲線的相關系數R=0.952，擬合參數a和b的標準差分別為0.008 和0.025，表明式(20)可作為鋼管混凝土柱恢復力模型中滯回規則的標定依據。

4 恢復力模型與試驗結果的對比

至此本文已構建了一個完整的恢復力模型，首先利用所建立的承載力模型與峰值位移關系計算出骨架曲線，再通過卸載剛度退化公式求出卸載剛度，并結合滯回規則，即可計算鋼管混凝土試件的滯回曲線。圖12 對比了鋼管混凝土柱試驗滯回曲線與恢復力模型計算結果。可以看出，試驗與計算滯回曲線的形狀和走勢都吻合良好，但由于本文采用了三折線模型，存在突變點，而試驗曲線相對更為飽滿。總體來看，本文所建立的恢復力模型已達到足夠的精度，可準確預測軸向往復荷載作用下鋼管混凝土柱的荷載-位移滯回關系。因此，采用本文恢復力模型計算結果可為斜交網格結構體系在大震作用下的抗震性能研究提供理論基礎。

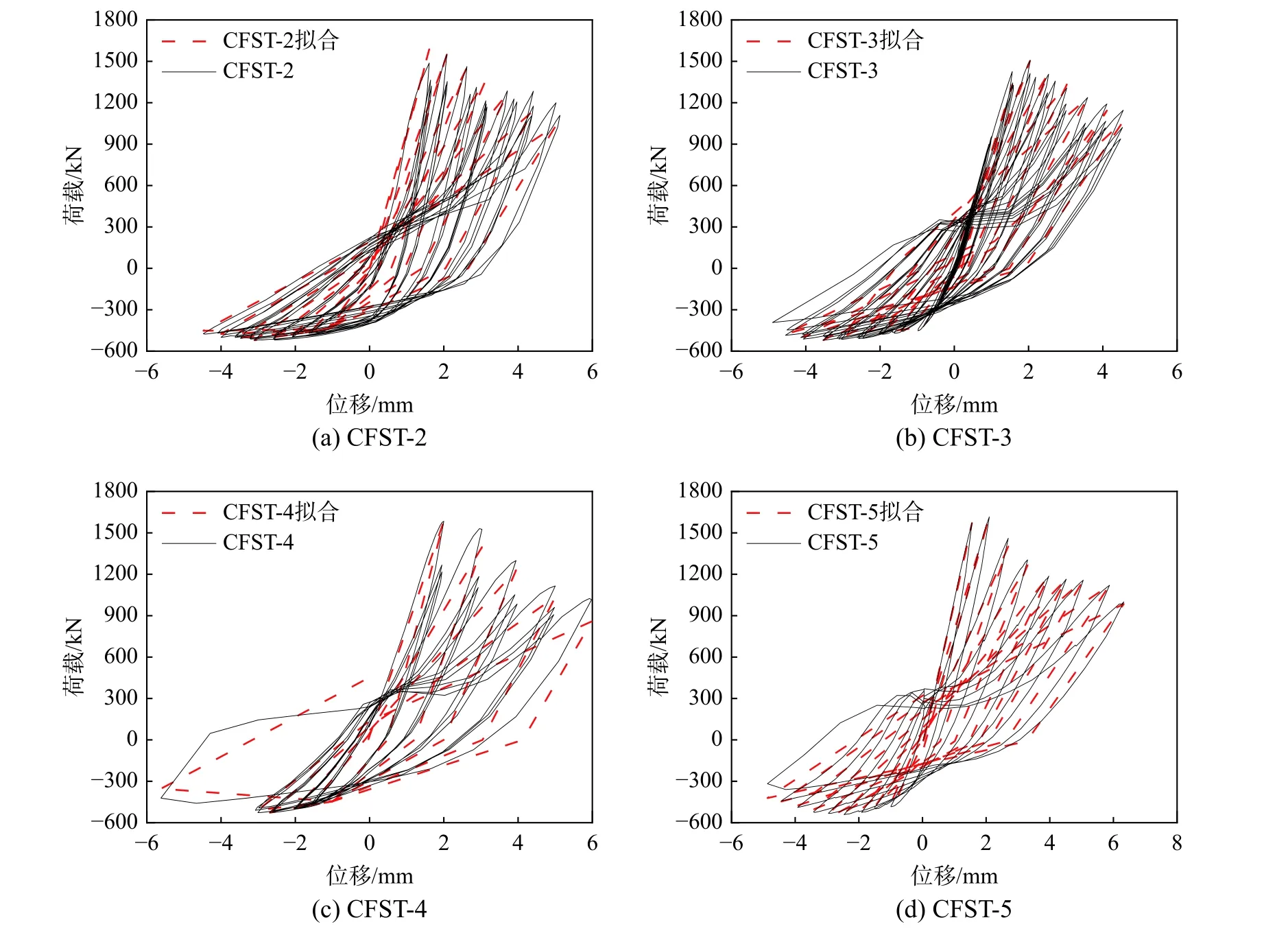
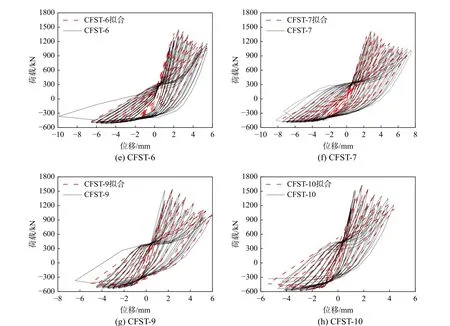
圖12 試驗與計算滯回曲線對比Fig. 12 Comparison of hysteresis curve between test and calculation

5 結論

本文以斜交網格結構體系中的鋼管混凝土斜柱為研究對象，通過8 個鋼管混凝土柱的擬靜力加載試驗，研究了其在軸向往復荷載作用下的恢復力特性，并基于試驗結果提出了約束效應系數介于0.6～1.2 和長徑比介于3.2～7.1 的鋼管混凝土柱軸向恢復力模型，主要結論如下：

(1)鋼管混凝土柱的恢復力特性在拉壓方向不對稱，從受拉至受壓時，試件恢復力曲線表現出捏縮現象，而從受壓至受拉時，恢復力曲線剛度變化連續，光滑飽滿，未出現捏攏效應。

(2)選用退化三線型模型，建立了無量綱化骨架曲線模型，并建立了鋼管混凝土柱的軸壓與軸拉承載力計算公式，考慮軸向往復荷載引起的損傷提出了相應的承載力折減系數，并提出了峰值位移的計算表達式，構建了一個完整的骨架曲線模型。鑒于鋼管混凝土試件在軸拉與軸壓方向受力機理的差異，對滯回曲線的正負向選用不同的滯回規則，分別建立了相應的卸載剛度函數。

(3)基于本文建立的骨架曲線模型與滯回準則，計算出鋼管混凝土柱的滯回曲線，與試驗滯回曲線吻合良好，說明本章建立的恢復力模型可合理預測軸向往復荷載作用下鋼管混凝土柱的滯回行為，所建立的恢復力模型可為斜交網格結構體系的彈塑性分析提供依據。