近斷層SV波斜入射下瀝青混凝土心墻壩響應(yīng)分析
劉 琳, 宋志強(qiáng), 王 飛, 劉云賀
(西安理工大學(xué) 省部共建西北旱區(qū)生態(tài)水利國(guó)家重點(diǎn)實(shí)驗(yàn)室,西安 710048)
瀝青混凝土心墻壩具有適應(yīng)變形能力強(qiáng)、防滲性能好和工程造價(jià)低等優(yōu)點(diǎn)[1],是水資源開(kāi)發(fā)利用的優(yōu)選壩型之一。我國(guó)水資源豐富的西部地區(qū),已建或即將建設(shè)一批瀝青混凝土心墻壩。這些地區(qū)的地質(zhì)斷層活躍且強(qiáng)震頻發(fā),瀝青混凝土心墻壩的抗震安全面臨嚴(yán)峻挑戰(zhàn)。傳統(tǒng)的瀝青心墻壩抗震研究常以遠(yuǎn)場(chǎng)地震動(dòng)記錄作為地震動(dòng)輸入,少有區(qū)分近斷層與遠(yuǎn)斷層地震動(dòng)[2]。
近年來(lái),許多學(xué)者研究表明近斷層地震動(dòng)具有明顯的脈沖特性,對(duì)結(jié)構(gòu)響應(yīng)具有顯著影響[3-4]。近斷層地震動(dòng)作用下壩體的響應(yīng)研究大多集中在重力壩和拱壩,李明超等[5-7]發(fā)現(xiàn)近斷層地震動(dòng)會(huì)給重力壩的損傷累積破壞帶來(lái)嚴(yán)重影響;杜修力等[8]研究發(fā)現(xiàn)拱壩重要部位的位移、加速度等動(dòng)力響應(yīng)的幅值放大系數(shù)隨著剪切波入射角度變化而顯著變化。近斷層地震動(dòng)作用下土石壩的抗震性能研究主要在混凝土面板堆石壩,Zou等[9-10]發(fā)現(xiàn)近斷層地震動(dòng)垂直入射下壩體位移、加速度和面板應(yīng)力均隨著PGV/PGA增大而增大,并建議對(duì)強(qiáng)震地區(qū)的混凝土面板堆石壩進(jìn)行近斷層脈沖型地震動(dòng)專(zhuān)門(mén)研究。
目前針對(duì)瀝青混凝土心墻壩的近斷層地震動(dòng)斜入射研究尚不多見(jiàn),現(xiàn)有研究在近斷層地震動(dòng)輸入方面,多是假定垂直入射[11],實(shí)際上近斷層地震動(dòng)由于斷層距較近,地震波經(jīng)過(guò)極其有限次的反射和透射后到達(dá)地表,一般不滿足垂直入射的假定。因此有必要開(kāi)展近斷層脈沖型地震動(dòng)斜入射下瀝青混凝土心墻壩的響應(yīng)研究。本文通過(guò)斜入射波動(dòng)輸入模擬瀝青混凝土心墻壩遭受近斷層SV波作用過(guò)程,分析了近斷層地震動(dòng)的脈沖特性、入射角度對(duì)心墻加速度、應(yīng)力和壩體永久變形的影響規(guī)律。為強(qiáng)震地區(qū)瀝青混凝土心墻壩的抗震設(shè)計(jì)提供參考。
1 近斷層地震動(dòng)的選取
本文從太平洋地震工程研究中心(PEER)數(shù)據(jù)庫(kù)中選取中國(guó)臺(tái)灣集集近斷層脈沖型和無(wú)脈沖地震動(dòng)記錄各5條[12],如表1所示。近斷層地震動(dòng)與遠(yuǎn)場(chǎng)地震動(dòng)的區(qū)分是以斷層距20 km為指標(biāo),而脈沖和無(wú)脈沖地震動(dòng)的區(qū)分指標(biāo)是PGV/PGA的比值和PGA的值,即此比值大于0.2、PGA大于0.1g的記錄視為脈沖型地震動(dòng)。因此,本文選擇地震動(dòng)記錄盡量保證PGV/PGA值在脈沖、無(wú)脈沖地震動(dòng)定義范圍內(nèi)相對(duì)均勻分布。
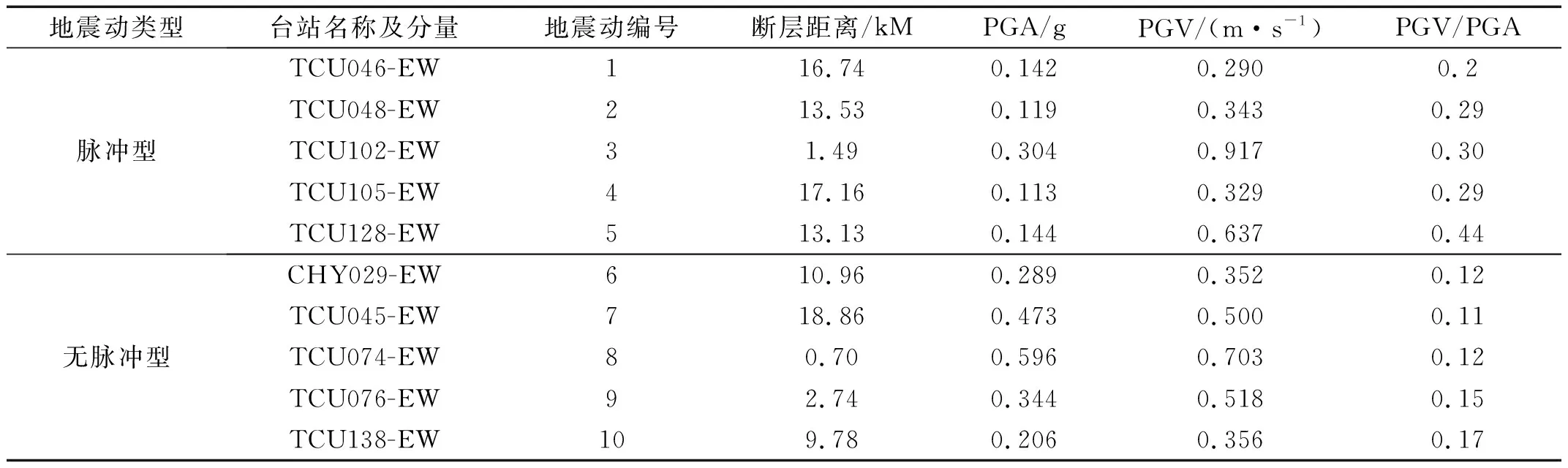
表1 近斷層地震動(dòng)記錄
脈沖和無(wú)脈沖地震動(dòng)的速度、位移差異如圖1、圖2所示,脈沖型地震動(dòng)與無(wú)脈沖型地震相比,具有明顯的速度、位移脈沖且持時(shí)短。以PGA相似的TCU102(0.304g)、TCU076(0.344g)臺(tái)站記錄為例,脈沖型(TCU102)地震動(dòng)記錄的PGV是無(wú)脈沖型(TCU076)地震動(dòng)記錄的1.77倍,PGD是無(wú)脈沖型(TCU076)地震動(dòng)的3.14倍。
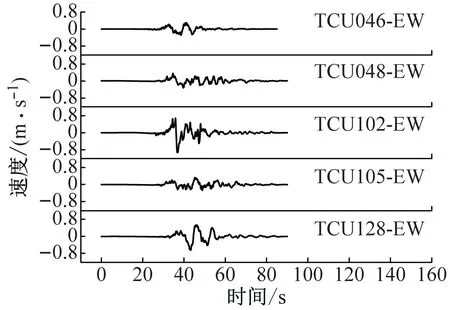
(a) 脈沖地震動(dòng)速度時(shí)程
圖3為脈沖型地震動(dòng)與無(wú)脈沖型地震動(dòng)的譜加速度,結(jié)構(gòu)自振周期未達(dá)到0.25 s時(shí),無(wú)脈沖地震動(dòng)譜加速度均值大于脈沖地震動(dòng)譜加速度均值;結(jié)構(gòu)自振周期達(dá)到0.4 s后,脈沖型地震動(dòng)的譜加速度均值顯著大于非脈沖型地震動(dòng)譜加速度。百米級(jí)瀝青混凝土心墻壩的自振周期在1 s左右,圖3表明脈沖型地震動(dòng)對(duì)瀝青混凝土心墻壩的影響遠(yuǎn)大于無(wú)脈沖型地震動(dòng)。
2 地震動(dòng)斜輸入方法
本文采用黏彈性人工邊界模擬無(wú)限地基輻射阻尼效應(yīng),地震動(dòng)的輸入問(wèn)題轉(zhuǎn)化為邊界上等效節(jié)點(diǎn)力處理問(wèn)題。式(1)給出了黏彈性人工邊界等效節(jié)點(diǎn)力計(jì)算公式
(1)
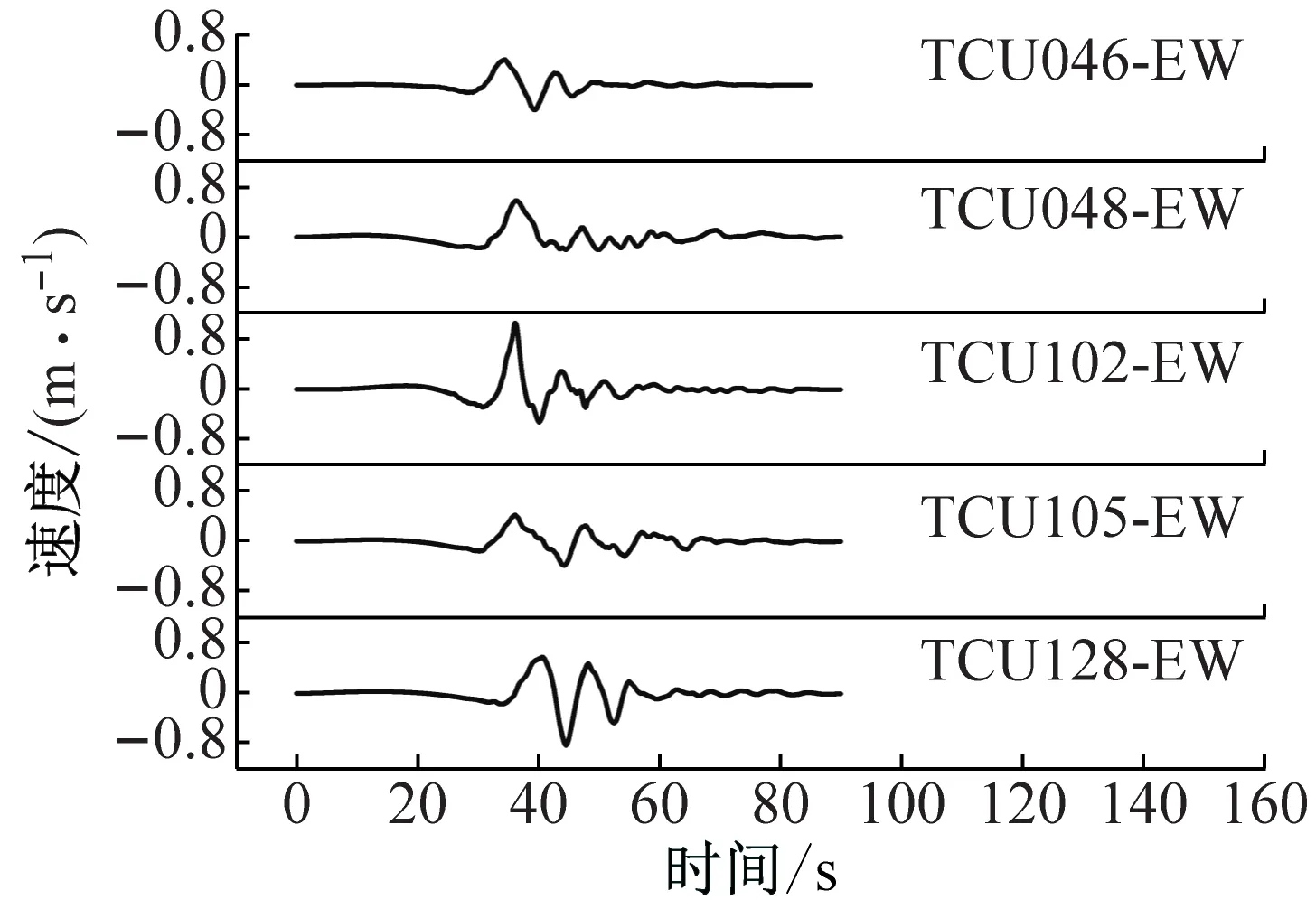
(a) 脈沖地震動(dòng)位移時(shí)程
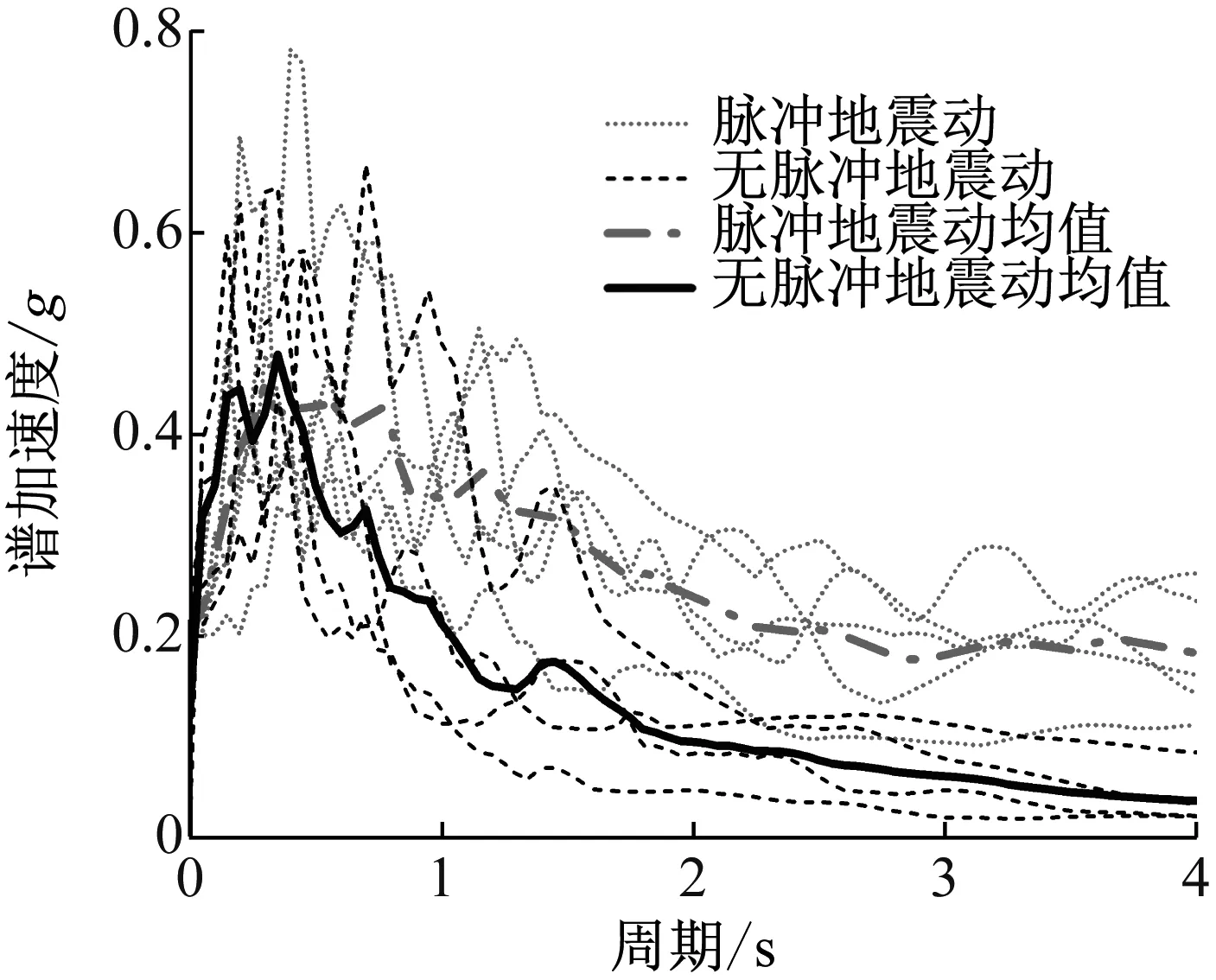
圖3 脈沖型和非脈沖地震動(dòng)加速度譜Fig.3 Acceleration spectra of pulse-like and non-pulse groundmotions
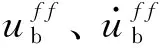
在地震動(dòng)斜入射過(guò)程中,波場(chǎng)分解方法是一個(gè)關(guān)鍵問(wèn)題[13],不同的波場(chǎng)分解方法會(huì)導(dǎo)致地基各邊界面施加的等效節(jié)點(diǎn)力不同,最終影響計(jì)算結(jié)果的精度。當(dāng)前學(xué)者對(duì)地震波斜入射的波場(chǎng)分解方案尚未達(dá)成一致:SV波左側(cè)斜入射時(shí),左邊界面波場(chǎng)統(tǒng)一分解為入射SV波、反射SV波和反射P波,區(qū)別在于底邊界和右邊界的波場(chǎng)分解。黃景琦[14]認(rèn)為底、右邊界需同時(shí)入射SV波、反射SV波和反射P波;章小龍等[15]認(rèn)為底邊界可只考慮入射SV波,右邊界面考慮入射SV波、反射SV波和反射P波;汪精河等[16]認(rèn)為底邊界面為入射SV波,右邊界面則不需要考慮。實(shí)際上,斜入射時(shí)模型邊界上自由場(chǎng)波動(dòng)疊加越完整,計(jì)算結(jié)果越精確。因此,本文采用各邊界均完整考慮實(shí)際內(nèi)行波或外行波(或二者均存在)的波場(chǎng)分解方案,再考慮時(shí)間延遲進(jìn)行各波場(chǎng)疊加,進(jìn)而獲得該邊界自由場(chǎng)波動(dòng)。圖4給出了SV波左側(cè)斜入射時(shí),各邊界面由入射SV波、反射SV波和反射P波構(gòu)成的波場(chǎng)分解示意。從圖4可以看出,不同邊界面上的自由場(chǎng)存在較大差異,左側(cè)邊界自由場(chǎng)僅由內(nèi)行場(chǎng)構(gòu)成;底邊界自由場(chǎng)則包括內(nèi)行場(chǎng)和外行場(chǎng);右邊界則僅由外行場(chǎng)構(gòu)成,因此各邊界面上的等效節(jié)點(diǎn)力應(yīng)分別加以推導(dǎo)計(jì)算。
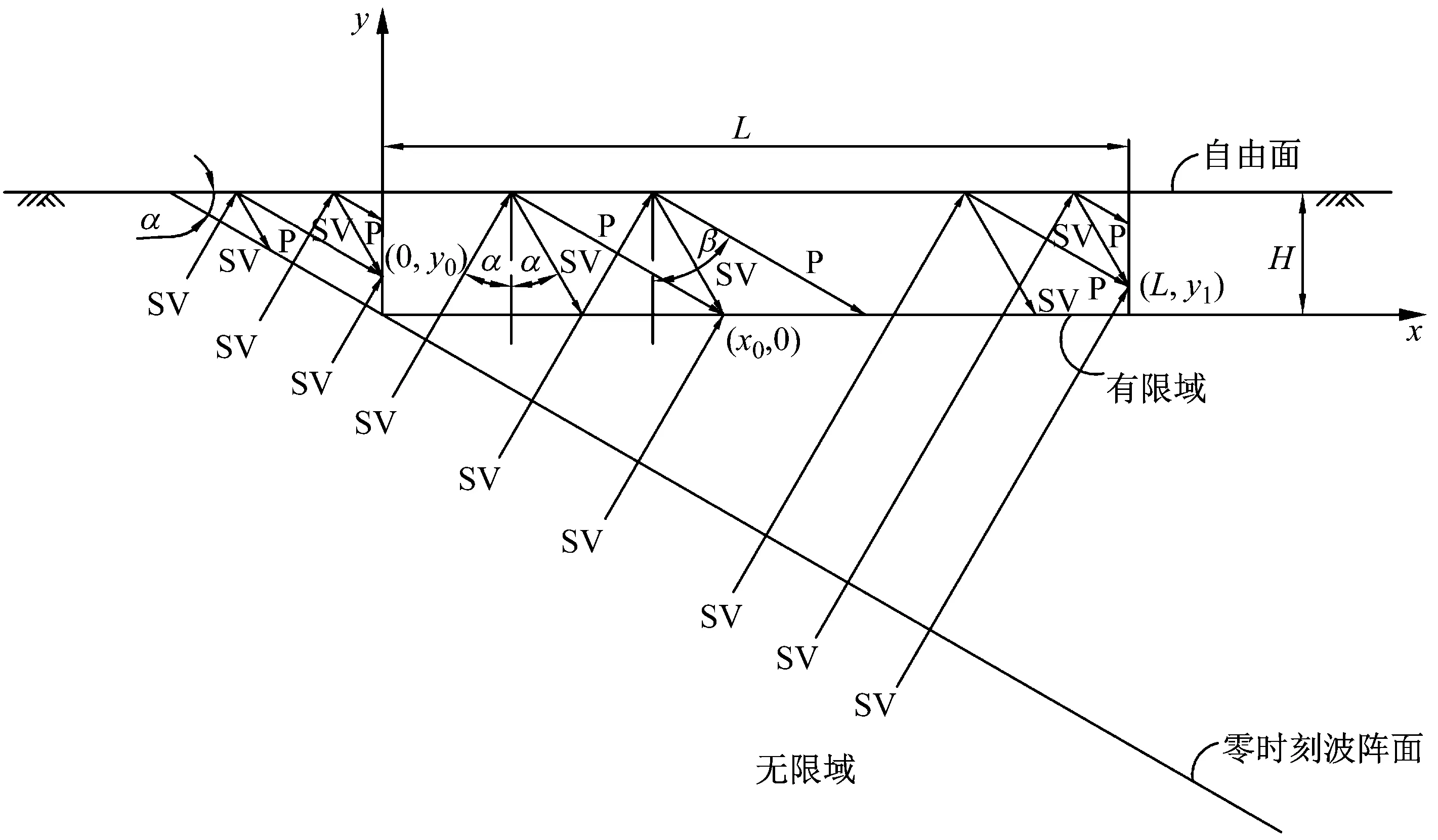
圖4 SV波斜入射示意圖
當(dāng)SV波斜入射時(shí),反射SV波與P波的振幅放大系數(shù)A1、A2及P波的反射角β計(jì)算如下
(2)
左邊界上任一點(diǎn)對(duì)于零時(shí)刻波陣面的延遲時(shí)間如式(3),其中Δt1、Δt2、Δt3分別為入射SV波、反射SV波和反射P波的延遲時(shí)間
(3)
左邊界面的位移場(chǎng)和速度場(chǎng)可以采用下式計(jì)算
(4)
(5)
左邊界面的應(yīng)力場(chǎng)可以通過(guò)彈性力學(xué)中的幾何方程和線彈性材料應(yīng)力-應(yīng)變關(guān)系得到
(6)
底邊界面的位移場(chǎng)和速度場(chǎng)同式(4)和式(5),只需將入射、反射SV波和反射P波的時(shí)間延遲分別換成Δt4、Δt5、Δt6,如式(7)所示;底邊界面的應(yīng)力場(chǎng)求法同左邊界面,如式(8)所示
(7)
(8)
右邊界面的位移場(chǎng)、速度場(chǎng)和應(yīng)力場(chǎng)的求法與左、底邊界面類(lèi)似,而位移場(chǎng)和速度場(chǎng)只需將式(4)和式(5)中的Δt1~Δt3分別換成Δt7~Δt9,詳細(xì)公式如下
(9)
(10)
3 瀝青混凝土心墻壩模型及參數(shù)
3.1 有限元模型概況
某瀝青混凝土心墻壩壩頂高程1 307.6 m,建基面平均高程1 223.5 m,壩頂寬度10 m,上游坡度為1∶2.25,下游坡度為1∶1.8,瀝青混凝土心墻為漸變式直心墻,頂部厚度為0.4 m,底部厚度為2 m。壩體和基礎(chǔ)整體有限元網(wǎng)格及材料分區(qū)如圖5所示。
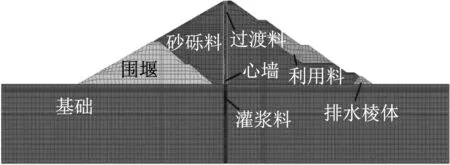
圖5 瀝青混凝土心墻壩有限元網(wǎng)格圖
3.2 本構(gòu)模型及材料參數(shù)
瀝青混凝土心墻壩的靜力計(jì)算本構(gòu)采用鄧肯張E-B非線性本構(gòu)模型[17]。動(dòng)力分析采用等效線性黏彈性本構(gòu)模型[18],通過(guò)迭代計(jì)算近似模擬土體的非線性。因?yàn)槊總€(gè)迭代過(guò)程都是線性的,此法計(jì)算效率高,尤其能對(duì)地震加速度小于0.4g的情況提供合理結(jié)果。模型中剪切模量、阻尼比與剪應(yīng)變的關(guān)系如式(11)~(13)
(11)
(12)
(13)
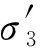
永久變形計(jì)算采用沈珠江殘余變形模型[19],殘余體應(yīng)變和殘余剪應(yīng)變?cè)隽啃问綖?/p>
(14)
(15)
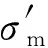
靜、動(dòng)力計(jì)算采用的材料參數(shù)分別如表2、表3所示。基巖采用線彈性模型,其中基巖的密度為2.7 g/cm3,彈性模量為2.97 GPa,泊松比為0.3。
3.3 計(jì)算工況
在正常蓄水位的情況下,將選取的10條近斷層脈沖型和無(wú)脈沖型地震動(dòng)分別以SV波按不同的角度從大壩上游傾斜入射。考慮到SV波斜入射時(shí)存在臨界入射角的情況,由基巖介質(zhì)內(nèi)SV波傳播波速650.44 m/s,則反射P波的傳播波速1 216.87 m/s,可知SV波斜入射的臨界角為32.31°,故本文將SV波最大斜入角度取為30°。各工況入射角度具體取值為0°、15°、25°和30°,為了避免不同地震動(dòng)記錄加速度峰值不同對(duì)計(jì)算結(jié)果造成影響,且考慮到該工程的地震設(shè)防烈度為Ⅷ度,將所選取的10條地震動(dòng)記錄的加速度峰值均調(diào)幅成0.2g。

表2 靜力計(jì)算參數(shù)

表3 動(dòng)力及永久變形計(jì)算參數(shù)
4 計(jì)算結(jié)果及分析
4.1 瀝青混凝土心墻壩加速度響應(yīng)
圖6給出了不同SV波入射角度下的心墻頂部水平、豎向加速度峰值。由圖可以看出,心墻頂水平向加速度峰值隨著入射角度的增大先略有減小后略有增加,但整體變化不大,豎向加速度對(duì)入射角增加較為顯著,主要是由于隨著入射角度的增加,地震動(dòng)的豎向分量逐漸增大。脈沖型地震動(dòng)作用下的響應(yīng)普遍大于無(wú)脈沖型地震動(dòng),當(dāng)入射角度為25°時(shí),脈沖型地震動(dòng)作用下壩體水平向和豎向加速度峰值的均值分別為無(wú)脈沖型的1.65倍和1.50倍。
圖7給出了SV波30°斜入射下各脈沖型和無(wú)脈沖型地震動(dòng)作用下的心墻水平和豎向加速度峰值沿高度分布。由圖可見(jiàn),各地震動(dòng)引起的墻頂加速度放大的鞭梢效應(yīng)明顯,脈沖型地震動(dòng)引起的心墻水平和豎向放大系數(shù)最大分別為4.25和1.77,而無(wú)脈沖型引起的放大系數(shù)最大為2.73和1.12。
4.2 瀝青混凝土心墻應(yīng)力
表4、表5統(tǒng)計(jì)了SV波斜入射時(shí)各角度、各地震動(dòng)記錄作用下心墻豎向拉應(yīng)力極值情況。從表可得:各入射角度下,脈沖型地震動(dòng)的豎向拉應(yīng)力均值都比無(wú)脈沖型大;脈沖型地震動(dòng)和無(wú)脈沖脈沖型地震動(dòng)產(chǎn)生的豎向拉應(yīng)力均隨著入射角度的增加而增加,在30°時(shí)達(dá)到最大,脈沖型最大為0.681 MPa,無(wú)脈沖型最大為0.266 MPa;脈沖、無(wú)脈沖地震動(dòng)30°入射時(shí)產(chǎn)生的豎向拉應(yīng)力均值比0°入射時(shí)分別增大了0.285 MPa、0.077 MPa。
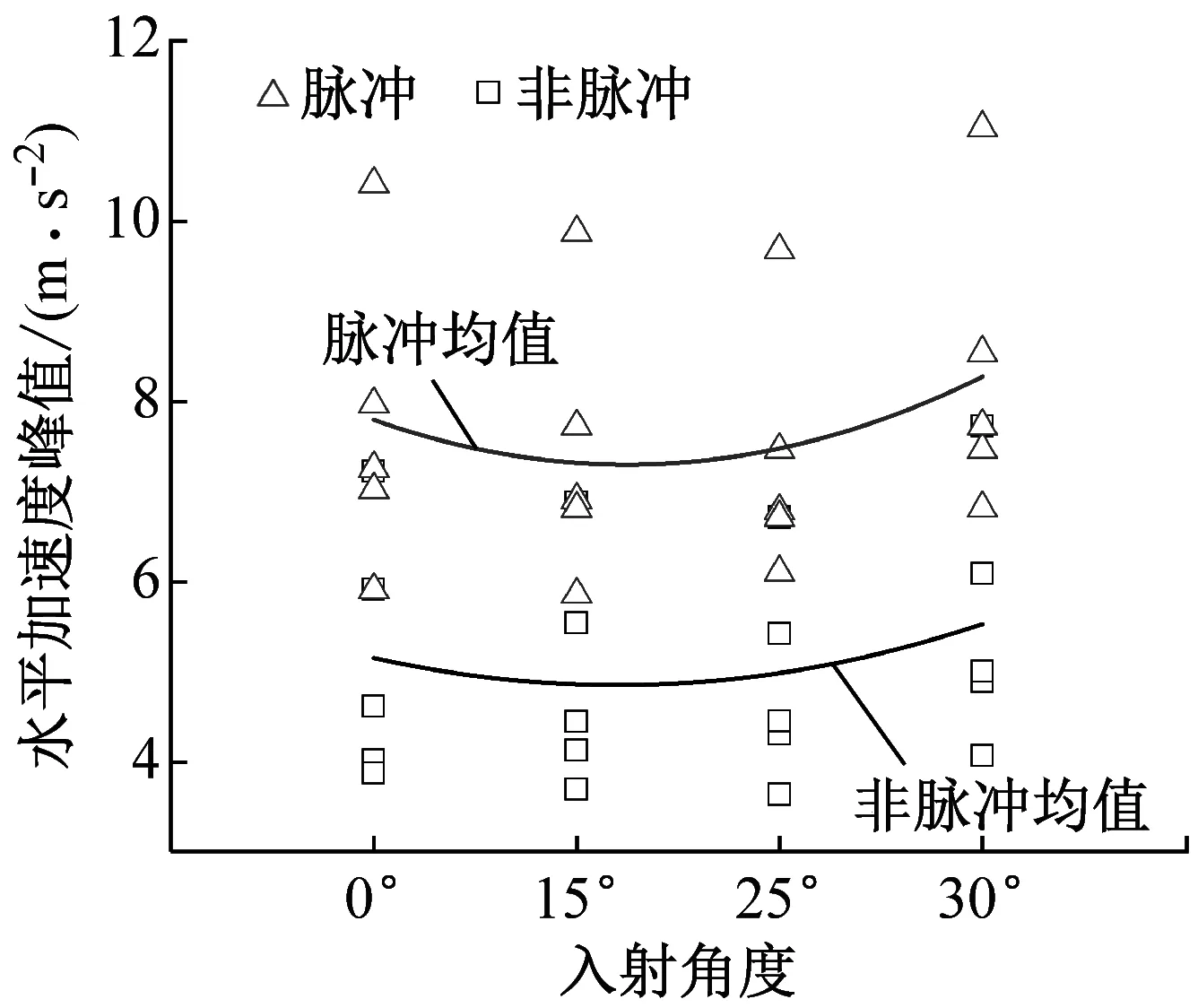
(a) 水平向
(b) 豎向圖6 不同入射角下心墻頂加速度峰值
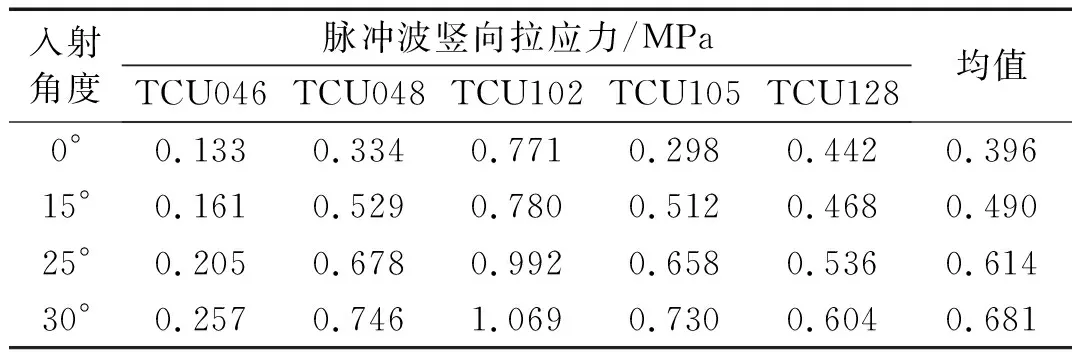
表4 各角度下脈沖波的心墻豎向拉應(yīng)力極值表
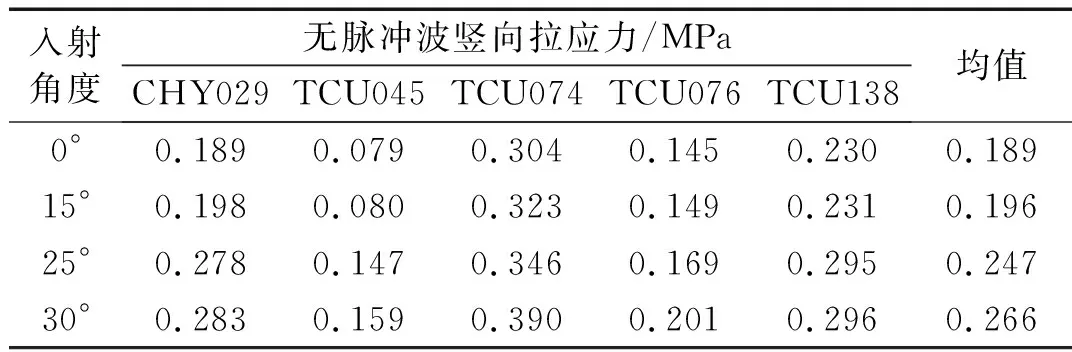
表5 各角度下無(wú)脈沖波的心墻豎向拉應(yīng)力極值表
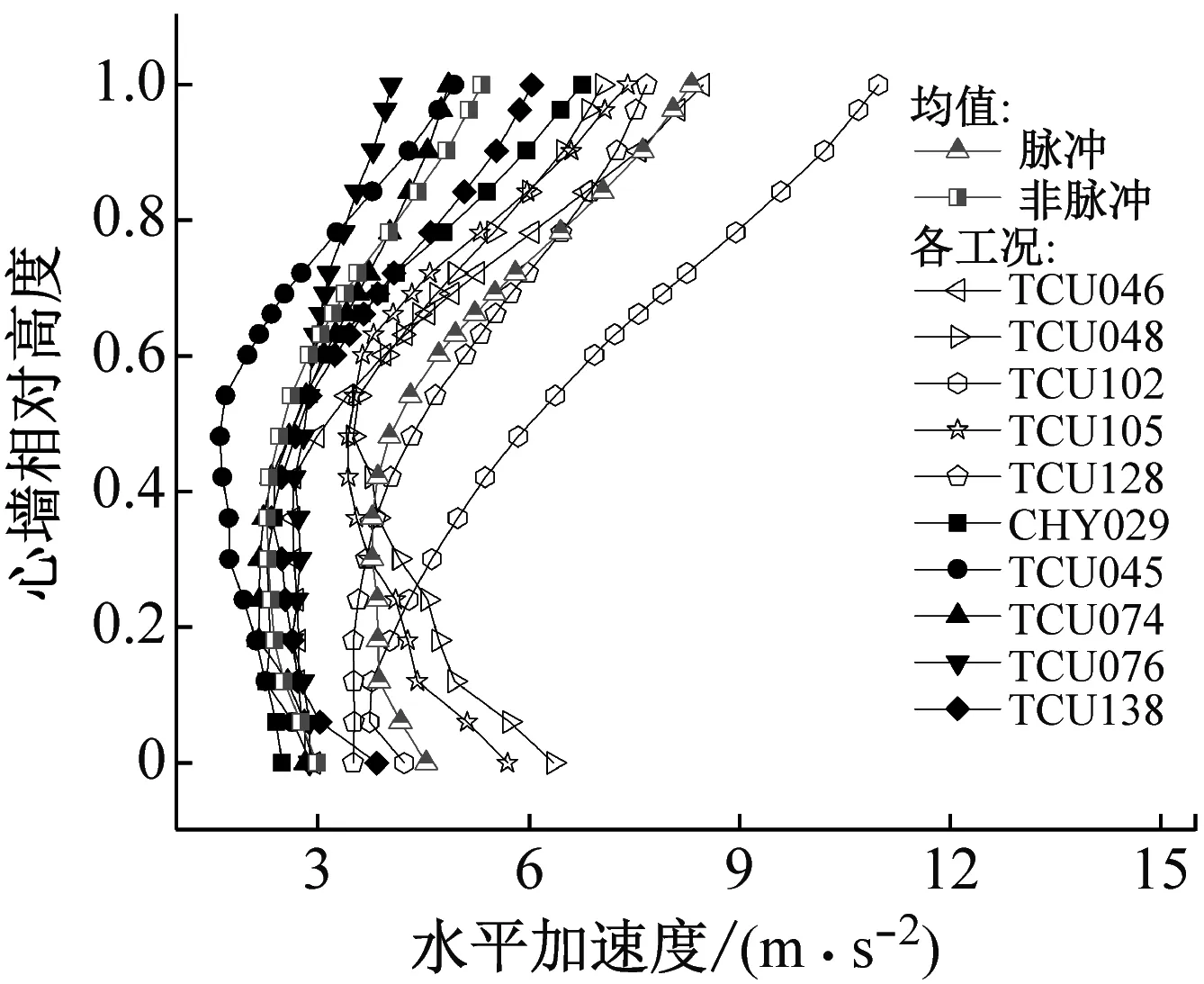
(a) 水平向加速度
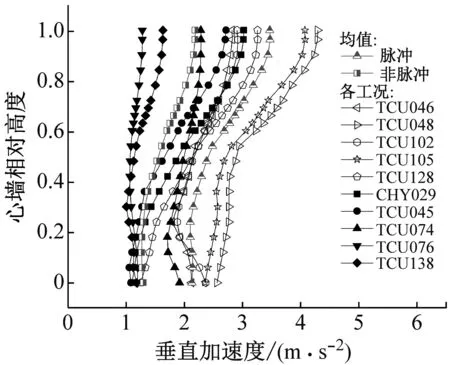
(b) 豎向加速度圖7 30度入射時(shí)心墻加速度沿墻高分布
對(duì)于角度變化引起的應(yīng)力極值變化,脈沖型地震動(dòng)比無(wú)脈沖型地震動(dòng)敏感,如15°到25°時(shí),脈沖型地震動(dòng)的豎向拉應(yīng)力均值變大了0.124 MPa,無(wú)脈沖型才變大了0.051 MPa。各工況下,心墻豎向拉應(yīng)力分布情況較為類(lèi)似,均分布在心墻底部靠上游側(cè)。
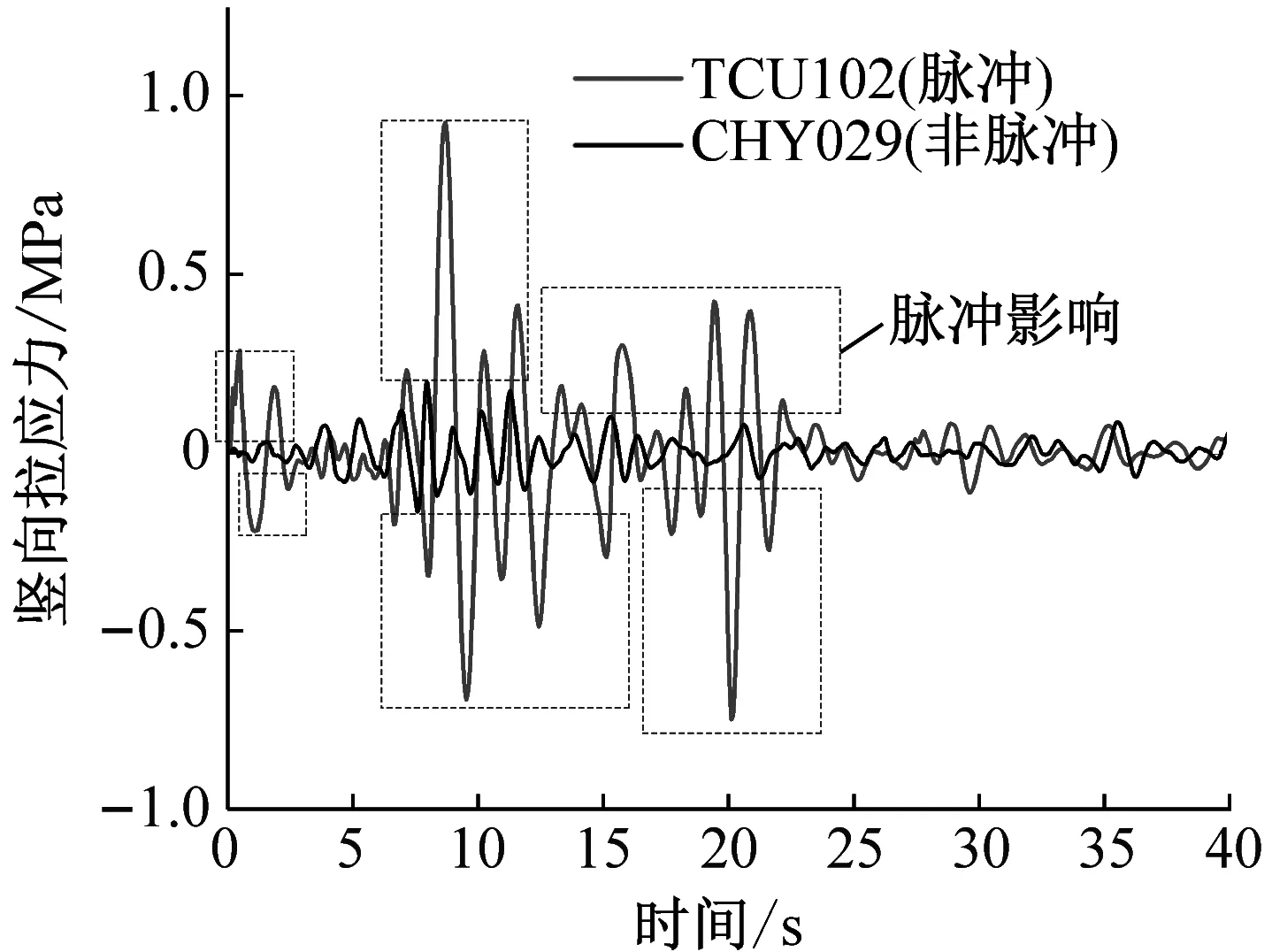
同一入射角度下脈沖地震動(dòng)和無(wú)脈沖地震動(dòng)作用的同一位置,心墻豎向應(yīng)力時(shí)程曲線規(guī)律隨輸入波的類(lèi)型不同存在差異;此差異可通過(guò)任一條脈沖地震動(dòng)和任一條無(wú)脈沖地震動(dòng)對(duì)比得出。因篇幅限制,圖8給出了0°和30°斜入射時(shí)脈沖和非脈沖SV波各1條下的心墻底部某點(diǎn)豎向應(yīng)力隨時(shí)間變化曲線,應(yīng)力拉為正,壓為負(fù)。由圖可見(jiàn),無(wú)論是垂直入射還是斜入射,脈沖型地震動(dòng)在地震開(kāi)始就給心墻帶來(lái)了較大的應(yīng)力,且在后續(xù)時(shí)間歷程中出現(xiàn)了比無(wú)脈沖型地震動(dòng)作用下時(shí)長(zhǎng)更長(zhǎng)、峰值更大的應(yīng)力,體現(xiàn)出明顯的脈沖效應(yīng)。
4.3 壩體永久變形
圖9為SV波不同入射角度下壩體水平向和豎向永久變形與PGV/PGA的關(guān)系圖。由圖可見(jiàn),在SV波斜入射下壩體永久變形以水平向?yàn)橹鳎较蚝拓Q向永久變形均隨PGV/PGA的增大而增大,水平向增大更為顯著。脈沖型地震動(dòng)選取的原則是PGV/PGA>0.2,這也說(shuō)明了脈沖型地震動(dòng)響應(yīng)大于無(wú)脈沖型的原因。
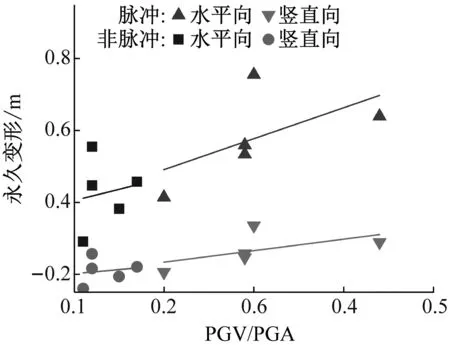
(a) 0°入射
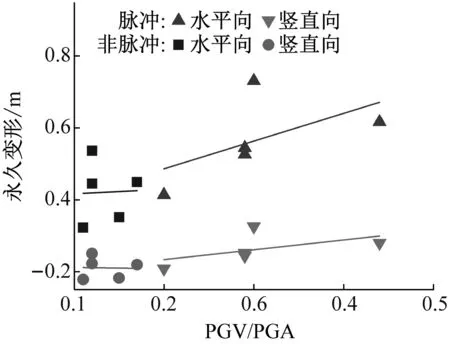
(c) 25°入射
壩體水平向、豎直向永久變形隨SV波入射角度的變化如圖10(a)和(b)所示,隨入射角度增加,壩體水平向、豎向永久變形均值呈先略減小后增大的趨勢(shì),這和心墻的加速度響應(yīng)隨入射角度變化的規(guī)律一致。
入射角度為30°時(shí)壩體的水平、豎向永久變形達(dá)到了最大值分別是:脈沖型地震動(dòng)均值為0.62 m、0.28 m,無(wú)脈沖型地震動(dòng)均值為0.46 m、0.22 m;脈沖型、無(wú)脈沖型地震動(dòng)的永久變形值在入射角度為15°和25°時(shí)相近。觀察SV波0°和30°斜入射時(shí)壩頂?shù)淖冃畏糯髨D(圖10(c)),可直觀得到:地震動(dòng)的脈沖特性對(duì)永久變形的影響顯著大于入射角度的影響。
5 結(jié) 論
本文選取了10 條近斷層脈沖型和無(wú)脈沖型地震動(dòng)記錄,推導(dǎo)了SV波斜入射時(shí)左、底和右邊界面均考慮完整波場(chǎng)分解方案的等效節(jié)點(diǎn)力計(jì)算公式,建立了瀝青混凝土心墻壩有限元模型,基于等效線性黏彈性模型和沈珠江殘余變形模型,研究了近斷層脈沖特性和斜入射角度對(duì)瀝青混凝土心墻加速度、心墻應(yīng)力和壩體永久變形的影響,得出了以下結(jié)論:
(1) 心墻頂水平向加速度峰值隨著入射角度的增大先略有減小后略有增加,但整體變化不大,豎向加速度對(duì)入射角增加較為顯著;各地震動(dòng)引起的墻頂加速度放大的鞭梢效應(yīng)明顯;30°斜入射下脈沖型地震動(dòng)引起的心墻頂水平和豎向放大系數(shù)最大分別為4.25和1.77,而無(wú)脈沖型引起的放大系數(shù)最大為2.73和1.12。

(a) 各工況下壩體水平向永久變形

(c) 壩體變形放大50倍輪廓圖圖10 SV波斜入射時(shí)壩體永久變形圖Fig.10 The permanent deformation diagram of the dam when SV wave is incident obliquely
(2) 脈沖型和無(wú)脈沖型地震動(dòng)產(chǎn)生的心墻底部豎向拉應(yīng)力均隨著入射角度的增加而增大,在30°時(shí)達(dá)到最大,脈沖型最大為0.681 MPa,無(wú)脈沖型最大為0.266 MPa;無(wú)論是垂直入射還是斜入射,脈沖型地震動(dòng)產(chǎn)生的豎向應(yīng)力均顯著大于無(wú)脈沖型地震動(dòng)結(jié)果;脈沖型地震動(dòng)在地震開(kāi)始就給心墻帶來(lái)了較大的應(yīng)力,且在后續(xù)時(shí)間歷程中出現(xiàn)了比無(wú)脈沖型時(shí)長(zhǎng)更長(zhǎng)、峰值更大的應(yīng)力,體現(xiàn)出明顯的脈沖效應(yīng)。
(3) SV波斜入射下壩體永久變形以水平向?yàn)橹鳎较蚝拓Q向永久變形均隨PGV/PGA的增大而增大,水平向增大更為顯著;隨入射角度增加,壩體水平向、豎向永久變形均值呈先略減小后增大的趨勢(shì);脈沖型地震動(dòng)30°斜入射時(shí)壩體的水平、豎向永久變形分別達(dá)到了0.62 m、0.28 m;地震動(dòng)的脈沖特性對(duì)永久變形的影響顯著大于斜入射角度的影響。

