基于隔振器荷載特征的非線性隔振器設(shè)計(jì)方法研究

杜香剛

(1.中國鐵道科學(xué)研究院集團(tuán)有限公司鐵道建筑研究所， 北京 100081；2.高速鐵路軌道技術(shù)國家重點(diǎn)實(shí)驗(yàn)室，北京 100081)

傳統(tǒng)的隔振器往往由于自身的固有頻率無法降到足夠低而難以實(shí)現(xiàn)期望的隔振目標(biāo)，主要體現(xiàn)在低頻隔振性能差，以及缺乏可調(diào)控性和自適應(yīng)能力等方面[1-2]。高承載能力和低固有頻率之間的矛盾成為被動(dòng)隔振技術(shù)發(fā)展的瓶頸，低頻隔振尤其是重型設(shè)備的低頻隔振也一直是被動(dòng)隔振的難點(diǎn)問題[3-4]。

隨著我國城市化進(jìn)程加快，地鐵引起的環(huán)境振動(dòng)問題越來越受到人們的重視，因此，在地鐵軌道設(shè)計(jì)時(shí)采用了多型減振措施。在眾多軌道減振措施中，鋼彈簧浮置板軌道被認(rèn)為是減振效果最好的減振軌道形式。經(jīng)大量測試，鋼彈簧浮置板軌道能夠有效抑制高頻振動(dòng)，但對(duì)低頻振動(dòng)抑制效果并不明顯，特別是對(duì)于實(shí)驗(yàn)室、博物館等建筑物內(nèi)精密儀器和珍貴文物十分敏感的10 Hz左右振動(dòng)成分難以達(dá)到理想的衰減效果。

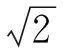
隨著振動(dòng)控制要求的不斷提高，基于非線性理論的隔振技術(shù)的研究和應(yīng)用越發(fā)廣泛[9-11]，非線性系統(tǒng)可以通過自身阻尼非線性和剛度非線性來改善系統(tǒng)本身的隔振性能[12-14]。非線性隔振技術(shù)可以根據(jù)系統(tǒng)激勵(lì)及振動(dòng)特點(diǎn)進(jìn)行最優(yōu)參數(shù)設(shè)計(jì)，因此，利用非線性被動(dòng)隔振技術(shù)解決既有線性隔振系統(tǒng)存在的問題是城市軌道交通減振軌道設(shè)計(jì)的重要方向。一種名為SD振子的非線性系統(tǒng)于2006年被曹慶杰教授所提出，這類系統(tǒng)由一個(gè)被一對(duì)斜拉彈簧所約束的質(zhì)量塊構(gòu)成。研究表明，SD振子是一種典型的幾何非線性特征的非線性系統(tǒng)，大量學(xué)者對(duì)SD振子的豐富的動(dòng)力學(xué)行為進(jìn)行了詳細(xì)的研究，同時(shí)由于其幾何參數(shù)的可調(diào)性，可以廣泛應(yīng)用于低頻、超低頻隔振等工程領(lǐng)域，朱光楠等對(duì)SD振子系統(tǒng)在變壓器抗震領(lǐng)域的應(yīng)用進(jìn)行了系統(tǒng)、詳細(xì)的理論以及試驗(yàn)研究。

本文基于非線性隔振理論，在隔振器荷載特征分析的基礎(chǔ)上，提出了基于隔振器荷載特征的非線性隔振器設(shè)計(jì)方法，對(duì)隔振器的剛度和阻尼曲線進(jìn)行非線性設(shè)計(jì)優(yōu)化，使得隔振器同時(shí)具有良好的低頻隔振性能和振動(dòng)位移控制能力。

1 基于隔振器荷載特征的非線性隔振器設(shè)計(jì)流程

傳統(tǒng)浮置板軌道的設(shè)計(jì)方法是以線性隔振理論為基礎(chǔ)的設(shè)計(jì)方法，即根據(jù)環(huán)評(píng)要求和地鐵設(shè)計(jì)相關(guān)規(guī)范，設(shè)計(jì)具有滿足規(guī)范要求和施工要求的浮置板軌道的固有頻率及隔振器剛度，以經(jīng)驗(yàn)為基礎(chǔ)確定浮置板軌道的基本結(jié)構(gòu)尺寸及隔振器的初步布置方式；在此基礎(chǔ)上根據(jù)車輛軸重、軸距等信息對(duì)浮置板的結(jié)構(gòu)及隔振器的剛度及布置方式進(jìn)行校核。傳統(tǒng)設(shè)計(jì)方法往往只針對(duì)系統(tǒng)的減振性能進(jìn)行設(shè)計(jì)而無法兼顧輪軌系統(tǒng)的動(dòng)力學(xué)行為，更無法考慮輪軌動(dòng)態(tài)激勵(lì)引起的隔振器荷載特征，因此導(dǎo)致了浮置板軌道在實(shí)際使用中存在對(duì)低頻隔振性能差和輪軌系統(tǒng)振動(dòng)響應(yīng)大等問題。

鑒于以上原因，本文提出了基于隔振器荷載特征的非線性浮置板減振軌道系統(tǒng)的設(shè)計(jì)方法(如圖1所示)，首先建立車輛-軌道-隧道系統(tǒng)動(dòng)力學(xué)模型(模型經(jīng)過實(shí)測數(shù)據(jù)修正)進(jìn)行系統(tǒng)動(dòng)力學(xué)分析計(jì)算，在對(duì)隔振器荷載特征識(shí)別的基礎(chǔ)上，運(yùn)用非線性動(dòng)力學(xué)優(yōu)化模型進(jìn)行浮置板非線性隔振器的剛度及阻尼曲線優(yōu)化設(shè)計(jì)，最后將優(yōu)化得到的非線性特征曲線帶入車輛-軌道-隧道動(dòng)力學(xué)模型進(jìn)行分析驗(yàn)證。

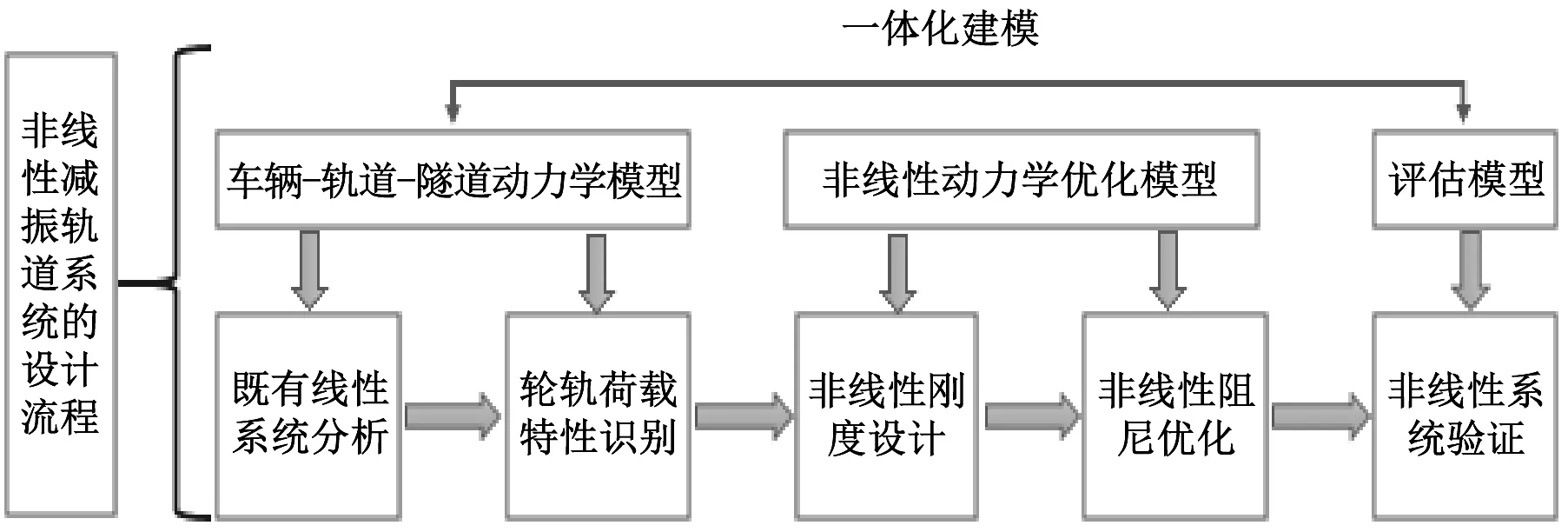
圖1 基于隔振器荷載特征的非線性隔振器設(shè)計(jì)流程

2 車輛-軌道-隧道耦合動(dòng)力學(xué)模型

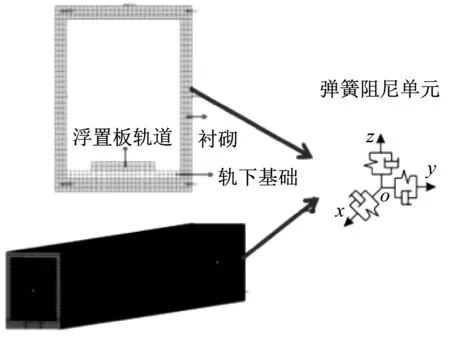
建立車輛-軌道-隧道耦合動(dòng)力學(xué)模型獲取隔振器荷載，并對(duì)設(shè)計(jì)的非線性特征曲線進(jìn)行分析驗(yàn)證是本文設(shè)計(jì)方法的基礎(chǔ)。因此，該模型需包含列車模型、浮置板軌道模型、隧道模型及輪軌接觸模型，可以將鋼彈簧設(shè)計(jì)為非線性曲線來模擬非線性隔振器。以某地鐵線路的浮置板軌道為例(如圖2所示)，根據(jù)某B型地鐵車輛及軌道和隧道的動(dòng)力學(xué)參數(shù)(如表1所示)建立如圖3所示的車輛-浮置板軌道-隧道系統(tǒng)一體化仿真分析模型，其中車輛系統(tǒng)主要由車體、轉(zhuǎn)向架、輪對(duì)和一系、二系懸掛組成。對(duì)車輛模擬時(shí)，將車輛的基本部件近似處理為剛體，各基本部件之間通過彈性或剛性約束來限制車輛結(jié)構(gòu)中各部件間的相對(duì)運(yùn)動(dòng)。模型中浮置板軌道系統(tǒng)由鋼軌、扣件、軌道板及鋼彈簧組成，其中軌道板采用實(shí)體單元建模，鋼軌采用鐵木辛柯梁模擬，扣件采用彈簧阻尼單元進(jìn)行模擬，鋼彈簧采用非線性彈簧力元。軌道設(shè)置為：普通整體道床+5段25 m長浮置板道床+普通整體道床，建立浮置板軌道時(shí)既考慮了板與板之間起連接作用的剪力鉸，又考慮浮置板間鋼彈簧的局部加密情況(如圖4所示)。為了能夠反映相鄰車輛轉(zhuǎn)向架對(duì)浮置板以及鋼軌動(dòng)態(tài)下沉量和扣件力的影響，本文采用三車模型進(jìn)行仿真模擬。輪軌接觸采用UM柔性軌道模塊中自帶的Kik-Piotrowski多點(diǎn)非赫茲接觸模型來計(jì)算輪軌蠕滑力，該模型可以考慮車輪和鋼軌的微小穿透，法向壓力分布沿前進(jìn)方向呈橢圓形狀，切向接觸斑形狀為非橢圓。模型中地基和隧道結(jié)構(gòu)采用實(shí)體單元模擬，由于有限元模型只能在有限范圍內(nèi)求解振動(dòng)的傳播問題，由于主體的實(shí)際情況是無邊界的形式，因此在模型截取的界面上會(huì)發(fā)生波的反射，導(dǎo)致模型結(jié)果失真，因此本模型采用低反射邊界，在模型邊界的節(jié)點(diǎn)上的法向和切向設(shè)置彈簧阻尼元件來模擬無限范圍對(duì)計(jì)算范圍的效果。模型的仿真結(jié)果經(jīng)過與實(shí)測數(shù)據(jù)進(jìn)行對(duì)比修正后[15]，取列車的運(yùn)行速度為80 m/h的隔振器支反力作非線性系統(tǒng)的設(shè)計(jì)輸入。

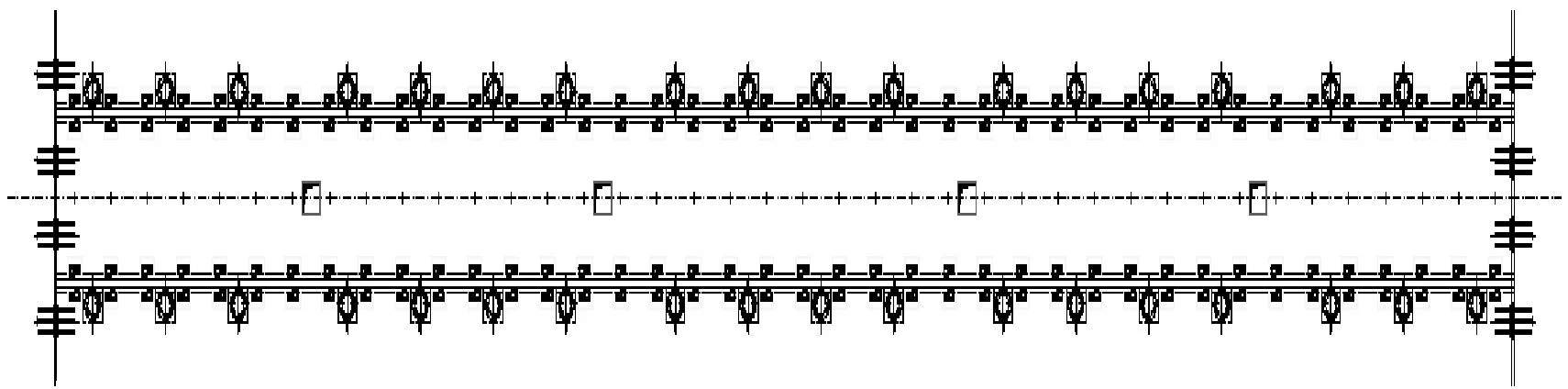
(a) 縱向布置圖

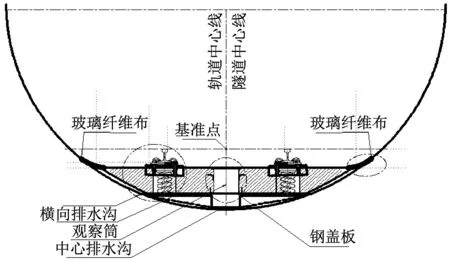
(b) 斷面結(jié)構(gòu)圖圖2 浮置板軌道結(jié)構(gòu)圖Fig.2 Structure graphing of floating slab system

表1 建模基本參數(shù)Tab.1 Basic parameters of modeling

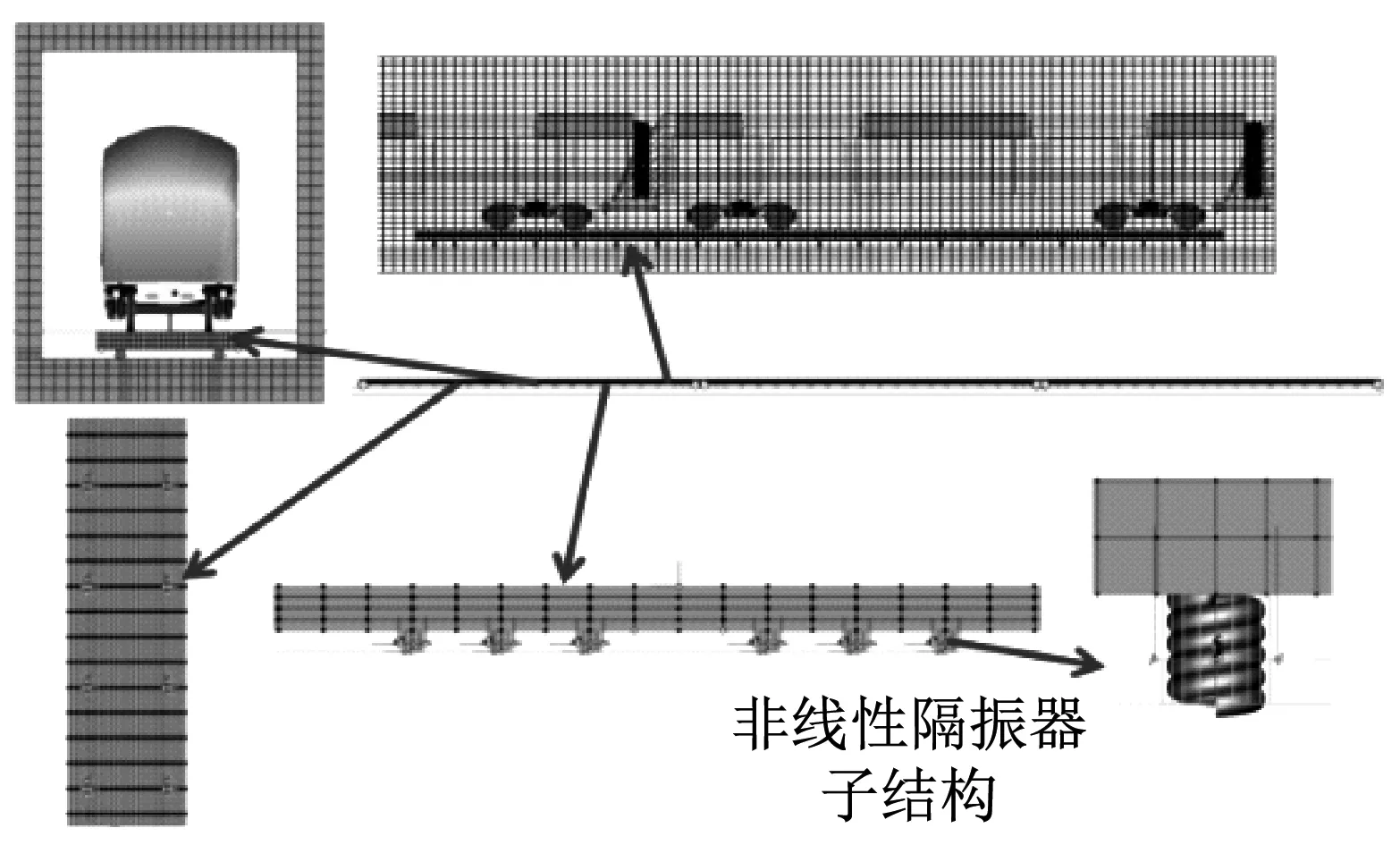
(a) 一體化仿真模型

(b) 隧道模型圖3 車輛-軌道-隧道一體化仿真模型Fig.3 The system dynamic model

(b) 正視圖圖4 車輛-浮置板軌道耦合動(dòng)力學(xué)仿真分析模型Fig.4 Vehicle-floating slab track system couplingdynamic simulation model

3 浮置板軌道用隔振器荷載特征識(shí)別

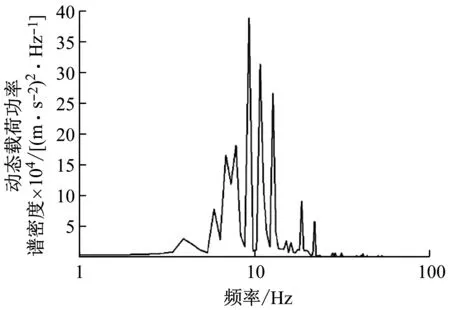
根據(jù)第2章建立的模型，提取中間板端部、中部和尾部隔振器的垂向荷載時(shí)間歷程(如圖5所示)，由圖可知浮置板中部隔振器受力最大，端部和尾部隔振器受力相對(duì)較小，這是由于浮置板中部板的柔性較大，端部和尾部隔振器間距較小的原因。因此在后續(xù)分析中，以受力最大的中部隔振器作為研究對(duì)象。對(duì)板中部隔振器荷載曲線進(jìn)行頻譜分析，如圖6所示，可以看到隔振器荷載分為準(zhǔn)靜態(tài)沖擊荷載部分(4 Hz以下，移動(dòng)質(zhì)量引起的沖擊荷載，以下簡稱沖擊荷載)與動(dòng)態(tài)荷載(4 Hz以上，以下簡稱動(dòng)態(tài)荷載)，且沖擊荷載要遠(yuǎn)大于動(dòng)態(tài)荷載，沖擊荷載主要影響浮置板位移，而動(dòng)態(tài)荷載主要影響環(huán)境振動(dòng)。

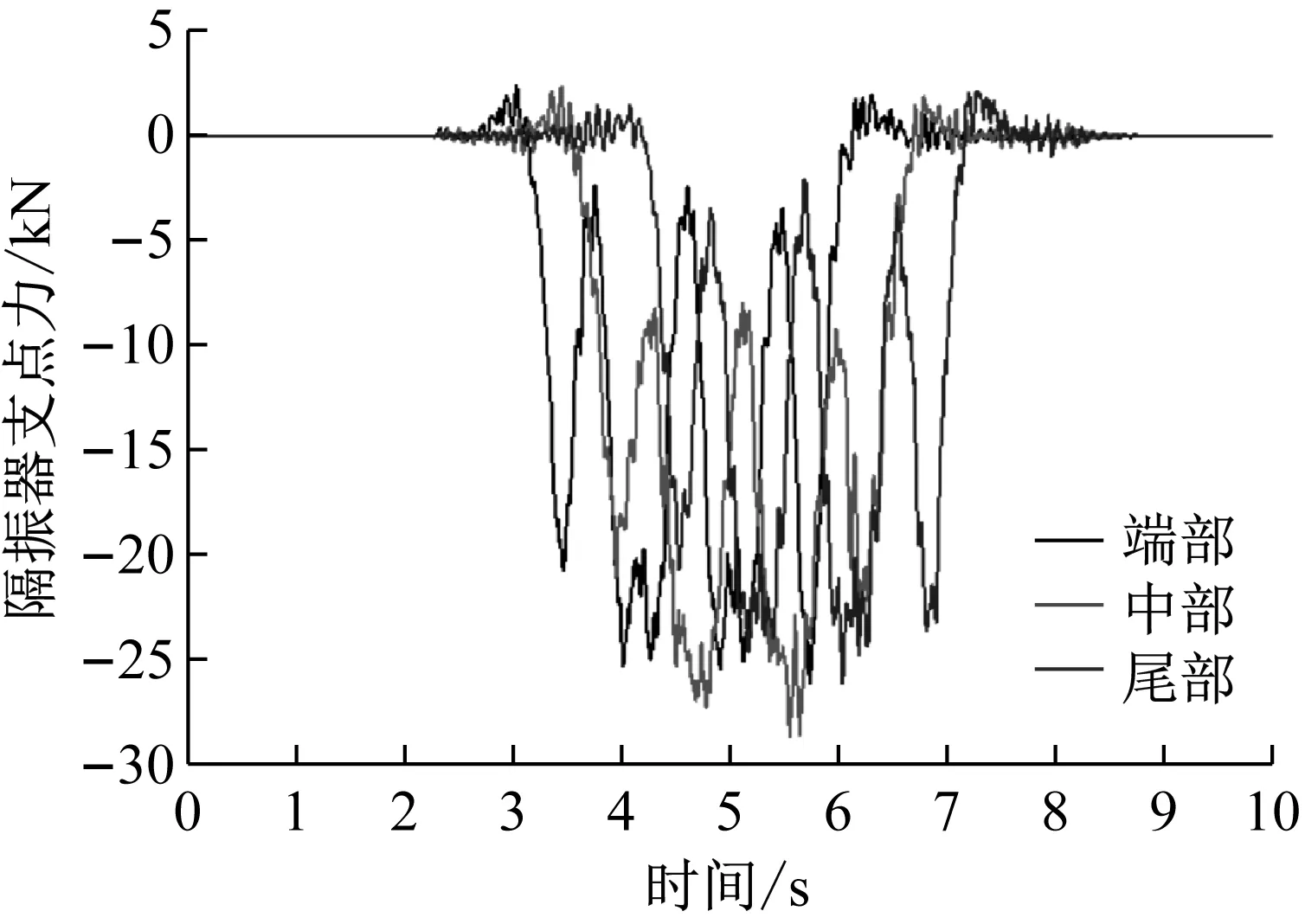
圖5 隔振器垂向荷載Fig.5 Vertical loads of floating slab isolators

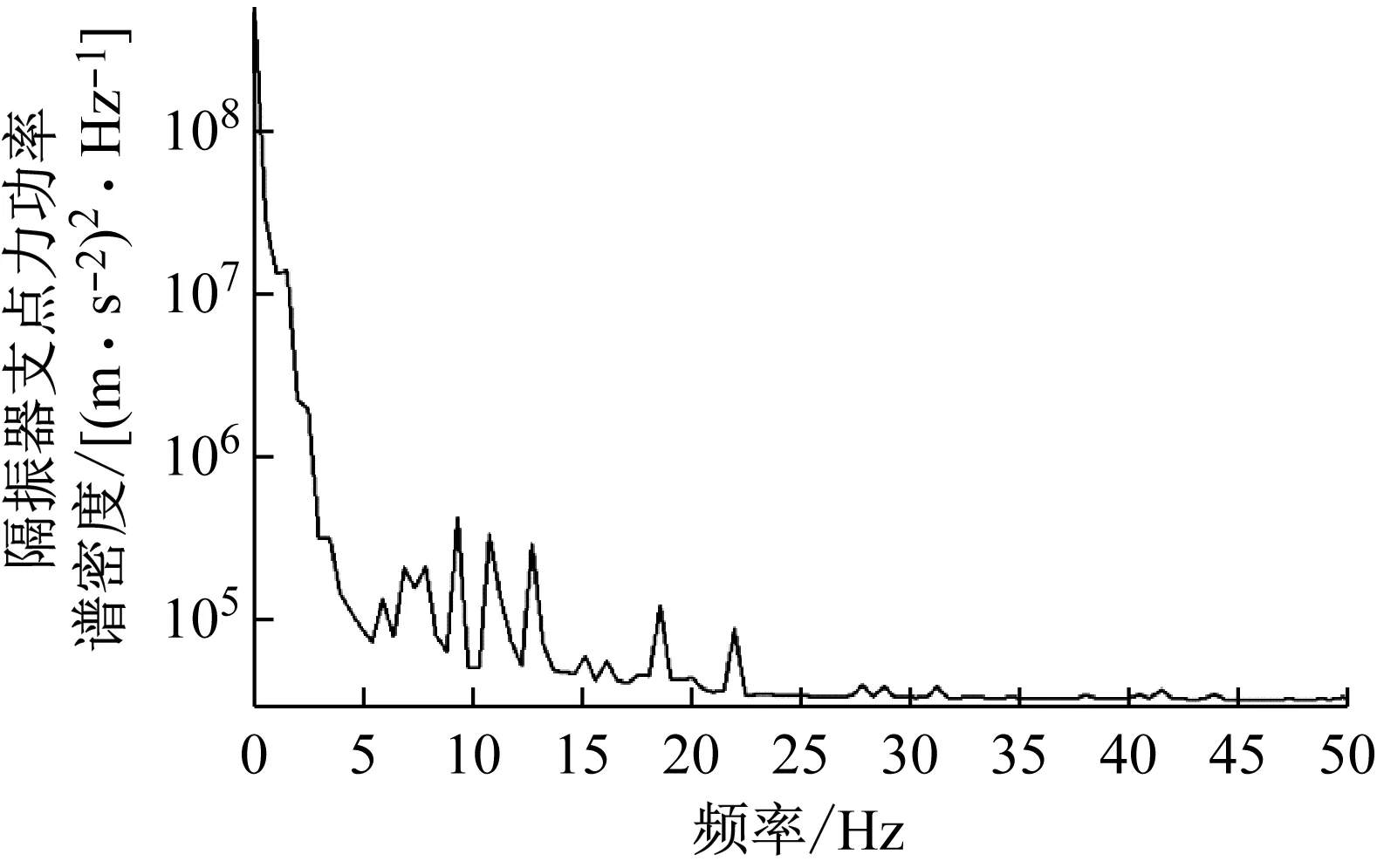
圖6 板中隔振器荷載功率譜密度圖Fig.6 PSD diagram of isolator loads in themiddle of floating slab

準(zhǔn)確地提出非線性浮置板軌道系統(tǒng)的控制及優(yōu)化目標(biāo)是非線性浮置板軌道隔振器參數(shù)設(shè)計(jì)的關(guān)鍵，因此需要結(jié)合列車經(jīng)過浮置板軌道的動(dòng)態(tài)過程對(duì)隔振器荷載的特征進(jìn)行分析。圖7為列車經(jīng)過浮置板軌道的全過程，從圖中可以看出，在靜平衡位置處(分別對(duì)應(yīng)列車開始駛?cè)牒蛣傫偝龈≈冒?的隔振器荷載的振蕩為隔振器未受到列車沖擊荷載時(shí)的自由振動(dòng)；當(dāng)列車進(jìn)入浮置板軌道時(shí)，在沖擊荷載上疊加有動(dòng)態(tài)的隨機(jī)振動(dòng)荷載。非線性隔振器的設(shè)計(jì)需要同時(shí)考慮浮置板的位移控制與振動(dòng)控制，因此，需將隔振器荷載按照沖擊荷載與動(dòng)態(tài)荷載進(jìn)行分解，如圖7所示。從圖中看到，隔振器沖擊荷載呈現(xiàn)4個(gè)峰(谷)值，P1為兩節(jié)車相鄰轉(zhuǎn)向架引起的荷載最小值；P2為頭尾轉(zhuǎn)向架引起的荷載最小值；P3為頭尾轉(zhuǎn)向架作用于隔振器上的最大荷載，P4為兩節(jié)車相鄰轉(zhuǎn)向架作用于隔振器上的最大荷載，如表2所示。表2中AW0為空載工況，AW2為正常荷載工況，AW3為滿載工況。從圖7(b)可以看出，動(dòng)態(tài)荷載的振動(dòng)能量主要集中在10 Hz附近。

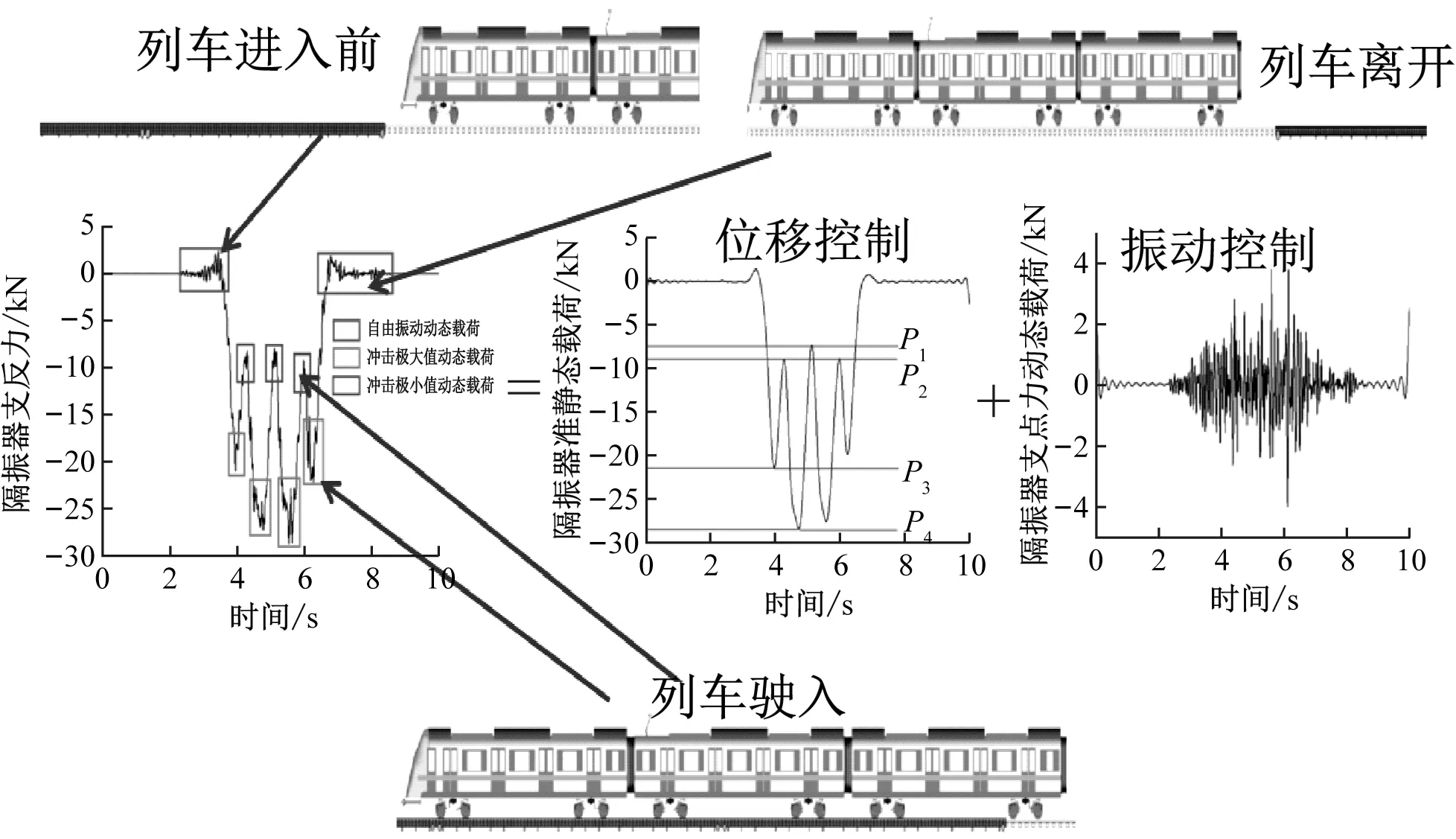
(a)

(b)圖7 隔振器荷載特征分析圖Fig.7 Floating slab isolator loads characteristics analysis

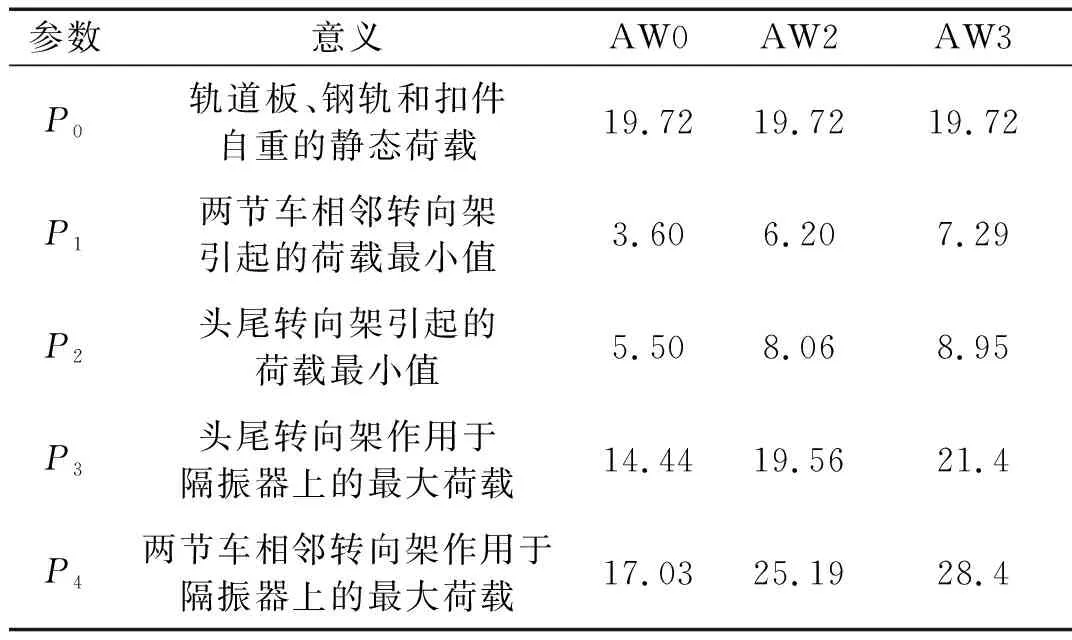
表2 不同工況下隔振器沖擊荷載極值Tab.2 Extreme value of isolator shock loads under different working conditions kN

因此，基于以上隔振器荷載動(dòng)態(tài)特征，定性判斷所構(gòu)造的非線性剛度曲線應(yīng)保證系統(tǒng)在靜平衡位置處(即車輛駛來浮置板前及車輛駛離浮置板后)和沖擊荷載的極值位置處具有較好的隔振效果，同時(shí)抑制車輛駛來和離開后浮置板的自由振蕩以及沖擊動(dòng)荷載引起的振蕩。為保證系統(tǒng)具有足夠的儲(chǔ)能能力，令系統(tǒng)的大剛度區(qū)間盡可能發(fā)生在無明顯振蕩區(qū)域，且令系統(tǒng)最大剛度值在保證儲(chǔ)能能力的前提下盡可能小。

4 非線性隔振器剛度曲線優(yōu)化設(shè)計(jì)

4.1 非線性動(dòng)力學(xué)優(yōu)化模型

本文基于SD振子幾何非線性隔振理論，根據(jù)實(shí)際設(shè)計(jì)需求和目標(biāo)構(gòu)造非線性動(dòng)力學(xué)方程，進(jìn)而獲得滿足實(shí)際情況的最優(yōu)設(shè)計(jì)參數(shù)，并依據(jù)設(shè)計(jì)參數(shù)選擇滿足設(shè)計(jì)參數(shù)要求的最優(yōu)結(jié)構(gòu)形式。建立的單隔振器力學(xué)模型如圖8所示，圖中振子m在豎直方向振動(dòng)，其通過承載彈簧和阻尼與基礎(chǔ)相連，垂直彈簧為系統(tǒng)提供正向承載力。水平彈簧-連桿機(jī)構(gòu)為系統(tǒng)提供負(fù)剛度，連桿一端與質(zhì)量為m的振子鉸接，另一端鉸接于水平放置的彈簧，彈簧末端與基礎(chǔ)相連。水平彈簧的剛度為k1，豎向彈簧剛度為k0，阻尼為C，非線性系統(tǒng)的初始平衡位移距離水平彈簧的高度為d，連桿長度為l，彈簧原長為L，水平彈簧原長末端到振子中心的水平距離為B。正常工作狀態(tài)下，豎向彈簧k0處于預(yù)壓縮狀態(tài)來承載浮置板和列車的重力荷載，水平彈簧k1處于預(yù)壓縮狀態(tài)保證彈簧-連桿機(jī)構(gòu)為系統(tǒng)提供負(fù)剛度，使得正負(fù)剛度并聯(lián)在振動(dòng)范圍內(nèi)形成非線性剛度，從而達(dá)到低頻隔振的目的。

肝龍膠囊對(duì)豬血清誘導(dǎo)的肝纖維化大鼠的治療作用……李 燕，邵明園，國 超，楊強(qiáng)麗，曹昌娥，賴 泳（13）

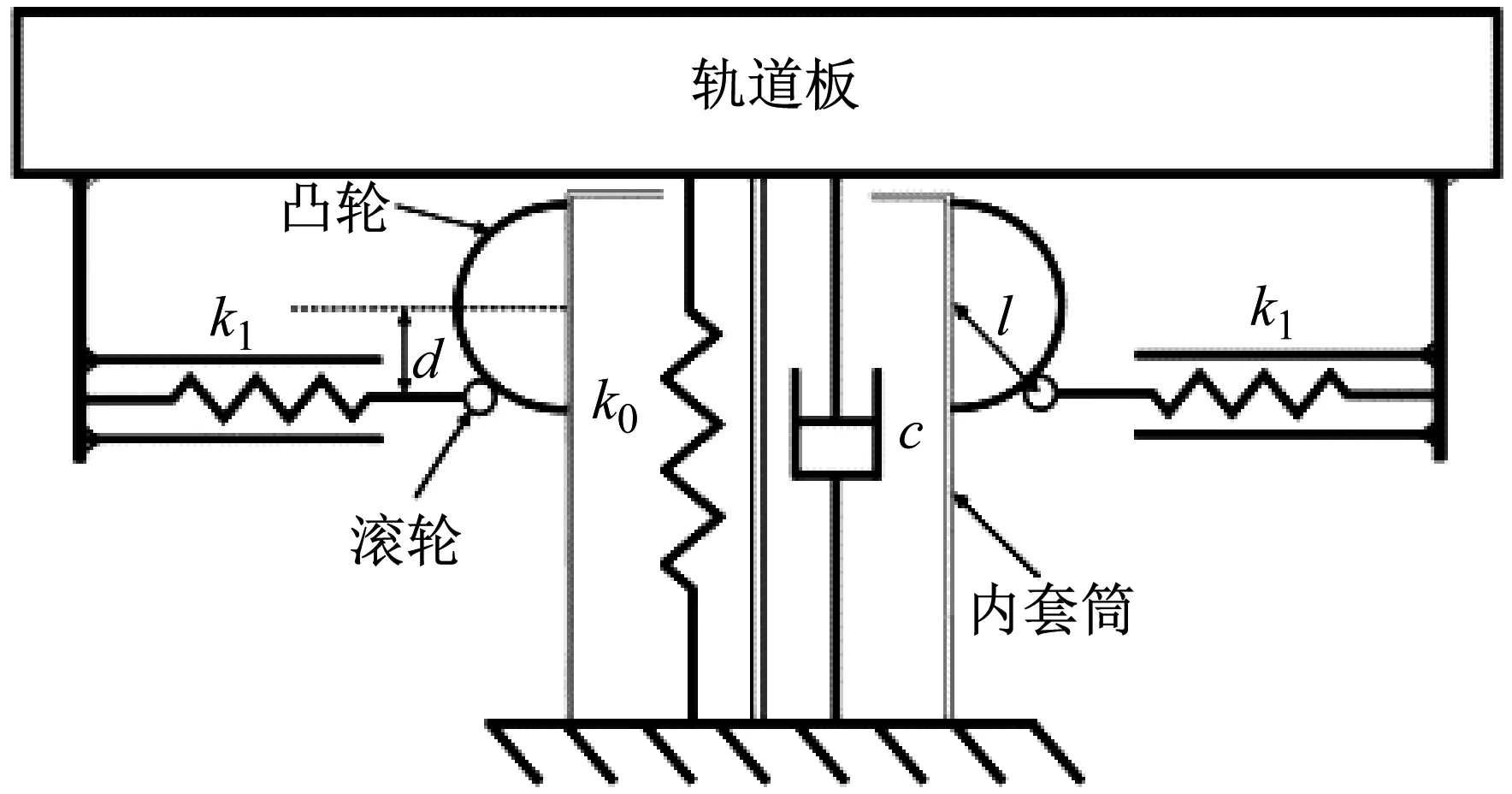
圖8 浮置板-非線性隔振器示意圖Fig.8 Vibration isolator physical model

圖8所示的非線性動(dòng)力學(xué)方程為式(1)，基于該動(dòng)力學(xué)方程，根據(jù)優(yōu)化目標(biāo)進(jìn)行非線性剛度曲線的設(shè)計(jì)。

(1)

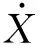
4.2 隔振器非線性剛度曲線設(shè)計(jì)方法

圖9所示為非線性隔振器剛度曲線設(shè)計(jì)原理示意圖，圖中虛線表示傳統(tǒng)鋼彈簧隔振器剛度曲線示意圖，紅線表示非線性隔振器剛度曲線示意圖。根據(jù)實(shí)際工程設(shè)計(jì)需求，分別按照起始隔振頻率控制需求、振動(dòng)位移控制需求和振動(dòng)衰減速度控制需求三方面對(duì)非線性隔振曲線進(jìn)行設(shè)計(jì)。

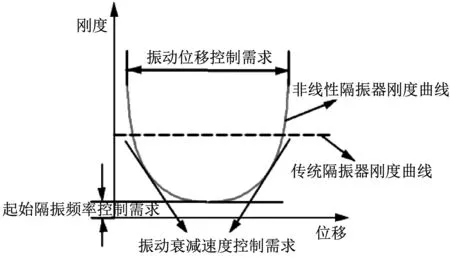
圖9 非線性隔振器剛度曲線設(shè)計(jì)原理圖Fig.9 Schematic diagram of nonlinear isolator stiffness curve

根據(jù)第1章的分析，隔振器的支反力響應(yīng)可以被分解為沖擊響應(yīng)和隨機(jī)響應(yīng)兩部分。其中沖擊響應(yīng)部分可視為由車輛駛?cè)雽?dǎo)致隔振系統(tǒng)荷載質(zhì)量變化引起的具有振幅大、頻率低的響應(yīng)；而隨機(jī)響應(yīng)部分則可以視為由輪軌接觸引發(fā)的具有振幅小、頻率高的響應(yīng)。

為保證車輛行駛的平穩(wěn)性，以及對(duì)隔振系統(tǒng)的隔振性能的要求，需同時(shí)保證車輛加載至浮置板上后浮置板的振動(dòng)位移不可過大，以及隔振器向地基所傳遞的能量相比線性系統(tǒng)有所衰減。利用4.1節(jié)介紹的力學(xué)模型，設(shè)置非線性剛度曲線的優(yōu)化指標(biāo)：浮置板振動(dòng)位移峰峰值不超過3 mm；浮置板隔振系統(tǒng)通過隔振器傳遞至地基的振動(dòng)能量，在低頻段(≤20 Hz)相比線性系統(tǒng)存在明顯衰減效果；在隔振器荷載強(qiáng)度大的位置處系統(tǒng)相比線性系統(tǒng)存在明顯的衰減效果。

考慮到車輛自重不變，可以視為車輛駛?cè)霑r(shí)向隔振系統(tǒng)輸入一固定的準(zhǔn)靜態(tài)力，進(jìn)而應(yīng)使隔振系統(tǒng)在受到車輛準(zhǔn)靜態(tài)作用后，進(jìn)入隔振區(qū)段。因此對(duì)于隔振器進(jìn)入隔振區(qū)間的位置可根據(jù)P0、P1、P2、P3以及P4點(diǎn)的發(fā)生位置進(jìn)行確定，上述各個(gè)荷載值所對(duì)應(yīng)的位移分別被稱為X0、X1、X2、X3以及X4，從而提升系統(tǒng)對(duì)隨機(jī)振動(dòng)部分的抑制能力。簡言之，基于系統(tǒng)沖擊響應(yīng)部分特征決定荷載位移的控制能力，而基于對(duì)隨機(jī)響應(yīng)部分特征決定隔振器的隔振能力。

因此通過結(jié)合荷載分析結(jié)果，考慮設(shè)計(jì)一種非線性隔振器，旨在保證在系統(tǒng)具有對(duì)浮置板足夠的承載能力；以及在空載至準(zhǔn)靜態(tài)荷載之間具有足夠的等效剛度抑制響應(yīng)位移；同時(shí)保證系統(tǒng)在隨機(jī)荷載集中的位置附近具有較高的隔振性能。因此，根據(jù)隔振器荷載特征，基于如圖8所示的模型所具有的結(jié)構(gòu)參數(shù)，通過大量仿真計(jì)算優(yōu)化設(shè)計(jì)見圖10線性隔振器恢復(fù)力-位移曲線和圖11非線性隔振器恢復(fù)力-位移曲線。

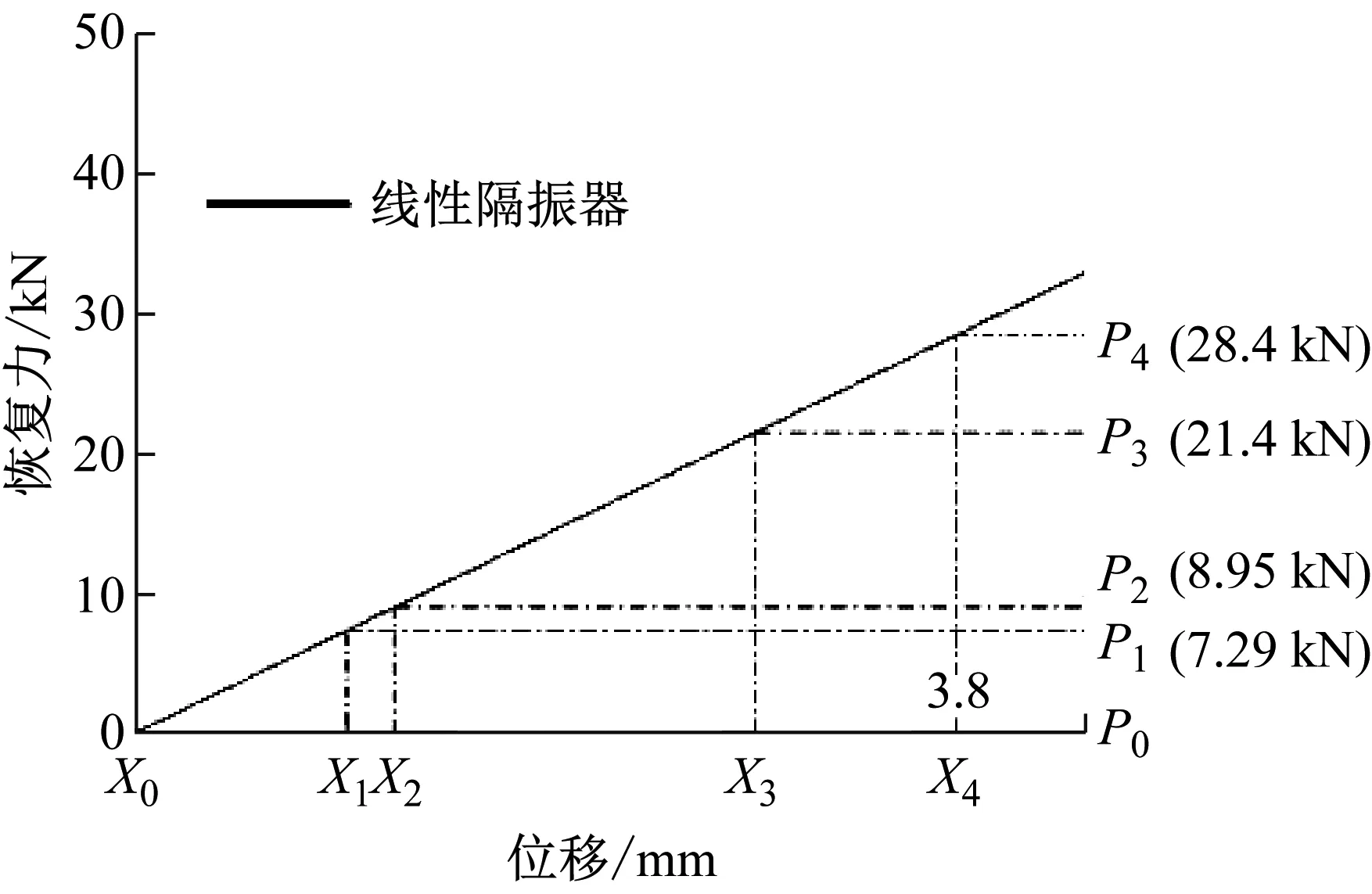
圖10 線性隔振器恢復(fù)力-位移曲線圖Fig.10 Linear force-displacement curve

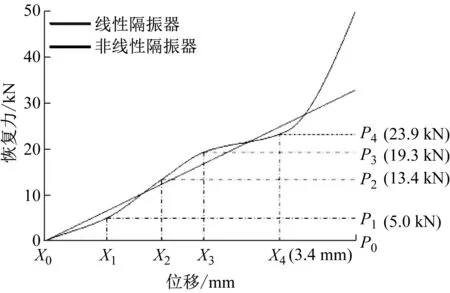
圖11 非線性隔振器恢復(fù)力-位移曲線圖Fig.11 Nonlinear force-displacement curve

將非線性隔振器恢復(fù)力曲線代入圖3所示的車輛-軌道-隧道耦合動(dòng)力學(xué)模型，得到圖12(a)浮置板振動(dòng)位移響應(yīng)曲線圖，從圖中可以看出，非線性隔振系統(tǒng)相比原有線性系統(tǒng)的浮置板動(dòng)態(tài)位移具有明顯的抑制效果，最大動(dòng)態(tài)位移減小約20%左右；圖12(b)為非線性隔振系統(tǒng)在車輛運(yùn)行時(shí)引起的隔振器支反力響應(yīng)曲線。從圖中可以看出，相比原有線性系統(tǒng)在荷載位置P0以及在和位置P3、P4處響應(yīng)具有明顯的抑制效果；圖12(c)為隔振器支反力響應(yīng)的功率譜密度曲線的對(duì)比圖，從圖中看出，非線性隔振系統(tǒng)同時(shí)在低頻和高頻上產(chǎn)生了明顯的振動(dòng)隔離能力，進(jìn)而相比線性系統(tǒng)在幾乎全頻段上均體現(xiàn)出振動(dòng)的衰減效果。

5 非線性隔振器阻尼曲線優(yōu)化設(shè)計(jì)

在工程中常會(huì)有一些不規(guī)則的沖擊和振動(dòng)，因而適當(dāng)增大鋼彈簧隔振器阻尼可以抑制系統(tǒng)在這種沖擊和振動(dòng)作用下的振幅，并使自由振動(dòng)很快消失，尤其當(dāng)系統(tǒng)發(fā)生共振時(shí)，可以極大程度的抑制共振頻率處的響應(yīng)。但對(duì)于傳統(tǒng)線性黏性阻尼來說，增大阻尼雖然可以減小共振頻率下的響應(yīng)，但會(huì)降低隔振區(qū)的隔振效率。因此，本章基于隔振器荷載特征，設(shè)計(jì)隔振器非線性阻尼曲線，使得阻尼在減小共振峰值的同時(shí)不放大高頻荷載的振動(dòng)傳遞。

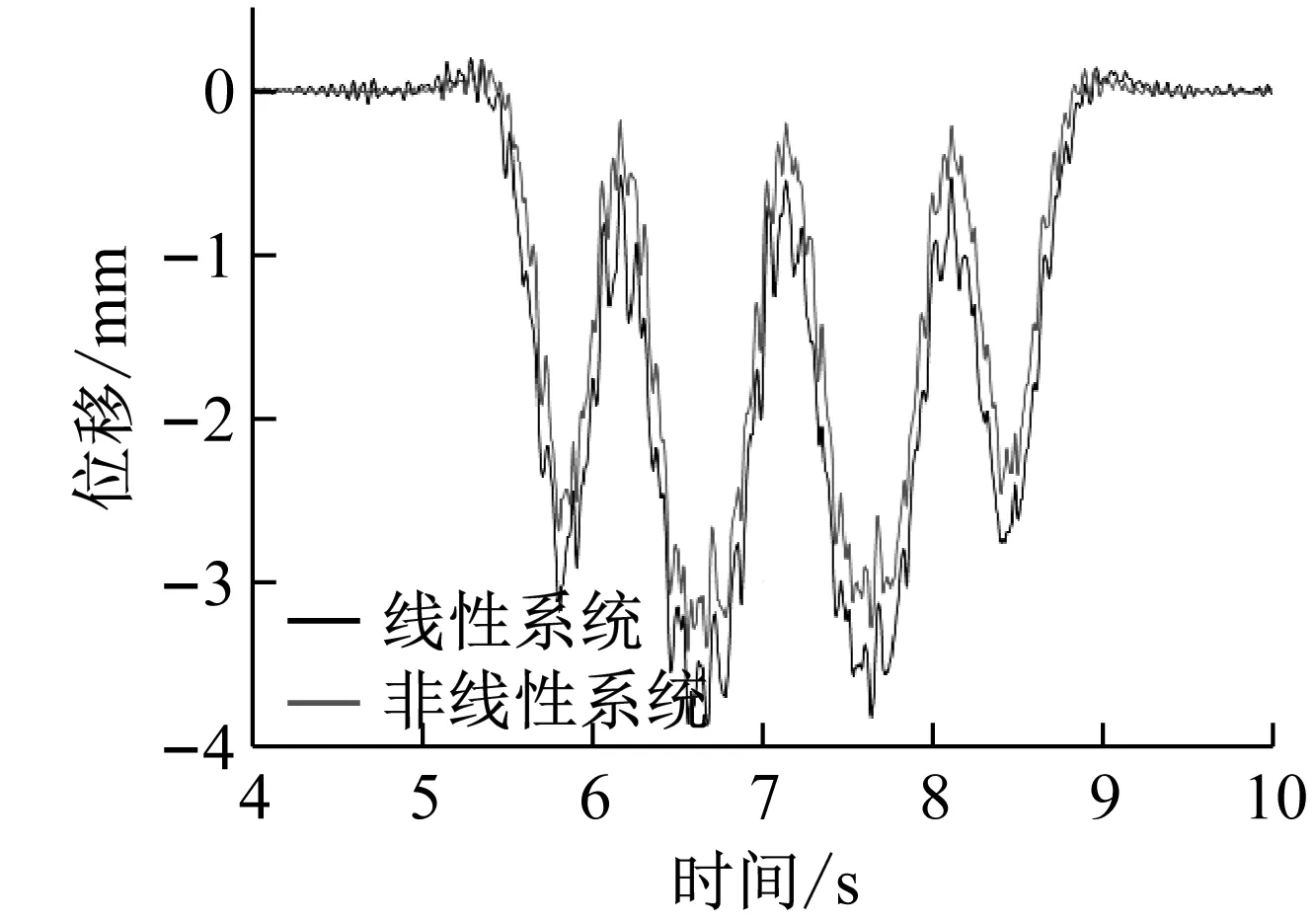
(a) 浮置板位移動(dòng)態(tài)響應(yīng)曲線圖

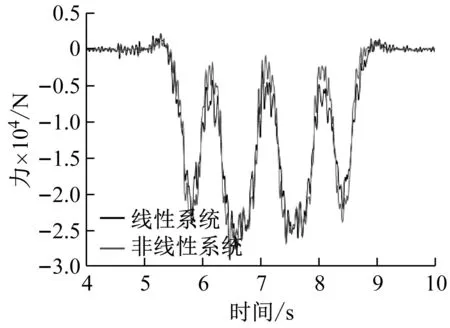
(b) 隔振器支反力動(dòng)態(tài)響應(yīng)曲線圖

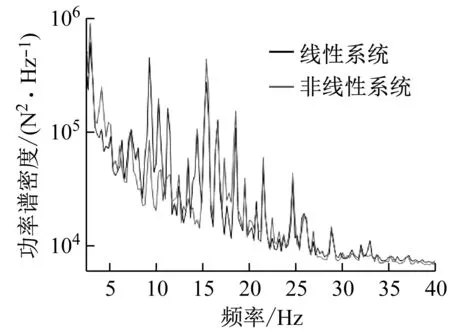
(c) 隔振器支反力響應(yīng)功率譜密度曲線對(duì)比圖圖12 非線性隔振系統(tǒng)效果對(duì)比圖Fig.12 Response diagrams of nonlinear isolator andtraditional isolator system

由2.2節(jié)分析結(jié)果可知，優(yōu)化出的非線性剛度隔振器在P1、P2位置處存在振動(dòng)放大現(xiàn)象。因此在本節(jié)在最優(yōu)剛度曲線的基礎(chǔ)上，設(shè)計(jì)隔振器最優(yōu)阻尼曲線，進(jìn)一步提高非線性隔振器性能。在第3節(jié)荷載分析的基礎(chǔ)上，分別設(shè)計(jì)4種非線性阻尼曲線(阻尼系數(shù)隨位移非線性變化)，分別是漸小非線性阻尼曲線、漸大分線性阻尼曲線、先大后小非線性阻尼曲線和先小后大非線性阻尼曲線(如圖13所示)，通過系統(tǒng)動(dòng)力學(xué)仿真方法，確定最優(yōu)阻尼曲線。

分別將4種非線性阻尼曲線代入圖3所示的車輛-軌道-隧道耦合動(dòng)力學(xué)分析模型中進(jìn)行優(yōu)化計(jì)算，優(yōu)化目標(biāo)為隔振器支反力，其結(jié)果如圖14所示。從圖14(a)、(b)隔振器支反力時(shí)域曲線可以看出，在動(dòng)態(tài)荷載較大的位置P1、P2處施加大阻尼可以極大程度抑制動(dòng)態(tài)荷載峰值。從14(c)、(d)、(e)可以看出，線性大阻尼、先大后小非線性阻尼和漸大阻尼在低頻(≤20 Hz)及中高頻(>20 Hz)有較好的振動(dòng)抑制效果。

(a) 漸小阻尼

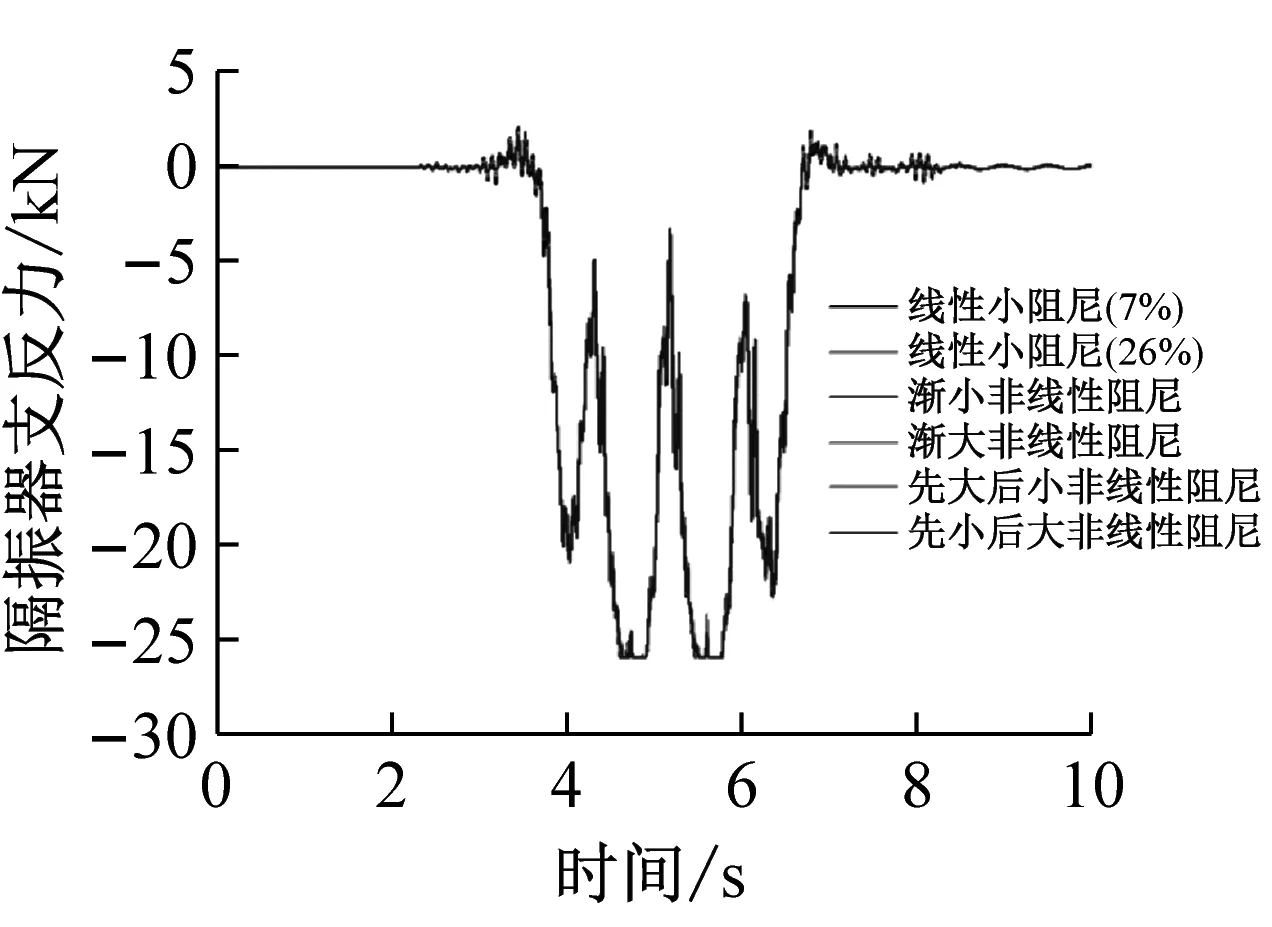
(a) 隔振器支反力

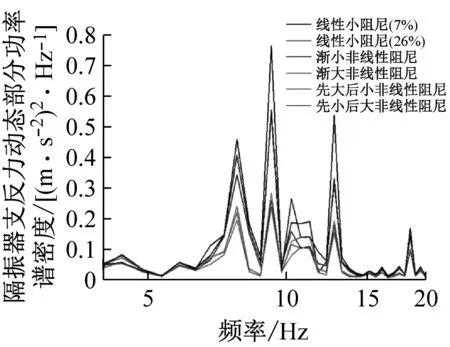
(d) 支反力低頻部分功率譜密度放大圖

6 非線性減振軌道系統(tǒng)仿真驗(yàn)證

將優(yōu)化后得到的非線性剛度和非線性阻尼曲線帶入圖3所示的車輛-軌道-隧道系統(tǒng)動(dòng)力學(xué)模型中，模擬列車運(yùn)行工況下非線性軌道系統(tǒng)的隔振效果和軌道動(dòng)態(tài)響應(yīng)，仿真得到浮置板振動(dòng)加速度及隧道壁分頻振級(jí)圖見圖15(a)、(b)所示。從圖15(a)中可以看出，非線性隔振器可以顯著降低浮置板軌道的振動(dòng)加速度響應(yīng)，振動(dòng)加速度有效值從1.04 m/s2降低到了0.39 m/s2，降低約62%。從圖(b)中可以看出，相比既有線性系統(tǒng)，非線性系統(tǒng)在全頻段都具有較好的衰減效果，Z振級(jí)插入損失約為3 dB；在低頻段(≤20 Hz)，非線性系統(tǒng)的隔振效果遠(yuǎn)優(yōu)于線性系統(tǒng)，分頻最大振級(jí)插入損失約為12 dB。

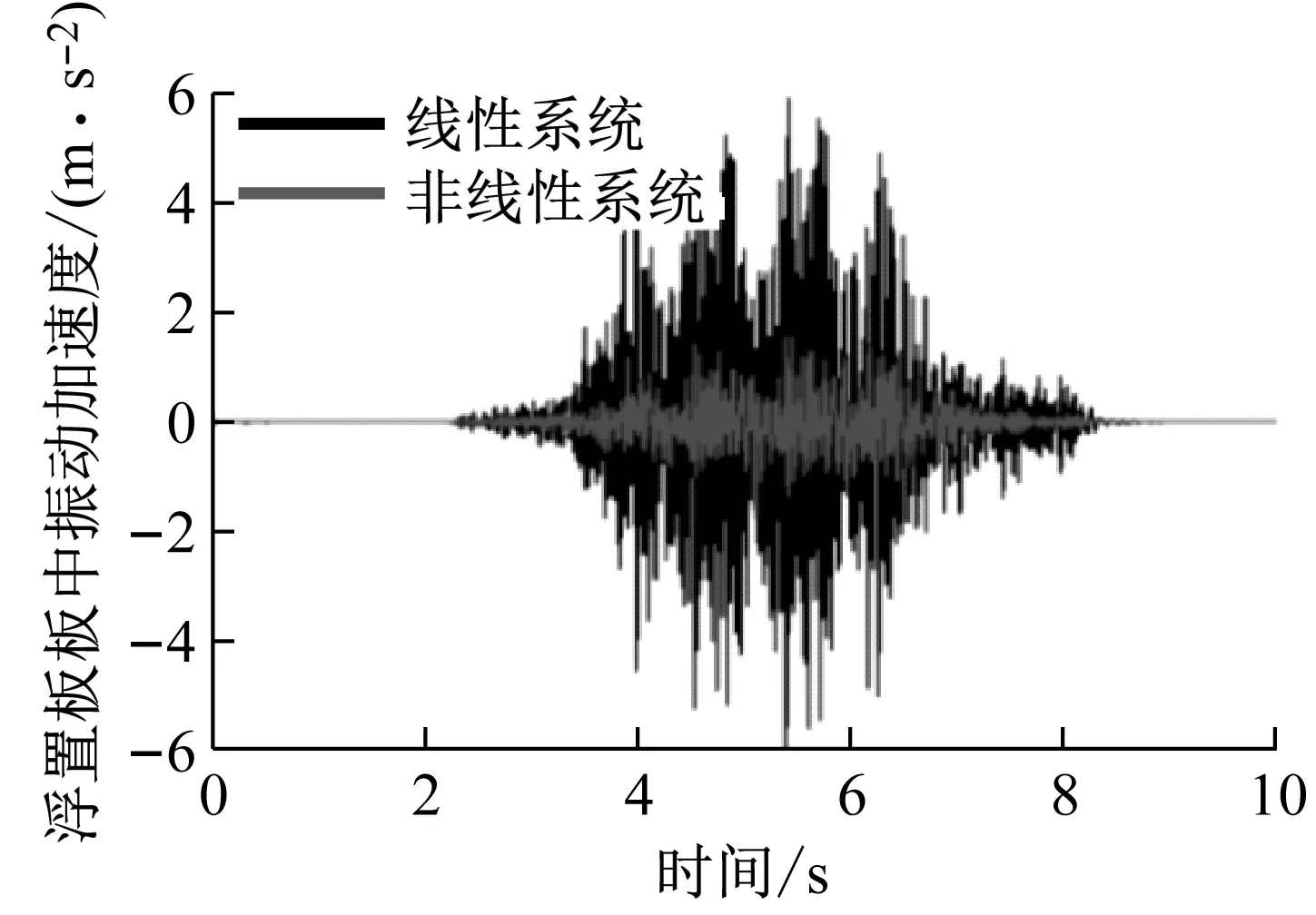
(a) 浮置板加速度

7 結(jié) 論

本文基于非線性隔振理論，在隔振器荷載特征分析的基礎(chǔ)上，對(duì)浮置板減振軌道用隔振器的剛度和阻尼曲線進(jìn)行非線性設(shè)計(jì)優(yōu)化，使得非線性浮置板減振軌道同時(shí)具有良好的低頻隔振性能和動(dòng)態(tài)位移控制能力。利用車輛-軌道-隧道耦合動(dòng)力學(xué)評(píng)估模型進(jìn)行仿真研究，得出以下結(jié)論：

(1) 相比既有線性系統(tǒng)，采用非線性隔振器的非線性浮置板減振軌道系統(tǒng)可有效控制軌道板動(dòng)態(tài)位移，軌道板動(dòng)態(tài)位移可降低約20%。

(2) 相比既有線性系統(tǒng)，非線性浮置板減振軌道系統(tǒng)可顯著降低軌道板的振動(dòng)加速度響應(yīng)，振動(dòng)加速度有效值可降低約62%。

(3) 相比既有線性系統(tǒng)，非線性浮置板減振軌道系統(tǒng)在全頻段都具有較好的衰減效果，Z振級(jí)插入損失約3 dB，在低頻段(≤20 Hz)非線性系統(tǒng)的隔振效果優(yōu)于線性系統(tǒng)，分頻最大振級(jí)插入損失約12 dB。

上述理論研究結(jié)論在實(shí)際應(yīng)用中能否達(dá)到理想效果，應(yīng)在非線性隔振器結(jié)構(gòu)設(shè)計(jì)、制造公差控制和非線性減振軌道系統(tǒng)整體施工上開展系統(tǒng)研究。