頻響函數二次正交法在Davenport風速譜下結構系列響應簡明封閉解的應用研究

葛新廣, 張夢丹， 龔景海， 李創第,

(1.上海交通大學 船舶海洋與建筑工程學院，上海 200240；2.廣西科技大學 土木建筑學院，廣西 柳州 545006)

隨著建筑結構分析能力和建造水平的不斷提高，建筑結構向高、輕、柔方向發展，從而導致高層建筑對風的敏感性十分突出。此外，隨著自然環境的不斷惡化，各類極端天氣的發生都伴隨著破壞性強風出現，因此，建筑結構的抗風研究至關重要。大量的研究表明[1-2]，強風對建筑物的振動作用是由短周期的脈動風所引起的。工程上研究強風對結構的影響有風洞試驗方法[3-4]、CFD模擬[5-6]和隨機風振理論法[7-8]三種方法。其中，風洞試驗方法結果較為準確，但試驗成本較高，常采用縮尺模型試驗獲得風荷載體型系數之后采用理論方法對建筑結構進行風振響應分析。CFD方法是通過數值手段模擬結構物的繞流場并考慮流固耦合作用的一種結構風振響應分析方法，但模擬時對計算機要求較高，且耗時久，分析精度受數學模型的選擇控制。而隨機風振理論法，則是將強風作為結構分析的荷載，利用風的功率譜概念來表述脈動風的動力作用。對于建筑結構而言，該方法基本能滿足工程精度要求，且具有計算分析相對簡單、能與建筑結構恒載、其他活載進行作用效應組合以便于工程設計的特點。Davenport及李創弟等分別提出了隨機風速譜，其中Davenport風速譜應用最為廣泛，成為各國建筑風荷載取值的依據。

隨機風振響應的分析方法主要有頻域法[9-12]和時域法[13]。頻域法中結構響應的功率譜可表示為結構的頻響函數與風激勵功率譜的乘積，表達式簡潔明了。頻域法的典型方法為傳遞函數法和虛擬激勵法。李創第等利用傳遞函數法研究了巴斯金譜激勵下的黏彈性耗能結構的風振響應，但其結構的響應等效為振子的二階振動方程基于巴斯金譜風速譜下的響應，所得結構響應方差的表達式較為復雜。張文首等[14]基于虛擬激勵法研究了基于Davenport風速譜激勵下的結構響應功率譜，研究表明虛擬激勵法所獲得的結構風振響應為CQC(完全平方法)解，但結構響應譜矩(方差)分析時需要數值積分，積分精度和運算效率受積分區間和積分間距影響。趙中偉等[15]利用本特征-虛擬激勵法研究了大跨度鋼結構基于Kaimal譜下的施工過程中的風振響應，研究表明，虛擬激勵法可高效獲得結構風振響應功率譜，但存在需要數值積分響應方差的問題。時域法中，結構響應的協方差表示為結構脈沖函數與激勵協方差的二重積分，而Davenport風速譜無協方差，故時域法在分析風振響應時需要轉為頻域法進行求解。曹宏等利用實模態解耦法給出了經典阻尼結構基于Davenport譜下的風振響應的解析解；鄒萬杰等[16]利用復模態法研究了非經典阻尼結構基于Davenport譜下的風振響應的解析解，推廣了曹宏等的方法的應用范圍。時域法所得結構風振響應的0階、2階及4階譜矩表達式較為復雜，不利于工程應用。

針對上述既有方法的不足，本文首次提出了結構頻響函數二次正交法，并成功獲得了結構基于Davenport風速譜激勵下系列響應(結構層絕對位移及其振動速度、層間位移及其變化率)0-2階譜矩及4階譜矩的簡明封閉解。首先，利用給出考慮豎向空間相關性的脈動風壓功率譜密度函數的簡明表達式；其次，綜合應用復模態法和虛擬激勵法獲得結構風振響應(結構層絕對位移及其振動速度、層間位移及其變化率)的二次正交功率譜密度函數的簡明表達式；最后，根據隨機振動理論中譜矩的定義，獲得了結構風振響應的0階、1階、2階及4階的譜矩的簡明封閉解。

1 風壓力功率譜

脈動風是引起建筑結構振動的關鍵因素，建筑結構在風荷載作用下的脈動風壓力表示為

pf(Hi,t)=I0(Hi)B(Hi)u(t)

(1)

式中：pf(Hi,t)為離地Hi高度處的脈動風壓力值；I0(Hi)是方差為1的隨機變量，其表示脈動風壓的空間相關性；u(t)為風速譜。B(Hi)為風壓力強度系數

(2)

式中：Ai,μs(Hi)、μz(Hi)、w0分別為離地高度為Hi的迎風面積、風荷載體型系數、風壓高度變化系數和基本風壓值；Kr為與地面粗糙度有關的系數。

Davenport風速譜有著廣泛工程應用，其功率譜密度函數

(3)

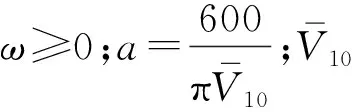
由于任意兩質點所受的脈動風壓力不可能同時達到最大值,須考慮空間位置的相關性，則考慮空間相關性的平穩脈動風壓pf(Hi,t)和pf(Hj,t)的協方差

CPf(Hi,Hj,τ)=E[pf(Hi,t)pf(Hj,t+τ)]=

B(Hi)B(Hj)E[I0(Hi)I0(Hj)]Cu(τ)

(4)

式中：

(5)

令：

(6)

則考慮空間相關性后的風壓協方差為

CPf(Hi,Hj,τ)=ρijCu(τ)

(7)

由Wiener-Khinchin定律，考慮空間相關性的風壓功率譜為：

(8)

把式(7)代入式(8)，考慮空間相關性的風壓功率譜與Davenport風速譜存在簡明關系

SPf(Hi,Hj,ω)=ρijSu(ω)

(9)

2 結構系列響應的頻響函數的二次正交法

建筑結構在脈動風荷載Pf作用下的運動方程為

(10)

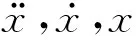
風對結構的作用常取前m振型，設

x=φmq

(11)

式中：φm為結構前m振型，其為m×n矩陣;q為第廣義坐標向量，q=[q1…qm]T，“T”為向量的轉置。

把式(11)代入式(10)并由式(10)與實模態的正交性，結構的振動方程改寫為

(12)

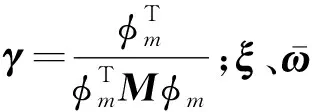
引入狀態變量

(13)

則式(10)改寫為

(14)

其中：O2為m×m矩陣，其元素均為0；E1為m×m的單位對角矩陣。

根據復模態法理論，式(14)存在左、右特征向量V、U和特征值矩陣P使之解耦，即存在如下關系

(15)

式中，特征值矩陣P為對角陣，其元素的實部為負實數。

引入復模態變換

y=Uz

(16)

由復模態理論，式(14)改寫為

(17)

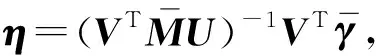
由于P為對角陣，式(17)的分量形式

(18)

式中：ηk表示η矩陣第k行的元素。

根據虛擬激勵法，并由式(9)風壓譜與風速譜的關系，則式(18)的頻域解

(19)

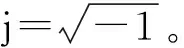
由式(11)、(13)和(16)，則結構響應的頻域解

(20a)

(20b)

(20c)

(20d)

從式(20)可知，結構響應的位移及速度可統一表示為

(21)

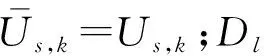
由虛擬激勵法，則Dl的功率譜為

(22)

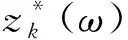
針對式(22)可獲得其更為簡潔的表達式

SDl(ω)=HDl(ω)Su(ω)

(23)

式中,HDl(ω)為結構的頻域響應函數，其的正交化形式為

(24)

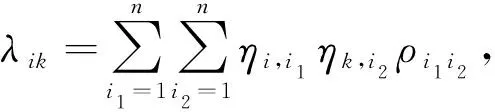
式(24)的具體推導過程見附錄A。

由式(23)可知，結構基于Davenport風速譜系列響應功率譜等于結構的頻響函數與風速譜的簡單乘積。由式(24)可知，結構響應的頻響函數可表示為結構振動復特征值pi(i=1～2m)與頻域變量ω平方和的線性組合，具有正交性的特征，故稱之為頻響函數的二次正交化。所獲得頻響函數為顯示解，且具有簡潔性，為后文獲得結構響應譜矩和方差的簡明封閉解奠定基礎。

3 結構風振響應譜矩的簡明封閉解法

根據隨機振動理論，隨機激勵下線性結構位移/層間位移的0階譜矩等于位移/層間位移的方差。位移/層間位移的2階譜矩等于速度/層間位移變化率的0階譜矩，等于速度/層間位移變化率的方差。位移的4階譜矩等于速度的2階譜矩，等于加速度的0階譜矩，即速度的2階譜矩等于加速度的方差。結構振動加速度是建筑舒適度[17-18]分析的基礎；位移/層間位移響應的1階譜矩是動力可靠度[19]譜參數分析的重要參數之一。為此需要對結構風振響應的0-2階譜矩和4階譜矩進行分析。

根據隨機振動原理，結構響應的譜矩定義

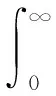
(25)

3.1 結構響應0-2階譜矩的簡明封閉解

把式(23)代入式(25)

統計學處理 采用SPSS 23.0、Stata 14.0統計軟件對數據進行處理。通過SPSS 23.0對數據進行描述分析，將數值變量轉化為分類變量，通過單因素方差分析和卡方檢驗，比較不同年份研究對象年齡、性別及發病率的差異性。采用單因素分析和卡方檢驗分析研究對象在開放式隊列中哮喘發病的影響因素。由于本研究發生哮喘結局的研究對象人數所占總的觀察對象比例較小，因此，多因素分析采用適用于罕見結局發生率的多因素Poisson回歸模型，使用Stata 14.0統計學軟件建立多因素Poisson回歸模型，將哮喘發生結局作為被解釋變量納入Poisson回歸模型中，該模型設定P<0.05具有統計學意義。

(26)

式中：Χk,q的計算見附錄B

(27)

對式(27)當q=0，2時進行積分得

(28a)

(28b)

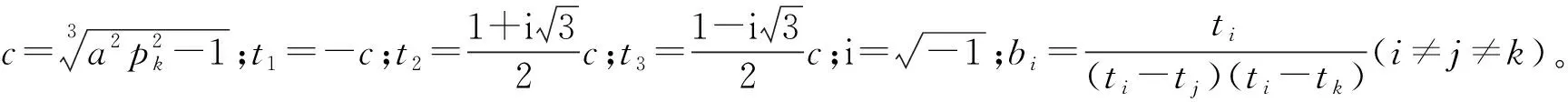
對式(26)，當q=1時進行積分，得：

(29)

3.2 風振加速度方差的簡明封閉解

由隨機振動理論，風振加速度方差等于風振絕對位移變化率的2階譜矩，故由式(28b)可獲得結構振動的加速度的方差

(30)

4 算 例

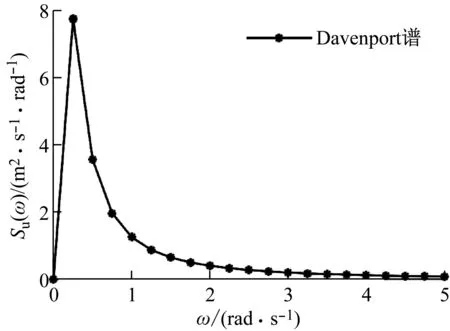
圖1 Davenport風速功率譜Fig.1 Speed PDF of Davenport

4.1 本文方法驗證

4.1.1 結構系列響應功率譜對比分析

為驗證本文方法中結構頻響函數二次正交化的正確性，就結構系列響應的功率譜密度函數利用本文方法與傳統虛擬激勵法進行對比分析，如圖2和3所示。從圖中可知，本文方法與傳統虛擬激勵法的結構響應功率譜密度函數完全吻合，從而說明結構頻響函數二次正交化法的正確性。由于傳統方法的功率譜表達式為式(22)，而本文方法的功率譜表達式為式(23)，故本文方法的功率譜更為簡潔。

4.1.2 系列響應譜矩的對比分析

為驗證本文所獲得的結構風振系列響應0-2階譜矩及加速度方差的正確性，與虛擬激勵法進行對比分析。由于虛擬激勵法分析結構響應譜矩和方差時受積分步長和積分區間的影響較大，積分區間上限暫定1 000 rad/s,積分步長取3種，具體如圖4～8所示。由圖可知，隨著積分步長的減少，虛擬激勵法所得譜矩與本文方法越來越接近，說明本文方法的正確性。同時說明，虛擬激勵法在分析隨機響應譜矩時積分步長的選擇對于響應精度非常重要。

圖2 第1層位移功率譜對比圖

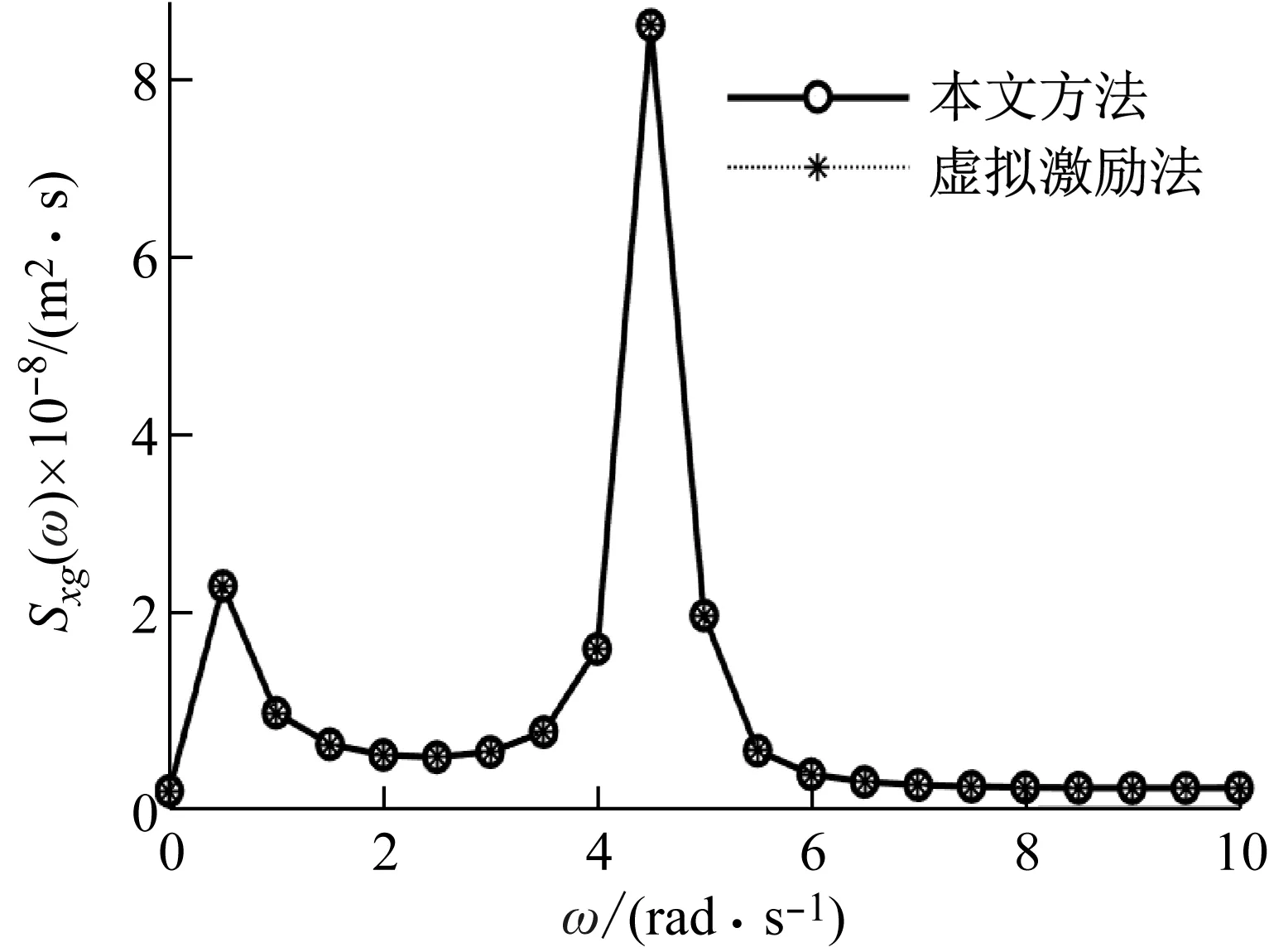
圖3 第10層層間位移功率譜對比圖Fig.3 Comparison of PDF of interlayer displacement of10th floor

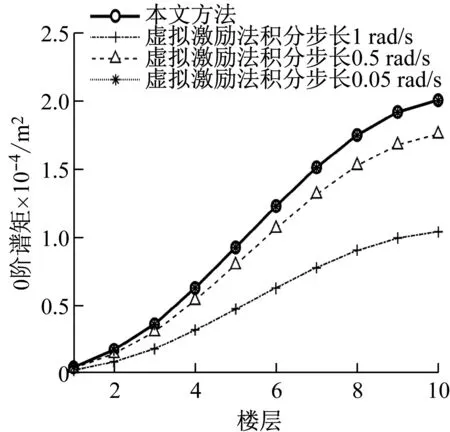
圖4 位移0階譜矩對比圖Fig.4 Comparison diagram of 0 orderspectral moment of displacement

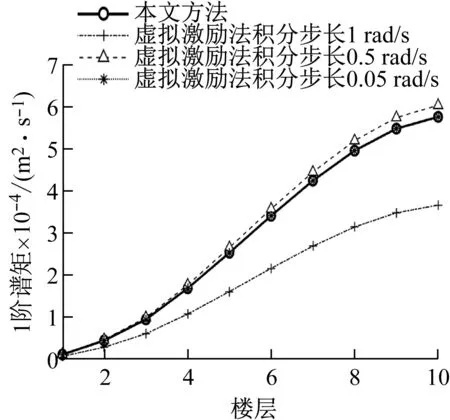
圖5 位移1階譜矩對比圖Fig.5 Comparison diagram of 1st orderspectral moment of displacement

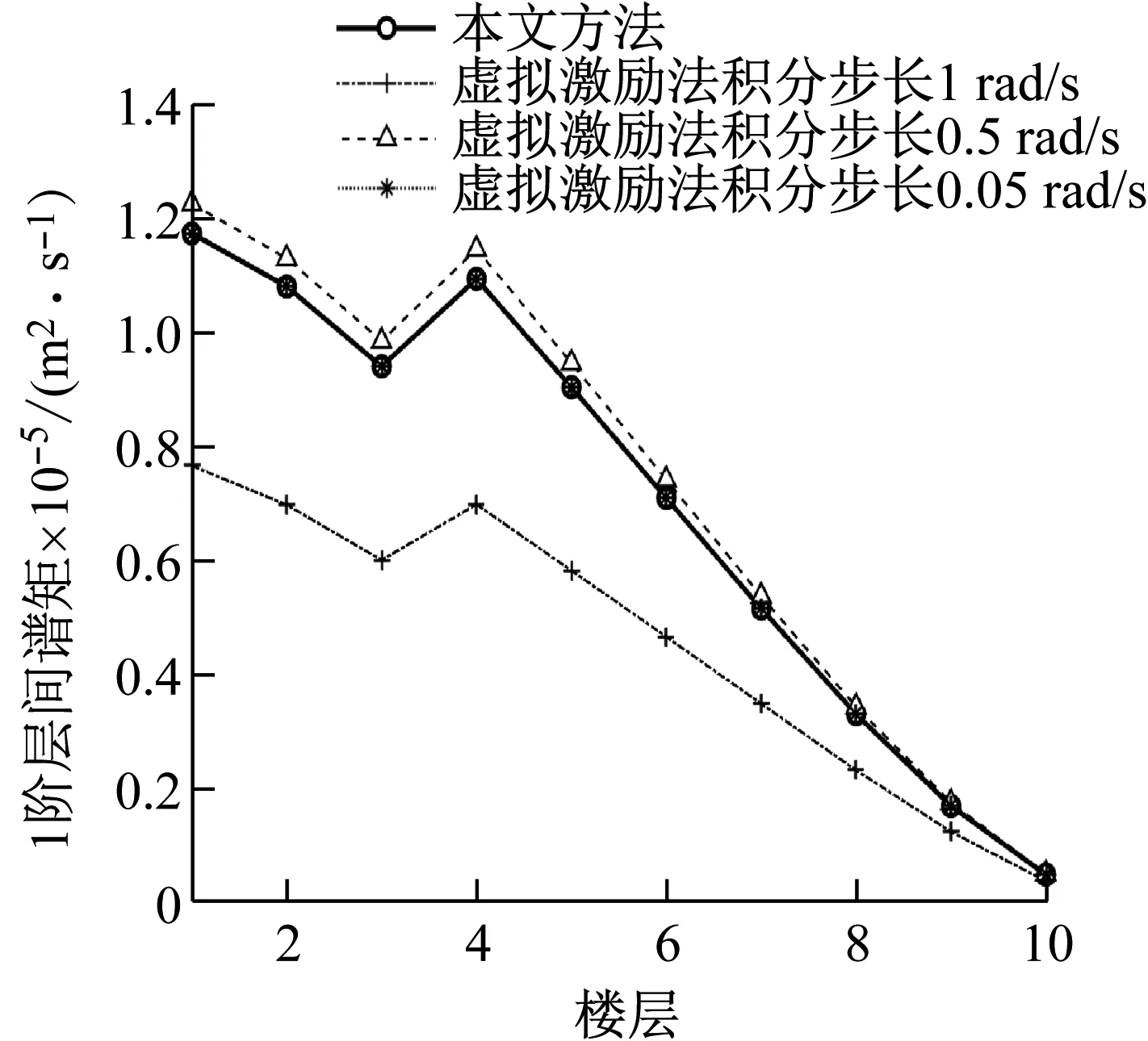
圖7 層間位移1階譜矩對比圖Fig.7 Comparison diagram of 1st order spectralmoments of interlayer displacement

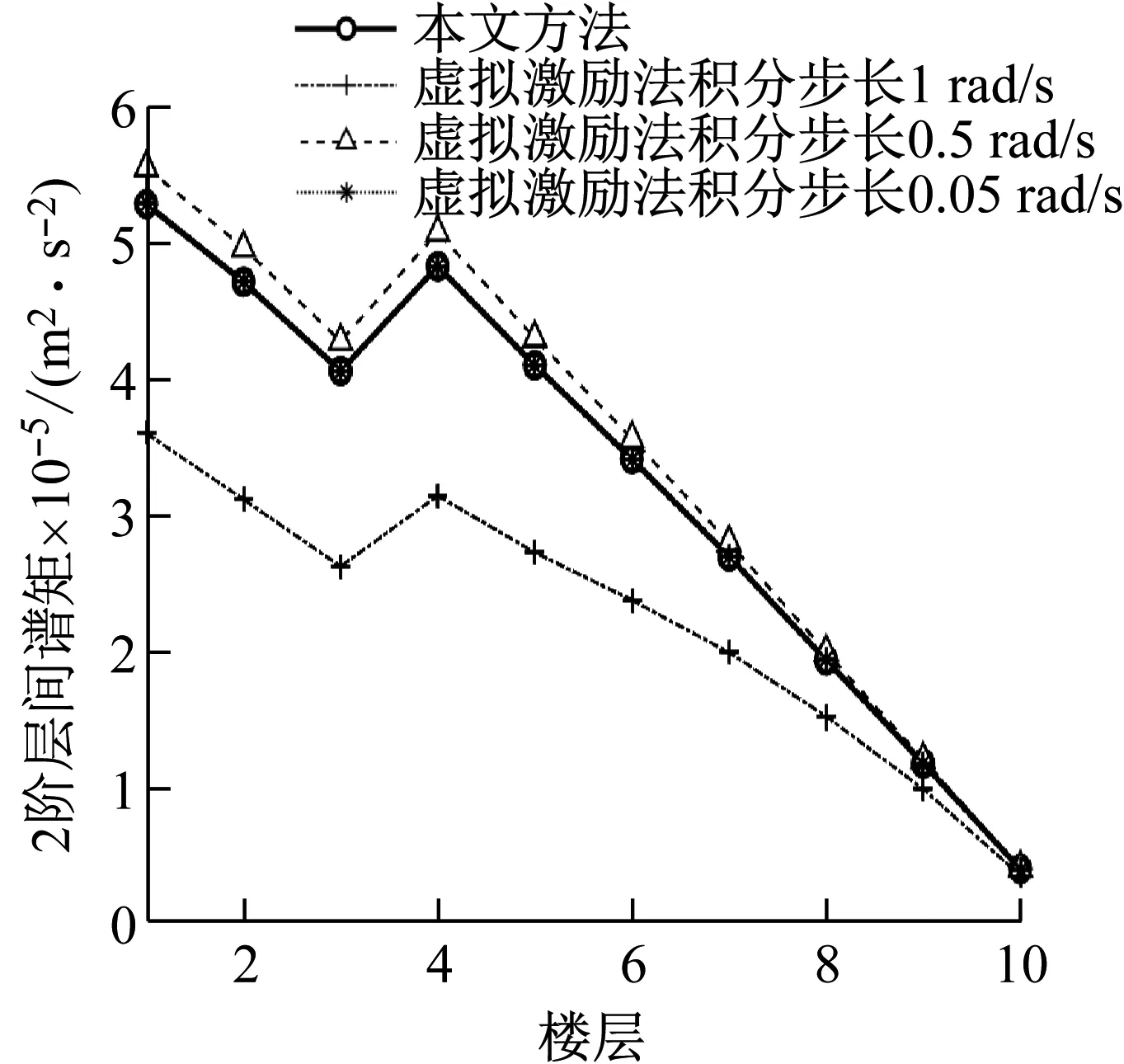
圖8 層間位移2階譜矩對比圖Fig.8 Comparison diagram of 2nd order spectralmoments of interlayer displacement

4.2 虛擬激勵法積分區間的確定

由“4.1節”可知，本文方法所獲得譜矩為精確解，且可用來驗證虛擬激勵法的精度。而目前文獻對于虛擬激勵法的積分區間沒有明確的規定，為此，本文對其合理的積分區間進行了研究?！?.1節”研究表明積分步長取0.05時虛擬激勵法基本與本文方法重合，為此，分別取積分區間上限為5 rad/s，25 rad/s，100 rad/s，按積分步長為0.05 rad/s進行分析。從圖9～12可知，積分上限取25 rad/s,結構響應0-2階譜矩和加速度方差均可以達到較好的精度。

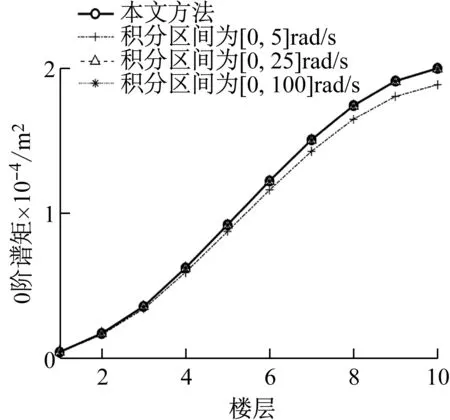
圖9 虛擬激勵法中積分區間對位移0階譜矩影響Fig.9 Influence of integral interval on 0 order spectralmoment of displacement by PEM

圖10 虛擬激勵法中積分區間對位移1階譜矩影響Fig.10 Influence of integral interval on 1 st order spectralmoment of displacement by PEM

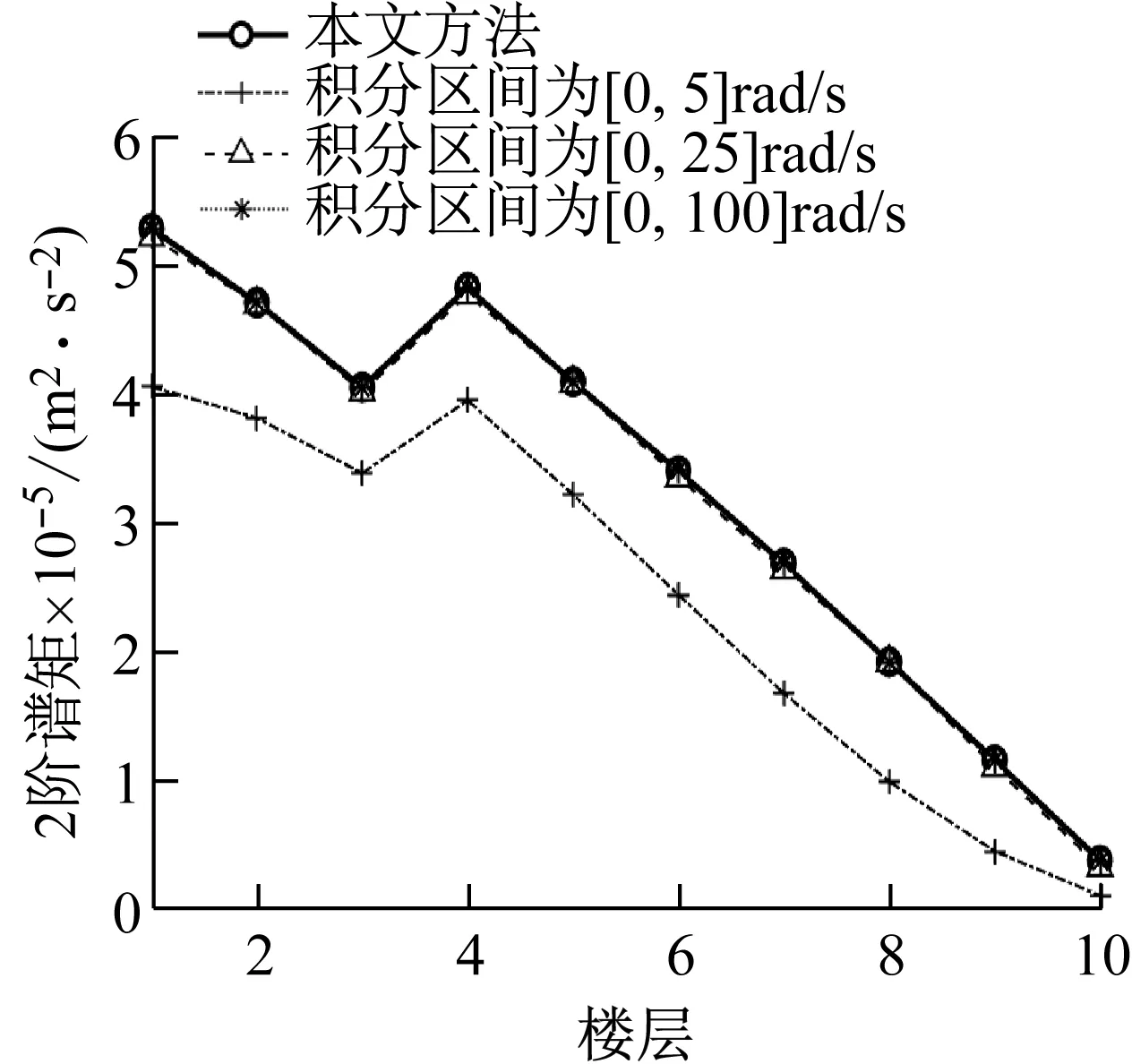
圖11 虛擬激勵法中積分區間對層間位移2階譜矩影響Fig.11 Influence of integral interval on 2nd order spectralmoment of interlayer displacement by PEM

5 結 論

本文提出了結構頻響函數的二次正交法，并成功獲得了結構基于Davenport風速譜激勵下系列響應的0-2階譜矩及4階譜矩的簡明封閉解，獲得如下結論：

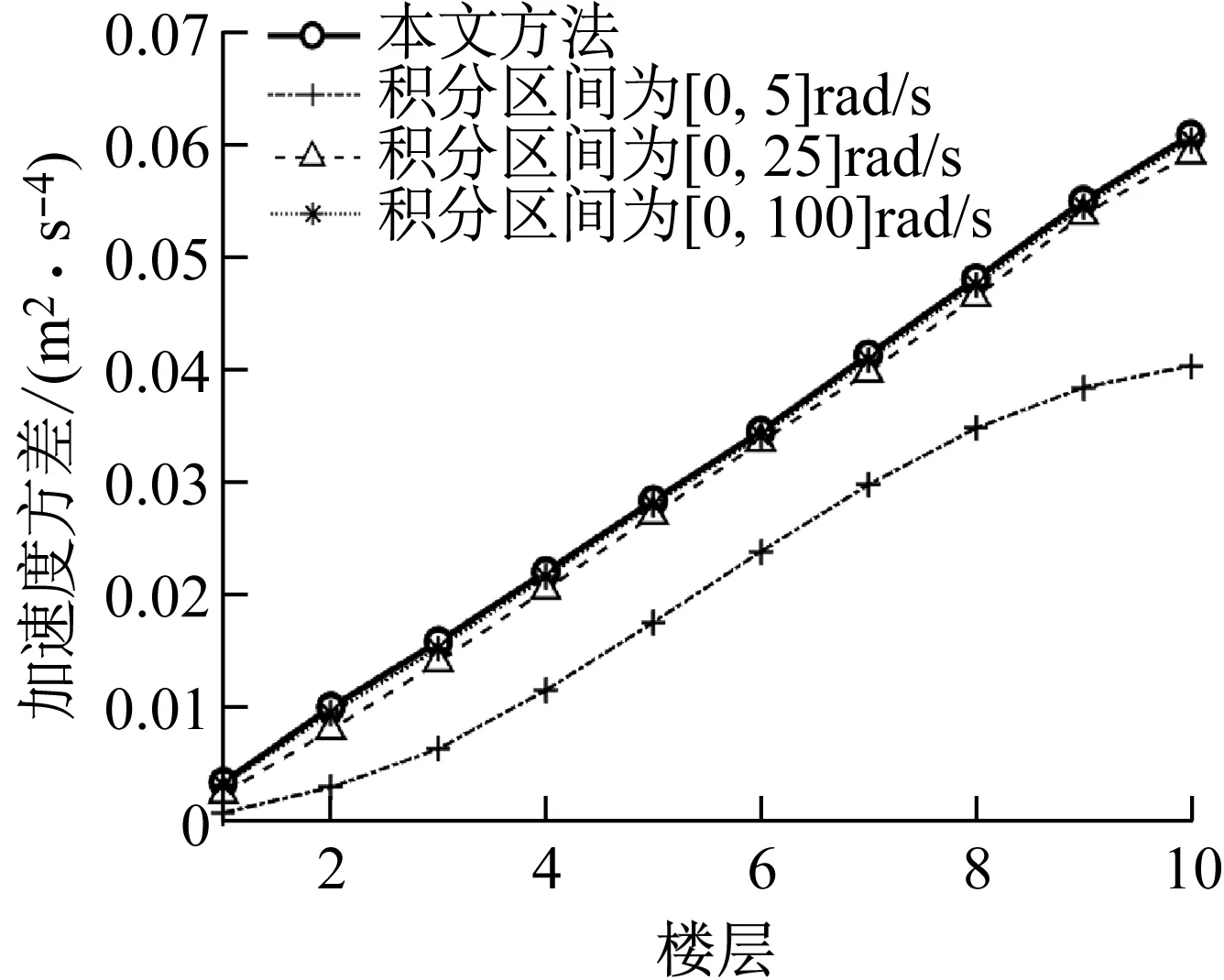
圖12 虛擬激勵法中積分區間對結構加速度方差影響Fig.12 Influence of integral interval on structuralacceleration variance by PEM

(1) 應用復模態法將結構振動體系解耦為一階微分方程組，利用一階微分方程的虛擬激勵法獲得了結構系列風振響應(結構層絕對位移和層間位移)的功率譜密度函數，該函數是關于系統振動復特征值與頻域變量的平方和的線性組合，稱之為頻響函數的二次正交化。

(2) 由于獲得了結構系列響應功率譜的二次正交式，從而利用譜矩的定義成功獲得了結構風振響應的0-2階及4階的譜矩的簡明封閉解。而響應的0階譜矩等于響應的方差，2階譜矩等于響應變化率的方差，從而獲得了結構系列響應的方差，為基于首超破壞的動力可靠度分析奠定了基礎。

(3) 通過與傳統虛擬激勵法進行對比，說明本文方法分析結構系列響應的譜矩和方差為封閉解，不受積分區間和積分步長的影響；同時可以用來驗證傳統虛擬激勵法的精度。

附錄A 頻響函數SDl(ω)的推導

對文中式(22)進行整理：

(A.1)

式中：

(A.2)

(A.3)

(A.4)

把式(19)代入式(A.3)：

利用式(9)，則式(A.5)簡化為：

(A.6)

(A.7)

把式(19)代入式(A.4)：

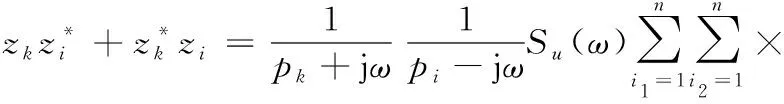
ηi,i1ηk,i2I0(Hi1)I0(Hi2)B(Hi1)B(Hi2)+

I0(Hi1)I0(Hi2)B(Hi1)B(Hi2)

(A.8)

由式(9)，則式(A.8)改寫為：

(A.9)

(A.10)

針對式(A.9)中的以下部分進行簡化：

把式(A.11)代入式(A.9)則：

(A.12)

把式(A.6)、(A.12)代入式(A.1)，則結構脈動風壓力的動力響應的功率譜：

(A.13)

附錄BΧk,q(q=0,2)的推導

B.1Χk,0的推導

(B.1)

令：

t=(1+a2ω2)1/3

(B.2)

由式(B.2)得：

(B.3)

把(B.2)、(B.3)代入式(B.1)：

(B.4)

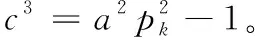
對式(B.4)中部分進行因式分解：

(B.5)

對式(B.5)進一步簡化：

(B.6)

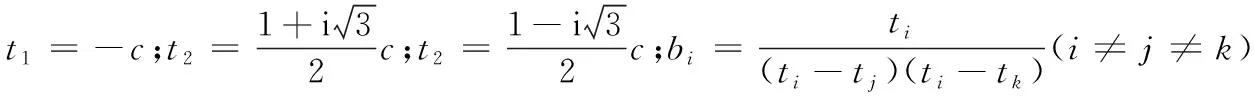
把式(B.6)代入式(B.4)并積分：

(B.7)

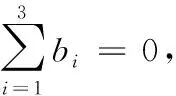
(B.8)

B.2Χk,2的推導

令：t=(1+a2ω2)1/3，則

(B.10)

(B.11)

把式(B.11)代入式(B.9):

(B.12)