基于Tech Demo Sat-1衛星的GPS反射信號海面高度反演

張云，馬德皓，孟婉婷，鄭俏，楊樹瑚，*

(1.上海海洋大學 信息學院，上海 201306；2.上海航天電子技術研究所，上海 201109）

海面高度(Sea Surface Height，SSH）是海洋科學研究中的重要一環［1］。GNSS反射信號(GNSSR）是當前海面高度測量中發展較快的遙感技術，該技術在1993年由Martin-Neira［2］首次提出，并迅速成為國內外的研究熱點。GNSS-R技術通過接收到的左右旋反射信號之間的差異或反射信號與直射信號之間的差異進行反射面物理量的反演，相對于傳統的遙感技術有多方面的優點，如可實現低成本實時監測、擁有大量信號源、不受天氣影響［3-4］。

相對于岸基GNSS-R［5-6］與機載GNSS-R海面高度反演，星載GNSS-R海面高度反演技術的探測范圍更廣，可以實現全球范圍監測。目前，世界上已經發射了多顆星載GNSS-R接收衛星，如DMC(Disaster Monitoring Consortium）聯盟的UK-DMC和UK-DMC2衛星、英國薩里衛星技術有限公司的TDS-1(Tech Demo Sat-1）衛星、美國國家航空航天局(NASA）的旋風全球導航衛星系統(CYGNSS）。2019年6月5日，中國自主研發自研的GNSS-R接收衛星——捕風一號A／B衛星發射成功，國內對星載GNSS-R的研究利用開始了新時代。

目前，利用星載GNSS-R技術進行海洋監測方面的研究主要集中在海面測風等領域，海面高度反演領域的研究較少。2015年，劉風玲等［7］使用UK-DMC數據對星載GNSS-R海洋探測可行性進行了分析；2016年，Clarizia等［8］使用TDS-1數據，對星載GNSS-R海面高度反演進行了初步研究，以DTU10(Danmarks Tekniske Universitet 10）平均海平面模型為驗證模型，分別在北太平洋和南大西洋進行了驗證；2018年，Mashburn等［9］使用TDS-1數據，對星載GNSS-R海面高度反演進行分析，使用DTU10平均海平面模型與電離層模型、對流層模型等建立HiFi模型作為驗證模型，在全球范圍內對高度反演結果進行了驗證；2019年，李偉強等［10］通過使用CYGNSS數據，分別采用重跟蹤峰值功率的百分比點(HALF）、重跟蹤波形一階導數最大的點(DER）、重跟蹤實測波形與仿真波形擬合誤差最小點(FIT）等方法，對星載GNSS-R海面高度反演進行了分析；同年，萬瑋等［11］使用TDS-1數據，對全球湖泊水位進行反演，并與采用CryoSat-2衛星、Jason衛星、Envisat衛星數據反演的結果進行對比，發現TDS-1衛星對湖面的反演結果與其他反演數據有良好的一致性，但存在較大誤差。這些研究主要集中討論了星載GNSS-R海面和湖面高度反演的可行性，對于星載海面高度反演模型中的誤差分析較少。

本文致力于研究高精度星載GNSS-R海面高度測量。由于TDS-1衛星公開數據中僅提供了GPS反射信號(GPS-R）數據，本文通過使用TDS-1數據，在機載GPS-R海面高度反演模型的基礎上［12］，著重分析了星載GPS-R海面高度反演中出現的各類誤差，并建立相應的誤差模型，將誤差模型應用于星載GPS-R海面高度反演模型中，同時采用DTU15(Danmarks Tekniske Universitet 15）全球平均海面模型與DTU全球海潮模型建立DTU驗證模型，驗證星載GPS-R海面高度反演模型的精度。本文對連續20 d的數據進行分析，將反演結果與DTU驗證模型對比，驗證了本文使用的星載GPS-R海面高度反演的誤差模型能夠有效提高反演模型的精度。

1 TDS-1數據

本文使用的數據是由TDS-1衛星采集的GPS-R數據中的L1B數據，來源于MERRByS網站(www.merrbys.co.uk）。

TDS-1衛星是由英國薩里衛星技術有限公司于2014年7月8日成功發射入軌的一顆用于提供在軌技術驗證服務的衛星，該衛星在高度為635 km 的太陽同步軌道上。TDS-1衛星上的GPS-R接收機執行實時導航，搭載包括SGR-ReSI在內的8個試驗載荷，通過地面站控制各個載荷以8 d為一個工作周期輪流工作。2018年之前，SGR-ReSI在每個工作周期內工作1～2 d，在2018年2月至12月期間，SGR-ReSI更改為全天模式運行。SGR-ReSI可同時跟蹤、記錄和處理4路GPS L1、L2C及其他導航衛星的地表反射信號，并產生1 s非相干累加的時延多普勒圖(Delay-Doppler Map，DDM）數據［13］。表1為TDS-1衛星的參數。

表1 TDS-1衛星參數Table 1 Param eters of satellite TDS-1

TDS-1衛星提供的L1B數據格式為NetCDF格式。在TDS-1衛星的全天候采集下，每天的數據以6 h為間隔被分為H00、H06、H12和H18四組存放，每組數據中均提供了DDM、Metadata等文件。

本文使用了TDS-1衛星提供的2018年4月10日至2018年4月30日連續20 d的L1B數據中的DDMs.nc與Metadata.nc文件。其中，DDMs.nc文件中保存了所采集到的DDM 數據，Metadata.nc文件存放了與DDM 數據對應的各項參數。本文使用了TDS-1衛星的軌道參數、信號采集時間和地點、接收天線溫度等數據。

2 星載GPS-R海面高度反演

2.1 星載GPS-R海面高度反演的幾何原理

本文海面高度測量的幾何原理如圖1所示，參考橢球采用WGS84橢球體。

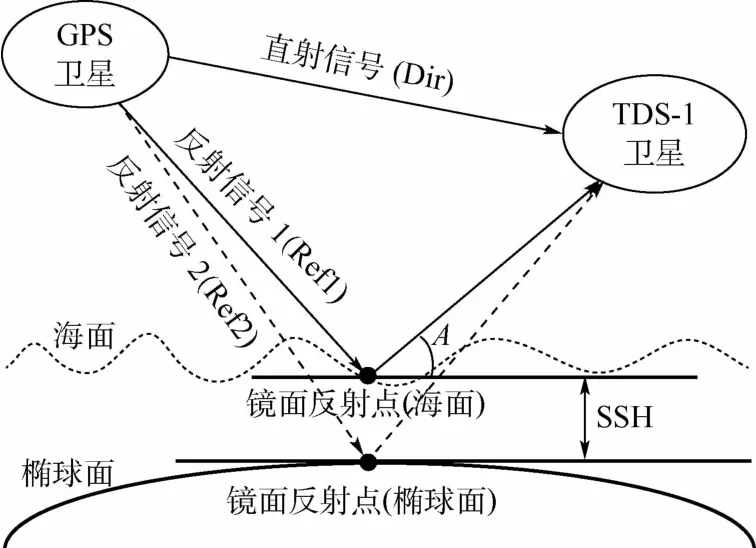
圖1 星載GPS-R海面高度反演幾何原理Fig.1 Geometric principles of satellite-borne GPS-R sea surface height inversion

GPS衛星與TDS-1衛星之間的直射延遲為Dir，在海面上的反射信號延遲為Ref1，在橢球面上的反射信號延遲為Ref2［14］，可得

式中：Delay為GPS衛星與TDS-1衛星在海面與橢球面的延遲距離差；c為光速。

繼而可得出初步反演的海面高度為

式中：A為反射仰角。

式(2）成立需要有以下假設：

1）GPS衛星與接收機衛星距離海面足夠遠，因此海面與橢球面間的反射仰角差異可忽略不計。

2）海面的反射點為平面［9］。

基于以上假設，利用圖1幾何關系與式(1）、式(2），可進行GPS-R海面高度測量。

2.2 星載GPS-R海面高度反演的誤差分析

2.2.1 星載GPS-R海面高度反演的誤差

星載GPS-R信號在傳播過程中，會出現各種導致信號傳播誤差的因素。這些因素若不進行分析與修正，則會導致星載GPS-R海面高度反演的精度下降，因此需要進行誤差分析以提高反演精度。

導致誤差出現的因素主要有電離層、對流層、天基線姿態誤差、GPS衛星軌道誤差、TDS-1衛星軌道誤差和反射信號延遲誤差等。圖2為影響GPS-R信號的主要誤差示意。

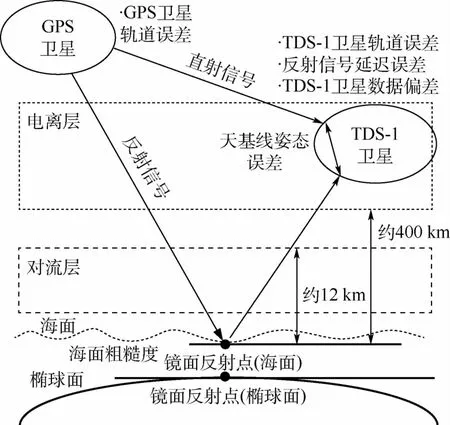
圖2 影響GPS-R信號的主要誤差Fig.2 Main errors affecting GPS-R signal

2.2.2 星載GPS-R海面高度反演的誤差解析

1）電離層延遲距離誤差與對流層延遲距離誤差

本文對電離層延遲距離誤差(Delayion）的補正使用的是國際參考電離層模型(IRI2016）［15］；對流層延遲距離誤差(Delaytro）進行補正［16］：

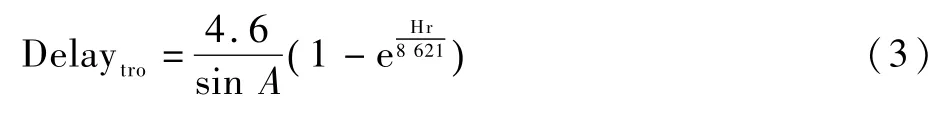
式中：Hr為TDS-1衛星在垂直方向與鏡面反射點的高度差。

2）軌道誤差與天基線姿態誤差

在GPS衛星軌道數據的使用中，本文參考了IGS(International GNSS Service）提供的SP3精密星歷數據，用以精確定位GPS軌道［17］；并通過TDS-1衛星提供的軌道數據，校正了TDS-1衛星軌道誤差(Delaytds-track）和天基線姿態誤差(DelayAntenna）。

3）反射信號延遲誤差

構造圖1所示的反射信號幾何模型，模擬了靜態反射狀態，在實際反射過程中，GPS衛星和TDS-1衛星的運動會造成反射信號延遲。在岸基測高中，由于接收機是固定位置及反射延遲距離差(Delay）較短，會忽略該延遲；而TDS-1衛星運動及衛星位置離鏡面反射點的距離較遠(約800 km），需要建立相關的位置模型消除該誤差。

由于確定信號發出的時間比確定信號接收的時間要復雜，且在信號傳輸過程中信號路徑會發生偏移，本文在研究中使用圖3(a）所示的幾何模型［18］。

圖3(a）中的幾何模型假定直射信號與反射信號同時發出，接收機在T1時刻接收到直射信號，且在T2時刻接收到反射信號。因此，實際反射信號與直射信號的延遲距離差Delaycorr為

圖3 考慮接收機和發射機運動的幾何模型Fig.3 Geometric model considering receive rmotion and transmitter motion

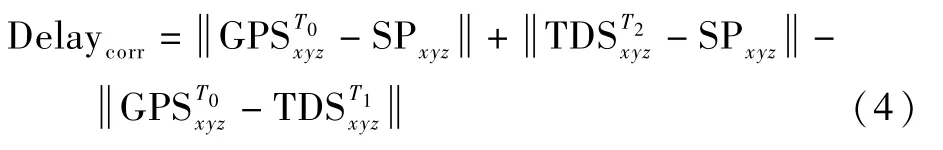
而未加修正的反射信號與直射信號的延遲距離差Delayorignal為

由于TDS-1衛星提供的L1B數據僅有對應每個索引當前時間的變量，本文依據數據與圖3(a），作出以下假設：

①數據中提供的GPS位置為直射信號與反射信號發出時的位置。

②數據中提供的TDS-1位置為TDS-1衛星接收到直射信號時的位置，即

③鏡面反射點位置不變。

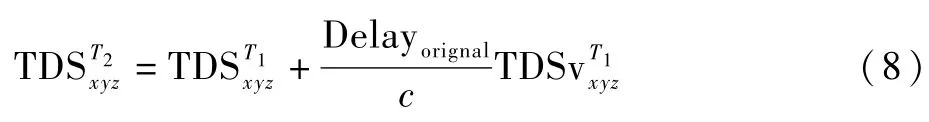
綜上，可得反射信號延遲誤差DelayRDError為

經過TDS-1數據分析，計算出DelayRDError約為±10 m。

4）趨勢誤差

TDS-1衛星每間隔1 s采樣一個鏡面反射點樣本，但由于TDS-1衛星接收機中接收直射信號的直射通道與接收反射信號的反射通道在接收信號時存在延遲，造成了約為±0.1 s的信號接收偏差，該偏差導致DDM 中開環跟蹤點定位不準確，造成了在高度反演中約為±50 m 的趨勢誤差(DelayTrend）［9］。

由于隨機偏差的存在，本文通過使用驗證模型對測量高度進行輔助修正。

2.2.3 星載GPS-R海面高度反演的誤差修正

通過對誤差的分析，對式(1）中計算的初步反演的延遲距離差(Delay）進行誤差修正，得到精確的海面高度反演結果為

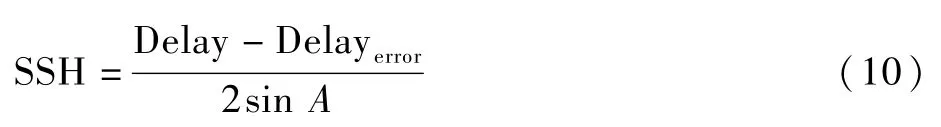
式中：Delayerror為上述所有誤差因素所造成的延遲距離誤差，即

表2為Delay的各項誤差及其補正方法。

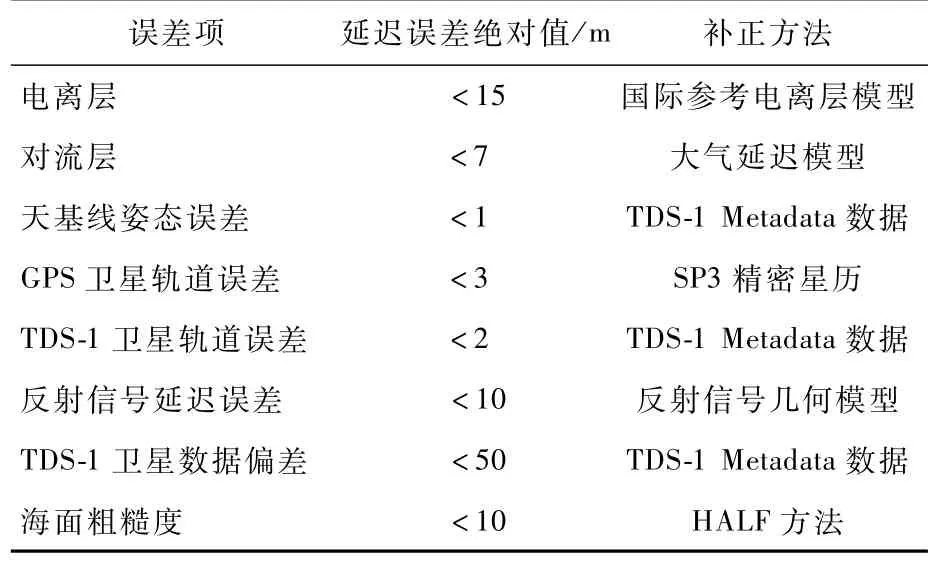
表2 誤差因素及補正方法Table 2 Error factors and correction methods

2.3 驗證模型的建立

在進行星載GPS-R海面高度反演時，需要與實測海面數據進行對比驗證，確定星載海面高度反演的精度。由于缺乏實測數據，應用驗證模型來驗證海面高度反演精度。本文使用由丹麥技術大學開發的DTU15全球平均海面模型(DTU Mean Sea Surface 15，DTUMSS15）與DTU全球海潮模型(DTUTide）組成的DTU 模型作為驗證模型［19］。由驗證模型得到的海面高度SSHmodel為

3 海面高度的反演結果與分析

3.1 星載GPS-R海面高度反演方法

3.1.1 數據篩選

本文使用TDS-1數據來進行分析和處理，并篩選可用數據。使用表3相關閾值對數據進行篩選，且為了消除極地海冰影響，僅保留緯度±70°以內的數據，并去除鏡面反射點位于陸地上的觀測數據和觀測波形出現明顯異常的數據［9］。

表3 篩選參數及范圍Table 3 Filter param eters and scope

3.1.2 數據處理

圖4為TDS-1數據的處理流程。首先，提取TDS-1數據并進行數據篩選；然后，對篩選后的數據進行兩方面處理。

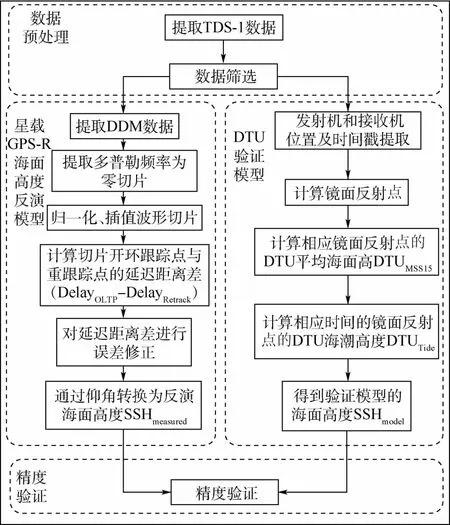
圖4 TDS-1數據處理流程Fig.4 TDS-1 data processing flow

一方面，對DDM 數據進行相關計算。使用TDS-1數據中的DDM 數據(見圖5），提取DDM中多普勒頻率為零的波形切片，并對該波形切片進行歸一化與插值。

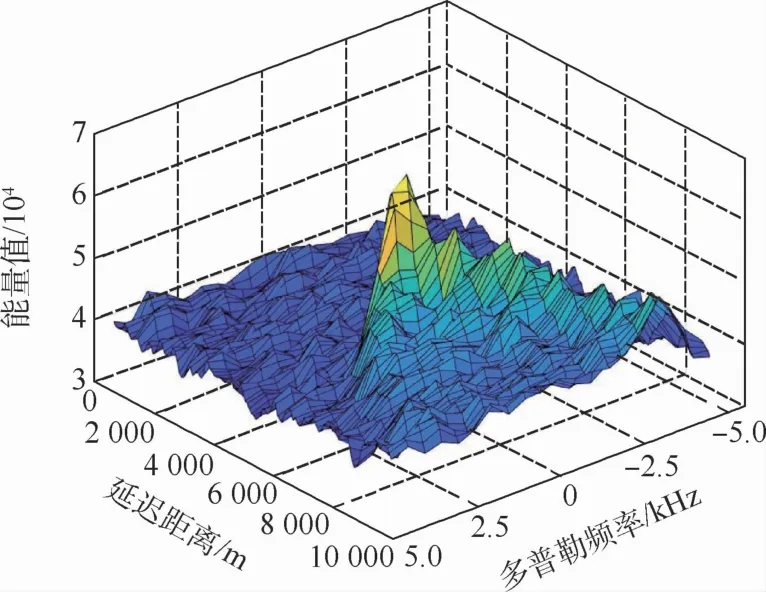
圖5 DDM示例Fig.5 An example of DDM

DDM的波形取決于反射面粗糙度和介電常數。反射面粗糙度決定了散射面積，從而決定了波形的延遲：通過重跟蹤DDM 中相關函數的延遲，即取DDM 多普勒頻率為零切片中重跟蹤點所對應的延遲距離，可以確定海面鏡面反射點的反射信號相對于直射信號的波形窗口內延遲距離(DelayRetrack）；而DDM的延遲維中心點(開環跟蹤點）則為理想狀態下橢球面鏡面反射點的跟蹤點，可以確定橢球面鏡面反射點的反射信號相對于直射信號的波形窗口內延遲距離(DelayOLTP）［9］。本文采用標準單基地雷達技術的HALF方法［20］，計算歸一化波形峰值前沿70%能量值處點為重跟蹤點，同時計算波形延遲維的中心點為開環跟蹤點。圖6為歸一化能量值插值后的波形切片示例，以及重跟蹤點與開環跟蹤點。重跟蹤點與開環跟蹤點的橫坐標分別對應了DelayRetrack與DelayOLTP的取值。

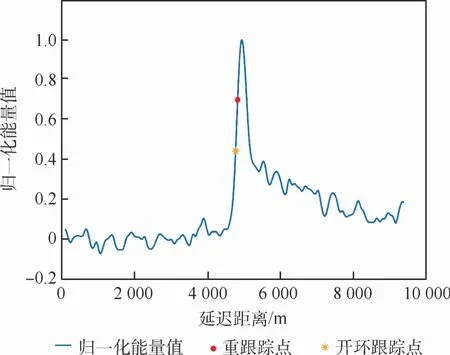
圖6 歸一化能量值插值后多普勒頻率為零的切片Fig.6 Slice with zero Doppler frequency after normalized energy interpolation

在構造圖1所示的反射信號幾何模型中，星載測高模型中的反射延遲距離差(Delay）一定小于波形跟蹤窗口的延遲維距離(約為9 396 m），Ref1對應的跟蹤點一定和Ref2對應的開環跟蹤點落在同一個波形跟蹤窗口內，因此計算DelayOLTP與DelayRetrack的差，可得到橢球面鏡面反射點與海面鏡面反射點的反射延遲距離差(Delay）。式(1）在DDM高度反演中可變形為

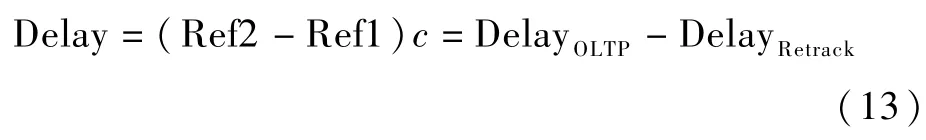
對式(13）進行誤差修正，并結合式(2）和式(10），可反演得到海面高度SSHmeasured為

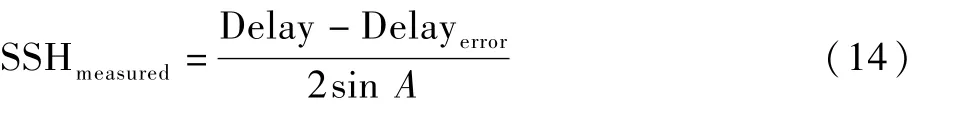
另一方面，通過TDS-1數據中提供的GPS衛星與TDS-1衛星軌道數據，計算鏡面反射點位置，使用反演的海面高度SSHmeasured，與驗證模型計算出的海面高度SSHmodel進行對比作差，計算每個鏡面反射點的海面高度反演誤差ΔH，即

計算全部樣本的平均絕對誤差(Mean Absolute Deviation，MAD），以確定本文的高度反演精度。

式中：HMAD代表了全部樣本的MAD；n為樣本數量，且i＝1，2，…，n。

3.2 TDS-1反演結果分析

3.2.1 誤差模型驗證

對2.2節描述的誤差模型進行驗證，在實驗中隨機提取單個數據段進行海面高度反演，并將誤差修正前后的結果與DTU驗證模型對比。圖7為誤差處理前后的結果對比示例。其中，紅線為該段海域的DTU驗證模型的高度，藍線為海面高度初步反演結果，黃線為修正誤差后的海面高度反演結果。

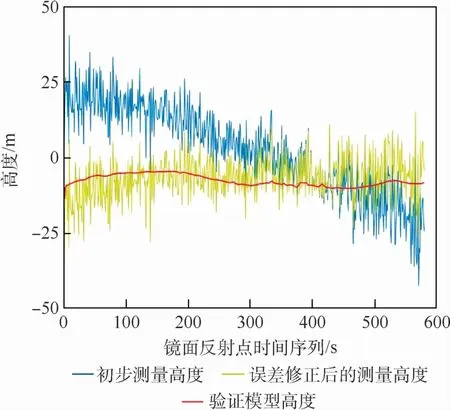
圖7 誤差修正前后的結果對比Fig.7 Comparison of results before and after error correction

在示例中，初步反演高度與DTU驗證模型的HMAD為13.5 m，修正誤差后的反演高度與驗證模型的HMAD為7.1 m。結果表明，通過上述方法有效修正了海面高度反演中存在的誤差。

3.2.2 區域海面結果

使用3.1節描述的方法，對南大西洋海域的數據進行計算，并將計算結果以經緯度1°為單位取平均。

圖8為反演得到的該區域的平均海面高度結果，圖9為對應的驗證模型高度。計算測量結果與DTU驗證模型結果的HMAD，得到的初步反演精度約為12.8 m，進行誤差修正后，精度約為7.3 m。

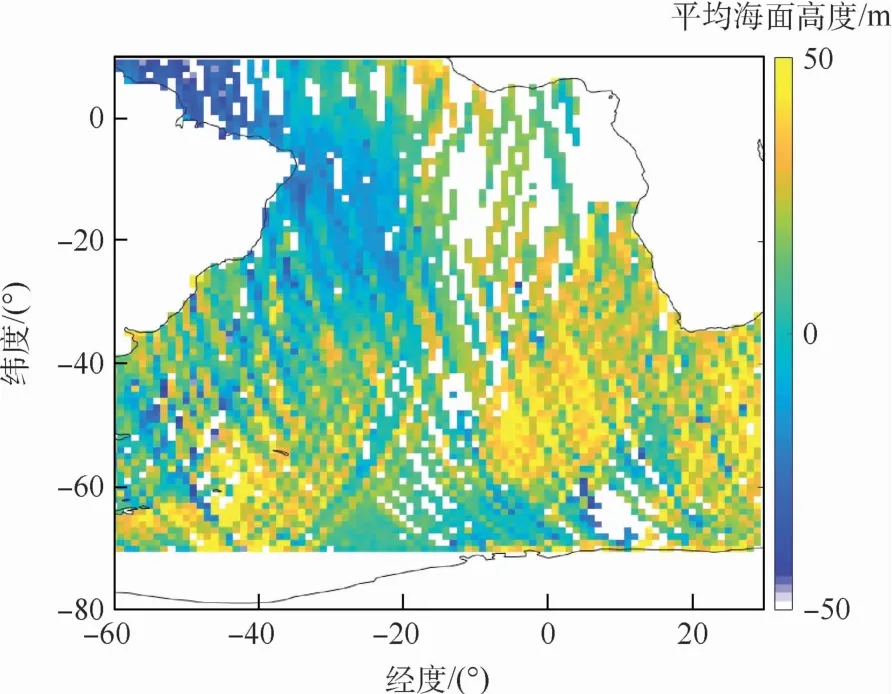
圖8 測量的平均海面高度(南大西洋海域）Fig.8 Mean sea surface height measurement(South Atlantic）

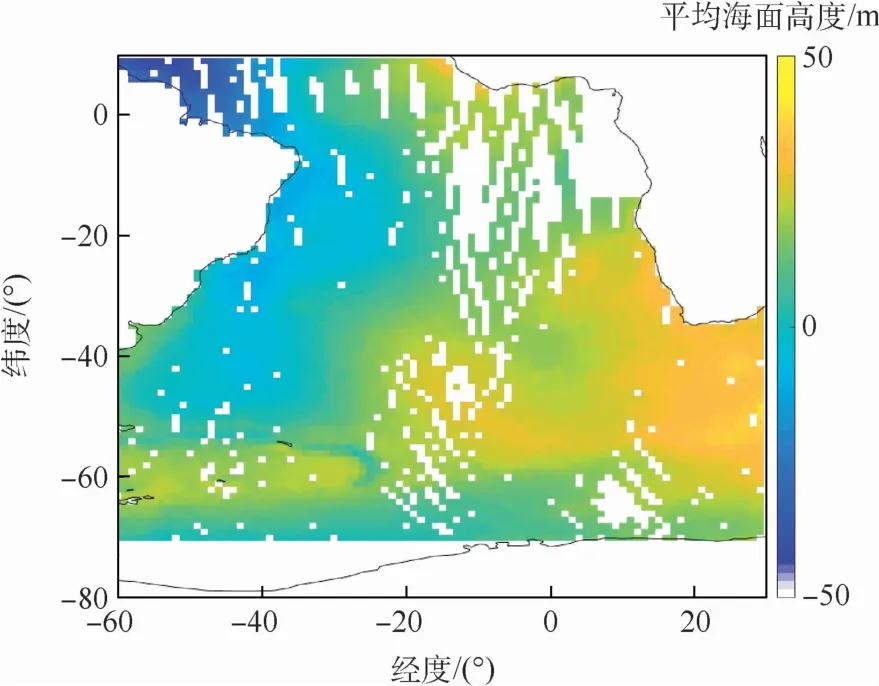
圖9 驗證模型的平均海面高度(南大西洋海域）Fig.9 Mean sea surface height of verification model(South Atlantic）

該區域的測量結果驗證了本文使用的誤差修正方法對星載GPS-R海面高度反演模型修正的可行性，可以用該方法對全球的數據進行處理并進行精度驗證。

3.2.3 全球海面結果和精度分析

本文使用的TDS-1數據的時間范圍為2018年4月10日至2018年4月30日，觀測數據約200萬個，使用3.1.1節提到的方法進行數據篩選，得到滿足條件的數據約為80萬個。在數據計算后，篩除數據結果中的明顯異常點(式(15）中的海面高度反演誤差ΔH絕對值大于100 m）。

得到海面高度計算結果后，將結果以經緯度1°為單位進行平均，得到每經緯度的平均海面測量高度，并計算對應的DTU驗證模型高度。測量所得到的海面高度與驗證模型海面高度在全球范圍內呈現出一致性。對總體結果進行分析，計算全部樣本的HMAD，其中誤差修正前的HMAD為8.52 m，誤差修正后的HMAD為6.05 m。

3.2.1 節是單個數據段的結果，沒有經過平均計算，3.2.2節是區域海面的1°平均結果，3.2.3節是全球海面的1°平均結果。由于計算方法(是否采用平均算法）和樣本數量不同(區域海面樣本數約為12萬，全球海面樣本數約為80萬），在誤差修正前后MAD及相應的提升精度差別較大。

本文著重將全球海面的測量結果與驗證模型結果的MAD進行統計。如圖10所示，統計結果接近正態分布，誤差修正前，有64.77%的數據觀測精度處于－20～20 m間，誤差修正后的數據中有80.89%的觀測精度處于－20～20 m。誤差主要來源于接收機軌道的不準確性、系統誤差和電離層模型誤差等。在處理接收機軌道誤差時，模型建立仍會出現一些新的誤差；并且在實驗中，信噪比和天線增益對精度的影響也極為明顯，這些問題導致了系統誤差的出現。本文使用的是HALF方法，該方法是對海面長期觀測的經驗模型，是對大量粗糙海面所造成的漫反射情況進行分析所建立。因此，HALF方法并不完美適用于所有海域，會產生由該模型引起的誤差。同時，本文使用的電離層模型基于IRI2016模型，IRI2016模型的誤差會對電離層延遲造成影響，引起電離層模型誤差。為防止修正過度，本文中天基線姿態誤差預估的比理論實際值小，且TDS-1衛星在運動中會造成天基線姿態的不確定性，該不確定性會導致天基線姿態誤差的不規則變化。在研究中發現，測量結果與驗證模型存在著固定誤差，出現固定誤差的原因及補正方式需要進一步的研究。

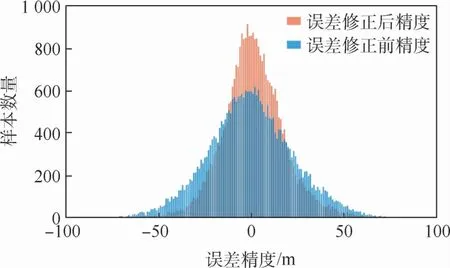
圖10 反演得到的全球平均海面高度誤差統計Fig.10 Error statistics of global average sea surface height obtained by retrieval

4 結束語

星載GPS-R的海面高度反演的研究剛剛起步，國內外相對于海面高度反演的研究較少，作為被動接收遙感的星載GPS-R技術具有低成本和全球范圍監測等優點，在海面高度反演領域有很大的發展前景。

本文在機載GPS-R海面高度反演的研究基礎上，結合星載GPS-R海面高度反演的可行性，研究了星載GPS-R海面高度反演模型，并將反演模型中的各類誤差進行了分析，找到各類誤差產生的具體原因及修正方法，建立了誤差模型，提高了星載GPS-R海面高度反演精度。本文使用了TDS-1衛星的約200萬個數據(篩選后實際使用約80萬個數據）進行海面高度反演實驗，反演結果與DTU驗證模型對比，誤差修正前的海面高度反演的平均絕對誤差約為8.52 m，誤差修正后的海面高度反演的平均絕對誤差約為6.05 m，提升了約2.47 m精度。結果表明，本文使用的誤差模型修正的星載GPS-R海面高度反演模型能夠較準確地反演全球海面高度。

由于TDS-1數據主要用途并非海面高度反演，衛星接收機并未對高度反演進行優化，對高度反演精度造成了限制。未來可通過繼續優化重跟蹤算法，使用針對海面高度反演的衛星接收機等方式對星載GPS-R 海面高度反演的精度進行提升。

致謝感謝MERRByS網站提供的TDS-1數據，IGS網站提供的SP3精密軌道文件，以及丹麥技術大學提供的DTU全球海潮模型和DTU全球平均海面模型。感謝北京航空航天大學的楊東凱教授和CSIC-IEEC的李偉強博士在GNSS-R星載數據分析中提供的建議。感謝上海航天電子技術研究所的周勃工程師和秦瑾博士對于反射信號接收機方面提供的建議。