考慮負荷不平衡分布的低壓配電網線損實用計算策略

劉科研，賈東梨，王薇嘉，耿光飛，魏琛豪

（1.中國電力科學研究院有限公司，北京 100192；2.中國農業大學 信息與電氣工程學院，北京 100083）

0 引言

低壓配電網線制復雜，三相不平衡情況普遍存在［1］。三相不平衡會引起三相電壓和電流不對稱，而且使中性線上產生電流，進一步加大了線路損耗［2—4］。

低壓配電線路結構多為輻射狀分布，同等大小的負荷，距離變壓器二次側越遠，造成的損耗越大；不平衡程度相同的三相負荷組合，距離變壓器二次側越遠，造成的損耗越大［5］。因此，在計算三相四線制的低壓配電網線損時,應該同時考慮負荷分布與三相不平衡。

目前，低壓配電網易獲取的數據還不足以進行大規模的潮流計算或者智能算法計算，因此電力行業標準DL/T 686-2018《電力網電能損耗計算導則》［6］中要求，0.4 kV低壓電力網的電能損耗計算宜采用等值電阻法、分相等值電阻法和臺區損失率法。該類方法對數據的類型和數量要求較低，但存在假設條件多，考慮因素不充分，結果誤差較大等問題。文獻［7—9］對傳統線損計算方法的模型和適用范圍進行了介紹。文獻［10］以負荷用電量為數據對等值電阻法進行了改進，考慮了三相不平衡因素。文獻［11］忽略沿線電壓降落時，可以由基爾霍夫電流定律和對稱分量法得到每條線段電流，計算三相不平衡時的線損。文獻［12］在復功率相同的情況下比較平衡與不平衡時的線路損耗，以變壓器出口側不平衡度計算線路總不平衡損耗。這些方法考慮了三相不平衡對線損的影響，較之傳統計算方法精確度得到了一定的提升，但對不平衡程度與線損的定量關系不明確，以線路首端不平衡度衡量整個臺區的不平衡情況，忽略了負荷分布不平衡對線損的影響，存在理論誤差。

文獻［13］定性分析了負荷、線路參數和分布式電源（distributed generation,DG）接入對不平衡度的影響，但沒有更進一步，研究多種因素通過影響不平衡度對線損的影響。文獻［14］分析了接入DG產生的負荷空間分布變化對線損的影響；文獻［15］考慮動態三相不平衡度，以線路結構為基礎，計算損耗在各支路的分布情況；上述文獻考慮了多種線損影響因素，但沒有就負荷空間分布的不平衡與線損之間的相關性進行分析。

本文提出一種考慮負荷分布不平衡的線損計算方法。以易獲取的有功電量數據為基礎，基于前推法構建考慮負荷分布不平衡的線損計算模型和考慮負荷分布的不平衡修正系數模型，量化負荷分布與線損的相關性；通過理論分析和數學推導將模型進行等效簡化，提出一種考慮負荷分布的線損計算方法。最后，通過算例驗證本文所提方法的合理性。

1 考慮三相不平衡的低壓配網線損計算

1.1 三相負荷不平衡對低壓配電網線損的影響

以式（4）為基礎可以確定η，進而得到ΔA′L。

1.2 三相不平衡時的線損計算模型

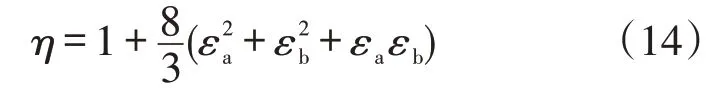
因此，當中性線線徑與相線相等或為相線1/2時，負荷集中在某一相的線損分別為平衡時的6倍和9倍。

2 考慮負荷分布的平衡態線損計算

目前低壓臺區線損相關數據的數據質量不高，因此本文以各負荷點電量數據為基礎進行分析計算，此數據可信度較高，且不需要增加采集成本。

2.1 集中負荷下的平衡態線損計算模型

2.2 考慮負荷分布的平衡態線損計算模型

低壓配電線路運行時網絡結構一般如圖1所示。

設饋線上負荷有功用電量沿饋線長度x的分布函數為AP(x)。當饋線上所帶負荷節點數m趨近于無窮時，可將式（17）中的求和公式進一步用積分形式表示如下

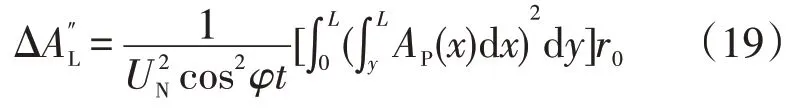
2.3 4種典型負荷分布的線損計算模型

負荷有功用電量沿線分布模式多樣，列出4種典型分布進行分析，包括：末端集中分布、均勻分布、遞減分布、遞增分布。4種分布函數AP(x)及相應曲線如圖2所示，以線路首端作為橫坐標的原點。

分別將4種典型分布的分布函數代入式（19）中，可推導出4種典型負荷分布的線損計算模型。

不同情況的分布函數與線損修正系數見表1。

修正系數ξ負荷分布末端集中1連續均勻1/3連續遞減1/5連續遞增8/15

實際線路負荷點有限，負荷分布為離散點分布，因此與表中數值相比存在一定誤差。設實際負荷數為M，ξ′隨M的增大而減小，M=10時各種情況的最大誤差約5%。

負荷數大于10的負荷離散分布與連續分布的修正系數誤差約為5%，因此，在可獲取數據有限或對計算精度要求不高時，負荷離散分布可以近似等價于負荷連續分布，方便進行后續分析計算。

3 考慮負荷分布三相不平衡的線損分析

由于單相負荷的存在和各相負荷空間分布的不同，存在線路首端三相接近平衡，但沿線三相不平衡程度較高的情況。因此，三相不平衡與負荷分布對線損的影響存在相關性。本文在目前可利用數據源的基礎上定量分析負荷分布，建立一種考慮負荷分布三相不平衡的線損計算模型；設定與實際情況較為匹配的兩類場景（首端平衡并考慮負荷分布、首端不平衡但三相負荷同分布）對模型進行簡化分析，提出適用于常見場景的線損計算方法，提高方法的適用性。

3.1 考慮負荷不平衡分布的線損計算模型

現假設三相負荷用電量沿線路的分布可分別表示為函數APa(x)、APb(x)、APc(x)。當饋線上所帶負荷節點數m趨近于無窮時，可設求和公式進一步用積分形式表示為

式（24）定義的ω修正了兩部分損耗：考慮負荷分布的線損及三相不平衡附加損耗。

3.2 首端平衡負荷不平衡分布的線損估算方法

在電網規劃與運行中，為了降低損耗，總是盡可能使低壓線路首端實現三相平衡，因此定量分析此類情況下負荷分布對線損的影響具有重要實際意義。本節以4種典型分布為基礎，推導出16種首端平衡而各相負荷不同分布時的線損修正系數，進而給出此類場景的線損估算方法。設饋線上各相負荷首端總有功用電量為APa、APb、APc，APa=APb=APc=APL/3，中性線線徑為相線的1/2，即RN=2 R。

以A相為末端集中分布，B相為均勻分布，C相為遞增分布為例進行分析。

三相負荷分布函數，如下所示

由4種典型分布構成的三相分布不完全相同的情況有16種，三相同分布有4種。此20種分布的線損修正系數ω及其估算值ω′，如表2所示。

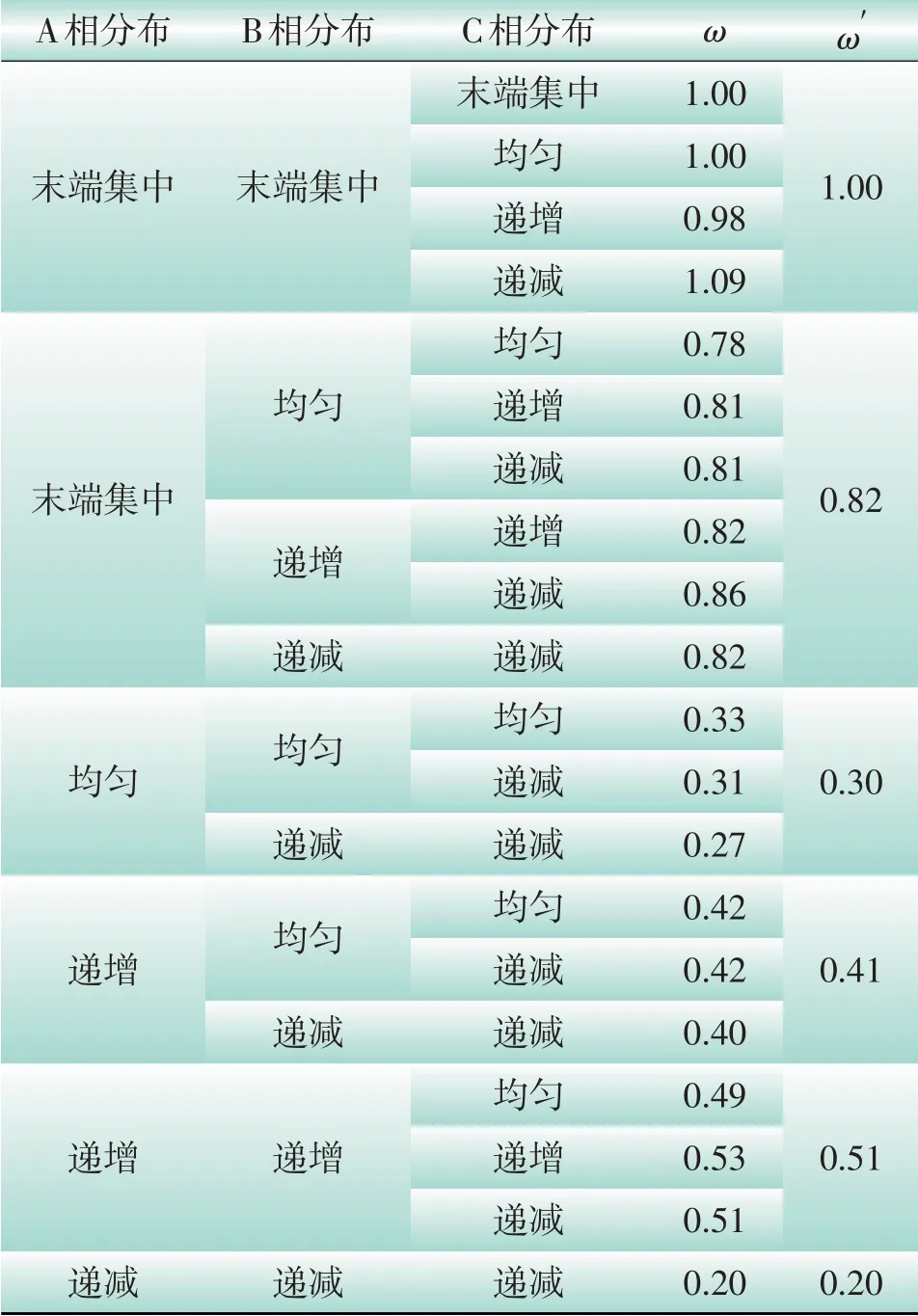
A相分布末端集中末端集中均勻遞增遞增遞減B相分布末端集中均勻遞增遞減均勻遞減均勻遞減遞增遞減C相分布末端集中均勻遞增遞減均勻遞增遞減遞增遞減遞減均勻遞減遞減均勻遞減遞減均勻遞增遞減遞減ω 1.00 1.00 0.98 1.09 0.78 0.81 0.81 0.82 0.86 0.82 0.33 0.31 0.27 0.42 0.42 0.40 0.49 0.53 0.51 0.20 ω′1.00 0.82 0.30 0.41 0.51 0.20

由表1可以看出，上述20種負荷分布情況按ω大小可大致分為6類。

3.3 首端不平衡但三相負荷同分布時的線損估算方法

當首端三相總負荷不等時，式（23）依然成立。若三相負荷同分布，則每個負荷點三相不平衡修正系數相同，此時的線損計算如下

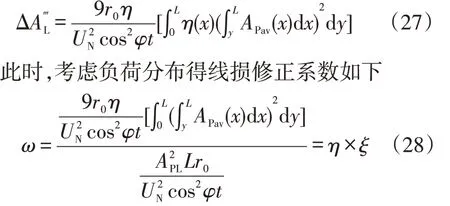
由式（28）可知，首端不平衡但三相同分布的線損修正系數ω為首端三相不平衡修正系數η與負荷分布修正系數ξ的乘積。

將表1中的修正系數ξ代入式（28）可得首端不平衡三相同分布時的線損修正系數ω，如表3所示。

負荷分布形式末端集中分布均勻分布遞增分布遞減分布損耗修正系數ω η η/3 8η/15 η/5

4 結束語

本文以較易獲取的有功電量為數據源，提出一種考慮負荷分布的低壓臺區三相負荷不平衡分布線損計算方法。首先，建立負荷集中分布的三相負荷不平衡分布線損修正系數模型，通過前推法，建立負荷三相平衡、同分布的理論線損計算模型，進而提出一般情況下考慮三相負荷不平衡分布的線損計算方法。為了便于應用，以4種典型分布為基礎，通過數學推導和理論分析，提出適用于兩類典型場景（首端平衡且三相不同分布、首端不平衡且三相同分布），考慮三相負荷不平衡分布的線損估算方法。算例結果表明，本文提出的方法能夠在已知臺區首端各相負荷用電量和負荷分布規律時較為準確地計算臺區線損，提高理論線損計算精度，為不平衡治理和臺區經濟運行提供可靠參考依據。本文的研究主要針對負荷的不平衡分布，尚未考慮由線路長度等因素導致的三相網絡不平衡，下一步工作主要針對上述不足進行研究，進一步完善不平衡情況下的線損計算策略。D