橢圓與兩焦點弦有關的幾個重要性質及其推論

山東省鄒平雙語學校(256200) 姜坤崇

我們把過圓錐曲線焦點的弦稱為它的焦點弦,焦點弦是圓錐曲線中的重要線段,許多性質都與它有關. 本文給出橢圓與兩條滿足一定條件的焦點弦有關的幾個重要性質及其推論. 由于橢圓具有軸對稱性,因此以下對于只涉及一個焦點的結論,不失一般性,我們均設焦點弦為左焦點弦.

定理1給定橢圓E:= 1(a ＞b ＞0),AB、CD是過E左焦點F1(-c,0)(c=以下同)的兩條互相垂直的弦,則為定值

證明(1) 如圖1, 當AB不為E的長軸和垂徑(過焦點且垂直于焦點軸的弦) 時,CD亦不為E的長軸和垂徑,設A(x1,y1),B(x2,y2),直線AB、CD的斜率分別為k1、k2, 則直線AB、CD的方程分別為y=k1(x+c)、y=k2(x+c), 將y=k1(x+c) 代入E的方程整理得(a2k21+b2)x2+2a2ck21x+a2(c2k21-b2)=0.

圖1

由于x1,x2為以上關于x的二次方程的兩個根,故由韋達定理得x1+x2=所以,

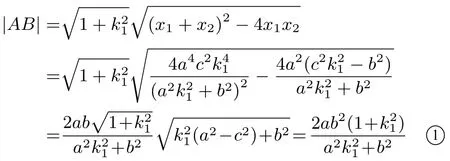
同理,

由于AB⊥CD,故k1k2=-1(k1k2/= 0),從而k21k22=1,于是

(2)當AB為E的長軸(垂徑)且CD為E的垂徑(長軸)時,不難驗證亦成立,從略.

綜合(1)、(2),定理1 得證.

推論1如圖2,給定橢圓=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,AB、CD分別是E過F1、F2且互相垂直的弦,則為定值

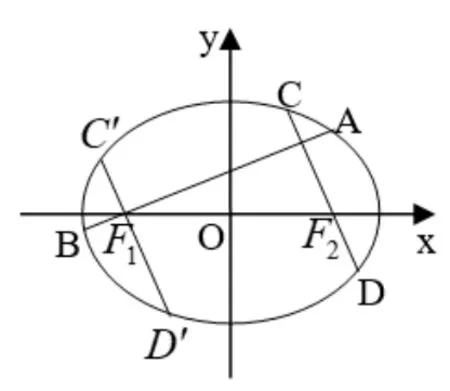
圖2

證明過F1作與CD平行的弦C′D′,則由橢圓的中心對稱性知|C′D′|=|CD|,又由AB⊥CD得AB⊥C′D′,于是由定理1 的結論知

推論2如圖3,給定橢圓E:=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,P是以F1F2為直徑的圓E1:x2+y2=a2-b2上異于F1、F2的任一點,直線PF1和PF2與E的交點分別為A、B和C、D,則為定值

圖3

證明由F1F2為E1的直徑知PF1⊥PF2,于是由定理1 推論1 的結論可得

推論3如圖4,給定橢圓E:=1(a ＞b ＞0),AB、CD是E的過左焦點F1(-c,0)的兩條弦,kAB·kCD=1(kAB、kCD分別為直線AB、CD的斜率,以下同)或AB、CD分別為E的長軸與垂徑, 則為定值

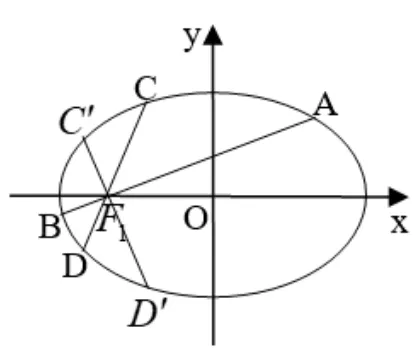
圖4

證明當AB、CD有一條與x軸垂直(即AB、CD分別為E的長軸與垂徑) 時, 由定理1 知結論成立; 當AB、CD均不與x軸垂直時,作弦CD關于x軸的對稱弦C′D′,則由橢圓的軸對稱性知|C′D′|=|CD|,kCD=-kC′D′,kAB·kC′D′=-kAB·kCD=-1,從而AB⊥C′D′,于是由定理1 的結論知

推論4如圖5,給定橢圓=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,AB、CD分別是E過F1、F2的弦,kAB ·kCD=1 或AB、CD分別為E的長軸與垂徑,則為定值

圖5

證明當AB、CD有一條與x軸垂直(即AB、CD分別為E的長軸與垂徑) 時, 由定理1 知結論成立; 當AB、CD均不與x軸垂直時,作弦CD關于x軸的對稱弦C′D′,則由橢圓的軸對稱性知|C′D′|=|CD|,kCD=-kC′D′,kAB ·kC′D′=-kAB ·kCD=-1,從而AB⊥C′D′,于是由定理1 推論1 的結論知

推論5如圖6,給定橢圓=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,P是以F1、F2為兩頂點的等軸雙曲線E1:x2-y2=a2-b2上異于F1、F2的任一點, 直線PF1和PF2與E的交點分別為A、B和C、D,則

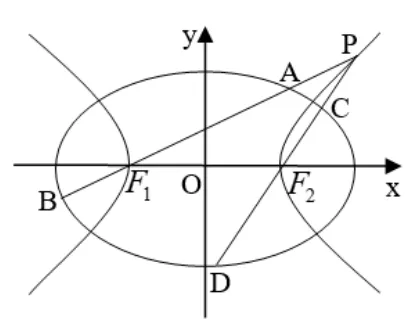
圖6

證明設P(x0,y0), 則由點P在E1上知x20- y20=a2-b2,即y20=x20-a2+b2,于是

說明以上由定理1 證明5 個推論所用的方法同樣適合于由下面的兩個定理證明其相應的推論,因此限于篇幅以下各定理的推論的證明均不再給出.

定理2給定橢圓= 1(a ＞b ＞0),AB、CD是E的過焦點F1(-c,0)的兩條弦,kAB ·kCD=或AB、CD分別為E的長軸與垂徑,則|AB|·|CD|為定值4b2.

證明(1)如圖7,當AB不為E的長軸和垂徑時,CD亦不為E的長軸和垂徑,設A(x1,y1),B(x2,y2),kAB=k1,kCD=k2,則直線AB、CD的方程分別為y=k1(x+c)、y=k2(x+c), 同定理1 的證明一樣得到①、②式. 因為k1k2=所以于是

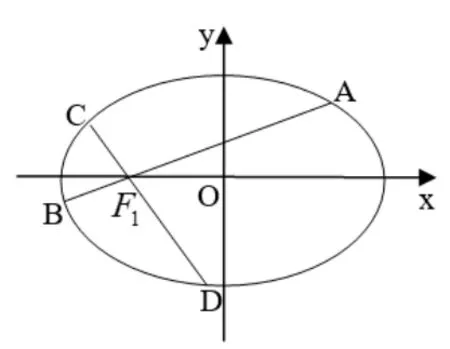
圖7

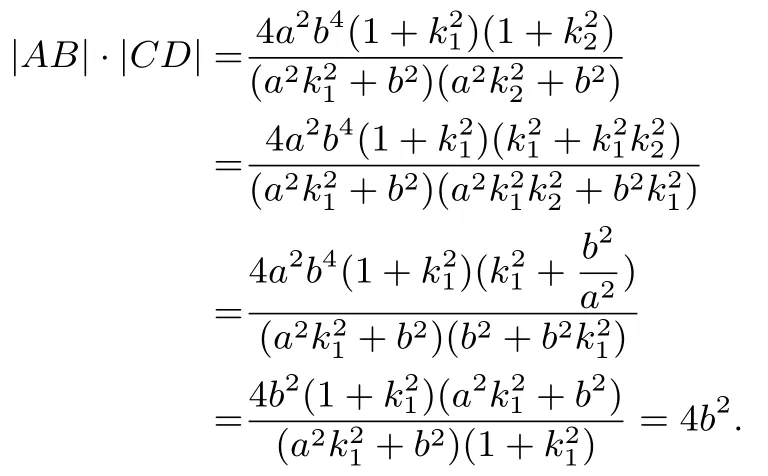
(2)當AB為E的長軸(垂徑)且CD為E的垂徑(長軸)時,不難驗證|AB|·|CD|=4b2亦成立,從略.

綜合(1)、(2),定理2 得證.

推論1給定橢圓E:= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,AB、CD分別是E過F1、F2的弦,kAB·kCD=或AB、CD分別為E的長軸與垂徑,則|AB|·|CD|為定值4b2.

推論2給定橢圓E:= 1(a ＞b ＞0),P是以E的兩個焦點F1、F2為頂點且離心率為的橢圓= 1(其中c2=a2-b2)上異于頂點的任一點,直線PF1和PF2與E的交點分別為A、B和C、D,則|AB|·|CD|為定值4b2.

推論3給定橢圓E:= 1(a ＞b ＞0),AB、CD是E的過焦點F1(-c,0)的兩條弦,kAB ·kCD=或AB、CD分別為E的長軸與垂徑, 則|AB|·|CD|為定值4b2.

推論4給定橢圓E:= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦點,AB、CD分別是E過F1、F2的弦,kAB·kCD=或AB、CD分別為E的長軸與垂徑,則|AB|·|CD|為定值4b2.

推論5給定橢圓E:= 1(a ＞b ＞0),P是以E的兩個焦點F1、F2為頂點且離心率為的雙曲線=1(其中c2=a2-b2)上異于頂點的任一點,直線PF1和PF2與E的交點分別為A、B和C、D,則|AB|·|CD|為定值4b2.

定理3給定橢圓E := 1(a ＞b ＞0),AB、CD 是E 的過焦點F1(-c,0)的兩條弦,kAB·kCD=或AB、CD 分別為E 的長軸與垂徑,則|AB|+|CD|為定值

證明(1) 如圖8, 當AB不為E 的長軸和垂徑時,CD亦不為E 的長軸和垂徑, 設A(x1,y1),B(x2,y2),kAB=k1,kCD= k2, 則直線AB、CD 的方程分別為y =k1(x + c)、y = k2(x + c), 同定理1 的證明一樣得到①、②式.

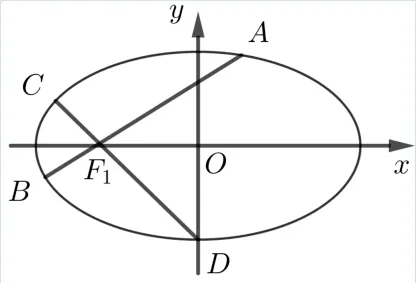
圖8

因為k1k2=(k1k2/=0),所以k21k22=于是

(2)當AB 為E 的長軸(垂徑)時,CD 為E 的垂徑(長軸),不難驗證|AB|+|CD|=亦成立,從略.

綜合(1)和(2),定理3 得證.

推論1給定橢圓= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E 的左、右焦點,AB、CD 是E 的分別過F1、F2的弦,kAB·kCD=或AB、CD 分別為E 的長軸與垂徑,則|AB|+|CD|為定值

推論2給定橢圓E :=1(a ＞b ＞0),P 是以E 的兩焦點F1、F2為長軸的兩端點且與E 同離心率的橢圓E1:=1(其中c2=a2-b2)上異于F1、F2的任一點,直線PF1和PF2與E 的交點分別為A、B 和C、D,則|AB|+|CD|為定值

推論3給定橢圓E := 1(a ＞b ＞0),AB、CD 是E 的過焦點F1(-c,0)的兩條弦,kAB·kCD=或AB、CD 分別為E 的長軸與垂徑,則|AB|+|CD|為定值

推論4給定橢圓E := 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E 的左、右焦點,AB、CD 分別是E 過F1、F2的兩條弦,kAB·kCD=或AB、CD 分別為E 的長軸與垂徑,則|AB|+|CD|為定值

推論5給定橢圓E := 1(a ＞b ＞0),P 是以E 的兩焦點F1、F2為頂點且離心率為為E 的離心率)的雙曲線= 1(其中c2= a2-b2)上異于頂點的任一點,直線PF1和PF2與E 的交點分別為A、B 和C、D,則|AB|+|CD|為定值