別出心裁建系 標新立異設點

浙江省蘭溪市第一中學(321102) 張城兵

1 問題的提出

自從引入向量法,立體幾何解答題似乎談不上難題,這一觀點在早些年有點道理,但現在再以這種眼光看,似乎有失偏頗,因為從近幾年浙江省高考題(第2 個解答題)來看不簡單,很多考生出師不利,從此題產生沮喪的心情直到考試結束. 有網友說要在模擬卷或高考卷中出些用向量法無從下手的題目. 盡管這種說法與《普通高中數學課程標準(2017年版)》的要求相背離,但也不得不警惕、提防用向量法解有點棘手的題目. 事實上,在高考或平時練習中,有很多題目對空間想象力要求很高,在短時間內用傳統方法做好這種題有難度,對空間想象力較弱的學生更是一種痛苦的折磨,所以在有限的考試時間內勢必快速轉向求助于向量法,這就要求向量法掌握得比較嫻熟,才能行走江湖. 如何讓高三學生掌握向量法,最大可能一招制勝呢? 教學實踐表明: 在圖形不是“很正統”的情形下,培養學生巧建系、妙設點的能力很重要. 這一能力的培養就相當于讓他們掌握核心技術,為破解難題提供方便. 為此筆者收集整理了一些“帶刺”的試題,結合學生解題的成敗得失給讀者一點啟示,同時限于篇幅,其它簡單的方法不再贅述.

2 精選例題,妙法剖析

例1如圖1,棱長為3 的正方體的頂點A在平面α上,三條棱AB,AC,AD都在平面α的同側. 若頂點B,C到平面α的距離分別為1,則頂點D到平面α的距離h=____,頂點E到平面α的距離為____.

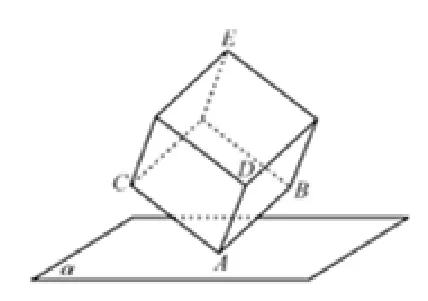
圖1

解析建立如圖2 所示的空間直角坐標系, 設平面α的法向量為n= (x,y,z), 易得B(3,0,0)、D(0,0,3)、C(0,3,0)、E(3,3,3), 則dB== 1,整理得求得y2= 2x2,z2= 6x2. 所以dD=

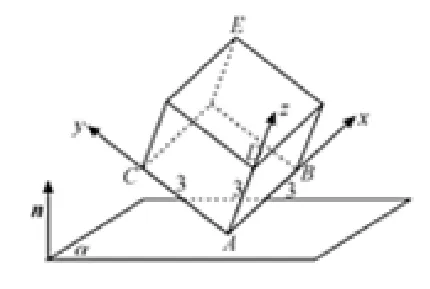
圖2

評注此題的建系打破以α平面為xoy平面建系的常規思路,同時也告訴我們無論“墻角”如何放,都不影響問題的解決,不要受無關因素的干擾.

例2如圖3,正四面體A-BCD的棱CD在平面α上,E為棱BC的中點,當正四面體A-BCD繞CD旋轉時,直線AE與平面α所成最大角的正弦值為____.

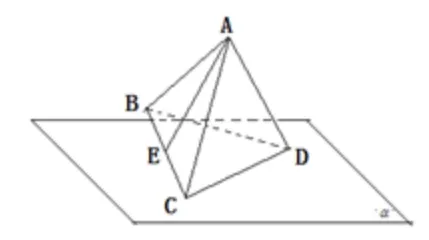
圖3

解析此題是在課外作業中出現, 筆者任教的兩個班答題正確率只有5%. 因為直線AE繞著異面直線CD動,而要求的是直線AE與平面α線面角的最大值, 若用傳統法做計算量是簡單的, 但對化歸能力要求高, 不是每個學生都能應對的. 若利用向量法, 大部分學生都能接受,并且這種處理問題方式能遷移其它地方應用. 為了建系方便, 可找出正四面體的“出生地”——正方體, 如圖4, 易求A(0,0,1),B(1,0,0),C(0,1,0),D(1,1,1),所以= (1,0,1). 令平面α的法向量為n= (x,y,z),又當正四面體ABCD繞CD旋轉時,利用相對運動,可理解為平面α繞CD旋轉,從而平面α的法向量始終垂直于CD轉動. 法向量作用是確定平面位置,與模長無關,為了計算方便特取模長為1. 所以x2+y2+z2=1,=x+z=0,消去z得,2x2+y2=1,由Cauchy不等式,得(3x+y)2=所以3x+y≤記直線AE與平面α所成角為θ,則故所求最大值

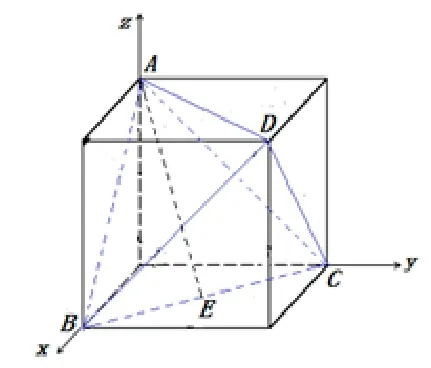
圖4

評注對立幾動態型問題,學生最怕的是圖形變化中無法度量的有關幾何量的處理,也就無法轉化為用“數”來定量計算了,而建系后用上坐標就自然讓“動態的形”和有關變量融合在一起,相比較而言,代數運算求最值學生掌握得好些.

例3(2020年10 月浙南名校聯盟第一次聯考)如圖5,四棱錐P-ABCD中,面PBD⊥面ABCD,AB//DC,AB=2CD=4,AD=BC=

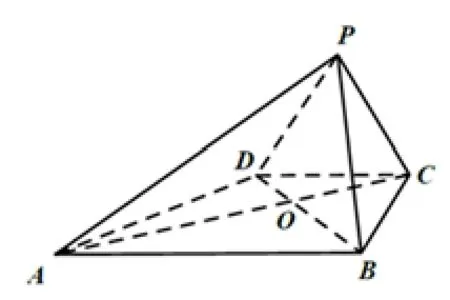
圖5

(1)證明PB⊥AC;(2)求直線BD與平面PBC所成角的正弦值.

解析據統計, 我校高三年級參考人數703 人, 第1 小題滿分8 分,平均得分6.484,第2 小題滿分7 分,平均得分2.044 分, 該題平均分為8.529 分. 特別實驗班103 人參考,該題平均分為12.176 分, 但第2 小題平均分只有4.294 分.通過分析, 發現有部分人對AC⊥BD證不起(與初中教材刪去“梯形”有關), 其次建立如圖6 坐標系后,P點坐標求不起,或者誤以為P點投影在原點O. 其實由面PBD⊥面ABCD,可知點P投影在y軸上,但不一定與O重合,故可設P(0,y,z),用AP=列方程組易求,或利用題設大量已知的線段,能精準求得P點坐標. 平面幾何功底欠缺的同學在求P點坐標時遇到阻礙就停滯了.

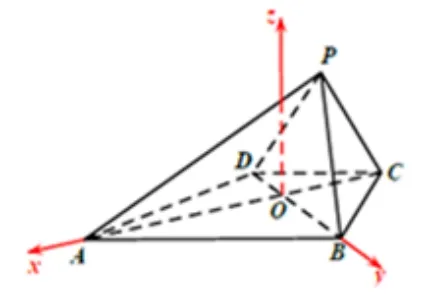
圖6

筆者另辟蹊徑,用如下方法:

由(1) 證明可知,PB⊥AC, 又由已知條件得,AP2+PB2=AB2, 所以PB⊥PA. 所以PB⊥面PAC, 所以PB⊥PC, 求得PC=從而又有AP2+PC2=AC2, 故PC⊥PA, 也即PA,PB,PC兩兩相互垂直,以P為原點建立如圖7 所示空間直角坐標系, 則平面PBC的法向量顯然為n= (1,0,0). 按照經驗, 再用方程組求D的坐標, 但鑒于此題特殊性, 可不求, 能節省大量時間,所以,

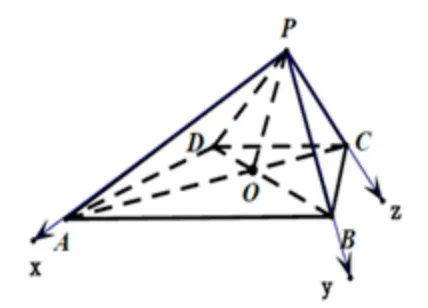
圖7

評注有“墻角”出現固然好,沒有就找“直角”. 利用幾何關系分步求點的坐標和用方程組求點坐標本質上是一致的,后者是減少動腦過程的一勞永逸“偷懶法”. 有時題設中出現平行線時,可用向量代換來巧妙回避求點的坐標.

例4如圖8,在矩形ABCD中,AB= 4,AD= 3,點E,F分別是線段DC,BC的中點,分別將ΔDAE沿AE折起,ΔCEF沿EF折起,使得D,C重合于點G,連接AF.

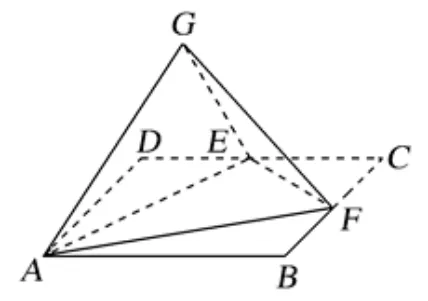
圖8

(1)求證: 平面GEF⊥平面GAF;

(2)求直線GF與平面GAE所成角的正弦值.

解析由(1) 證明可知GE⊥平面GAF, 并且發現∠AGF為鈍角(利用三邊長即可知), 所以以G為原點,GF,GE所在直線分別為y軸、z軸,讓x軸在平面AGF且在∠AGF內,建立空間直角坐標系,如圖9. 這樣好處就是點G恰好為原點,減少計算量,而唯獨A坐標不知道,但它在平面xGy內,豎坐標為0,列方程時能減少未知量.

圖9

令A(x,y,0),易求F(0,,0),E(0,0,2), 則由求得= (0,0,2),易求平面GAE法向量n=求得

評注如果以點C為原點,建立空間直角坐標系,再設G(x,y,z)也可做,但數據復雜得令人不勝其煩,這純屬意外,讀者不妨一試. 在實戰中確實是很難預測求某個點坐標及后期的運算復雜程度,同時告誡我們建系建在盡量讓待求坐標的點在xoy平面、xoz平面或yoz平面上,減少方程組個數,減輕運算量.

3 解法小結及感悟

(1)圖形中有“墻角”優先考慮,無論怎樣放置,不影響數量關系和位置關系;退而求其次,考慮圖形中的直角,如例3、例4.

(2)用到的點坐標能不求是上上策,因為求點坐標的目的是為了使用向量,若存在向量代換回避求點坐標是再好不過了.

(3)當所求關鍵點的投影在何處不知道時,就必須設點坐標(x,y,z),列方程組求解;若知道關鍵點的投影在某個坐標平面上,就可優化為2 個未知數,減少運算量. 列方程組不一定用線段長,垂直關系用向量數量積表示也能出現方程.

(4)在具體問題中建系設點還應統籌考慮,終極目標是為了運算量小,提高正確率.

4 測試的結果及分析

通過上述例題講授后,對兩個教學班測試了2020年高考浙江卷第19 題和2020 屆金華十校模擬第19 題,因為這兩道題都是讓2020 屆學生考試心情很不爽的“帶刺”試題,也是很有研究價值的試題. 分別制成小卡片,在筆者任教的2021 屆兩個班中測試教學效果和學生掌握鞏固程度,為了盡可能體現真實的水平,相鄰的同學測試題是不同的,15 至20分鐘后收回又換不同試題, 相當于每位同學都測試了兩題,但相鄰的同學始終題目不同,所以成績比較真實. 筆者沒有用評分細則,對不嚴謹的地方都不給滿分. 統計滿分率如下表:

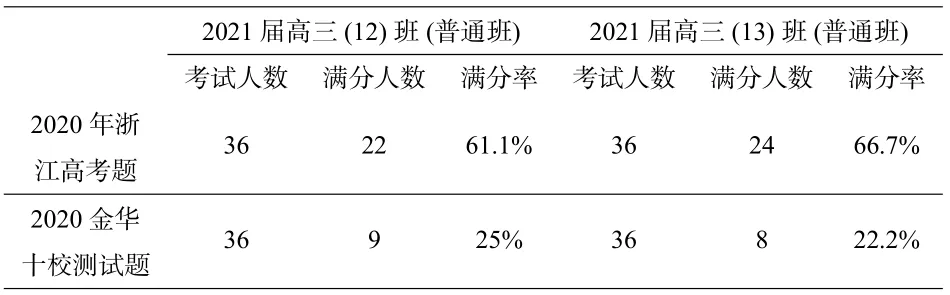
2021 屆高三(12)班(普通班) 2021 屆高三(13)班(普通班)考試人數 滿分人數 滿分率 考試人數 滿分人數 滿分率2020年浙江高考題36 22 61.1% 36 24 66.7%2020 金華十校測試題36 9 25% 36 8 22.2%

筆者又查看了2020 屆學生當初針對測試題2 的答題情況(測試題1 滿分人數數據無法獲取),3 個實驗班160 人,滿分人數是6 人,普通班634 人,沒有人滿分. 一對比,筆者對任教學生掌握程度很滿意,對學生精彩解法展示如下:

測試題1(2020年高考浙江卷第19 題)如圖10,三棱臺DEF-ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC=2BC.

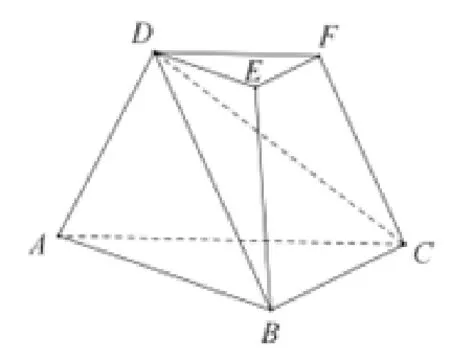
圖10

(I)證明:EF⊥DB;

(II)求DF與面DBC所成角的正弦值.

學生建系用得非常溜,網上出現的或期刊發表的各種解法都有出現,筆者對下面出自中等生之手的解法(截止投稿前,筆者沒有看到過有此解法)大為欣賞:

如圖11, 以點C為原點,CA所在直線為y軸, 在平面ABC上過C且垂直于CA的直線為x軸, 過C垂直平面xCy直線為z軸, 建立空間直角坐標系, 令BC=則CD=因為∠ACB= ∠ACD= 45°,所以D(0,2,2),B(1,1,0), 所以(1,1,0),由已知三棱臺易知= 0,所以CB ⊥DB,即EF⊥DB.

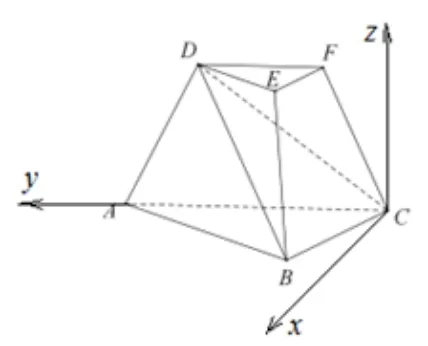
圖11

測試題2(2020年4 月金華十校聯考第19 題)如圖12,在四棱錐C -ABNM中, 四邊形ABNM的邊長均為2,ΔABC為正三角形,MB=MB⊥NC,E,F分別為MN,AC的中點. (1)求證:MB⊥AC;(2)求直線EF與平面MBC所成角的正弦值.

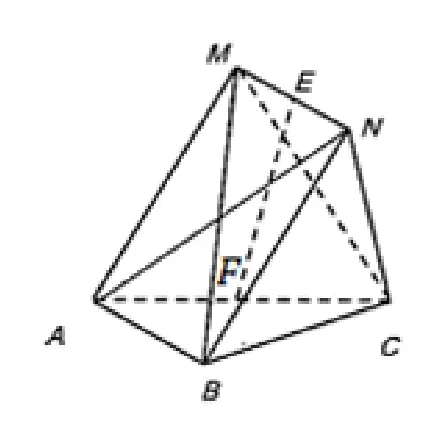
圖12

有很多同學想到以點F為原點建系,但問題出在設好點M(x,y,z),找不齊三個方程就擱淺了,也有同學直接讓z軸過FM,歪打正著,還有一部分同學憑著扎實的平面幾何功底證明點F是“墻角”,也能順利解得. 另外N的坐標不知道,也給解題帶來很大困難,但很多同學巧妙回避了求N的坐標,掌握了解題要領. 相比而言,也有一半少點同學采用方法二,頗具特色,但數據繁雜一些,導致計算頻頻出錯,所以建系前要評估一下在平面xoy上盡可能使點的坐標為整數,少出現分數和無理數.

方法一以FB、FA分別為x軸和y軸,建立空間直角坐標系如圖13,則易求A(0,1,0),C(0,-1,0),設M(x,y,z),則

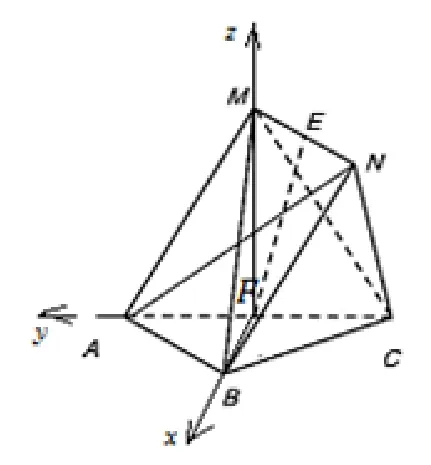
圖13

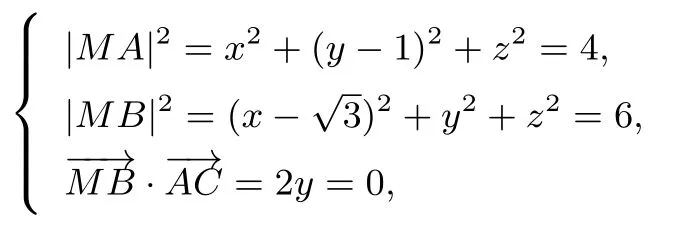
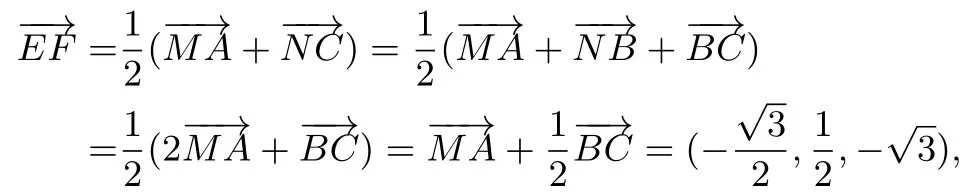
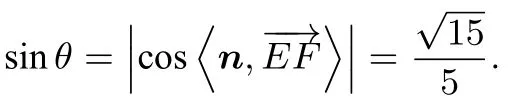
方法二由(1)證明可知MB⊥面ACN,從而面ACN⊥面ABNM, 記MB與AN的交點為H, 又易知四邊形ABNM為菱形, 所以以HA、HB所在直線為x軸,y軸,過H在平面ACN中作垂直AN直線為z軸, 建立空間直角坐標系, 如圖14. 易求

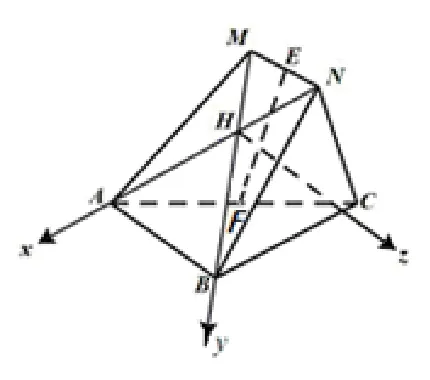
圖14

令C(x,0,z),由

求得x=,z=所以求得進而求得平面MBC的法向量為所以sinθ= 所以求得直線EF與平面MBC所成角的正弦值

讀者朋友不妨用坐標法試做下面一題:

如圖15,在斜三棱柱ABC-A1B1C1中,側面AA1C1C是菱形,AC1⊥B1C1,AC1與A1C交于點O.

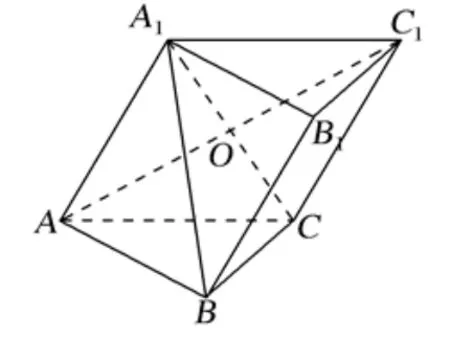
圖15

(1)求證:AO⊥A1B;

(2) 已知∠BA1C= 30°,2AC1= 3A1C, 求二面角A-A1B-C的正切值.(答案: 3.)

5 結束語

綜觀上述4 例及測試題,呈現出向量方法的多姿多彩及其獨特的魅力, 感悟向量是研究空間幾何問題的有力工具.但在用向量法解題時,必須了解空間向量基本定理,充分掌握空間向量的正交分解及其坐標表示,掌握對空間向量加、減、數量積運算及其坐標表示,夯實基礎,才能做到“手中有糧,心中不慌”,不然,很容易“盲人騎瞎馬,夜半臨深池”. 還有一點,初中平面幾何功底欠缺的同學對第1 小題都感到力不從心,那么第2 小題用向量法也不會一帆風順,畢竟第1 小題是屬于前期勘察地形地貌,為后面建系設點提供便捷,所以我們在復習立體幾何過程中,還要補上初中里削弱的或刪除的平面幾何內容,如梯形中的常用輔助線和等腰梯形的性質(浙江省初中數學教材中沒有“梯形”這一章節). 針對本班情況,有時哪種方法學生難以施展,筆者講評時側重用哪種方法,培養學生解立體幾何大題“文武雙全”的本領.