具有時變時滯的多智能體系統的加權平均一致性
張鐵成,劉云芬
(湖北師范大學 數學與統計學院,湖北 黃石 435002)
0 引言
近年來,多智能體網絡的分布式協調控制應用十分廣泛,而一致性是協調控制中的基本問題,具有重要的理論意義和實際應用價值。所謂一致性,就是多智能體系統在通過協調控制后,最終各個多智能體的狀態取得一致或相同。
關于多智能體系統的一致性問題已有一些研究成果。Olfati-Saber[1]提出了分散協調控制規則,以使多智能體無向網絡取得平均一致性,同時考慮了網絡存在通信時間延遲的情形。Lin等[2]采用LMI的方法,討論了時變時滯網絡的平均一致性問題。楊繼永等[3]利用馬爾可夫收斂準則探討了多智能體系統平均一致性問題。宋莉等[4]利用模型變換方法研究了具有不確定拓撲及聯合連通圖的多智能體網絡的平均一致性。康玉婷等[5]開展了具有隨機切換拓撲結構的多智能體系統平均一致性的研究。孫一杰等[6]利用輔助變量方法解決了多智能體網絡在任意強連通下平均一致性問題。Meng等[7]基于無向圖研究了一階多智能體系統在固定和切換拓撲下的周期事件觸發平均一致性問題。Wang等[8]采用事件觸發控制的方法討論了存在常通信時滯的多智能體系統的平均一致性問題。李富強[9]研究了事件觸發機制下具有固定和切換拓撲結構的多智能體網絡的平均一致性問題。韓世濤等[10]采用周期采樣和事件控制的方法對多智能體系統的事件觸發平均一致性問題進行了時滯魯棒性分析。還有一些其他類似的研究成果[11~15]。
目前,大多數多智能體網絡一致性的成果僅限于系統收斂值為初始值的平均值(平均一致性)的情形,本文提出一種新的控制協議,能夠使智能體的狀態最終能達到任意的加權平均值(加權平均一致性),并且系統是在切換拓撲結構并伴隨著時變時滯的情形下實現的。同時,考慮到在系統穩定性分析中代數方法的復雜性,本文引入正交變換,將奇異系統矩陣轉化為非奇異系統矩陣,使系統收斂條件化簡為LMI的可解性問題。
1 預備知識
1.1 代數圖論
設G(V,E,A)表示頂點集為V,邊集為E,權重鄰接矩陣為A的權重有向圖。圖的每個結點表為Vi∈V或i∈I={1,2,…,n};圖的每條邊表示為e=(νi,νj);權重鄰接矩陣A=[aij],aij>0,且對任意的i∈I設aij=0.
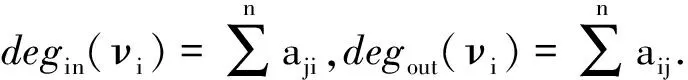
L=L(G)=D-A.由定義可知Laplacian矩陣每行之和為零,因此Laplacian矩陣總有屬于零特征值的右特征向量ω1=1n=(1,1,…,1)T.
定義1[1](強連通圖) 如果圖G的任意兩個頂點都存在一條路徑,則稱圖G為強連通圖。
定義2[1](平衡圖) 如果圖G的每個頂點的入度等于出度,則稱圖G為平衡圖。
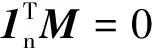
引理1[1]設G(V,E,A)為強連通圖,則圖G的Laplacian矩陣L滿足下列三條:
1)秩(L)=n-1;
2)矩陣L的一個特征值為0,相應的特征向量為1n,即L1n=0;
3)矩陣L除去一個為0的特征值以外的其他n-1特征值均有正實部。
1.2 一致性問題
設χi為第i智能體的狀態,每個多智能體的動態模型為:
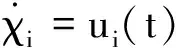
(1)
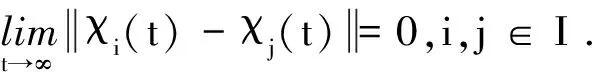
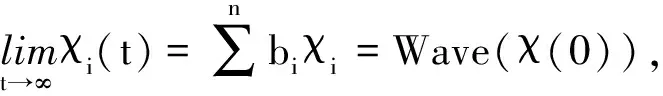
本文給出如下的控制協議:
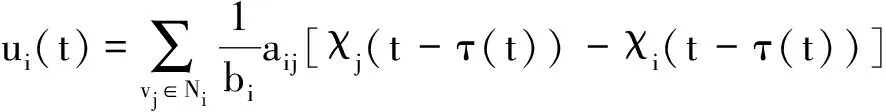
(2)
結合(1),多智能體系統的動態模型寫成矩陣的形式為
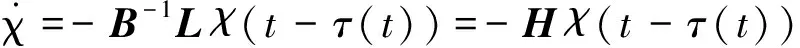
(3)

設映射st∶[0,+∞)→IΓ={1,2,…,N}(N∈+,指的是所有可能的有向圖的個數)是切換信號,它決定了網絡的拓撲結構。則在切換拓撲結構的網絡中(3)變為:
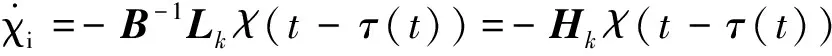
(4)
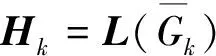
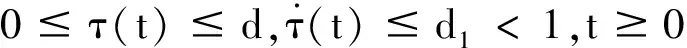
(5)
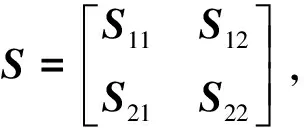
引理3[2]設矩陣

則以下三個命題成立:
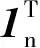
ii)存在正交矩陣F,使得下列等式成立
iii)正交矩陣F是矩陣Y的特征向量。對任何平衡矩陣J∈Rn×n,有

2 主要結論
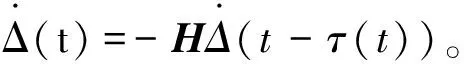

(6)
設FTΔ(t)=「δ(t),0?T,于是(6)可以寫為:
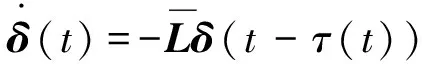
(7)
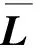

(8)
證明 我們定義如下的Lyapunov-Krasovskii函數:
沿著(7)的軌線,我們有:
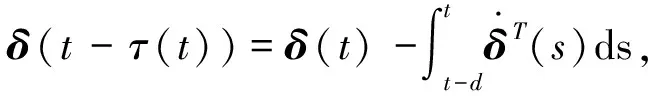
顯然,

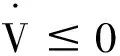

由引理2,可得(10)等價為
聯立(11),再利用引理2,即可得(8)。于是證明了當(8)成立時,系統(1)能取得全局漸進加權平均一致性。
定理2 考慮(5)條件下具有切換拓撲結構的有向圖G,G的n個結點的動態模型為(1),且G為強連通的平衡圖,則分散控制器(2)能取得全局漸進加權平均一致性,如果K∈IΓ,存在適當維數的對稱正定矩陣P,Q,R∈R(n-1)×(n-1)使得下面條件成立:
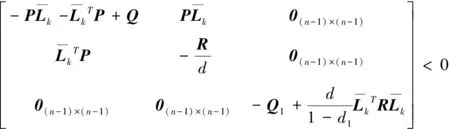
(12)
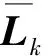
注:定理2的證明類似定理1的證明,這里省去。
3 例子和仿真
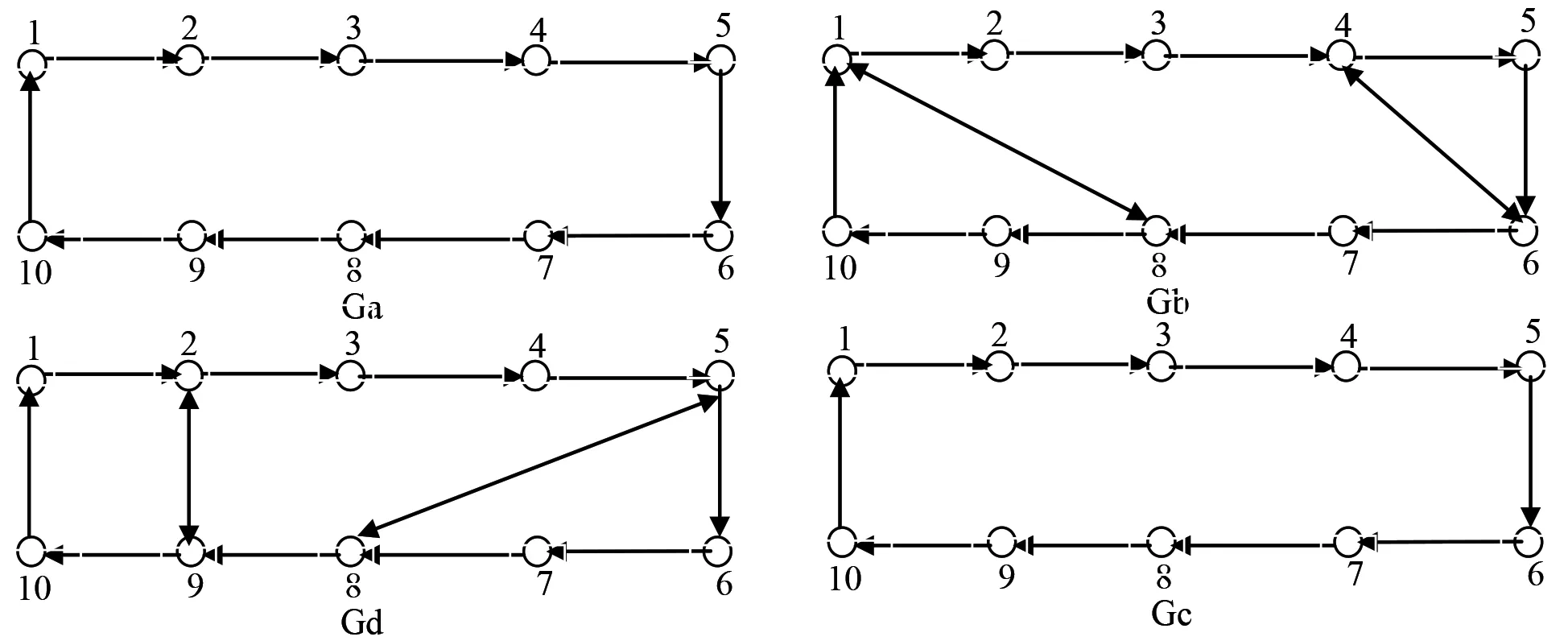
圖1 四個強連通平衡圖的例子
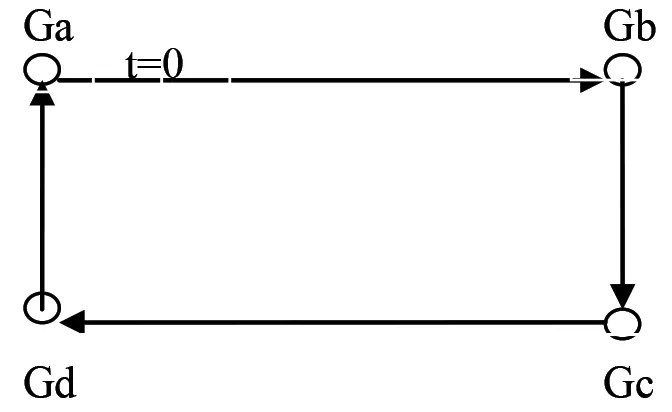
圖2 具有時變時滯的切換拓撲示意圖
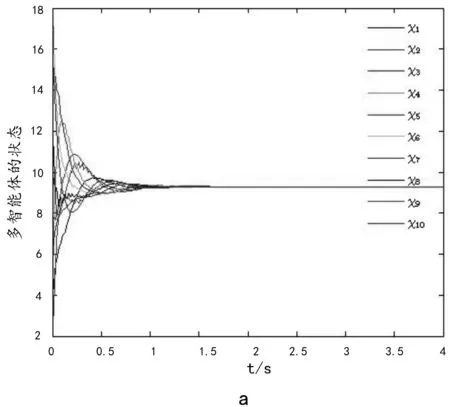
4 結論
本文討論了有向時變時滯多智能體網絡的加權平均一致性問題。采用狀態分解方法對系統進行轉化,利用LMI給出多智能體網絡取得加權平均一致性的充分條件。最后通過例子和仿真驗證了理論結果的正確性。
本文創新點:基于加權平均一致性,在有向切換拓撲和時變時滯多智能體網絡中,提出了一種新的控制協議,提高了控制系統的適應性和靈活性;運用正交變換把系統變為降維的等價系統;利用LMI的處理方法給出了系統取得漸進加權平均一致性收斂的充分條件。

