一種新的精英遺傳算法及在多彈攔截分配策略的應用*

王 儲 南 英 許 航

南京航空航天大學航天學院，南京 211100

0 引言

武器-目標分配問題(WTA)是多對多飛行器智能協同作戰中指揮決策的重要問題，其求解方法主要有枚舉法、分支界定法等精確算法[1]和遺傳算法，模擬退火算法，蟻群算法，粒子群算法等啟發式算法[2-6]。其中，遺傳算法(Genetic algorithm，GA)是一種有導向的隨機搜索算法，適合解決群體搜索最優化問題[7]，但其求解效率會隨著問題復雜程度逐漸降低，且容易陷入局部最優。一些學者為抑制其盲目尋優和過早收斂的局限性[8]，進行了很多研究。比如，Zhou等[9]將遺傳算法的均勻變異和交叉概念引入粒子群算法中，生成算法的更新方程。Wang等[10]將自適應遺傳算法與自適應變量鄰域搜索算法相結合，以平衡搜索和開發能力。Zhao等[11]引入自適應交叉與變異算子和模擬退火操作，抑制了算法早熟現象。王少蕾等[12]通過進化過程中變異、交叉因子的動態自適應策略，避免算法陷入局部最優。李瑞康等[13]將遺傳算法的交叉思想引入到粒子群更新的策略中，有效提升了算法的性能，擁有更好的綜合搜索能力。王光源等[14]根據種群多樣性測度動態調整粒子群算法的慣性權重，來抑制算法陷入局部最優。參考上述方法可知，引入自適應策略，一定程度上可以抑制算法陷入局部最優，但算法的收斂速度仍需改善，且合理地將遺傳算法與其他算法或策略融合可以改善算法的性能，但單一種群進化的多樣性遠不如多個種群協同進化好。因此，為了進一步提升算法的性能，快速收斂得到更好的最優解，還需擴大種群的多樣性，增強算法的搜索能力。

針對空戰戰場中多導彈對多目標的攔截-突防目標分配問題，本文采用一種基于自適應策略的改進多種群精英遺傳算法，即多種群自適應遺傳算法(MAGA)，來抑制算法過早收斂的情況，加快收斂速度尋找最優解。該算法在遺傳算法的基礎上，增加種群群落數量，引入自適應策略和遷移算子，采用精英選擇與備份策略，迭代計算得出最優解。選用3種算法與本算法進行對比，并通過數值仿真算例，驗證本文算法的有效性。

1 多彈攔截目標分配問題的數學描述

1.1 問題的數學描述

本文的研究背景為空中敵方多無人機來襲，我方發射多枚空空導彈進行攔截，導彈發射前將進行快速目標分配。本文導彈與目標均設為質點，且不考慮他們的空氣動力、環境影響等。

假定攔截導彈表示為Mi(i=1,2,…,m)，目標無人機表示為Nj(j=1,2,…,n)。每枚導彈對目標的擊毀概率已知，設導彈Mi對目標無人機Nj的擊毀概率矩陣為(pij)m×n。目標第j個無人機的威脅系數為wj，目標的威脅系數越大，則被分配的導彈數量越多。導彈攻擊目標的武器-目標分配決策矩陣為：

(1)

式中：vij∈Z(i=1,2,…,m;j=1,2,…,n)為第i個導彈分配給第j個目標無人機的火力單元數[12]。若vij=1，則表示導彈Mi攻擊目標Nj；若vij=0，則表示導彈Mi不攻擊目標Nj。

1.2 綜合優勢函數的構造

綜合優勢函數是一項用來評估目標分配結果好壞的重要指標。本文主要考慮2部分因素：1)考慮導彈攻擊目標的擊毀概率最大，即所有導彈毀傷目標的期望最大，可建立優勢函數f1，見式(2)。2)考慮導彈與目標在作戰中彈目的相對角度、相對速度與相對距離的限制與影響，參考文獻[15]，本文建立優勢函數f2，見式(3)。建立總的綜合優勢函數F=max(f1+f2)，見式(4)：

(2)

f2=c1sγsR+c2sγsv

(3)

(4)

1.3 約束條件

在多導彈攔截作戰的目標分配問題中，為盡可能還原真實作戰場景，增加了一些約束條件：

1) 進行目標分配時，每個目標都必須在其對應的攔截導彈的可攔截范圍內。

2) 當彈目距離小于或等于50m時，就認為目標無人機將被導彈擊毀。

Rm={R≤50}

(5)

3) 為盡最大能力攔截目標，每個目標必須被分配導彈。

(6)

式中：s表示某目標無人機最多允許分配的火力單元數。本文根據目標的威脅系數wj分配對應的導彈數量。

4) 模擬真實作戰中的資源分配不平等，導彈的數量一般應多于或等于目標數量。

(7)

根據以上建立的多導彈對多目標攔截的目標分配數學模型及約束條件，將其運用至下一節設計的算法中。

2 多種群自適應遺傳算法設計

MAGA曾被用于解決電網配電系統重構、TSP問題等。本文將其應用于空戰戰場中多導彈對多目標攔截對抗的目標分配問題。圖1為MAGA的框架圖。

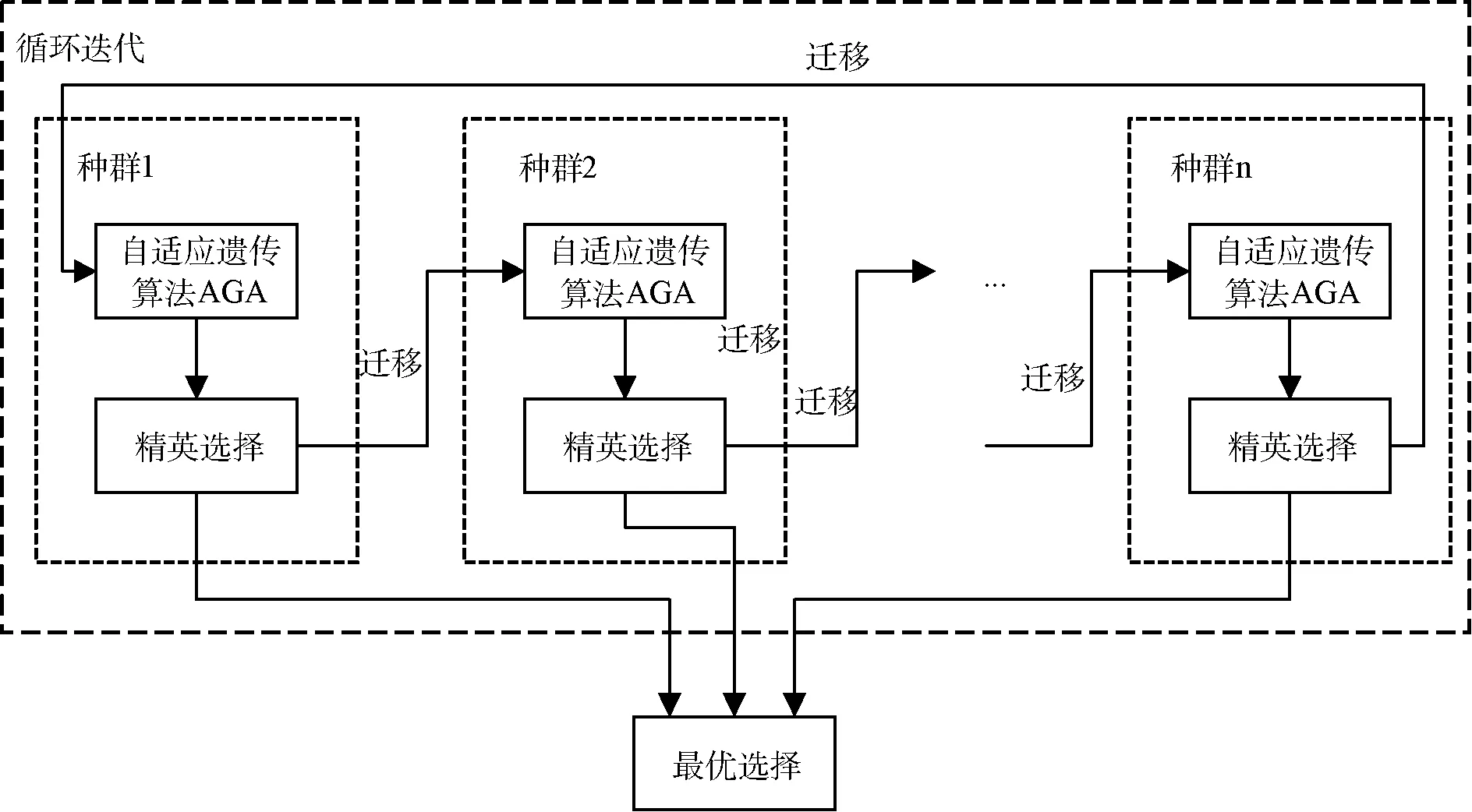
圖1 多種群自適應遺傳算法框架圖

本算法建立多個群落種群協同進化，擴大種群多樣性。每個種群均采用自適應策略動態改變交叉、變異概率，保留優秀個體，抑制算法早收斂。引入遷移算子，增加多種群間的聯系，設定精英選擇算子進行選擇與備份。該算法能有效抑制局部最優，加快收斂速度，獲得更優的分配結果。下面將在2.1～2.6節中詳細介紹本算法各環節算子的設計，并在2.7節中給出算法的詳細步驟。

2.1 基因編碼設計

初始種群PoPi(i=1,2,…,n)內的每條染色體個體編碼均代表目標分配的一個可行解。本文選用十進制整數編碼形式，根據目標的威脅度值，隨機生成初始種群，并保證個體編碼序列內無遺漏。導彈編號M從左到右依次遞增，染色體內編碼信息為目標無人機編號N，導彈與目標一一對應。以我方發射10枚導彈攔截敵方10架無人機為例，染色體編碼形式如圖2所示。

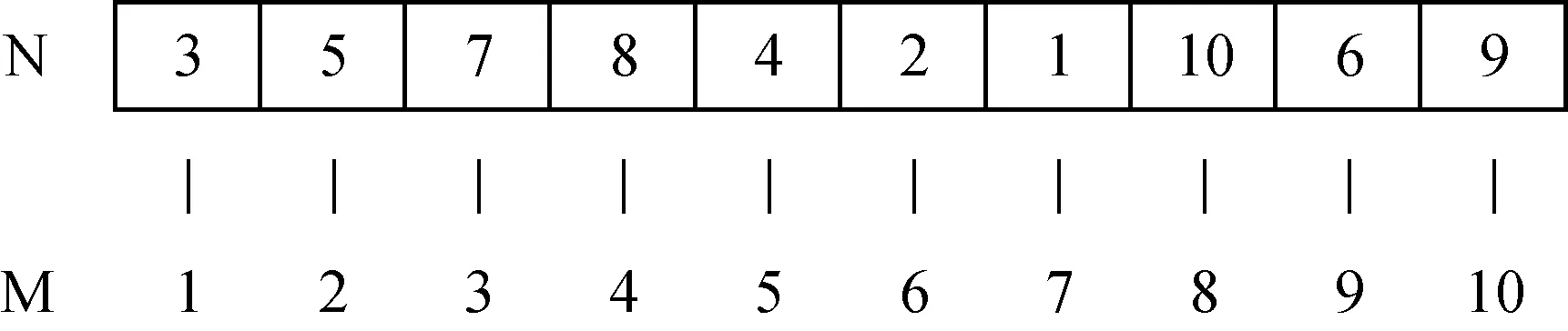
圖2 十進制整數編碼形式

2.2 適應度函數

適應度函數是用來評估個體是否達到最優的重要指標。本文的適應度函數主要考慮目標損毀率、角度、速度和距離等因素，選用1.2節中提出的綜合優勢函數F定義，見式(4)。根據式(4)計算每條染色體個體的適應度函數值，適應度值越大的個體，分配效果整體越優。

2.3 遺傳算子

遺傳算子主要包括選擇算子、交叉算子與變異算子。選擇算子能有效提升算法的收斂速度，交叉、變異算子能擴大種群多樣性，防止算法過早收斂。

1)選擇算子。采用輪盤賭法選擇優良個體，根據式(8)計算每個個體在子代中被選中的概率，并按照此概率選擇個體，構成子代種群進行下一步迭代。適應度值越大的個體被選中的概率越大。

(8)

2)交叉算子。核心思想是：在一個父代染色體P1中隨機選擇幾個位置，并在另一個父代染色體個體P2上找到相同信息的位置。分別將兩個父代染色體被選中的基因按照順序，互相填入對方的基因序列中，一次生成兩個子代染色體個體C1和C2。算法示意圖如圖3。

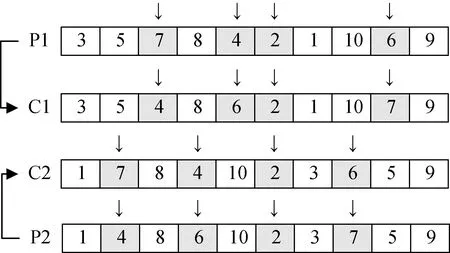
圖3 交叉算子示意圖

3)變異算子。采用交換變異的方式，每條染色體隨機選擇2個位置，互相交換編碼信息。在父代染色體P1內隨機選擇2個位置進行交換，產生子代染色體C1。算法示意圖如圖4。

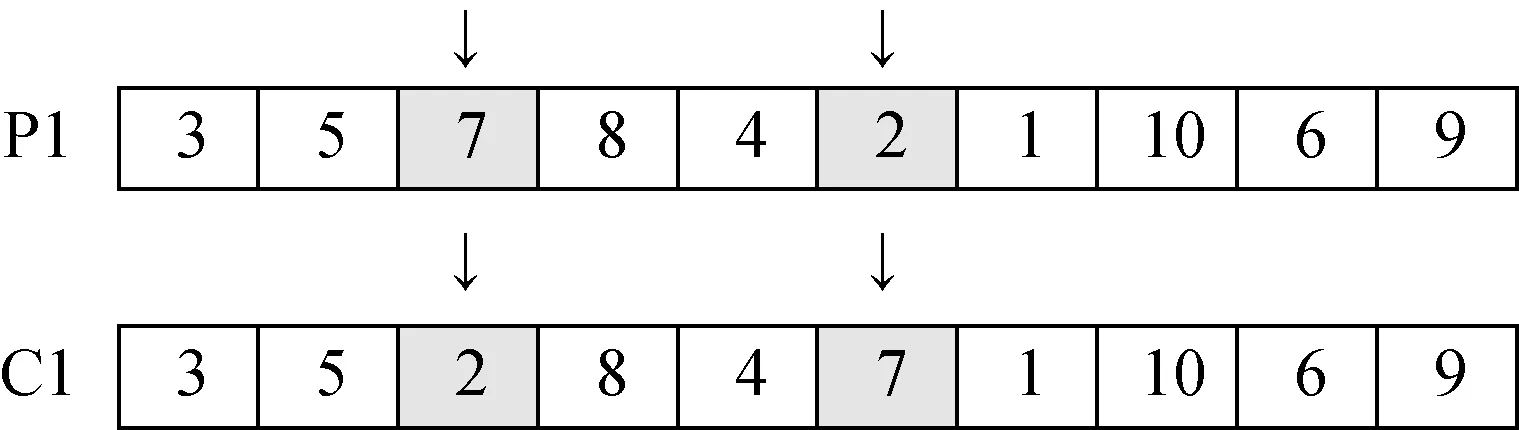
圖4 變異算子示意圖

2.4 自適應策略

交叉變異概率固定不變，存在優秀個體流失的風險。本文根據適應度函數的值自適應地改變交叉概率與變異概率，可以有效增加收斂速度，加速保留優良個體，淘汰低劣個體。本文設計的自適應交叉變異概率函數，見式(9)。

(9)

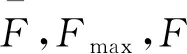
計算當前種群內個體的適應度函數值F，如果當前適應度值大于或等于平均適應度值，則通過式(9)計算交叉、變異概率；如果當前適應度值小于平均適應度值，則仍保持原來的交叉、變異概率進行遺傳操作。

2.5 遷移算子

遷移算子的主要作用是增加多群落之間的聯系，促進種群協同進化。本文將第1個種群PoP1適應度值排名前10的個體賦值給初始遷移種群MPoP。根據圖1的流程順序，每次迭代都將遷移種群MPoP與n個種群PoPi(i=2,3,…,n)依次互相更新進化，用適應度函數值靠前的前10個個體更新遷移種群MPoP′，同時按照種群容量擇優更新當前種群PoP′。

2.6 精英選擇算子

精英選擇策略是選擇種群中一部分優秀個體，組成一個精英種群保存備份，以防止精英個體在自適應交叉變異操作中流失。精英種群中的全部個體不參與交叉變異等遺傳操作。

分別將種群PoPi(i=1,2,…,n)的前k個優秀個體保存于各自的精英種群GPoPi(i=1,2,…,n)中，并隨著每次循環迭代，保證每個精英種群中始終保存各自種群發展過程中的前k個優秀個體。

2.7 MAGA算法描述

采用MAGA解決多導彈對多目標攔截對抗的目標分配問題，具體算法流程框圖見圖5，算法步驟如下：

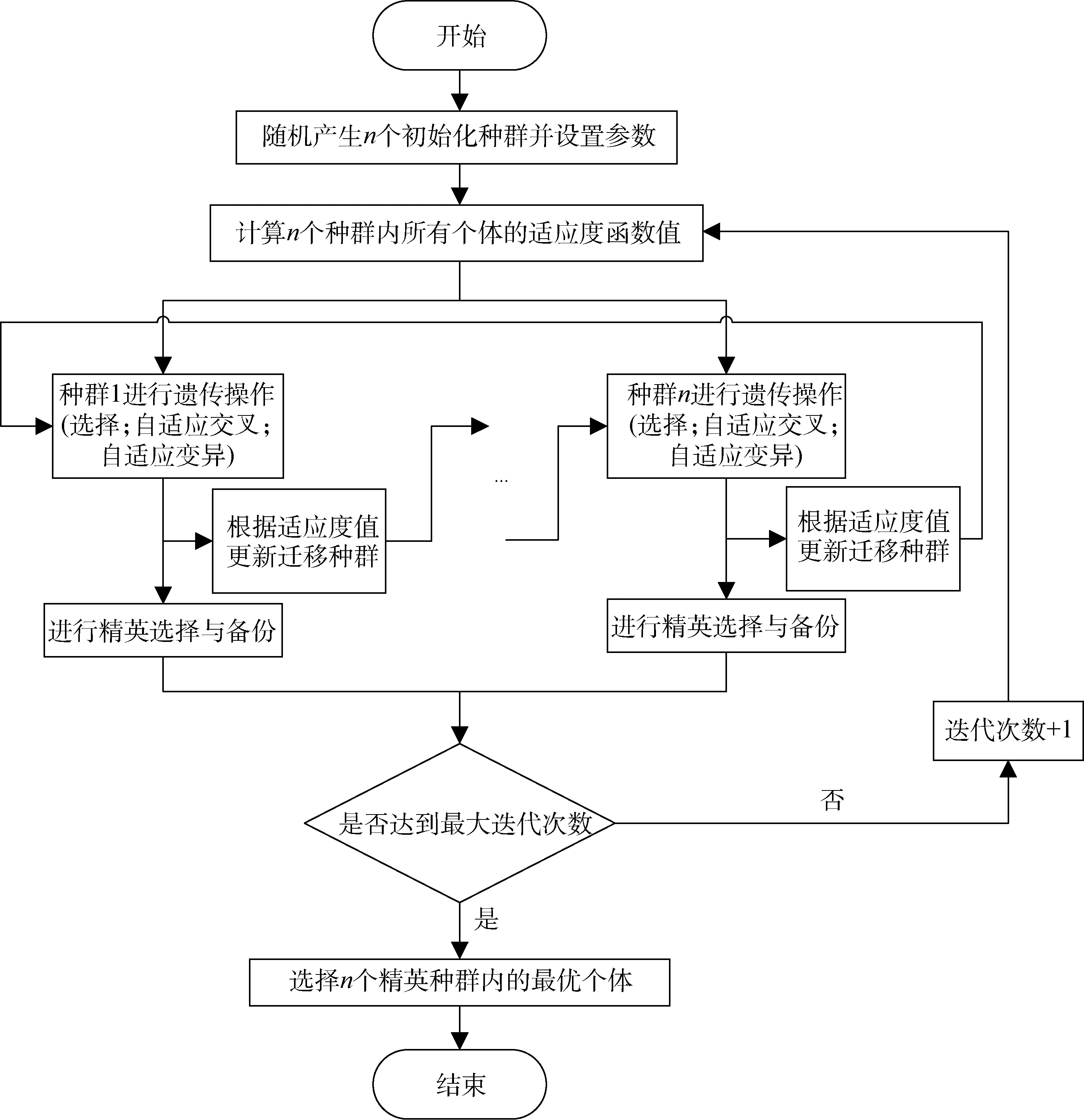
圖5 多種群自適應遺傳算法流程框圖

1)種群初始化。設定種群數目x，每個種群內含有個體數目y，隨機產生共x×y條染色體。導彈數目M，目標無人機數目N。設定循環迭代次數t，最大交叉概率Pc1，最小交叉概率Pc2，最大變異概率Pm1，最小變異概率Pm2。

2)計算適應度值。解碼種群內每條染色體個體，得到武器-目標分配決策矩陣V，根據式(4)計算每條染色體個體的種群適應度值。

3)遺傳操作。根據式(8)進行輪盤賭選擇操作。根據式(9)計算每條染色體個體的自適應交叉與變異概率，進行交叉、變異操作，得到每個種群內的新子代種群。

4)遷移操作。對每個種群內的個體按照適應度值大小進行排序，選擇更新每個種群的遷移種群MPoP與當前子種群。

5)精英選擇與備份。按照精英選擇策略，對每個種群進行精英選擇與備份操作，每次迭代都將更新精英種群。

6)判斷。判斷是否達到最大迭代次數t，若是，則進行7)；若否，則轉2)循環迭代。

7)最優選擇。將n個種群中的精英種群，根據適應度值進行逐一比較，得出最優染色體個體，即多對多攔截對抗的目標分配問題的最優解。算法結束運行。

3 數值仿真與分析

以多導彈對多目標的攔截對抗目標分配問題為背景，通過數值仿真分析，驗證算法性能。假定我方共有5個火力平臺，每個火力平臺可發射3枚導彈，導彈總數目M=15，導彈均采用三維比例導引法來攔截目標。敵方目標無人機分3組進攻，目標總數目N=10，目標分別做不同類型的sin型機動。假設導彈的類型各不相同，每枚導彈都對特定目標有高毀傷概率，如0.7～0.9，對其他目標的毀傷概率為0.5，毀傷概率值設定見表1。本文根據目標的威脅值分配相應數量的導彈攔截，假定目標的威脅值為wj=[1,2,1,3,1,2,1,1,2,1]。

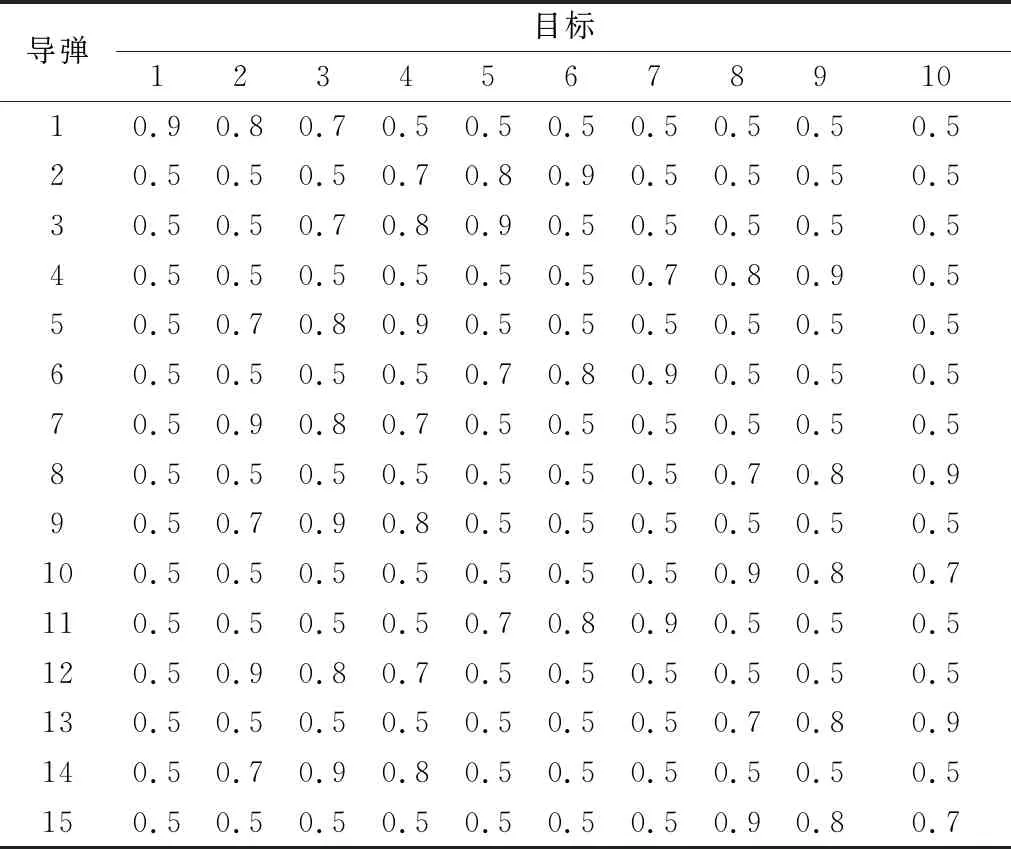
表1 導彈對目標的攻擊毀傷概率表

其他參數設定為：種群數目x=3，每個種群內含有個體數目y=30，循環迭代次數t=500，隨機產生最大交叉概率Pc1=0.8+rand(0,0.1)，最小交叉概率Pc2=0.7，隨機產生最大變異概率Pm1=0.1+rand(0,0.1)，最小變異概率Pm2=0.05，適應度函數常數c1=0.5,c2=0.5。rand(0,0.1)表示在(0,0.1)區間均勻分布的隨機數。

應用MAGA進行武器-目標分配，為驗證本文設計算法的有效性，選用遺傳算法(GA)，自適應遺傳算法(AGA)，多種群遺傳算法(MGA)進行對比分析。通過20組數值仿真驗證，可得到MAGA算法的最優目標分配方案為：[1,6,5,9,4,7,2,10,3,4,6,2,9,4,8]，最優適應度為15.713。四種算法的最優適應度平均值與最大值，見表2。

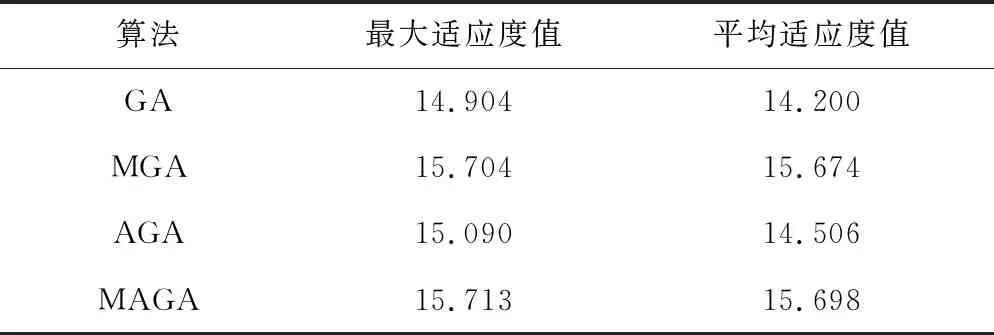
表2 四種算法的最優適應度值

基于MAGA算法導彈攔截目標的軌跡，見圖6～7。可見本算法可以對機動目標很好地進行分配，且當目標威脅度大于1時，可分配多個導彈進行攔截。四種算法的最佳適應度變化曲線和最優適應度函數箱型圖，見圖8～9。

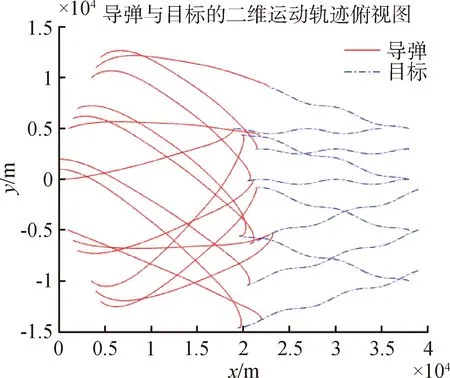
圖6 基于MAGA算法的多對多攔截軌跡俯視圖

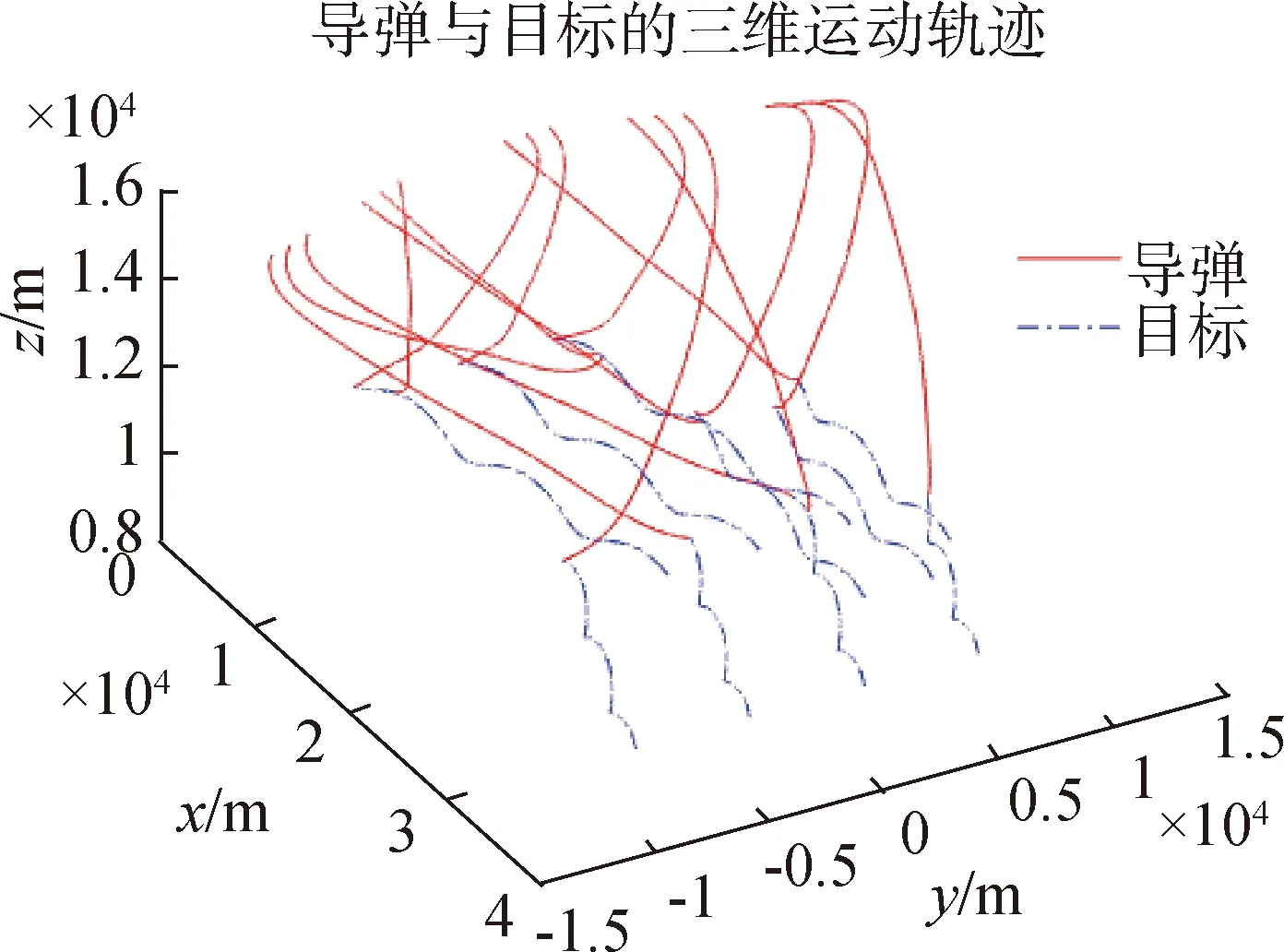
圖7 基于MAGA算法的多對多攔截三維軌跡圖

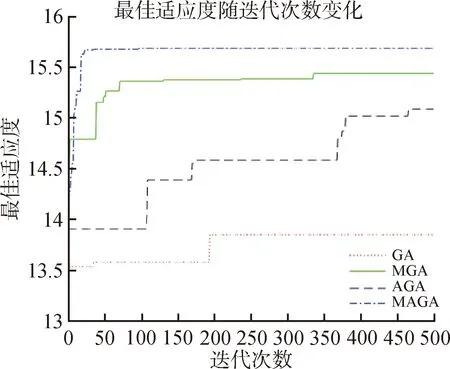
圖8 四種算法的適應度對比

分析圖8的仿真結果，對比曲線GA與MGA可知，MGA尋找的最優解遠優于GA尋找的最優解，單種群遺傳算法容易陷入局部最優，多種群遺傳算法能有效地擴大種群多樣性，抑制算法早熟；對比曲線MGA與MAGA可知，MAGA的收斂速度優于MGA，MAGA約在迭代20步左右收斂到較優解，MGA則約在80步左右收斂到較優解。可見引入自適應策略，可以有效增加算法的收斂速度，還可以抑制算法局部最優。

由圖9的箱形圖和表2可知，MGA與MAGA的平均適應度值很高且變化幅度很小，但MGA存在一些離散點，穩定性略差于MAGA；GA與AGA相比可知，AGA整體優于GA，可見加入自適應策略還可以獲得更好的最優解。

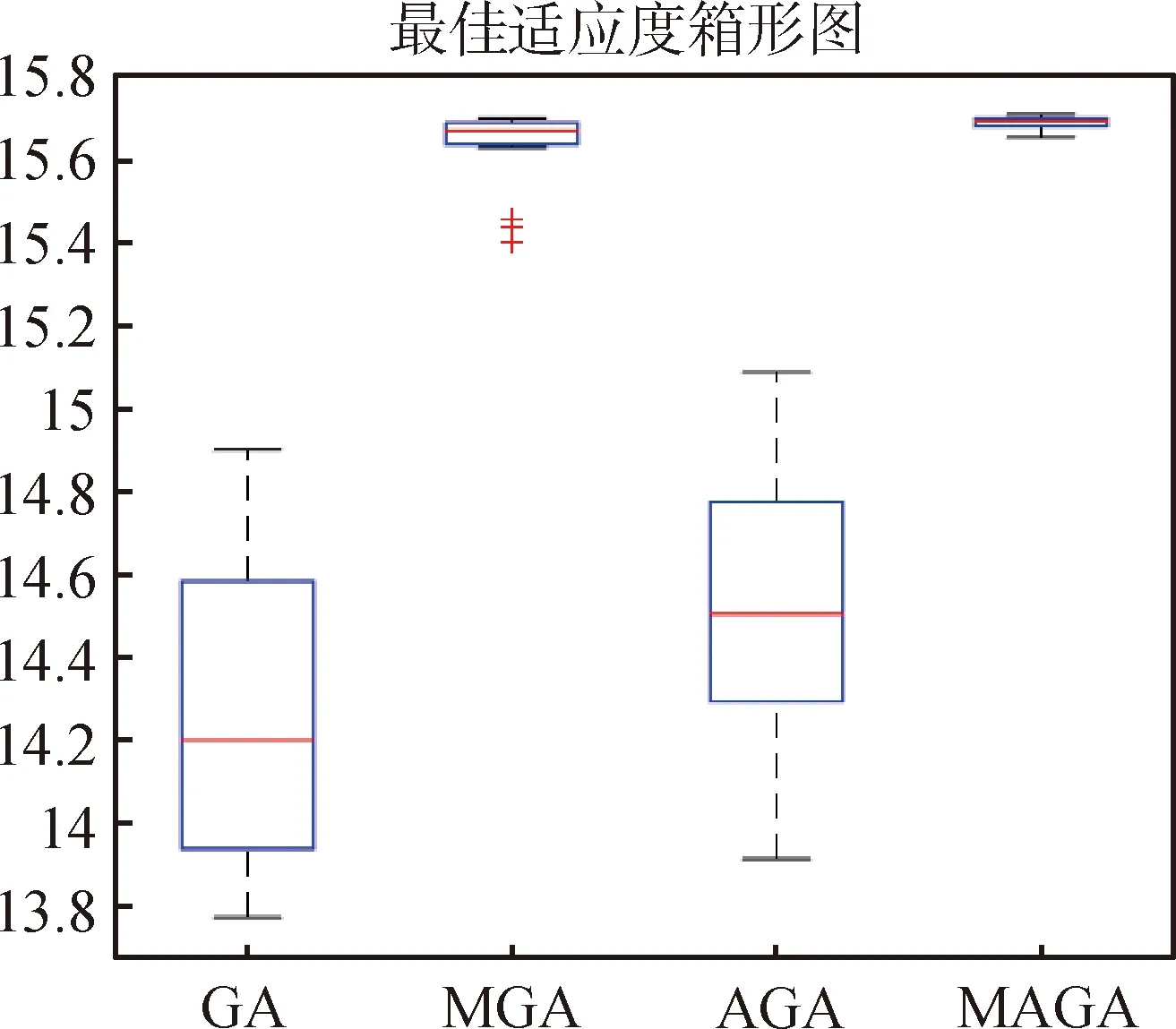
圖9 四種算法的最優適應度箱形圖

4 結束語

本文在多導彈對多目標的攔截對抗目標分配問題的實戰背景下，提出將多種群自適應遺傳算法(MAGA)應用于武器-目標分配問題中，總結如下：

1)適應度函數與約束條件。本文選用武器擊毀目標概率最大為評估標準，增加導彈與目標的相對距離、速度和角度等變量，使得問題描述地更精確真實，求解精度得到提高。

2)多個種群與遷移算子。本文采用多個種群做并行迭代計算，通過遷移算子加強種群間的聯系，有效擴大種群多樣性，抑制算法過早收斂。

3)自適應策略與精英選擇策略。本文引入自適應策略動態改變交叉、變異概率，有效保留優秀個體，加速淘汰低劣個體。引入精英選擇策略來選擇備份優秀個體。

通過與GA、MGA、AGA算法進行對比分析，驗證了本文設計的MAGA算法能有效提高求解精度與收斂速度，抑制局部最優。在多導彈攔截多機動目標的算例中，證明了該算法可用于解決一定規模空戰中的武器-分配問題，對多導彈攔截多目標作戰的智能決策有一定的參考價值。