改進PSO優化WNN的液體火箭發動機故障檢測*

許 亮 馬 碩 薛 薇 李寧寧

1.天津理工大學電氣電子工程學院，天津市復雜系統控制理論及應用重點實驗室，天津 300384

2.北京航天動力研究所，北京100076

0 引言

液體火箭發動機的故障檢測對于提高發動機運行的準確度具有十分重要的意義。隨著現代航天技術的飛速發展，液體火箭被越來越多的國家發射使用[1]。液體火箭的動力裝置系統主要由推進劑輸送和增壓系統及液體火箭發動機兩大部分組成。液體火箭發動機的故障檢測顯得尤為重要[2-5]。

經常采用神經網絡算法預測發動機故障檢測的問題。眾所周知，神經網絡具有較高的非線性映射能力以及高效的自主學習性和容錯能力[6-8]，因此神經網絡成為液體火箭發動機故障檢測的重要手段[9]。通常，人們都使用BP神經網絡進行運算，但BP神經網絡結構設計上具有盲目性的缺點。最近，越來越多的人通過使用小波神經網絡進行預測[10-11]，相比于前向的神經網絡，小波神經網絡具有更強的學習能力，精度也更高，它的基元和整個結構是依據小波分析理論確定的，所以結構更加簡單，收斂速度更快。

智能算法在實際應用中會根據具體問題進行改進[12]。劉利軍、雷宇等提出了一種雙向長短時記憶神經網絡的航空發動機氣路部件故障診斷模型，實驗結果充分表明雙向LSTM模型的優越性[9]。胡昌華、張軍波等提出一種基于小波和人工神經網絡的方法實現對系統故障檢測與診斷的研究[13]。何浩、胡小平等采用支持向量機SVM檢測和診斷液體火箭發動機故障診斷的數據，結果證實了該方法的正確性和可行性[14]。董周杰、郭迎清提出一種基于數據驅動的綜合模糊聚類算法用于液體火箭發動機的故障診斷[15]，模型仿真結果表明該故障診斷算法能夠準確及時地檢測并隔離出故障。劉明、楊明等提出基于粒子群算法求解單顆衛星軌道參數、解析法求解星座軌道參數的方法。仿真表明，該方法具有較好的工程應用價值[16]。王娟、吳憲祥和郭寶龍提出一種結合Ferguson樣條路徑描述和改進粒子群優化算法的路徑規劃方法[17]，將其用于移動機器人的路徑規劃，證實有一定的實用價值。

曾勇、張金奮等人在船舶避碰決策案例上為了避免陷入局部最優，提高全局搜索能力，讓粒子群算法與遺傳算法相結合，提高收斂精度，加速全局尋優[18]。戴航、王春波等人針對優化電池損耗及儲能系統收益情況提出一種雙適應度混沌粒子群算法，引入混沌擾動，解決了粒子群算法全局尋優能力不足，罰函數難以選取等問題[19]。基于此，為了解決傳統粒子群算法初期容易陷入局部最優的問題，并且為了提高運算效率[20-21]，本文采用逐漸遞減的選取方式，將粒子群優化算法的慣性權重和學習因子進行改進，并與小波神經網絡相結合，提出一種改進的粒子群算法(PSO)與小波神經網絡(WNN)相結合的方法，將其用于液體火箭發動機的故障檢測中。

1 PSO-WNN優化模型

1.1 小波神經網絡算法

為了能根據液體火箭發動機的性能參數判斷出發動機是否發生故障，本文利用小波神經網絡參與建立對其進行預測的神經網絡模型。張清華等人于1992年首次提出了小波神經網絡(wavelet neural network，WNN)，并在函數學習上取得了成功[6]。小波神經網絡是小波變換和人工神經網絡的結合。小波神經網絡是基于BP神經網絡拓撲結構的神經網絡，其中小波基函數用作隱含層節點的傳遞函數，信號向前傳播而誤差向后傳播。小波神經網絡集人工神經網絡和小波分析優點于一身，不僅網絡收斂速度快，又能避免陷入局部最優，同時又有時頻局部分析的特點[13,22-23]。小波神經網絡的拓撲結構如圖1所示。

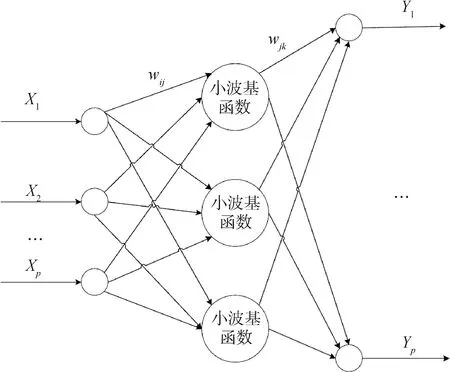
圖1 小波神經網絡拓撲結構

在圖1中，X1,X2,…，Xp是小波神經網絡的輸入參數，Y1,Y2…，Yq是小波神經網絡的預測輸出，ωij和ωjk為小波神經網絡權值。

在輸入信號序列為xi(i=1,2,…,p)時，隱含層輸出計算公式為：

(1)

式中，h(j)為隱含層第j個節點的輸出值；bj為小波基函數hj的平移因子；aj為小波基函數hj的伸縮因子；ωij是輸入層和隱含層的連接權值；hj為小波基函數。

本次液體火箭發動機故障檢測仿真實驗將Morlet母小波基函數作為小波基函數，其數學公式為：

(2)

小波神經網絡輸出層計算公式為：

(3)

式中，l隱含層節點數；ωjk為隱含層到輸出層權值；h(i)為第i個隱含層節點的輸出；m為輸出層節點數。

小波神經網絡權值參數校正算法與BP神經網絡權值校正的算法基本類似，網絡的權值和小波基函數參數采用梯度修正法進行修正，通過大量數據的訓練，使小波神經網絡的真實輸出與期望輸出之間誤差最小。

小波基函數的系數和小波神經網絡的權值通過預測誤差e校正，公式如下：

(4)

(5)

(6)

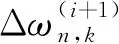
(7)

(8)

(9)

式中，η為學習速率。

由于本案例中的小波神經網絡的權值和小波基函數的參數采用的修正方法為梯度學習算法，此算法也有一定缺點，比如在靠近極小值時容易造成進化緩慢并且容易陷入最小，所以為了提高神經網絡學習速率，本文采用增加動量項的方法，增加動量項的權值和小波基函數參數修正公式為：

(10)

(11)

(12)

式中，k為動量項學習速率。

1.2 粒子群算法

粒子群優化算法(PSO)最初起源于對鳥群捕食行為的觀察和研究[16,24]，此算法中每一個由擬合函數確定的每個擬合值都有一個對應的粒子對應關系。粒子的速度不僅決定了粒子的行進方向，還指示了粒子在空間中行進的距離。每個粒子可以通過自身以及其他粒子的運動經驗動態調整其自身速度，實現個體在可解空間中的尋優[25]。

個體極值由Pbest表示，指的是個體粒子由所遍歷位置中各個粒子計算得出的擬合值的最佳位置；群體極值由Gbest表示，是指種群中所有粒子搜索到的適應度的最優位置。粒子每次移動搜索后，適應度值都會隨著位置的變化而重新計算，并通過比較新粒子的適應度值與個體極值和群體極值的適應度值來更新Pbest和Gbest的位置。

每個粒子更新速度和位置的數學公式如下所示：

(13)

(14)

式中，ω為慣性權重；d=1,2,…,n；k為當前迭代次數；Vid為粒子的速度；C1和C2為非負的常數，稱為加速度因子；r1和r2為分布于[0,1]之間的隨機數。一般建議將其位置和速度限制在一定的區間[26][-Xmax,Xmax][-Vmax,Vmax]，以防止粒子的盲目搜索。此方法稱之為BPSO。

2 基于IPSO-WNN模型建立

2.1 粒子群算法的改進

建立模型初期的時候，由于空間很大，導致粒子群的搜索范圍很大，為了避免粒子過早陷入局部最優，同時提高迭代后期的局部搜索能力，并隨著迭代次數的增加加快系統的收斂速度，所以將慣性權重和學習因子的選取采用逐漸遞減的方式，其動態調整過程如下：

(15)

(16)

式中，ω是慣性權重，ωmax是慣性權重最大值，ωmin是慣性權重最小值，k是當前迭代次數，是變量，kmax是總共迭代次數，是常量。由上述公式可以看出，慣性權重和迭代次數成負相關，并且慣性權重是迭代次數的二次函數。

改進之后的粒子群算法，迭代初期的時候，ω變化緩慢，有利于在初始迭代時尋找滿足條件的局部最優值，在接近最大迭代次數時，ω變化較快，在尋找到局部最優值之后能夠快速地收斂逼近于全局最優值，提高運算效率。此改進的粒子群算法稱之為IPSO。

2.2 IPSO-WNN的參數尋優流程如下

1)確定小波神經網絡的拓撲結構，確定WNN的輸入層、隱含層、輸出層的節點數目，確定迭代次數maxgen、種群規模sizepop、個體和速度最大最小值、參數學習率；

2)進行WNN的權值初始化和節點初始化；

3)產生初始粒子和速度，計算各個粒子適應度函數值，比較所有粒子的適應度值，從中選取最好的粒子作為Pid,選取粒子歷史最優狀態為個體最優[27]Pgd；

4)根據公式(13)和(14)更新粒子的速度和位置；

5)根據適應度函數重新計算每個粒子的適應度，并更新粒子最優值[27]Pid和Pgd；

6)進行條件判斷：若迭代次數小于設定的最大值或誤差參數小于設定的誤差值，則得到最優粒子即WNN參數；否則，跳轉到步驟3)[27]；

7)確定WNN的最優網絡參數，輸入訓練參數并進行WNN模型的預測[27]。

IPSO-WNN流程圖如圖2所示。

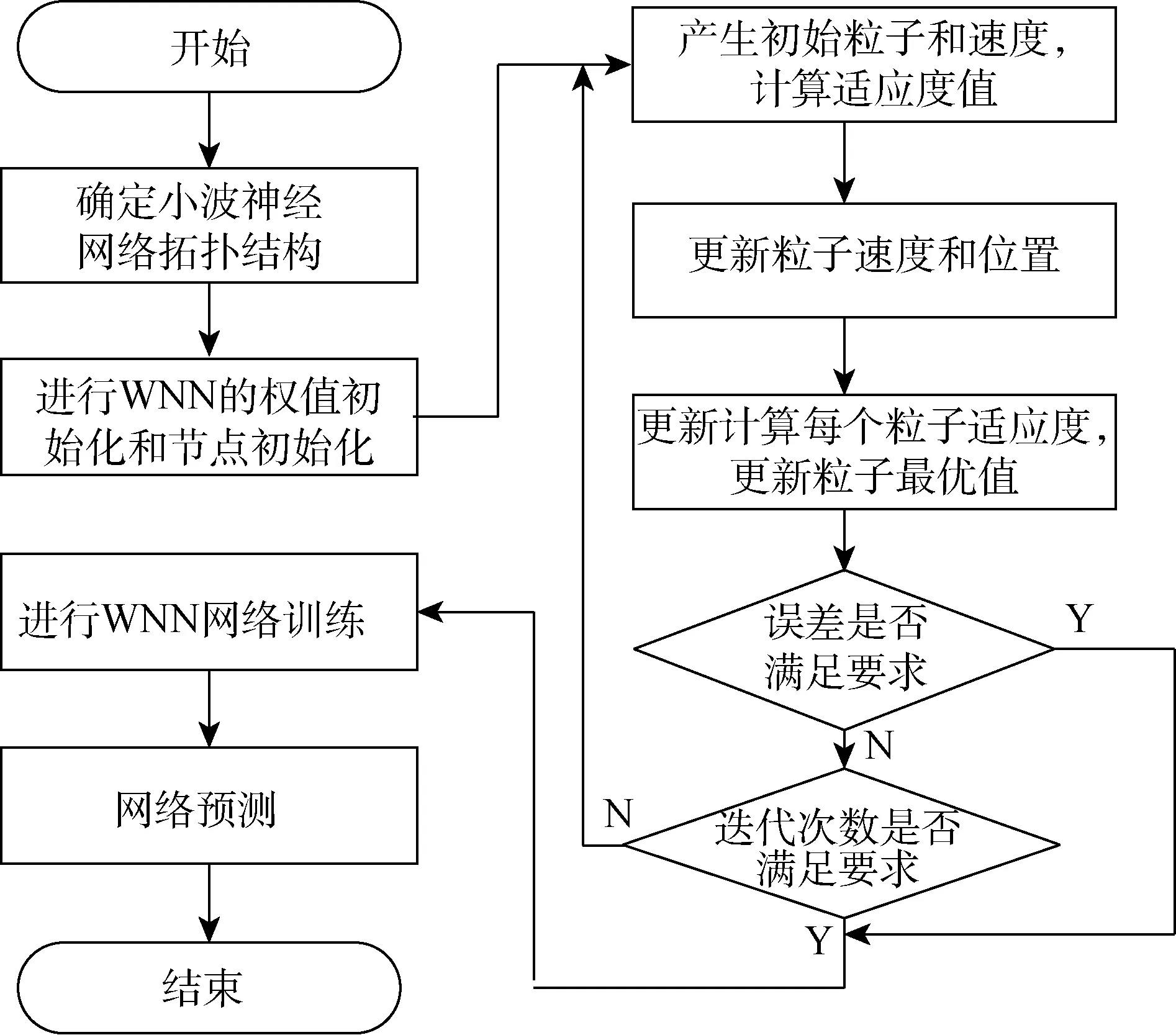
圖2 IPSO-WNN流程圖

3 IPSO-WNN在液體火箭發動機故障檢測中的仿真校驗

3.1 訓練樣本的選取

本次實驗選取某一型號的液體火箭發動機試車數據進行實驗和仿真，采用MATLAB_R2016a軟件進行仿真，隨機選取232組數據進行實驗，取正常數據和非正常數據各10組作為測試數據樣本，其余數據作為訓練樣本進行訓練。

粒子群算法參數設置如下：種群規模是20；隱形節點個數n=10；ωmax=0.9；ωmin=0.4；cmax=2.1；cmin=0.8；Vmax=1；Vmin=-1；學習概率lr1=0.01，lr2=0.001。

3.2 仿真結果對比

對改進粒子群優化小波神經網絡算法(IPSO-WNN)與未改進粒子群優化小波神經網絡算法(BPSO-WNN)以及單獨使用小波神經網絡算法(WNN)進行仿真計算比較，為了能直觀地看出比較結果，采用誤差圖對比和所用時間來評判故障預測模型的優劣。

本文在使用相同的訓練數據和測試數據的基礎上，將改進的粒子群優化小波神經網絡的故障檢測預測模型與傳統的粒子群優化小波神經網絡的故障檢測預測模型的實驗結果進行比較。預測值與實際輸出值的對比結果分別如圖3和圖4所示，其中橫坐標為數據樣本編號，縱坐標為輸出結果值。三者的誤差對比如圖5所示，其中橫坐標為粒子的迭代次數，縱坐標為誤差數值。

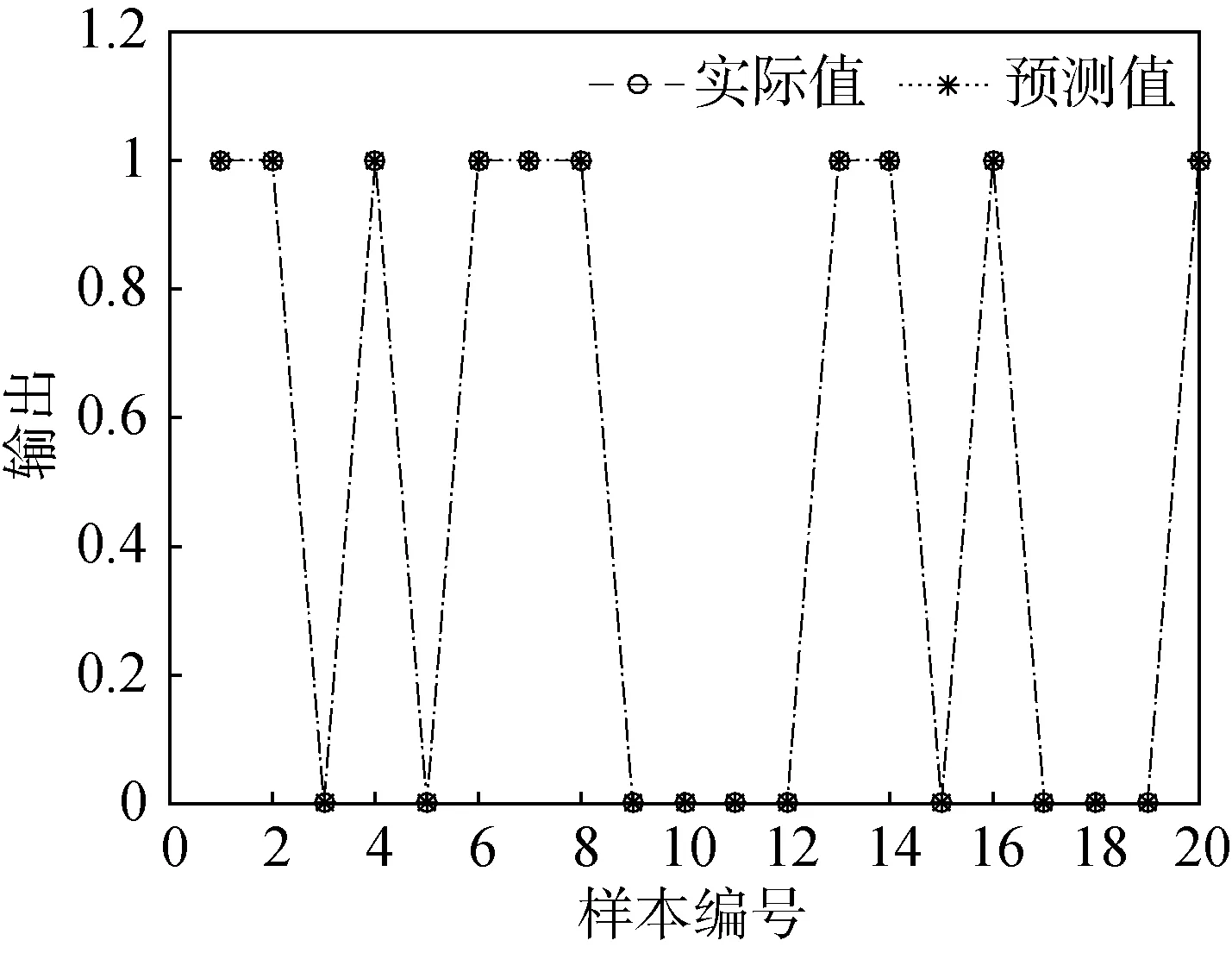
圖3 IPSO-WNN結果對比圖

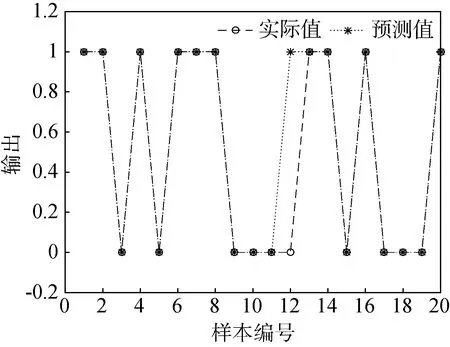
圖4 BPSO-WNN結果對比圖

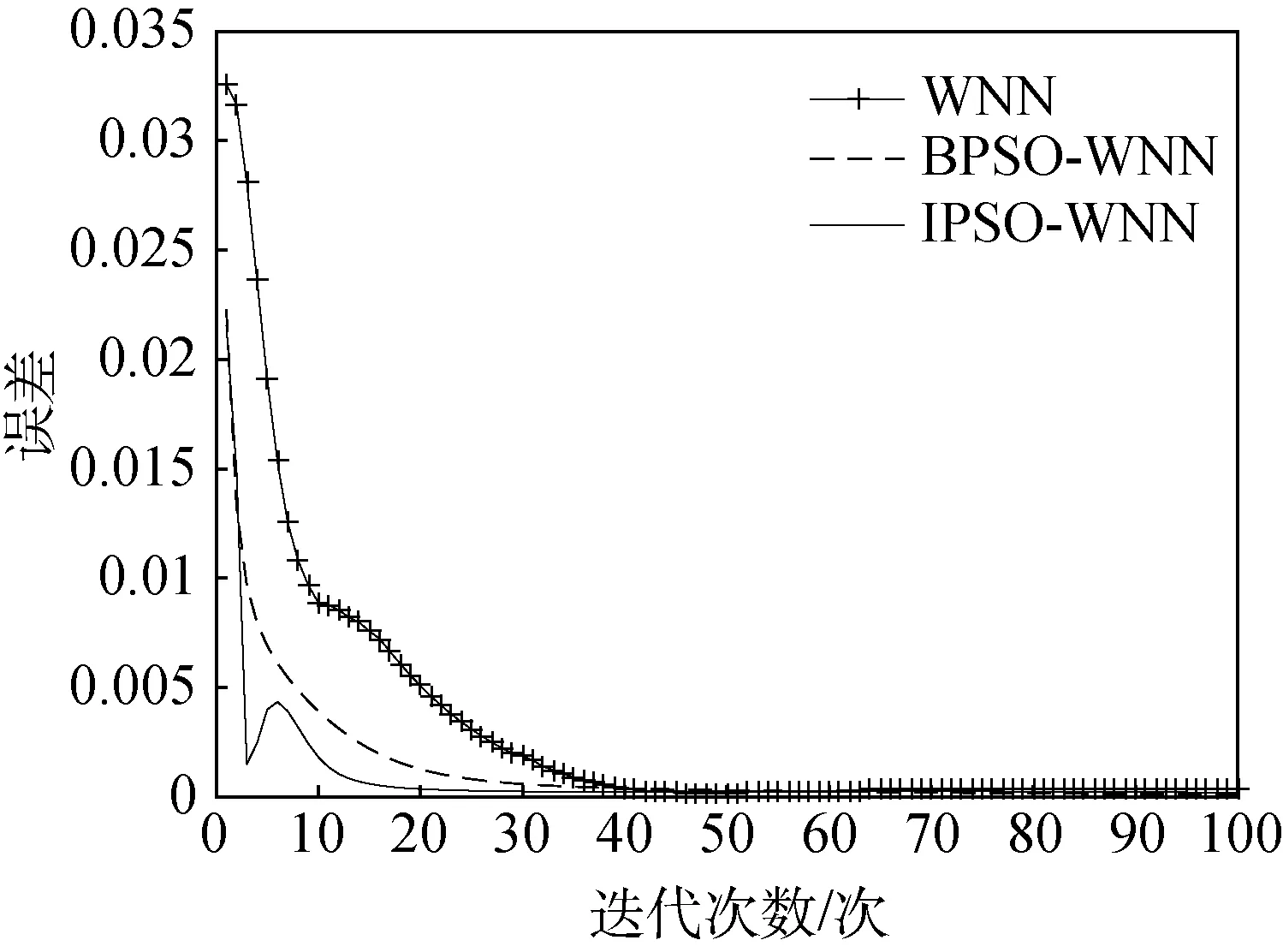
圖5 誤差圖

圖3為IPSO-WNN算法預測模型的輸出對比圖，圖4為BPSO-WNN算法預測模型的輸出對比圖。從圖的比較中可以看出，IPSO-WNN算法預測模型的預測值和實際值更加吻合，IPSO-WNN預測模型與液體火箭發動機實際情況更加切合，對應預測曲線的擬合效果明顯優于另一個模型，具有較強的預測能力。圖5中用“+”號標記的線為WNN算法預測模型的誤差圖，虛線為BPSO-WNN算法預測模型的誤差圖,實線為IPSO-WNN算法預測模型的誤差圖。從這3種直線的對比可以看出IPSO-WNN算法的迭代次數少于BPSO-WNN算法和WNN算法的迭代次數，IPSO-WNN算法比BPSO-WNN算法和WNN算法的誤差下降得更快，更快地達到最小值，并趨于穩定。從中可以得出雖然IPSO-WNN模型比BPSO-WNN模型和WNN算法所需要的迭代次數減少，但新算法能夠在迭代次數更少的前提下誤差降到最低并趨于穩定。

從表1可以看出3種模型結構所用時間的對比，分析可得，IPSO-WNN模型在3種結構中所用時間最少，說明優化后的此模型比其他2種擁有更好的精確度，實驗效果更加理想。

表1 三種模型運行時間對比

綜上3種故障檢測模型對比結果表明：基于WNN的故障檢測模型需要訓練的時間較長，準確率較低；基于BPSO-WNN的故障檢測模型雖然能夠通過PSO優化算法優化選擇基于WNN的故障檢測模型中的參數，但冗余數據增加了訓練的時間，相對于WNN提高了結果的準確性；基于IPSO-WNN的故障檢測模型，通過對傳統PSO的慣性權重和學習因子的選取，采用逐漸遞減方式加快收斂速度，避免過早陷入局部最優，在迭代后期加大局部搜索能力。從實驗結果中可以看出此方法相比于以上2種方法預測更加準確，速度更快，實驗結果更加理想。

4 結論

使用改進后的粒子群算法優化小波神經網絡(IPSO-WNN)，對液體火箭發動機進行故障檢測，結果表明：

1) 改進后的粒子群算法可以避免其過早陷入局部最優，提高迭代后期的局部搜索能力，并隨著迭代次數的增加加快收斂速度;

2) 粒子群優化算法可以與小波神經網絡算法相結合，結合后的新算法可以對液體火箭發動機進行有效的故障檢測;

3) 在本次液體火箭發動機的故障檢測預測實驗中，修正后的IPSO-WNN算法模型與WNN算法和BPSO-WNN算法相比，IPSO-WNN算法模型提高了故障檢測預測的精度。