人工智能元素融入大學數學課程的可行性探析

倪丹

【摘 要】 目前，人工智能相關的大學教育越來越受到重視。人工智能需要堅實的數學基礎。大學數學課程體系中的《微積分》《線性代數》《概率論與數理統計》三門課程，在理論和實踐上都與人工智能有著密切的聯系。本文列舉并分析了一些具體的數學知識及其在人工智能方面的應用，這些探討都展示了將人工智能元素滲透到大學數學課程中的可行性。

【關鍵詞】 人工智能;梯度;泰勒級數;線性變換;貝葉斯公式

【中圖分類號】 O1-4 【文獻標識碼】 A 【文章編號】 2096-4102（2021）05-0030-03

隨著人工智能的迅速發展，我國制定了相應的國家發展戰略，將人工智能的普及、推廣和基礎教育置于非常重要的位置。

大學本科階段的數學作為廣義高等數學教育的起點，其知識體系主要由《微積分》《線性代數》《概率論與數理統計》這三門課程構成。人工智能所需要的最基本的數學知識主要來自于這些課程。筆者認為，在這些數學課程中滲透人工智能思想，將對點燃學生對于人工智能學習興趣的火花大有裨益。以下就這三門課中一些與人工智能有密切關聯的知識進行舉例分析，希望對相關數學課程的教學改革起到拋磚引玉的作用。

一、人工智能與《微積分》

（一）梯度

人工智能的主要思想是尋找一種用于數據分類和預測的優化擬合函數。因此，優化理論在人工智能實踐中起著非常重要的作用。在一定約束條件下，找到目標函數的最優值就是我們所說的最優化。大學微積分課程中便有不少優化方面的內容。比如，在多元函數微分方法及其應用一章中，課本在介紹完方向導數之后引入了梯度。我們知道，梯度的方向是獲得方向導數的最大值的方向，梯度的值則是方向導數的最大值。為了獲得對梯度的清晰認識，我們可以追溯到介紹導數的含義和幾何背景的章節。

梯度可以看作是導數的多變量推廣。與標量值的導數不同，梯度是一個向量值函數，它表示函數圖切線的斜率。更精確地說，梯度的負方向是函數達到其局部最小值的最快方向。梯度下降法是人工智能實踐中常用的優化算法。它的核心思想是在當前位置找到梯度的最快下降方向，以便逐步逼近最優目標函數。

梯度則指明了從當前位置下降的最陡方向。以二元函數為例，目標函數J（w）將表示為J（w1，w2）。相應的三維圖形類似于一座山，谷底對應于J（w1，w2）的最小值，而坡度（梯度的反方向）則指出了下山最快的方向（見圖1）。

（二）泰勒級數

人工智能的強大之處是其算法的效率和準確性。當運用人工智能技術解決一個實際問題時，常常需要一個具體的數學模型。而許多問題的數學模型通常很復雜。這些復雜的問題往往難以解決甚至不可能精確地解決。這時，找到一個不那么精確但有效的解決方案可能是最好的選擇。而微積分中的泰勒公式的最大優點是它將一個復雜的函數近似為一系列冪函數的簡單線性疊加，從而便于比較、求導、求積分和求解微分方程等。這一優點使得泰勒級數成為研究神經網絡的有力工具。

“無窮級數”章節里，我們可以看到使用泰勒級數來逼近函數的神奇效果：以y=ex在x=0處的3階、7階泰勒展開為例，見圖2。

《微積分》是人類數學史上和人類思維領域最偉大的成果之一，而人工智能在某種意義上是對人類思維的模擬和進一步發展。從上面梯度和級數例子的展示，我們可以看到，學生在微積分課堂的學習中，已經可以直接追溯探討到人工智能主要思想的起點。

二、人工智能與《線性代數》

人工智能技術最終都是建立在與《線性代數》密不可分的數學模型之上的。特別是在處理多維數據時，需要用《線性代數》簡潔明了地描述問題，為分析和解決問題打下基礎。事實上，隨著機器視覺成為人工智能的重要組成部分，投影技術和映射技術越來越受到人們的重視。而投影和映射的基本原理便來自于線性代數。

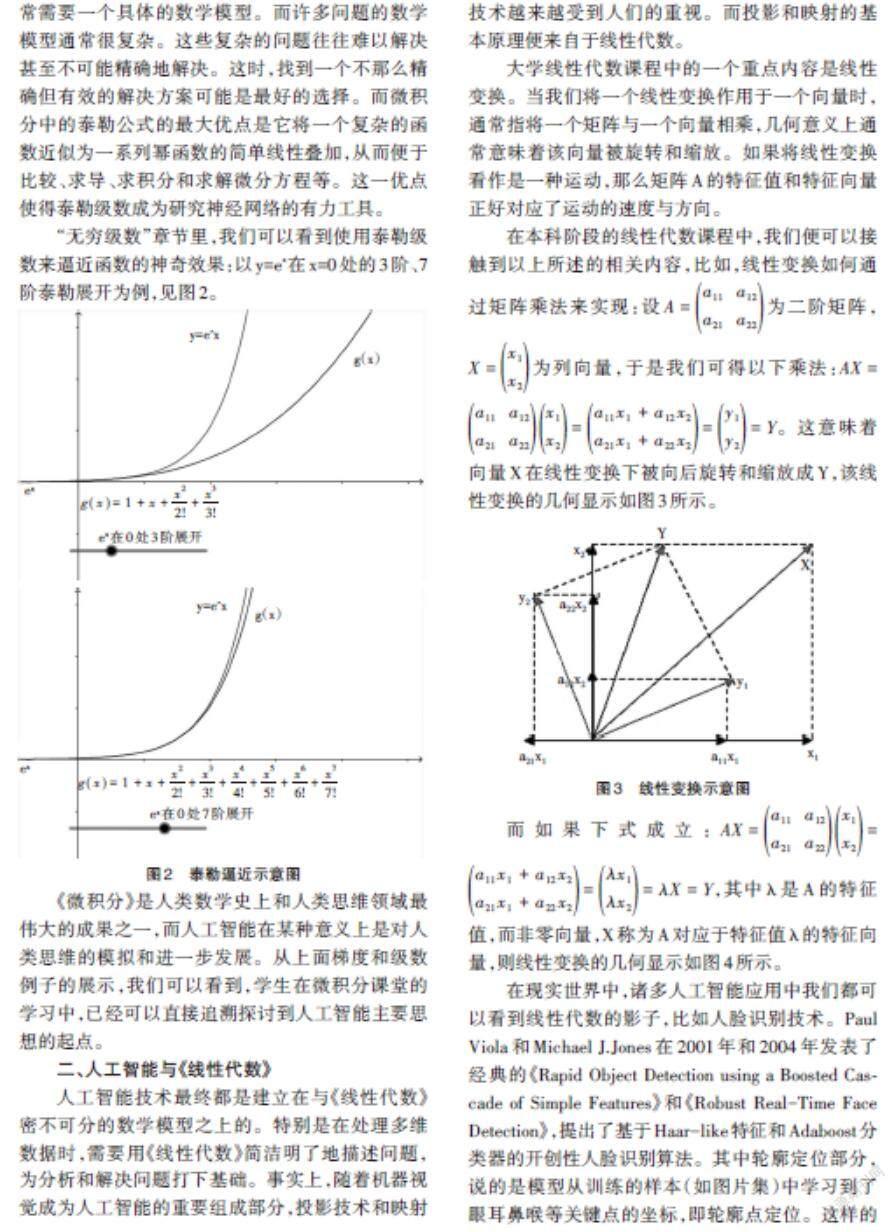
大學線性代數課程中的一個重點內容是線性變換。當我們將一個線性變換作用于一個向量時，通常指將一個矩陣與一個向量相乘，幾何意義上通常意味著該向量被旋轉和縮放。如果將線性變換看作是一種運動，那么矩陣A的特征值和特征向量正好對應了運動的速度與方向。

在本科階段的線性代數課程中，我們便可以接觸到以上所述的相關內容，比如，線性變換如何通過矩陣乘法來實現：設[A=a11? ?a12a21? ?a22]為二階矩陣，[X=x1x2]為列向量，于是我們可得以下乘法：[AX=a11? ?a12a21? ?a22x1x2=a11x1+a12x2a21x1+a22x2=y1y2=Y]。這意味著向量X在線性變換下被向后旋轉和縮放成Y，該線性變換的幾何顯示如圖3所示。

而如果下式成立：[AX=a11? ?a12a21? ?a22x1x2=a11x1+a12x2a21x1+a22x2=λx1λx2=λX=Y]，其中λ是A的特征值，而非零向量，X稱為A對應于特征值λ的特征向量，則線性變換的幾何顯示如圖4所示。

在現實世界中，諸多人工智能應用中我們都可以看到線性代數的影子，比如人臉識別技術。Paul Viola和Michael J.Jones在2001年和2004年發表了經典的《Rapid Object Detection using a Boosted Cascade of Simple Features》和《Robust Real-Time Face Detection》，提出了基于Haar-like特征和Adaboost分類器的開創性人臉識別算法。其中輪廓定位部分，說的是模型從訓練的樣本（如圖片集）中學習到了眼耳鼻喉等關鍵點的坐標，即輪廓點定位。這樣的訓練過程能夠得到人臉的均值輪廓。而一個人的臉部輪廓是可以通過這個均值輪廓進行線性變換得到的。

具體以人臉識別投影過程中需要用到的仿射變換為例。仿射變換一般包括平移變換、旋轉變換、縮放變換、錯切變換、翻轉變換等。簡單舉例如下：

①旋轉變換的向量表示為[xy=cosθ-sinθsinθ-cosθxy]，譬如分別取θ為[π6]、[π4]、[π3]、[π2]，向量[11]即可順時針旋轉相應的角度。

②翻轉變換（以關于y軸的翻轉為例）的向量表示為[xy=-1? ? 0? ?0? ? 1xy]，。

三、人工智能與《概率論與數理統計》

《概率論與數理統計》也是人工智能研究中極其重要的數學基礎。概率論為人工智能提供了隨機性，為預測提供了基礎，而數理統計有助于解釋機器學習算法和數據挖掘的結果。就機器學習而言，它是人工智能的核心，是實現計算機智能化的根本途徑。更具體地說，機器學習是用實例數據或過去的經驗對計算機（智能系統）進行編程，以優化性能標準。在概率論中，過去的經驗是指先驗概率，從中可以根據新的信息獲得后驗概率，而機器學習的最終目標是學習后驗概率。

回到大學數學課程《概率論與數理統計》中的“條件概率”章節部分，我們可以看到連接先驗概率和后驗概率的Bayes公式：

首先假設B1，B2，…，Bn為一個概率空間中的完備事件組，這意味著它們的并集是整個空間，于是有

[PBjA=P（ABj）P（A）=P（ABj）P（Bj）j=1nP（ABj）P（Bj）]

其中[P（A）≠0]

上述重要的Bayes公式通常用于計算后驗概率，公式中的條件概率[P（BjA）]即為后驗概率，而[P（Bj）]是先驗概率。從某種意義上說，[P（ABj）]是新的信息。假設新的信息被加入后，后驗概率[P（BjA）]將成為另一輪利用貝葉斯公式得到新后驗概率的先驗概率。這就是機器學習的工作原理：不斷的學習和不斷的修改。

目前人工智能領域最有效的推理工具之一是貝葉斯網（Bayes Network），它是一種描述變量間不確定因果關系的圖形網絡模型，貝葉斯網就是起源于條件概率和貝葉斯模型。

四、結語

以上三方面的討論展示了大學數學課程與人工智能相關知識有著千絲萬縷的聯系。通過精心的教學設計，將人工智能元素滲透到大學數學課堂是可以實現的。隨著人工智能普及教育在大學教育中的地位越來越突出，人工智能與數學等相關學科、相關課程的交叉融合也將成為未來教育發展的趨勢。數學作為人工智能相關專業的核心基礎課程，對后續的學習研究起著至關重要的作用。在數學課程中滲透人工智能元素，不僅可在人工智能相關的專業素養訓練方面事半功倍，而且還可以激發學生探索研究人工智能知識的興趣。故此，這將是人工智能教育與數學教育的雙贏嘗試。

【參考文獻】

[1]國務院.新一代人工智能發展規劃[EB/OL].[2017-07-20].http：//www.gov.cn/zhengce/content/2017-07/20/content_5211996.htm

[2]教育部.高等學校人工智能創新行動計劃[EB/OL].[2018-04-03].http：//www.moe.gov.cn/srcsite/A16/s7062/201804/t20180410_332722.html

[3]同濟大學數學系.高等數學：第7版（下冊）[M]. 北京：高等教育出版社，2014：106-108.

[4]李武軍，王崇駿，張煒，等.人臉識別研究綜述[J].模式識別與人工智能，2006，19（1）：58-66.

[5]曾文鋒，李樹山，王江安.基于仿射變換模型的圖像配準中的平移、旋轉和縮放[J].紅外與激光工程，2001（1）：18-20，17.

[6]李敏.人工智能數學理論基礎綜述[J]. 物聯網技術，2017，7（7）： 99-102.