基于奇異譜分析的超短期風電功率多步預測

吳堅，項頌，閻誠，吳曉丹，馬繼濤，劉福鎖

（1.國網內蒙古東部電力有限公司，內蒙古呼和浩特 010000；2.東南大學電氣工程學院，江蘇南京210096；3.國電南瑞科技股份有限公司，江蘇南京 211106）

0 引言

風能作為一種高效的清潔能源，具有強烈的隨機性、間歇性和逆負荷性等特點[1]。據統計，2019年全球風電新增和累積裝機容量較2018年同比增長19%和10%[2]。為了降低高滲透率風電對電網帶來的不確定性，提高風電消納能力，實現系統安全穩定運行，準確的風電超短期功率預測具有重要的意義[3]。

風電功率時間序列具有很強的時序特征。風電功率序列預測方法以統計學方法和人工智能算法為主。統計學方法僅依賴時間序列方法進行建模，能夠有效捕捉時間序列中的非線性關系，但存在模型定階和參數估計問題[4]。人工智能算法能夠有效捕捉風電功率時間序列中的非線性關系，但對樣本數據質量依賴較高[5]，其中，最小二乘支持向量機（Least-Squares Support Vector Machine，LSSVM）通過映射關系將原支持向量機模型參數訓練中的非線性問題替換成線性問題，能有效增強模型計算效率，具有較強的泛化能力[6]。對于風電功率序列復雜的波動特性，單一預測模型因受制于樣本維度和數量等因素而具有局限性[7]。

基于數據預處理過程的組合預測模型是提升單一預測方法適應能力和模型精度的重要途徑[8]。通過對原始高頻非線性時間序列進行分解，能夠有效降低序列的復雜程度，采用分解后的子序列分別建立一系列適應其序列特征的預測模型，顯著提升了預測性能。傳統數據預處理方法包括以經驗模態分解（Empirical Mode Decomposition，EMD）[9]和小波分析（Wavelet Decomposition，WD）[10]為基礎衍生出的一系列序列分解方法，但是分解序列結果存在顯著的端點效應和模態混疊現象，極大地增強了預測過程中的難度。而奇異譜分析（Singular Spectrum Analysis，SSA）作為一種非線性時間序列分解重構的分析方法，能夠有效處理復雜序列，無須選取先驗基函數和復雜的運算過程，具有較好的客觀性和自適應性[11]，使其廣泛地應用于各工程學科領域。文獻[12]采用SSA提取風速序列的趨勢成分、振蕩成分和噪聲成分，分別建立預測模型，實現了準確可靠的風速區間預測。但是SSA存在嵌入維度選取困難的問題，過高的嵌入維度導致關鍵序列分量被過度分解為噪聲成分，而較小的嵌入維度無法有效提取序列的關鍵變化特征[13]。

考慮到風電功率時間序列包含大量的時序性和自相關性特征，本文提出了一種基于SSA和LSSVM的組合預測模型。針對SSA嵌入維度存在不確定性的問題，使用Cao方法判別嵌入維度。對于分解得到的子序列分別使用LSSVM進行訓練，通過粒子群優化算法（Particle Swarm Optimization，PSO）確定各子序列的LSSVM模型參數，實現對風電功率的多步預測。引入樣本熵作為分解模型效果度量指標，結合實測數據，驗證了基于SSA的風電功率超短期預測模型在多步預測中的優越性能。

1 整體研究思路

通過對風電功率時間序列進行分解，根據所得到的不同分量的波動特性，分別建立預測模型，以降低預測誤差。采用組合模型進行預測的整體研究思路如圖1所示。

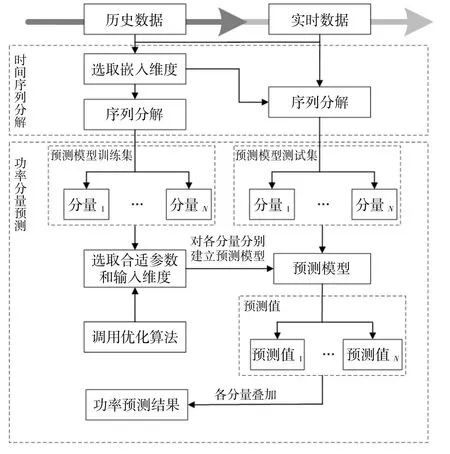
圖1 組合預測模型Fig.1 Diagram of combined forecasting model

首先，基于復雜系統混沌理論，采用Cao方法確定嵌入維度的選取，即分解算法所得到的分量數量，通過對原始訓練樣本進行SSA分解，得到一系列不同時間尺度的分量序列；然后，采用LSSVM分別對其進行訓練，采用PSO優化預測模型的基本參數。類似的，在功率預測階段，將實時采集到的功率數據與歷史數據進行拼接，根據選取的嵌入維度重新進行分解，并采用LSSVM對各分量序列進行預測；最后，疊加不同分量的風電功率序列預測輸出。

2 基于SSA的風電功率序列分解

2.1 SSA原理

SSA是基于奇異值分解的一種序列成分分析方法，與時序預測模型結合能有效提升預測性能。對于具有非線性特征的風電功率序列樣本，通過構建軌跡矩陣、奇異值分解、分組和對角平均化等流程實現風電功率序列的分解[11]。具體流程如下。

提取樣本數量為N的風電歷史功率序列z=[z1，z2，…，zN]，設定SSA的模型嵌入維度為L，將其重構為跡矩陣X：

在此基礎上，可根據奇異值對各子序列進行分組，篩選分解后的各類型分量，剔除諧波分量。在本文中，待預測風電功率序列已經進行了預處理剔除異常數據，因此在SSA階段中不考慮分組的情況。

對角平均化還原時間序列，當X是一個L×K的矩陣，矩陣中元素為xij，令L*=min（L，K），K*=max（L，K），N=L+K-1，且滿足當L＜K時，=xij；否則=xji，對子矩陣Xi進行重構得到的序列[y1，y2，…，yN]可表示為

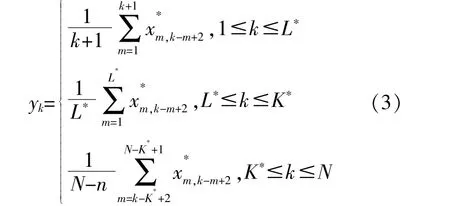
SSA具有很強的非參數性，因此其嵌入維度L決定了模型分解性能。對于復雜波動的風電功率序列，L越大會削弱不同分量之間特征值差異，利于周期規律變化的風電功率的成分提取，但會產生多余分量；L較小能有效反映風電功率序列的波動態勢，但無法充分挖掘分量中蘊含的關鍵信息。L一般通過已知數據進行經驗選取，不能大于給定序列長度的1/2。而風電功率序列兼具短時間尺度的高頻波動特性和長時間尺度變化趨勢，因此合理的L選取具有重要的意義。SSA中構建跡矩陣與混沌系統理論中的相空間重構一致，可借鑒混沌序列相空間重構嵌入維度的選取方法。

2.2 Cao方法

Cao方法具有較強的適應性和計算效率[14]，采用Cao方法計算風電功率序列分解的L步驟如下。

計算不同L下最近鄰點的距離變化值：

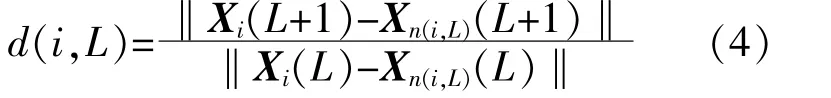
式中：i=1，2，…，N-L；||·||為∞-范數；Xi（L+1）為L+1的第i個重構得到的相空間向量。

對于L+1，Xn（i，M）（L+1）為∞-范數下與Xi（L+1）距離最近的向量，n（i，M）為滿足1≤n（i，M）≤（N-L）的整數。

計算相同L下空間距離波動值的均值：

采用E1（L）監測不同L下E（L）的變化情況：

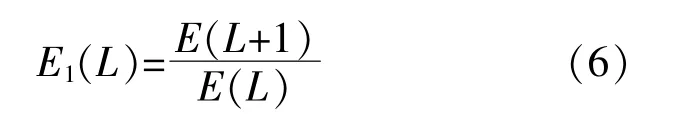
當滿足L＞L0時，對應E1數值停止變化或波動小于一定閾值，得到最小L為L0+1。為了保證L選取的客觀性和合理性，引入E1波動率ei。

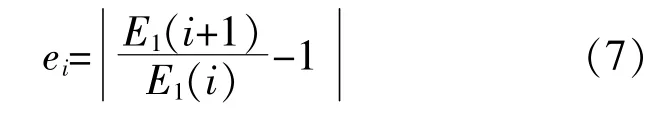
設定閾值e0和波動邊界k，滿足1＜k＜N-1，k為當第一次滿足ei＜e0時的下標。

在此基礎上，定義e：

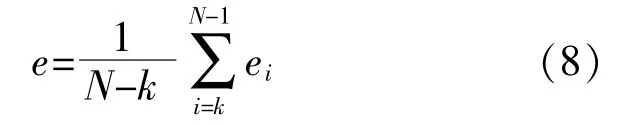
當i+1滿足ei+2＜ei+1＜ei，且ei+1＜e時，得到最佳L=i+1。

2.3 樣本熵

為對比不同分解方法下風電功率序列的分解效果，引入樣本熵描述其復雜程度。樣本熵越大的序列，復雜程度越大。作為一種復雜性度量方法，樣本熵對數據長度不敏感，具有較好的穩定性。對于長度為N的時間序列X=[X（1），X（2），…，X（N）]，其樣本熵計算步驟如下[15]。

基于重構維數m對原風電功率分解子序列進行重構，得到一組m維的空間向量Xm：

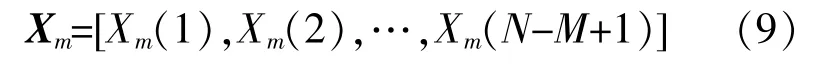
Xm（i）表示為

定義運算Xm（i）和Xm（j）之間距離的絕對值為

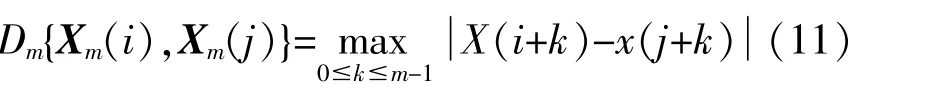
計算Dm{Xm（i），Xm（j）}小于設定相似度閾值r的數量，并記為，Bm。

樣本熵計算式為

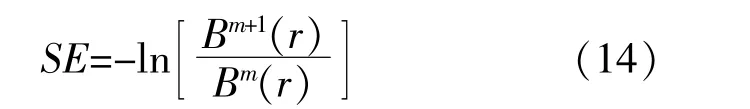
基于一致性原理，通常取樣本熵m為1，r為0.15倍風電功率序列統計標準差[16]。

3 SSA-LSSVM風電功率組合預測模型

3.1 LSSVM原理

本文所研究的風電超短期功率預測，要求風電場內輸出功率序列進行就地和實時的準確預測，因此對于預測模型精度和復雜程度提出了一定的要求。本文通過LSSVM構建風電功率分解后子序列的預測模型，而LSSVM作為支持向量機（Support Vector Machine，SVM）的改進模型，將SVM模型訓練中復雜的二次規劃問題轉變成線性方程組問題[17]，更有利于在工程實際中的應用。可表示為

式中：φ（x）為核空間映射函數；w為權重；b為偏差量。

根據結構風險最小化原則，LSSVM的參數優化模型可表示為

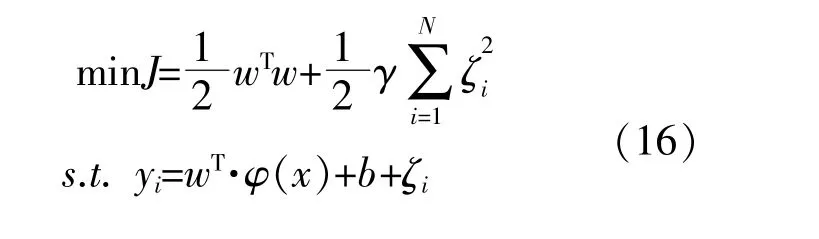
式中：ζ為松弛因子；樣本數量滿足i=1，2，…，N。

構造拉格朗日函數如下：

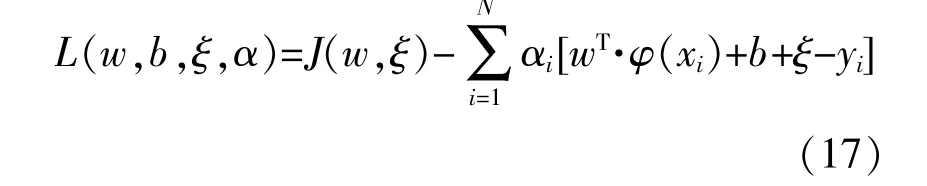
式中：αi為拉格朗日乘子。

根據Karush-Kuhn-Tucker最優條件，得到?L/?ω=0，?L/?b=0，?L/?ξ=0和?L/?αi=0，模型中權值系數w和誤差變量ξ可進行化簡消去，最終得到方程組：

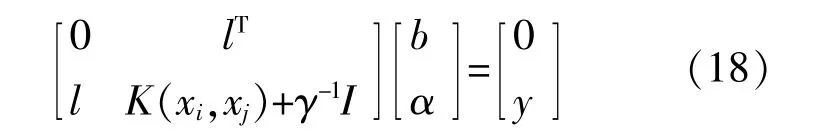
式中：l=[1，1，…，1]T；K（xi，xj）為根據Mercer條件的核函數，文中LSSVM的核函數選取徑向基核函數（Radial Basis Function，RBF）。

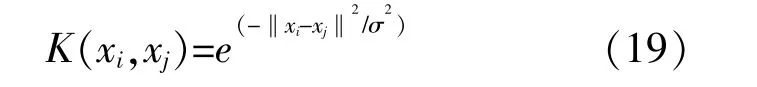
求解得到LSSVM模型為

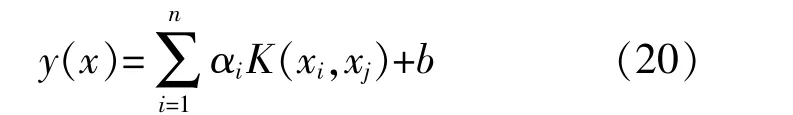
LSSVM模型的性能很大程度取決于懲罰系數γ以及核函數的參數σ的取值，文中采用的PSO為優化算法，以LSSVM輸出和實測值的均方根誤差作為PSO算法的適應度函數，對超參數γ和σ進行尋優，具體原理可見文獻[18]。

3.2 SSA-LSSVM組合預測模型

風電功率序列在短時間尺度存在高非線性和波動性的特征。單一預測方法無法在預測過程中對這些特征進行準確捕捉，因此預測結果普遍存在一定的時延性。本文結合SSA處理非平穩序列的優勢和LSSVM在線高效計算的特點，提出了一種SSA-LSSVM的風電超短期功率組合預測模型。首先采用Cao方法確定功率時間序列的最優L，對原始序列進行SSA分解，得到一系列多時間尺度的固有模態分量（Intrinsic Mode Function，IMF），實現序列的關鍵特征提取；然后分別采用LSSVM對各分量進行訓練，通過PSO優化模型參數；最后通過測試樣本的預測值疊加得到實際風電功率的預測結果。具體步驟如下：

①將功率序列進行訓練集和測試集劃分，以驗證預測模型的泛化能力。初始化模型參數：預測步長T和PSO中的尋優參數，包括粒子種群數量、粒子的位置和速度等；

②在離線模型訓練階段，采取Cao方法確定L，對序列進行SSA分解，采用PSO選取各分量的最佳參數，訓練LSSVM模型；

③在線預測階段，根據T選取測試樣本，對其進行SSA分解，以此輸入LSSVM中生成預測結果。根據T調整LSSVM輸入值，滾動迭代完成該步長下所有分量的預測后，將各分量預測值累加得到真實功率預測值；

④重復步驟③，直到完成整個預測周期的功率預測。

具體功率預測模型流程如圖2所示。

圖2 組合預測模型流程圖Fig.2 Flow chart of combined forecasting model

值得注意的是，采用組合模型通過序列分解的方式進行預測會存在一個誤區，就是對包含訓練樣本和測試樣本的原始風速序列直接進行分解，然后將各分量帶入相應的模型進行預測。因為對含有未來數據的序列進行分解，得到的分量結果本身包含了未來真實值波動的一個趨勢，所以上述方法在實際工程應用中是不可能實現的。采用組合模型進行預測時，必須在每一步預測前對含有當前功率真實值的序列重新進行分解。同時由于分解算法原理上的問題，當待分解的時間序列邊緣的真實值增加到一定數量時，模型輸出的各模態分量會與原始測試樣本產生的分量存在一定程度的畸變。采用EMD方法進行預測時，由于其模態分解數量不可控性，待分解的序列不斷更新，EMD輸出模態分量的數量也會發生改變，而SSA可以克服上述缺點。基于上述考慮，由于每一步預測均須要進行SSA分解以更新各分量的真實值且計算量大，因此組合模型不適用于單步預測和中長期的預測。

為了克服上述問題，文中采用的多步預測模型采用迭代法，即每次只向前預測一步，且每步都采用新得到的預測值而不是實測值來繼續下一步的預測。相較于直接向前預測T步的直接法，迭代法多步預測具有更高的精度[19]。文中通過虛假臨近點法確定LSSVM輸入維度[20]。

4 算例及結果分析

算例采用中國某風電場1.5 MW風機在2015年6月19-26日SCADA采集的功率序列為實驗樣本，輸入風速采樣間隔為10 min，共計1 152個功率采樣點，選取前1 008個采樣點為模型實驗樣本，后144個點為測試樣本。測試前已進行數據清洗，故在SSA分析過程中不再考慮對樣本重構分量的篩選。實驗在MATLAB 2019a平臺上進行。選取Cao方法維度篩選閾值e0=0.01，Cao方法中所定義E1的波動情況和不同維度下最大最小特征值的比值λmax/λmin如圖3所示。

圖3 Cao方法選取嵌入維度Fig.3 Select embedding dimension using Cao method

由圖3可以看出，當L達到13時，E1停止波動，同時λmax/λmin與L呈線性遞增關系上漲。L過大會造成計算量顯著增加和關鍵特征序列被淹沒，而Cao方法不須要依賴經驗，可確定最佳L。基于此，對訓練樣本進行SSA分解，構成13個特征值遞減的模態分量，如圖4所示。由圖可以看出，SSA分量為1的奇異值顯著高于其他分量，說明該分量對原風電功率軌跡矩陣貢獻值最大。

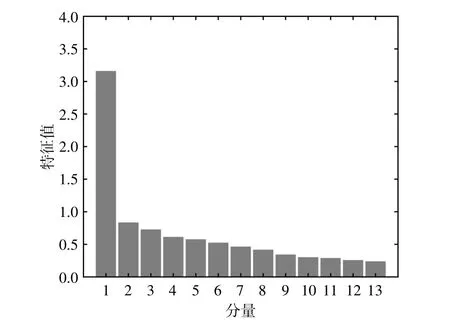
圖4 SSA分解序列奇異值Fig.4 Comparison of Singular value of SSA decomposition sequence

為了驗證所提模型的預測性能，本文采用PSO-LSSVM[18]和以EMD方法、完備經驗模態分解（Ensemble EMD，EEMD）以及改進總體完備經驗模態分解（Improved Complete Ensemble EMD，ICEEMD）[21]為基礎，與LSSVM結合的預測方法進行對比分析，以下分別稱為EMD-LSSVM，EEMD-LSSVM和ICEEMD-LSSVM方法。EEMD在EMD的基礎上通過增加白噪聲降低EMD的模態混疊現象。進一步，ICEEMD通過利用添加自適應白噪聲和選取各模態分量當前的局部均值以重新定義真實模態的方式對EMD方法進行改進，克服了虛假模態和分量存在延遲特性等問題，是當前EMD一類算法應用于預測模型中的典型代表，具體算法流程可參見文獻[22]。

樣本熵在度量低維數據復雜程度上具有巨大的優勢，通過計算可得原始時間序列樣本熵為1.606 9，各方法樣本熵對比結果如表1所示。

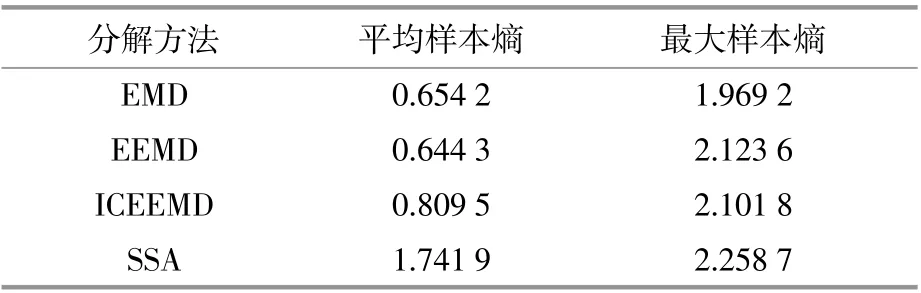
表1 不同分解方法樣本熵計算結果Table 1 Calculation results of sample entropy for different decomposition methods

表1顯示經SSA分解后的各分量信號仍保持較高的復雜性特征，而只通過EMD類方法分解得到的分量平均樣本熵遠低于原始序列樣本熵。為了量化分析不同預測方法和步長下多步預測時的預測精度，本文采用歸一化均方根誤差（Normalized Root-Mean-Squared Error，NRMSE）、歸一化絕對平均誤差（Normalized Mean Absolute Error，NMAE）和歸一化絕對誤差（Normalized Absolute Error，NAE），定義如下：

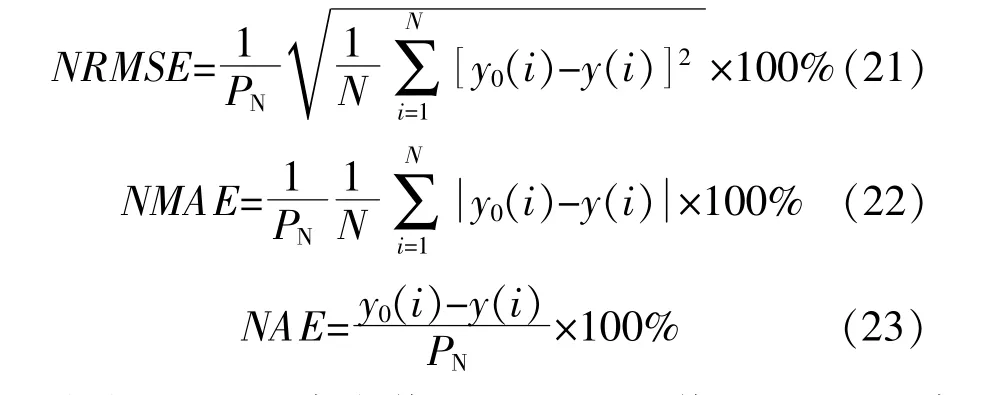
式中：y0（i）為真實值；y（i）為預測值；N為預測序列總長度；PN為風機裝機容量。

預測模型的四步預測結果及其對應的不同預測方式下的NAE如圖5所示。

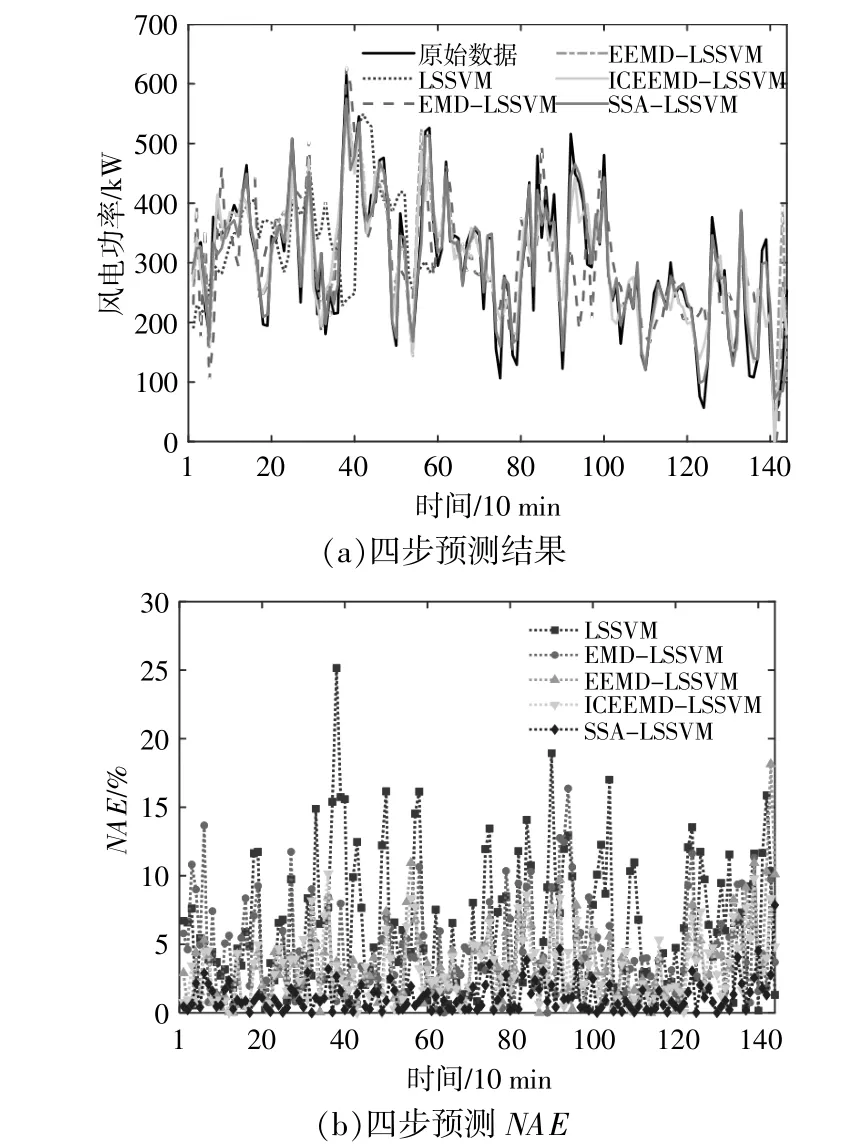
圖5 四步預測結果及誤差Fig.5 Curves of four-step wind power prediction results and error

為了驗證文中所提方法的有效性，本文將直接通過LSSVM預測和以EMD類分解方法為基礎的LSSVM預測結果與所提出的方法進行對比。由圖5可以看出，SSA-LSSVM方法能夠在多步預測過程中很好地捕捉原始序列的變化趨勢，精度較未采用序列分解而直接預測的結果有顯著的提升。由于對時間序列的充分分解，原來具有高頻波動特征的風電功率序列的復雜程度被充分降低，有利于預測模型的擬合。EMD類方法無法主觀設定分解維數，因此在預測過程中會出現分解維度突變情況，適應性較差。ICEEMD相較于EMD和EEMD方法，克服了數據預處理過程中的端點效應，但是在風電功率突變點，預測結果與SSALSSVM方法預測結果變化趨勢有明顯差別，說明單獨的ICEEMD模態分解方法無法對原序列的多時間尺度分量實現充分的分解，整體預測精度低于SSA-LSSVM方法。而只采用LSSVM的方法受訓練樣本容量的限制，超短期預測結果中存在多處滯后現象，預測效果最差。在四步預測步長下，SSA-LSSVM方法相對誤差始終維持在一個較低水平，說明組合模型能有效提升機器學習方法對時間序列的擬合水平。SSA方法能夠很好地挖掘原始時間序列中的關鍵特征，而LSSVM方法可以模擬序列分解得到非線性特性變化。

圖6給出了不同預測方法在各預測步長下的誤差性能指標，SSA-LSSVM預測模型在不同預測步長下的預測誤差均小于其他方法，隨著預測步長的提升，同一預測模型的預測性能也會逐漸下降。單一LSSVM預測性能最差，相較于傳統EMD方法，采用EEMD-LSSVM和ICEEMD-LSSVM方法有效降低了模型預測誤差，但是對預測性能的改善作用十分有限，隨著預測步長的增大，這一改善作用會逐漸減弱。在各預測步長下，基于SSA的預測方法的NRMSE和NMAE始終低于EMD類方法誤差性能指標，說明與EMD類方法相比，SSA方法對序列關鍵特征分量提取能力更強，輸出分量質量較高，有利于LSSVM學習序列特征，提升組合模型的預測精度。

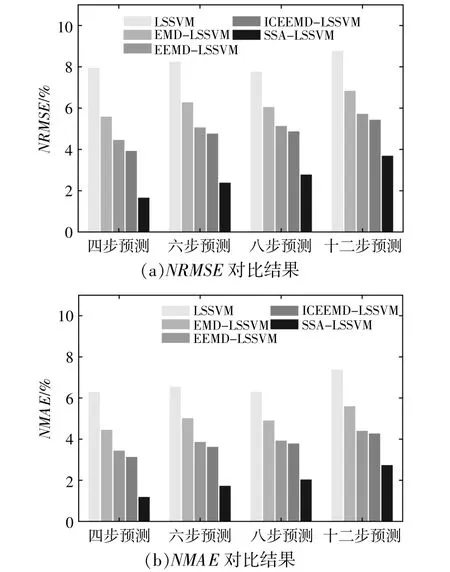
圖6 預測誤差性能指標Fig.6 Prediction error performance index

5 結論

針對風電功率序列復雜的波動特性，本文提出了一種基于SSA的超短期風電功率組合多步預測方法。算例對比研究結果表明：

①通過Cao方法確定SSA的最佳嵌入維度，有效避免了人為因素的影響以及單純追求預測結果而造成的序列特征被淹沒和計算量暴增等問題；

②SSA具有直接提取風電功率序列不同成分的能力，與其他數據預處理方法相比，分解后序列平均樣本熵最大，有效保留了原始序列關鍵特征；

③所提基于SSA的預測模型能夠獲取時間序列中的時序演變特征和波動趨勢，有效提升了不同步長下的預測精度，計算效率更高。