半張量積在線性映射中的應(yīng)用

李東方，劉會(huì)彩，張 錦

(1.許昌電氣職業(yè)學(xué)院公共教學(xué)部，許昌 461000；2.聊城大學(xué)數(shù)學(xué)科學(xué)學(xué)院，聊城 252059)

文[1]中，程代展給出了一種新的矩陣乘法——矩陣的左半張量積，并給出了它在Morgan問(wèn)題中的應(yīng)用.隨后，程代展研究員把它應(yīng)用于幾何、代數(shù)、邏輯、圖論、動(dòng)態(tài)系統(tǒng)、故障檢測(cè)、模糊控制、非線性控制等領(lǐng)域，效果顯著，取得了豐碩的成果，并把部分成果總結(jié)于文獻(xiàn)[2-3]中。在文獻(xiàn)[4]中，程代展、齊洪勝、賀風(fēng)華等把半張量積方法應(yīng)用于有限集上的映射表示及動(dòng)態(tài)系統(tǒng)的演化規(guī)律及控制，利用新的工具，從新的角度審視，給出了一系列新的結(jié)果。在文獻(xiàn)[5-13]中，程研究員等把半張量積應(yīng)用于布爾網(wǎng)絡(luò)控制，先構(gòu)造了它的代數(shù)形式，然后再返回邏輯形式。這與傳統(tǒng)的直接構(gòu)造布爾網(wǎng)絡(luò)的邏輯動(dòng)態(tài)方程的方法截然不同。

本文把程代展研究員定義的矩陣左半張量積應(yīng)用于線性映射中，從新的視角解決了幾類復(fù)雜的線性映射的矩陣表示問(wèn)題，讓我們看到了用半張量積研究線性映射的優(yōu)越性。

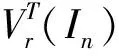
1 預(yù)備知識(shí)

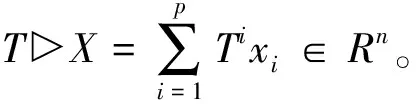
給定矩陣A∈Mm×n,B∈Mp×q，如果n=tp，我們記為A?tB；反之，如果nt=p，我們記為AtB。那么左半張量積有如下等價(jià)定義：

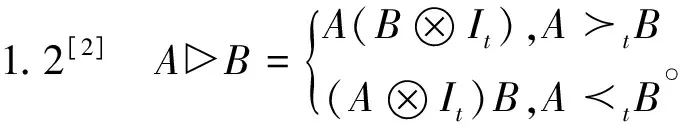
定義1.3[2]換位矩陣W[m,n]是一個(gè)mn×mn矩陣，定義如下：它的行和列都是有雙指標(biāo)(i,j)標(biāo)注，列是按照索引Id(i,j;m,n)排列，行是按照索引Id(J,I;n,m)排列，并且位于[(I,J),(i,j)]上的元素的值為

可以看出換位矩陣W[m,n]總是一個(gè)正交矩陣。

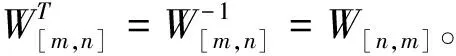
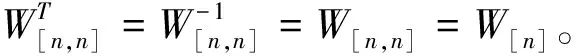
定理1.2[2]設(shè)A∈Mm×n,X∈Mn×q,Y∈Mp×m，則有Vr(AX)=A?Vr(X)，Vc(YA)=AT?Vc(Y)。

定理1.3設(shè)A是一個(gè)m×n維矩陣，則有(1)Vr(A)=Vc(AT),Vc(A)=Vr(AT)；

(2)W[m,n]Vr(A)=Vc(A),W[n,m]Vc(A)=Vr(A)。

推論1設(shè)A是一個(gè)m×n維矩陣，則有Vc(AT)=W[n,m]Vc(A),Vr(AT)=W[m,n]Vr(A)。

證明由定理1.3直接可得。

定理1.4[2]設(shè)A∈Mm×n,B∈Mp×q，則有A?B=W[p,m]?B?W[m,q]?A=(Im?B)?A。

特別地，有W[p,m]?B?W[m,q]=(Im?B)。

定理1.5[2]設(shè)A∈Mm×n,B∈Mp×q，則有

(1)(Ip?A)W[n,p]=W[m,p](A?Ip)；(2)W[m,p](A?B)W[q,n]=(B?A)。

定理1.6[4]設(shè)A∈Mm×n,B∈Mp×q,C∈Mn×r，以及D∈Mq×s。那么(A?B)(C?D)=(AC)?(BD)。

特別地，有(A?Ip)(In?D)=A?B。

在文獻(xiàn)[2-3]中已表明左半張量積是普通矩陣乘法的推廣，普通矩陣乘法是它的一種特殊情況。除非為了強(qiáng)調(diào)左半張量積，一般情況下我們省略半張量積符號(hào)?。

2 主要結(jié)論

設(shè)X∈Mn×p，我們考慮一般的線性映射ρ:Mn×p→Mm×q，定義如下：

X→AXB+CXTD，

其中，A∈Mm×n,B∈Mp×q,C∈Mm×p,D∈Mn×q。

定理2.1設(shè)A∈Mm×n,X∈Mn×p，對(duì)于映射ρ:X→AX，則其行展開表示是Vr(ρ(X))=(A?Ip)Vr(X)。

證明由定理1.2可得：Vr(ρ(X))=Vr(AX)=A?Vr(X)=(A?Ip)Vr(X)。

定理2.2設(shè)X∈Mn×p,B∈Mp×q,對(duì)于映射ρ:X→XB，則其行展開表示是Vr(ρ(X))=(In?BT)Vr(X)。

證明由定理1.2，1.3及1.5可得：

Vr(ρ(X))=Vr(XB)=Vc(XB)T=Vc(BTXT)=W[q,n]Vr(BTXT)=W[q,n](BT?In)Vr(XT)=W[q,n](BT?In)Vc(X)=W[q,n](BT?In)W[n,p]

Vr(X)=(In?BT)Vr(X)。

定理2.3設(shè)A∈Mm×n,X∈Mn×p,B∈Mp×q,對(duì)于復(fù)合映射ρ:X→AXB，則其行展開表示是

Vr(ρ(X))=(A?BT)Vr(X)

證明由定理2.1，2.2及1.6可得：

Vr(ρ(X))=Vr(AXB)=(A?Iq)Vr(XB)=(A?Iq)(In?BT)Vr(X)=(A?BT)Vr(X)

證明定理2.3中令B=A-1可得。

定理2.4設(shè)C∈Mm×p,X∈Mn×p，對(duì)于映射ρ:X→CXT，則其行展開表示是

Vr(ρ(X))=(C?In)W[n,p]Vr(X)

證明由定理1.2，1.3可得：

Vr(ρ(X))=Vr(CXT)=C?Vr(XT)=(C?In)Vr(XT)=(C?In)W[n,p]Vc(XT)=(C?In)W[n,p]Vr(X)

定理2.5設(shè)D∈Mn×q,X∈Mn×p，對(duì)于映射ρ:X→XTD，則其行展開表示是

Vr(ρ(X))=(Ip?DT)W[n,p]Vr(X)

證明由定理1.3，2.1可得：

Vr(ρ(X))=Vr(XTD)=Vc(DTX)=W[q,p]

Vr(DTX)=W[q,p](DT?Ip)Vr(X)=W[q,p](DT?Ip)Vc(XT)=W[q,p](DT?Ip)W[p,n]W[n,p]

Vc(XT)=(Ip?DT)W[n,p]Vc(XT)=(Ip?DT)W[n,p]Vr(X)。

定理2.6設(shè)C∈Mm×p,X∈Mn×p,D∈Mn×q,對(duì)于復(fù)合映射ρ:X→CXTD，則其行展開表示是

Vr(ρ(X))=(C?DT)W[n,p]Vr(X)

證明由定理2.4，2.5及1.6可得：

Vr(ρ(X))=Vr(CXTD)=(C?Iq)Vr(XTD)=(C?Iq)(Ip?DT)W[n,p]Vr(X)=(C?DT)W[n,p]Vr(X)

推論3(Lyapunov映射)設(shè)A∈Mn×n考慮映射LA:Mn→Mn，定義如下：LA(X)=AX+XAT，則其行展開表示是Vr(LA(X))=(A?I+I?A)Vr(X)。

證明由定理2.1，2.2可得：

Vr(LA(X))=Vr(AX+XAT)=Vr(AX)+Vr(XAT)=(A?I)Vr(X)+(I?A)Vr(X)=(A?I+I?A)Vr(X)。

推論4(辛映射)設(shè)A∈Mn×n考慮映射SA:Mn→Mn，定義如下：SA(X)=AX+XTA，則其行展開表示是Vr(SA(X))=(A?I+(I?AT)W[n])Vr(X)。

證明由定理2.1，2.5可得：

Vr(SA(X))=Vr(AX+XTA)=Vr(AX)+Vr(XTA)=(A?I)Vr(X)+(I?AT)W[n]Vr(X)=(A?I+(I?AT)W[n])Vr(X)

推論5(伴隨映射)設(shè)A∈Mn×n考慮映射adA:Mn→Mn，定義如下：adA(X)=AX-XA，則其行展開表示是Vr(adA(X))=(A?I-I?AT)Vr(X)。

證明由定理2.1，2.2可得：

Vr(adA(X))=Vr(AX-XA)=Vr(AX)-Vr(XA)=(A?I)Vr(X)-(I?AT)Vr(X)=(A?I-I?AT)Vr(X)

定理2.7設(shè)A∈Mn×n,X∈Mn×n,對(duì)于復(fù)合映射ρ:X→XAX，則其行展開表示是

Vr(ρ(X))=(In?VrT(In))(AT?In)

證明Vr(ρ(X))=Vr(XAX)=XA?Vr(X)

對(duì)于XA，我們有

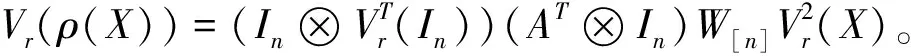
定理2.8設(shè)A,B,C,X∈Mn×n，對(duì)于復(fù)合映射ρ:X→AXBXC，則其行展開表示是

證明由定理2.3可得

Vr(ρ(X))=Vr(AXBXC)=(A?CT)?

Vr(XBX)=(A?CT)?XB?Vr(X)

對(duì)于XB，我們有

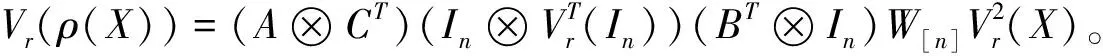
本文討論的幾種線性映射都是按矩陣的行展開Vr(X)表示。相應(yīng)的，對(duì)于線性映射的列展開Vc(X)表示也有類似的結(jié)論成立，這里不再贅述。

3 應(yīng)用

作為應(yīng)用，下面我們給出計(jì)算一般線性群的李代數(shù)。一般線性群記作GL(n,R)，把它看作Rn×n的一個(gè)開子集，它是一個(gè)解析流形。在這個(gè)流形結(jié)構(gòu)下，乘法和逆運(yùn)算都是解析的。因此，它是一個(gè)李群。李群的所有左不變向量場(chǎng)構(gòu)成它的李代數(shù)。

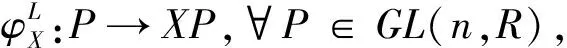
又因?yàn)镕(X)是左不變的，A左平移到X的向量正好是F在該點(diǎn)的值，故

上式最后一個(gè)等號(hào)由定理2.1得到。因此，F(xiàn)(X)在X的矩陣形式是XA。

接著給定兩個(gè)左不變向量場(chǎng)F和W，分別由A和B生成。由上面的過(guò)程可知，F(xiàn)和W的矩陣形式分別是F(X)=XA和W(X)=XB。利用定理2.1，在向量形式下，它們可以分別表示成

F(x)=(In?AT)x，W(x)=(In?BT)x

這里x=Vr(X)。

根據(jù)公式[14]

我們有

[F(x),W(x)]=(In?BT)(In?AT)x-(In?AT)(In?BT)x=((In?BT)(In?AT)-(In?AT)(In?BT))x=(In?BTAT-In?ATBT)x=(In?(BTAT-ATBT))x=(In?(AB-BA)T)x

再次利用定理2.1，[F(x),W(x)]的矩陣表示是(AB-BA)X，也就是由AB-BA生成的左不變向量場(chǎng)。因此，李群GL(n,R)的李代數(shù)gl(n,R)上的李括號(hào)是[A,B]=AB-BA。