能量和角動量對磁化γ時空中帶電粒子混沌運動的影響

胡愛榮，黃國慶

(南昌大學a.理學院；b.建筑工程學院，江西 南昌 330031)

2016年2月11日美國科研人員宣布利用激光干涉引力波天文臺(LIGO)于2015年9月首次探測到雙黑洞在13億年前并合產生的引力波抵達地球[1]。2019年4月10日，借助分布于全球不同地區的8個射電望遠鏡陣列組成的虛擬望遠鏡網絡(EHT)，人類第一次看到黑洞(位于室女座一個巨橢圓星系M87的中心，距離地球5500萬光年，質量約為太陽的65億倍)的視界面[2]。兩大轟動世界的重要發現，有力地支持了愛因斯坦的廣義相對論。2017年、2019年和2020年，引力與天體物理領域四年內三次獲得諾貝爾物理學獎，不僅是對科學家們工作的肯定，更是人類對宇宙認知突破的認可。

眾所周知，1915—1916年愛因斯坦提出并發表了廣義相對論，指出萬有引力是時空彎曲的幾何效應。通過引入黎曼幾何作為數學工具，愛因斯坦最終給出了廣義相對論的基本方程——場方程，并預言引力波的存在。廣義相對論完全顛覆了傳統時空觀，將天體力學帶到了后牛頓時代。此后數十年，科學家們通過求解廣義相對論場方程，得出有封閉邊界(視界)的時空結構，物理學家惠勒命名為“黑洞”。Schwarzschild黑洞、Reissner-Nordstr?m黑洞、Kerr黑洞等都是愛因斯坦場方程的經典解。

黑洞由于其特殊性，本身的信息并不多。霍金等[3]研究證明，最終出現的穩態黑洞僅有非常有限的幾個類型，僅用質量、自旋和電荷就可以完整描述，即“黑洞無毛”。“物質告訴時空如何彎曲，時空告訴物質如何運動”。科學家于是反其道而行之，通過研究測試粒子運動的動力學特征來了解黑洞的性質。

混沌[4-6]是發生在非線性系統的一種特殊的運動狀態，只有滿足一定的條件才可能出現，服從確定性規律但具有隨機性。經典黑洞周圍的時空雖然是高度非線性的，由于有足夠多的積分來分離測試粒子的運動方程，因此是嚴格可積、有序的。但對于這樣的系統而言，內在的一種隨機性——混沌一直存在，只要引入微擾，時空幾何的可積性將會被破壞，混沌運動可能發生。相對黑洞這一類致密天體而言，可能的“微擾”其實也是非常巨大的，可靠來源通常考慮：產生引力作用的質量物質，等效于離心效應的自旋運動[7-9]，以及具有電磁作用的磁場分布。許多學者做了大量相關研究工作。例如具有單極核和偶極子、四極等的相對論核-殼系統[10-11]、環繞黑洞的物質(如吸積盤、質量暈或環)[12]，粒子運動受物質引力的影響，混沌可能會發生。在Schwarzschild黑洞[13]、Kerr黑洞[14]的粒子自旋，使得運動的可積性被破壞，運動由有序過渡到混沌。帶電粒子在電磁場和引力時空中運動時，電磁力的變化對混沌程度起著重要作用[15-17]。如果磁場破壞原始時空的引力效應，即使中性粒子在磁化的Ernst時空也可能發生混沌運動[18-19]。

本文主要研究帶電粒子在磁化的γ時空中的動力學行為。先由時空的度規矩陣和外加磁場的四維矢勢推導出測試粒子在該磁化時空中的哈密頓函數，從而得到粒子運動的正則方程。然后根據速度流形改正法計算粒子在多組初值條件下的數值，描繪出相空間的龐加萊截面圖，利用KAM環是否規則判斷粒子的運動是否存在混沌現象，以此了解不同的能量或角動量對混沌的影響。最后對能量和角動量影響測試粒子混沌運動的機制進行理論分析。

1 模型

γ時空的度規在Erez-Rosen坐標系中可以用對角線元素[20]表示

ds2=gαβdxαdxβ=-F1dt2+F1-1[F2dr2+F3dθ2+(r2-2mr)sin2θdφ2]

(1)

其中的系數函數表示如下

(2)

式(2)中m是球對稱的史瓦西黑洞質量，類史瓦西黑洞的質量為M=γm，γ為形變參量。可以驗證，取γ=1就是經典的史瓦西黑洞；如果γ偏離1則代表引力源為長或扁的橢球型黑洞。

為了讓理論分析更具有遍性，我們對相關物理量進行無量綱化處理，時空尺度都以質量m為單位，x→xm,τ→τm。如果測算出某天體的質量相當于多少個太陽質量，其余的參數信息即可按相應比例確定。無量綱化處理后，γ時空的拉格朗日量可表達為：

(3)

其中x的上標α和β取{0,1,2,3}分別代表史瓦西坐標{x0,x1,x2,x3}={t,r,θ,φ}。式(3)中系數函數可簡化為

(4)

對應的哈密頓量為

(5)

若幾何時空附加一個軸對稱的外部磁場，其四維矢勢

(6)

設測試粒子所帶電荷量為q，該帶電粒子在時空引力和電磁力的共同作用下運動，其協變動量服從關系式

pα=Pα+qAα

(7)

注意到γ時空及磁場分布都具有軸對稱特點，且哈密頓H表達式中不顯含參量t和φ，因此該哈密頓系統存在兩個守恒常量

(8)

(9)

采用能量E和角動量L表示的哈密頓量為

(10)

顯然，粒子的運動遵守正則方程：

(11)

本文中的拉格朗日量與哈密頓量均沒有截斷，表達式完整，兩者是等價的。因此系統的哈密頓量也是個守恒量，滿足

H=-1/2

(12)

在磁化γ時空中，由式(10)和(12)可得

E2-V2

(13)

其中赤道面(取θ=π/2)上的有效勢，記作

V2=F1+

(14)

有效勢可以提供關于測試粒子運動的有價值的動力學總體信息，特別是通過對粒子在赤道平面上徑向運動有效勢的分析，可以了解粒子在束縛軌道的運動所需能量、允許運動的區域邊界，以及由有效勢的極小值確定穩定圓軌道、最內層穩定圓軌道等信息。其中最內層穩定圓軌道代表吸積盤的內部邊界，通常表明候選黑洞存在。許多學者非常關注有效勢。Benavides-Gallego[21]分析了粒子在磁化γ時空中的有效勢，并研究了粒子做圓周運動的能量與角動量及碰撞行為。Deng討論了quantum-corrected Schwarzschild黑洞[22]和DMPR brane-world黑洞[23]等的視界和粒子的周期性束縛軌道。Yi & Wu[24]研究發現在磁化Schwarzschild黑洞中帶電粒子運動的有效勢曲線受到形變參數影響，最內層穩定圓軌道半徑隨正形變的增大減小。有效勢發生改變，對測試粒子的運動具有明顯影響。

2 數值計算結果

注意到式(13)中有效勢V2的曲線形狀與形變參數γ、電磁參數β(=qB)及角動量L有關，因此研究能量的影響時，保持參量γ、β及L均不變，有效勢曲線也就由V2(r)確定了。有效勢曲線的變化，可體現粒子在黑洞外不同位置所受到作用力的強弱。例如，圖1(a)中β=0的有效勢曲線，在內層穩定圓軌道(曲線最小值對應的位置)之外，有效勢的數值隨著距離的增大而逐漸增加，代表隨著距離黑洞越遠對應的引力越小。此外在圖1(a)-(c)中,通過對比可以看到β>0時的有效勢比β=0(即無外加磁場，只有中心天體的引力作用，運動粒子不受磁場力)的數值較小，說明該情況下運動粒子受到的磁場力與黑洞的引力方向相同，磁場力具有引力效應。而改變粒子所帶電荷的電性，或外加磁場反向時，可取β<0，此時磁場力也反向，導致有效勢有所增加。

就本文研究的側重問題，下面主要分析角動量對有效勢的影響，其中形變參量γ和電磁參量β來自后續關于角動量對混沌運動影響的討論中所取的值。對同一個時空形變參量γ而言，保持相同的電磁參量β不變，角動量L的增加導致有效勢曲線隨之升高，如圖2(a)-(f)所示，這意味著具有離心效果的角動量L增加，加劇了磁場力的引力效應，帶電粒子受到的約束合力減小。

圖1 粒子運動的有效勢與電磁參量的關系曲線

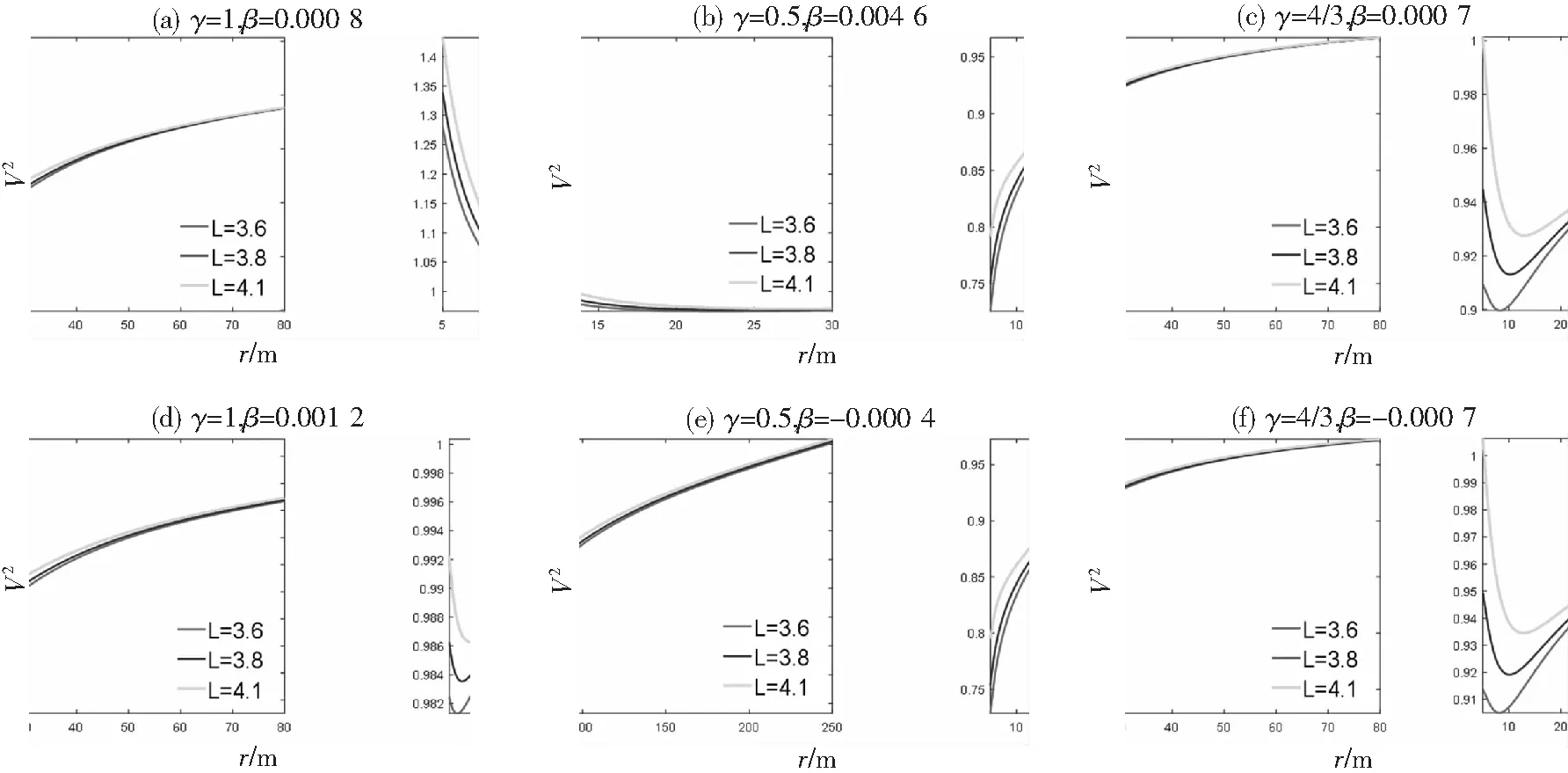
圖2 粒子運動的有效勢與角動量的關系曲線

首先利用數值計算結果來考察能量對粒子運動狀態的影響。對史瓦西黑洞取γ=1，選擇測試粒子的電磁參量為β=0.000 95，角動量L=3.6也保持不變。圖3(a)中粒子的能量取E=0.990 0，龐加萊截面圖中規則的KAM環顯示粒子的運動是有序的。圖3(b)中能量增加為E=0.991 0，所選取的幾條軌道初始值不變。可以看到，粒子的一條軌道(紅色標記)對應的龐加萊截面由規則的閉合曲線變成有輪廓的散點，代表粒子已經由有序的擬周期運動變為混沌運動；另一條(藍色標記)則變成∞字型交錯的曲線，混沌程度更深。進一步增加能量到E=0.992 0時，圖3(c)顯示更多條軌道(紅色、藍色、玫紅色標記)的有序性被破壞，粒子運動的混沌程度加深。另取形變參數γ=0.5和γ=4/3，粒子運動對應的龐加萊截面分別如圖3(d)-(f)和圖3(g)-(i)所示。顯然，隨著粒子的能量不斷增加，粒子的混沌運動越來越明顯。

當β<0時,由于該情況下有效勢的數值比β≥0時更大。且根據式(13)可知，同等條件下粒子運動所需能量E應比β>0時的能量值更高，因此我們選擇相對較高的能量值，分別為E=0.999 2，0.999 3和0.999 4。對處于形變參數為γ=1,0.5和γ=4/3時空中的測試粒子進行對比，對應的龐加萊截面如圖3(j)-(r)所示。可以發現粒子的運動也具有如β>0情形時同樣的演化規律，混沌程度隨著粒子能量的增加而增加。

圖3 不同能量E對粒子混沌運動的影響

其次考察角動量對粒子運動狀態的影響。對γ=1取電磁參量β=0.000 8，給定能量E=0.991 7保持不變。圖4(a)中角動量取L=3.6，龐加萊截面圖中顯示其中有兩條軌道(紅色、玫紅色標記)是混沌的。所選取的幾條軌道初始值不變，圖4(b)中角動量增加為L=3.8，其中的一條軌道運動(玫紅色標記)的混沌程度減弱。進一步增加角動量到L=4.1時，圖4(c)中規則的KAM環顯示這幾條軌道的粒子運動均已回歸有序。形變參數取γ=0.5對應的龐加萊截面如圖4(d)-(f)所示，對應能量及電磁參量標示圖中，也可以看到隨著粒子的角動量增加，混沌運動逐漸減弱。而對γ=4/3，混沌運動(紅色標記)即使不能完全消失，也有不同程度的減弱(玫紅色標記)，如圖4(g)-(i)所示。當β<0，即電荷電性相反或磁場反向時，如圖4(j)-(r)所示，粒子的混沌運動均隨著角動量增加而逐漸減弱。

圖4 不同角動量L對粒子混沌運動的影響

3 結論及理論解釋

上述演化規律表明，能量或角動量的改變都會影響到帶電粒子的混沌運動。下面我們就能量和角動量對粒子混沌運動的影響機制進行理論分析。γ時空中引入外加磁場，帶電粒子運動會受到磁場力的作用，外加磁場也具有引力效應。無論磁場力與黑洞的引力方向相同或相反，均可使測試粒子偏離有序軌道運動，破壞原來時空的有序性，導致混沌發生。

在廣義相對論中，雖然沒有如經典力學中明確動能、勢能的區別，然而一般相對論問題中仍然可得到類似于經典的勢能函數，如帶電粒子在赤道平面上徑向運動的有效勢，通過它可以很容易了解動力學的總體信息。研究能量的影響時，保持參量γ、β及L均不變，有效勢V2(r)曲線關系不變，相同參數情況下受力不變。因此軌道初值條件我們選擇相同的r值，而增加能量E的取值，式(12)的右函數數值隨之增大，意味著帶電粒子具有更大的運動能力打破黑洞引力束縛下的有序狀態，演化為混沌運動。

對于角動量對混沌運動的影響，保持相同的參量γ、β不變，而能量E維持不變，當有效勢曲線隨角動量L的增加而升高，式(12)的右函數隨之減小，若帶電粒子有限的運動能力不足以破壞引力的束縛，其運動就可能回歸到有序狀態。