模糊Cut集

饒三平，劉芝秀

(南昌工程學院理學院,江西 南昌 330099)

完全分配格作為某類完備集環的閉子格，在文[1]中，由Raney給出。之后，Raney在文[2]中，從序的角度，給出了完全分配格的一個等價刻畫。從那以后，Hofmann[3]和Lawson[4]從同構和對偶的角度也對它進行了研究。

由于形式概念分析和完備格之間的關系，基于完備剩余格，文[5]想從模糊視覺下，研究這種對應關系，首先引入模糊完備格的概念，把它作為經典完備格的一般推廣。此后，Zhang和Xie對模糊完備格和一些模糊偏序集的完備化進行了大量的研究[6]。從范疇的角度， Lai和Zhang提出了完全分配的Ω-格[7]。Stubble等人基于更為一般的真值結構，對它進行了研究[8]。

由于模糊完全分配格的抽象性，所給的例子并不多，大部分是對模糊domain的研究[9-11]。對它也沒有一個非常具體的認識。基于此，本文想通過Cut集來給出模糊完全分配格一個例子，豐富模糊完全分配格理論。

1 預備知識

本文選取完備剩余格作為格值，完備剩余格L是一種代數結構，它滿足：

(1) (L,∧,∨,*,→,0,1)是完備格，最小元為0，最大元為1；

(2) (L,*,1)是可交換的monoid,其中1是單位元，即?a∈L,a*1=a;

(3) *,→構成Galois聯絡，即?a,b,c∈L,a*b≤c?a≤b→c。

有關詳細完備剩余格的知識可參考文獻[12]，若無特別聲明，本文中L表示完備剩余格。下面列出運算*,→的一些基本性質。

引理1.1[12]設L是完備剩余格,則?a,b,c∈L,下列式子成立：

(Ⅰ1) 0*a=0且1→a=a,

(Ⅰ2)a≤b?a→b=1,

(Ⅰ3) (a→b)*(b→c)≤a→c,

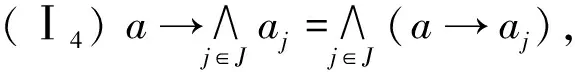
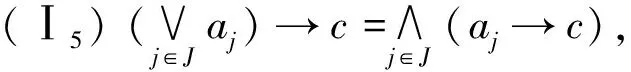
(Ⅰ6)a→(b→c)=b→(a→c)=a*b→c,

(Ⅰ7)a*(a→b)≤b。

設X為一非空集合，X上的模糊子集就是從X到L上的映射，X上的所有模糊子集記為LX。?A,B∈LX,A和B之間的相等可以通過一般映射之間的相等來定義，也就是說，A=B??x∈X,A(x)=B(x)。

定義1.1[5]X上的模糊關系e是X×X上的模糊子集，即e:X×X→L。X上的模糊關系e稱為是模糊偏序，若e還滿足：

(1) ?x∈X,e(x,x)=1;

(2) ?x,y,z∈X,e(x,y)*e(y,z)≤e(x,z);

(3) ?x,y∈X,e(x,y)=e(y,x)=1?x=y。

稱(X,e)為模糊偏序集，若e是X上的模糊偏序。A∈LX稱為模糊上集，若?x,y∈X,A(x)*e(x,y)≤A(y)。A∈LX稱為模糊下集，若A(x)*e(y,x)≤A(y)。記L(X)為X上所有模糊下集。

定義1.2[6,9]設(X,e)是模糊偏序集，x0∈X稱為模糊子集A的并，記為x0=凵A， 若滿足下列條件：

(1) ?x∈X,A(x)≤e(x,x0);

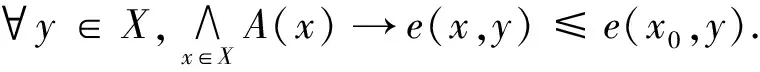
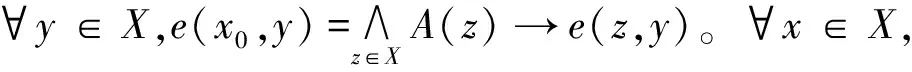
在引理1.2中，若A=↓x,則

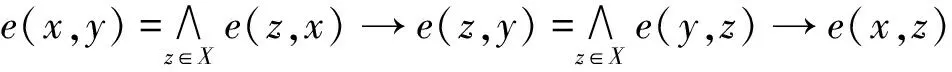
定義1.3[6-7]稱模糊偏序集(X,e)為模糊完備格，若它滿足?A∈LX,凵A存在。

例題(1) ?x,y∈L,定義eL:L×L→L如下：eL(x,y)=x→y,則eL不僅是L上的模糊偏序，還可以證明它是(X,e)上的模糊完備格。

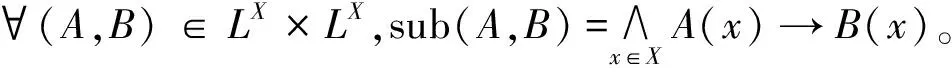
定義1.4[5,8]設(X,eX)、(Y,eY)為模糊完備格，稱映射f:(X,eX)→(Y,eY)為模糊單調的，若?x,y∈X,eX(x,y)≤eY(f(x),f(y))。顯然，模糊映射凵是模糊單調的。

定義1.5[9]設(X,e)是模糊完備格。?x,y∈X,:X×X:→L定義如下：

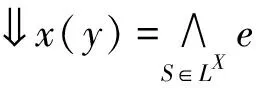
定義1.6[7]模糊完備格(X,e)稱為模糊完全分配格，若它滿足：?x∈X,x=凵x。

引理1.3[6-9]設(X,e)是模糊完備格。則?x,y,u,v∈X,下列式子成立：

(2)e(u,x)*y(x)*e(y,v)≤v(u).

引理1.4[8-9]在模糊完備格(X,e)中，模糊well-below關系具有插入性質，即

2 模糊Cut集

這部分主要給出模糊Cut集的概念，證明所有的模糊Cut集可構成模糊完全分配格。

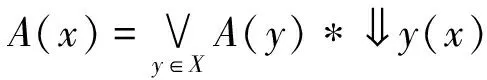
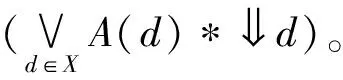
證明?y∈X,有

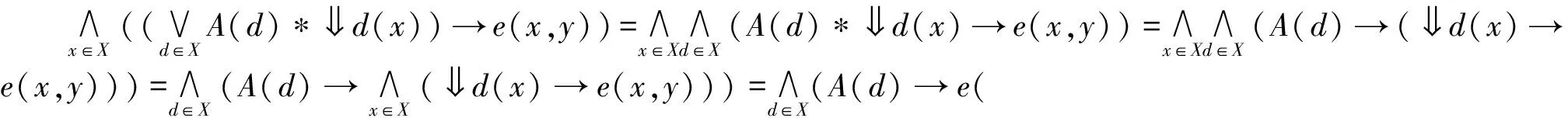
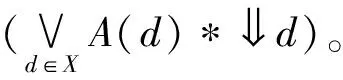
引理2.2若(X,e)是模糊完全分配格，則?A∈LX,凵

證明一方面，?x∈X,

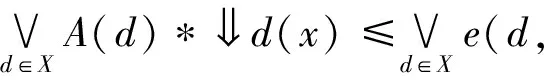
另一方面，由引理2.1，可得

定理2.1若(X,e)是模糊完全分配格，則C(X)={x|x∈X}。

證明顯然，?x∈X,x是模糊下集。根據引理從而x∈C(X)。

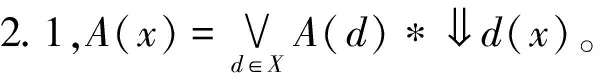
引理2.3在模糊完備格(X,e)中，?x,y∈X,x(y)≤sub(y,x)。

證明顯然成立。

引理2.4在模糊完全分配格(X,e)中，?x∈X,G∈LL(C(X)),(凵G)(x)≤G(x)。

證明因為(X,e)是模糊完全分配格，根據定理2.1和引理2.3，

為得到主要結論，下面介紹模糊極小集。

定義2.2設(X,e)為模糊完備格。?x∈X,稱模糊子集β∈LX為x的模糊極小集，若它滿足x=凵β和β≤x。

命題2.1設(X,e)是模糊完備格。?x∈X,若在x處存在模糊極小集，則x最大。

證明假設β是x處的模糊極小集，根據定義2.2，x=凵β且β≤x,而1=sub(β,x)≤e(凵β,凵x)=e(x,凵x)。同時，e(凵x,x)=1。從而x=凵x,顯然有x≤x。因此，x是點x處的模糊極小集。顯然它是最大的模糊極小集。

根據上面的命題，可得到下面的結論。

命題2.2模糊完備格(X,e)是模糊完全分配格當且僅當?x∈X,在x處有模糊極小集存在。

下面給出模糊極小集的等價刻畫。

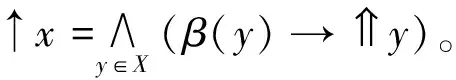
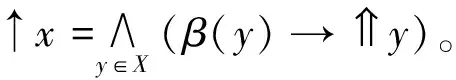
一方面，?y,z∈X,

e(x,z)*β(y)≤e(x,z)*x(y)≤z(y)=y(z)

故e(x,z)≤β(y)→y(z)。由于y和z的任意性，有

另一方面，

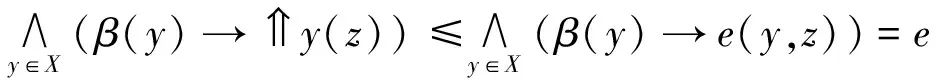
充分性。只需證β≤x。因為故

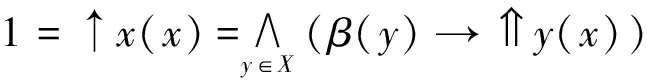
從而?y∈X,β(y)≤y(x)=x(y)。 所以β≤x。

綜合命題2.2和命題2.3的內容，可得到下列結論。

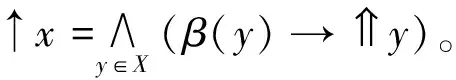
基于模糊極小集，下證所有的模糊C(X)集可構成模糊完全分配格。為此，先證它是模糊完備格。

定理2.3若(X,e)是模糊完全分配格，則(C(X),sub)是模糊完備格。

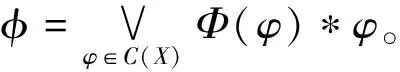
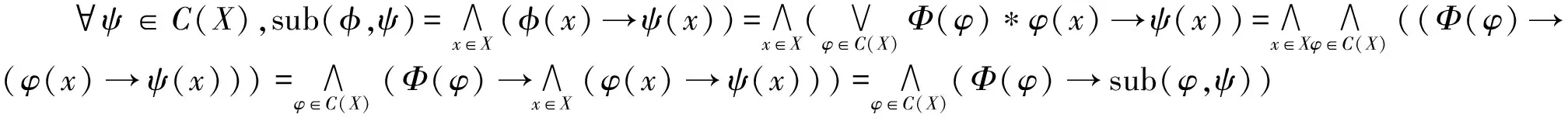
故凵Φ=φ。此外，?x,y∈X,

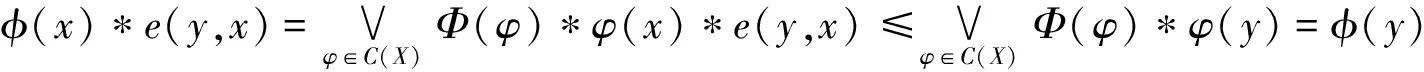
因此，φ是模糊下集。根據定理2.1及插入性質，

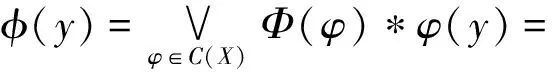
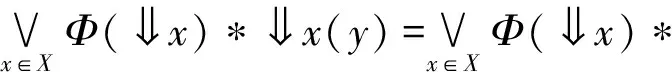
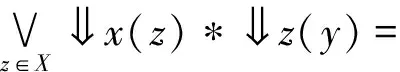
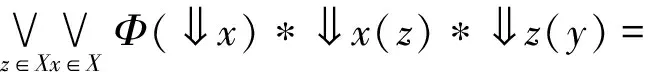
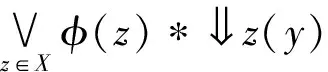
因此，(C(X),sub)是模糊完備格。

定理2.4若(X,e)是模糊完全分配格，則(C(X),sub)是模糊完全分配格。

證明由定理2.1，?φ∈C(X),?x∈X,滿足φ=x。定義Φ:C(X)→L如下：下證凵Φ=x和Φ(-)≤(x)(-)。?ψ∈C(X),有

故凵Φ=x。

此外，?y∈X,φ∈C(X)和G∈LL(C(X)),根據引理2.4，

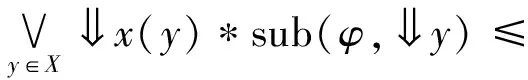
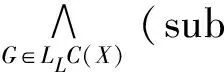
從而Φ(φ)≤(x)(φ)。由命題2.2和定理2.3可知，(C(X),sub)是模糊完全分配格。