鋰離子電池正極材料中的極化子現象理論計算研究進展

葉耀坤，胡宗祥，劉佳華，林偉成，陳濤文，鄭家新，潘鋒

北京大學深圳研究生院新材料學院，廣東 深圳 518055

1 引言

鋰離子電池具有能量密度高、壽命長、無記憶效應、無污染產物等優點，目前已在智能手機、移動電源、筆記本電腦、電動汽車等領域得到廣泛應用1,2。然而，鋰離子電池的性能仍有待進一步改善和提高。例如，特斯拉等品牌電動汽車頻繁報導的自燃事件引發了人們關于鋰離子電池安全性的擔心。隨著電子設備的日益多樣化和電動汽車的日益普及化，人們對于高性能(如能量密度高、充放電速度快、安全性能好等)鋰離子電池的需求日益增長。為改善和提高鋰離子電池的電化學性能，研究學者分別從正極材料、負極材料、電解液、隔膜等角度入手，開展了大量科學研究3–5。

正極材料是鋰離子電池最為重要的組成部分，其結構類型多樣，最典型的是以LiCoO2為代表的層狀結構、以LiFePO4為代表的橄欖石結構和以LiMn2O4為代表的尖晶石結構，如圖1所示。盡管它們因自己獨特的優點已經在商業化上取得了成功，但都還存在顯著的不足。LiCoO2理論容量高、導電性能好；但由于其在完全脫鋰所需要的高電壓下呈現出的結構不穩定性，其實際容量大約只能達到理論容量的一半6，且鈷價格昂貴、具有毒性。LiFePO4具有良好的結構穩定性和安全性；但其電子導電性能差，長期以來人們需要采用碳包覆和納米化等策略來提高其導電性能7–9。LiMn2O4具有價格低、安全性能好等優點；但它在循環過程中由于存在高自旋3d4的Mn3+，會引發Jahn-Teller畸變，進而產生結構相變和容量快速衰減；與此同時，Mn3+會發生歧化反應生成Mn2+和Mn4+，導致LiMn2O4容易在充放電過程中溶解到電解液中10–12。

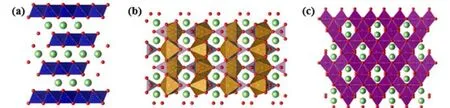
圖1 (a)以LiCoO2為代表的層狀正極材料；(b)以LiFePO4為代表的橄欖石型正極材料；(c)以LiMn2O4為代表的尖晶石型正極材料Fig. 1 (a)Layered cathode materials represented by LiCoO2; (b)Olivine cathode materials represented by LiFePO4;(c)Spinel cathode materials represented by LiMn2O4.

鋰離子電池的充放電速率直接由其倍率性能這一核心參數反映，它與正極材料的電子導電率有著密切關系，而電子導電率會受到正極材料中能量分布和空間分布的影響。如果電子在空間上傾向于局域分布，進一步與晶格耦合形成極化子，將會對導電性產生不利影響，例如含有極化子的LiFePO4室溫下電子導電率僅有10-9S·cm-1。所以基于人們對鋰離子電池充放電速率的追求，正極材料中的極化子現象的研究日益受到人們的關注13–19。研究極化子可分別從實驗和理論計算兩方面進行，但近年來，隨著理論計算方法的發展，人們逐漸改變了傳統電池開發中“Trial and Error”的試錯模式，采用實驗和理論研究相結合的方法進行了大量的機理探索研究，加速了研發進程20,21。基于極化子在正極材料中的廣泛出現和其對于電子導電性的重要研究價值，本文將主要從理論計算的角度出發，首先介紹極化子的基本物理概念，其次對極化子的理論計算判別方法、極化子對常見類型正極材料導電性能的影響與調控和當前研究方法的一些理論難題進行綜述，最后分別從基礎理論和實際應用兩個方面展望未來對于正極材料中極化子的研究。這篇綜述將為研究者從理論計算角度理解鋰離子電池正極材料中的極化子現象以及未來設計高電子導電性正極材料提供重要參考。

2 極化子現象的相關理論簡介

理想晶體的主要特征是晶格原子排列具有嚴格的周期性，但實際晶體中的原子排列總是會偏離理想位點，從而破壞晶體的嚴格周期性，是一種強電聲耦合導致的晶格畸變密切相關的晶體點缺陷22。由于運動電子自身的庫倫勢，運動電子會吸引正離子、排斥負離子，從而產生使周圍晶格極化的相對位移，形成一個圍繞該運動電子的極化場。極化場會反作用于電子，改變電子的能量和運動狀態并束縛該電子，阻止其從這個區域逃逸出去，這種束縛作用稱為“自陷(self-trapped)作用”。在自陷作用下，晶格畸變會伴隨電子運動，構成一個相互作用的整體，稱為極化子23。同時，在晶格伴隨電子的遷移過程中，電子需要拖著附近“笨重”的晶格共同行走，導致載流子的有效質量變大，進而導致其遷移率變得很低。

極化子可以根據周圍晶格畸變區域的大小和晶格常數的比較分為大極化子和小極化子：當畸變區域比晶格常數數量級大得多時稱為大極化子，當畸變區域小于晶格常數數量級或與晶格常數數量級相當時，稱為小極化子，如圖2所示24。極化子是具有遷移能力的準粒子，其動力學模型通常由極化子跳躍(polaron hopping)來描述。Deskins等25詳細論證了基于Marcus電荷轉移理論和Emin-Holstein-Austin-Mott (EHAM)極化子運動理論的極化子跳躍模型；以TiO2為例，其電荷轉移過程可以用圖3形象表示。表126羅列了小極化子和大極化子的對比差異，基于這些特性，對于包含我們研究關心的鋰離子電池正極材料在內的過渡金屬氧化物體系，通常認為載流子能形成的都是小極化子13，故本文后續的“極化子”一詞均代指小極化子。簡言之，極化子是一種晶格畸變束縛電子作整體運動的晶體缺陷。

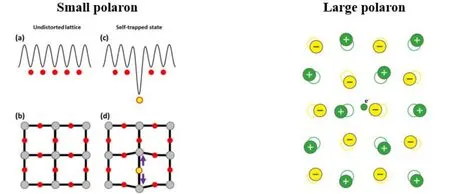
圖2 小極化子(左)和大極化子(右)示意圖24Fig. 2 Schematic diagram of small polaron (left)and large polaron (right)24.

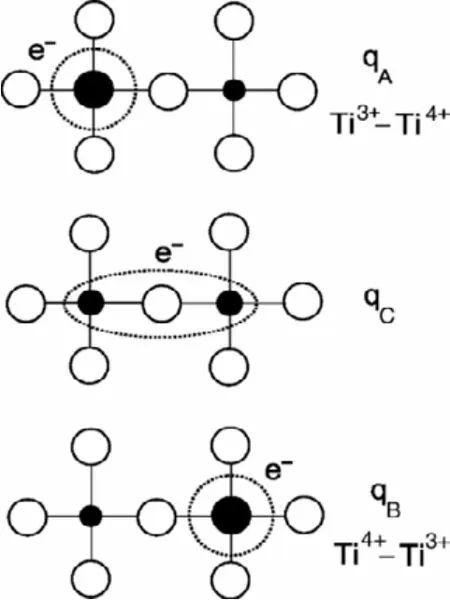
圖3 極化子電荷轉移示意圖25Fig. 3 Schematic diagram of polaron e- transfer 25.

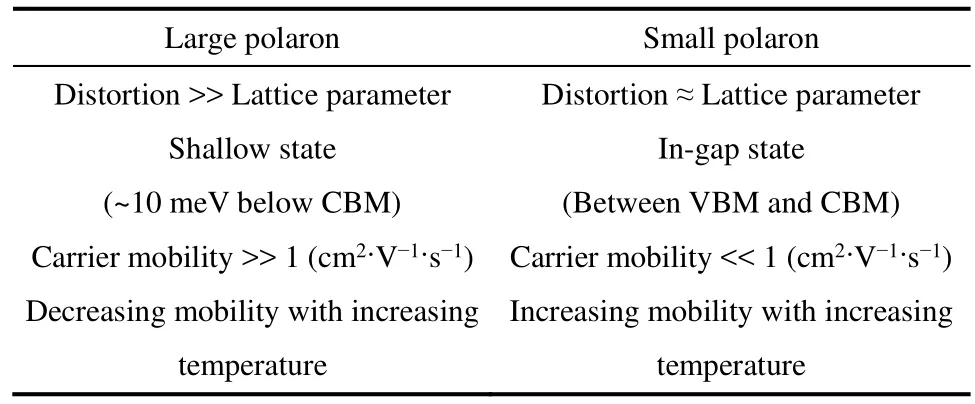
表1 大極化子和小極化子常見性質對比26Table 1 A comparison of general properties of large polaron and small polaron 26.

3 極化子的判別方法

3.1 理論判別方法

隨著第一性原理計算方法的發展，我們可以僅從理論上給出極化子現象是否出現的判據，從而將其結果用于實驗現象的機理解釋，或者用于一些實驗未知體系的理論預測。

3.1.1 通過能態密度圖判斷

能態密度(Density of States，DOS)是固體能帶理論的重要指標，它反映了體系電子隨能量的分布。鋰離子電池在工作時，鋰離子會在正負極之間反復脫嵌，計算并對比正極材料不同鋰含量下的DOS圖，可以很好地模擬對應正極材料工作時的電子結構變化，幫助我們理解其背后的物理化學過程。根據極化子定義，晶格畸變形成的極化場會束縛體系內的某個電子，改變其能量與運動狀態，形成一種位于價帶頂(VBM)和導帶底(CBM)之間的類雜質態(In-gap state)26，對應DOS圖中會展現一個類雜質態的特征峰。Zheng等15使用Lany-Zunger方法(Lany-Zunger Approach)27，通過DOS圖中的特征峰，結合自旋電荷密度圖展示的可視化局域電荷，計算模擬了Li2FeSiO4材料的脫鋰中間態LiFeSiO4在微量鋰離子脫嵌時的電子結構變化，判斷了該體系中存在極化子，如圖4所示。

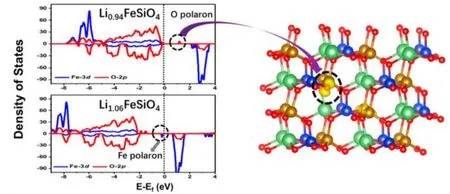
圖4 通過DOS圖理論判斷Li2FeSiO4極化子15Fig. 4 Theoretical observation of polaron in Li2FeSiO4 using DOS 15.

下面再以LiCoO2和LiFePO4為例簡要說明如何通過DOS圖中的極化子態來理解極化子對鋰離子電池性能的影響。在滿鋰狀態時，LiCoO2和LiFePO4都是不導電的半導體，當脫去少量鋰后，LiCoO2會呈現金屬性質，而LiFePO4則是會出現極化子態。用圖5所示的DOS圖的語言表述，當體系為Li1-xCoO2和Li1-xFePO4時，Li1-xCoO2會呈現出能態穿越費米能級的導體性質，而Li1-xFePO4則呈現出帶有極化子態的半導體性質，這就從固體能帶理論的角度解釋了為什么極化子會減弱體系的電子導電性28。

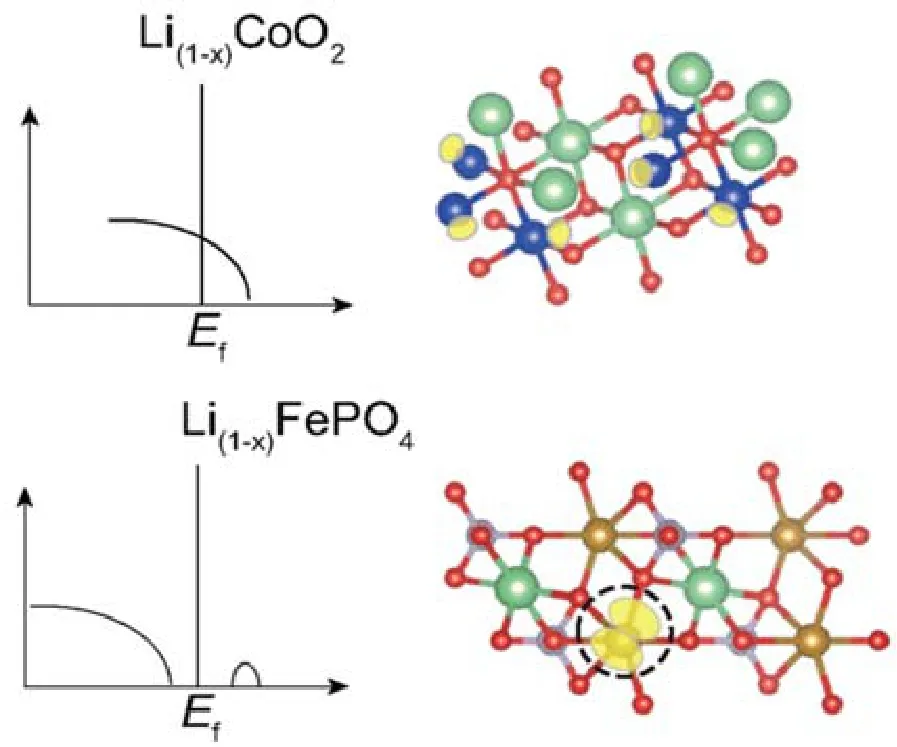
圖5 極化子態對導電性能影響的固體能帶理論解釋示意圖28Fig. 5 Schematic diagram of polaron’s impact on conductivity according to band theory 28.

3.1.2 通過原子磁矩的變化判斷

鋰離子電池正極材料通常含有過渡金屬元素(如Ni、Co、Mn等)，這些過渡金屬元素原子可能含有未配對的自旋電子，而這些未配對的自旋電子會生成屬于該原子的凈磁矩，通過原子與原子之間凈磁矩的排布，材料體系可以進一步分為鐵磁性、反鐵磁性和無磁性等。鋰離子電池正極材料正常工作時會不斷脫嵌鋰離子，由于體系Li含量的變化，體系要想維持原有的整體電中性，就要有其他原子參與得失電子，根據不同元素之間的電負性關系，此時電子的得失通常是來自體系含有的過渡金屬，電子的得失對應著過渡金屬原子的變價行為。當體系不存在極化子時，體系內的電荷相對呈整體分布，體系內的過渡金屬原子會整體均勻變價；當有極化子存在時，由于體系內的某個電荷會被晶格畸變束縛，呈現出很強的局域性，體系內的過渡金屬原子整體均勻變價行為被破壞，會呈現出局域電子優先變價。電子的得失會反映在過渡金屬原子的磁矩上，因此我們可以通過磁矩變化來描述體系的變價行為。當極化子現象出現時，會觀察到某一過渡金屬原子磁矩的單一變化，而不是體系所有過渡金屬原子磁矩的整體變化，這也是判斷極化子現象出現的一個重要根據。以LiFePO4單胞體系(共計28個原子，其中4個Li原子、4個Fe原子、4個P原子、16個O原子)為例，在其脫鋰過程中，體系由LiFePO4轉變為LixFePO4(x=1, 0.75, 0.5, 0.25, 0)。由于體系Li含量的降低，需要Fe參與得失電子來維持體系的整體電中性。如圖6所示16，當LiFePO4單胞的4個Li依次脫去時，其Fe的磁矩會依次獨立變化，而非整體平均變化，是典型的極化子磁矩變化現象。

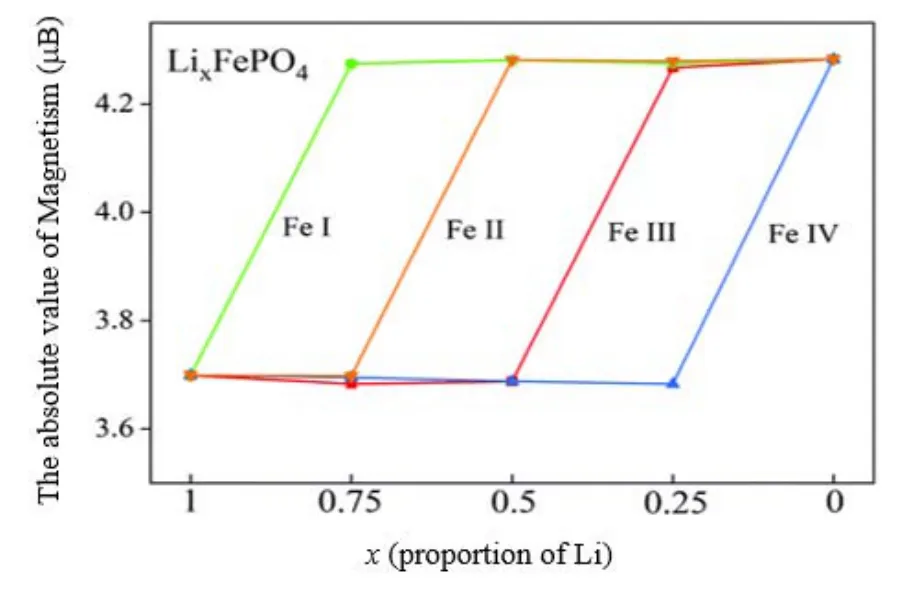
圖6 通過原子磁矩變化理論判斷LiFePO4極化子現象16Fig. 6 Theoretical observation of polaron in LiFePO4 according to the change of magnetic moment 16.

在LiO2中電子和空穴會局域到氧二聚體上形成極化子。在LiO2超胞中人為地引入了一個電子或空穴(后者對應于體系減少一個電子)，結構優化后有兩種情況出現：一種對應了離域態的電子或空穴，另一種則是局域態的極化子。在出現了離域態電子或空穴的超胞中，對稱性仍然維持在未增加或減少電子時的狀態，所有的氧二聚體同等地分享了超胞中引入的電子或空穴。而在局域態的情況中，超胞的對稱性被破壞，其中一個氧二聚體的磁矩將發生明顯變化。“氧氣分子”的軌道排布我們已經非常熟悉了，其分子的成鍵軌道為6個電子占據的和剩余2電子占據的反鍵軌道為由于兩個反鍵軌道上有兩個沒配對的電子，因而具有2μB的總自旋磁矩。在圖7中我們能看到氧氣分子的電子排布示意圖和自旋密度分布圖。而超氧根離子是反鍵軌道π*又多占據了一個電子形成的離子分子。對比氧氣分子的電子排布，我們可以看到，超氧根離子反鍵軌道π*上多占據的電子與原來的電子成對，呈自旋反平行排布，因而超氧根離子具有1μB的總自旋磁矩。從磁矩密度圖上，我們也能看出磁矩密度相對于氧氣分子減小了。空穴極化子就是超氧根離子失去一個電子成為離子的反鍵軌道仍可以再占據一個電子形成過氧根離子，從圖7中我們可以看到由于電子全部成對而沒有磁矩密度的過氧根離子，這在LiO2系統中也就是電子極化子29。

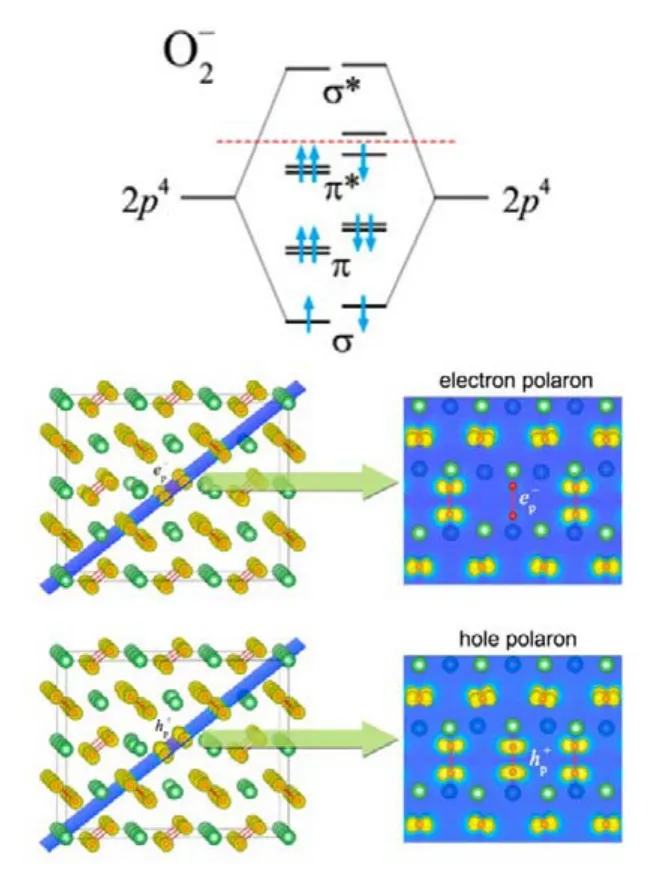
圖7 極化子在自旋密度分布圖上的反映29Fig. 7 Theoretical observation of polaron according to spin density 29.

3.1.3 通過結構局域畸變判斷

與磁矩變化類似，出現極化子時，除被束縛電荷呈現出很強的局域性外，束縛電子的畸變晶格也呈現出畸變的局域性。以理論和實驗都觀測到極化子的Li2FeSiO4材料為例，當體系未脫鋰時，Si―O四面體的鍵長相對均一，O―O鍵長在2.7 ?(1 ? = 0.1 nm)左右，Si―O鍵長在1.63 ?左右，當體系脫鋰后，極化子出現，鍵長變化不均勻，出現有一個O―O鍵變為2.34 ?而其余O―O鍵變化較小的現象，如圖8所示，因此通常也將這種局域畸變用來作為出現極化子現象的一個判據15。Wang等30高通量計算了層狀材料和尖晶石材料脫鋰前后的體積變化率，發現含有極化子的LiMnO2體系的體積變化率(3.78%)和LiMn2O4體系的體積變化率(5.67%)均處在同等材料的中部區間(層狀材料體積變化率區間為0.04%–13.1%，尖晶石材料為0.41%–13.27%)。此外，LiFePO4同時存在著良好的結構穩定性和顯著的極化子現象，即使考慮到磷酸根基團對其結構穩定性的貢獻，也很難忽視其結構穩定性和極化子現象之間的關聯。盡管尚未定論，但相較于沒有極化子時的整體畸變，極化子引起的局域畸變在理論上造成的體積變化會相對有所減弱，從而在一定程度上增強了體系的結構穩定性。

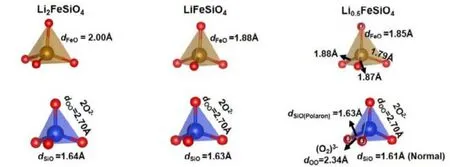
圖8 極化子引發的局部畸變示意圖15Fig. 8 Schematic diagram of local distortion induced by polaron 15.

在LiO2體系中，極化子對晶格的影響直接表現為O―O鍵長的變化。在引入電子的情況中，一個離子變為，其O―O鍵長從原來的1.30 ?增加到1.44 ?。而在引入空穴的情況中，一個離子變為，其O―O鍵長減少到1.19 ?。這從之前的LiO2中O原子的態密度可以知道，中最高的被占據軌道是反鍵軌道π*。增加一個電子時，該電子會進入到π*軌道上，從而導致O―O鍵的強度被削弱，因此出現了O―O鍵長明顯增加的現象。而引入一個空穴時，該空穴也同樣位于π*軌道上。反鍵軌道上電子的減少使得O―O的鍵強度被加強，因而表現為O―O鍵長明顯變短，如圖9所示29。

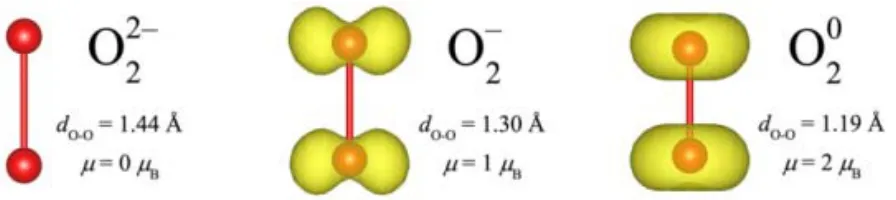
圖9 極化子現象引發的鍵長變化示意圖29Fig. 9 Change of bond length induced by polaron 29.

盡管以上列舉的這些條件都是判斷極化子的重要論據，結合這些判據是當前判斷極化子較為準確的方法，但遺憾的是，目前我們的確尚未發現有一條普適的充分必要條件能用來判斷說明極化子的存在。以局部畸變為例，雖然極化子的出現會伴隨著局部畸變的產生，但僅從局部畸變出發顯然無法得出體系含有極化子這一結論，一個典型的例子就是Jahn-Teller效應。八面體配位場的過渡金屬原子3d軌道會劈裂為二重簡并的eg軌道和三重簡并的t2g軌道，如果此時eg軌道上有未成對的單電子，則體系會進一步退簡并，在退簡并過程中降低體系能量，誘發Jahn-Teller畸變，從而使得體系能夠穩定下來。Jahn-Teller效應分為靜態和動態效應。對于靜態Jahn-Teller效應，結構變形會降低系統的對稱性并消除能級的簡并。對于部分填充的能級，這種結構變形因此會導致系統總能量的降低，因為多重簡并的低能態被占據而高能態仍然是空的，能級會發生重排消除這種不穩定的簡并狀態，當體系有不止一種可能導致對稱性降低的形變時將發生動態Jahn-Teller效應。在Zuo等31最近的工作中，他們發現普通尖晶石錳酸鋰中的過渡金屬錳離子有一半為三價陽離子，具有Jahn-Teller效應活性，其錳離子eg軌道如圖10a左圖所示：eg兩個軌道一個被占據，一個沒有被占據，能級發生劈裂。而引入陽離子無序性(Mn位上過量的Li和Li/Mn交換)可以固有地抑制MnO6八面體的協同Jahn-Teller畸變(CJTD)并抑制Mn3+歧化。圖10a右圖為引入無序消除JT效應后，三價錳離子的eg軌道的分布。陽離子無序可破壞Mn3+排列的對稱性，從而破壞由各個Jahn-Teller中心引起的畸變的相關性，并防止Mn―O鍵沿同一個方向扭曲，形成局部畸變，結構變化如圖10b所示。但這樣的局部畸變對應的不是極化子現象，因此對極化子不能僅根據某一判據單一判斷，而是需要根據以上判據進行綜合判斷。當然，正如Reticcioli等26建議的那樣，極化子的理論計算和實驗的對比仍然是非常有必要的(“Ultimately, comparison with the experiment,however, remains necessary and mandatory”)。我們下面將簡要介紹極化子的實驗判別方法。

2) 三級數量彈性契約的供應鏈在價格隨機或是價格穩定的突發事件下顯現出來的規律性質大體相同.它們的主要區別是：價格隨機情景下批發價調整的幅度、供應鏈上企業的期望收益變化的比率，要比價格穩定的情況要大一些.由此可見，價格隨機的突發事件對供應鏈系統的影響較大，企業需要采取定特定的手段以消除突發事件的影響.

圖10 尖晶石錳酸鋰中的Jahn-Teller效應31Fig. 10 Jahn-Teller effect in the spinel LiMn2O4 31.

3.2 實驗判別方法

理論計算預測了極化子在材料體系中的存在，可以通過實驗手段來加以驗證。X射線吸收光譜(XAS)，X射線發射光譜(XES)，共振非彈性X射線散射(RIXS)和X射線光電子能譜(XPS)等檢測技術都是實驗用來表征材料電子結構、能帶信息的常用手段。但是，材料樣本中已經具有明顯扭曲的局部環境，因此小極化子(弱的局部畸變)及其光譜指紋非常容易受到core-hole效應的影響，這使得它很難可以通過XAS或非諧振XES進行簡單檢測。由于core-hole效應在X射線光電子能譜較小，因此極化子的半經驗信號可以通過XPS的手段來得到驗證。此外，掃描隧道顯微鏡與光譜學(Scanning Tunneling Microscopy and Spectroscopy)32、紅外吸收光譜(Infrared Spectroscopy)33和電子順磁共振(Electron Paramagnetic Resonance)等34也是實驗上觀測極化子的重要手段。在最新的研究中，Guo等35使用脈沖激光結合的掃描隧道顯微鏡與光譜學技術(Pulsed-Laser-combined Scanning Tunneling Microscopy and Spectroscopy)，成功在光催化材料金紅石相TiO2的(110)面發現極化子，如圖11所示。

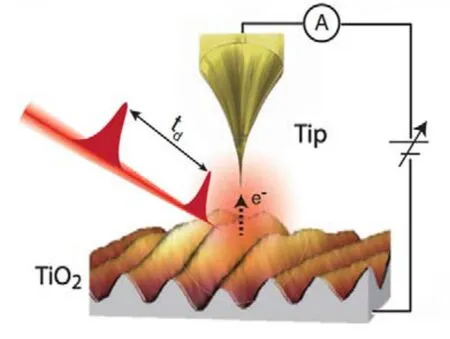
圖11 Laser-combined STM探測極化子態35Fig. 11 Polaron state observed by Laser-combined STM 35.

4 極化子在常見類型正極材料中的研究與調控

極化子現象在鋰離子電池正極材料的研究中已引起越來越多的關注，本節對層狀、橄欖石和尖晶石三種常見正極材料中的極化子的研究與調控進行綜述。

4.1 層狀(Layered)材料

隨著LiCoO2最早的商業化成功，層狀材料一直以來是備受關注的正極材料類型。在LiCoO2早期研究中，Marianetti等36發現LiCoO2在脫鋰過程中極易發生莫特相變，其半導體性質對應轉變為導體性質，這能很好解釋LiCoO2良好的導電性。他們認為像LiCoO2這樣的層狀材料中電聲耦合作用較弱，不易形成極化子，這一猜想被后續實驗證實。Dahéron等37制備并觀測了從LiCoO2到CoO2的脫鋰過程，通過X射線光電子能譜的實驗手段得到了LiCoO2脫鋰過程中存在強烈的電子離域態這一重要結論，與需要局域化電子才能形成的極化子形成鮮明反差，從理論上排除了LiCoO2中存在極化子的可能性。然而，盡管有著相似的結構，不同層狀材料之間的電子導電性卻有著顯著差異。室溫條件下，LiCoO2和LiNiO2的電子導電率分別為10-3到10-2S·cm-1和10-1到100S·cm-1量級 ， 而LiMnO2卻只有10-5到10-3S·cm-1，Li2MnO3甚至只有10-9S·cm-1量級38，Kong等14通過理論計算在層狀LiMnO2和Li2MnO3中確認了極化子的存在，解釋了這一電子導電率的差異，再次論證了極化子對于正極材料導電性能的極大影響。他們嘗試了Mg、Ti、V等10種陽離子和N、F兩種陰離子摻雜，將LiMnO2和Li2MnO3的導電性能分別提升了106和2 × 104量級。Feng等19在實驗上合成了層狀三元組分材料LiNi0.4+xMn0.4-xCo0.2O2(x= 0, 0.1, 0.2, 0.3)，并發現在升溫(293.15–573.15 K)和Ni組分提高時體系的電子導電率都有著顯著提升，如圖12所示。他們指出電子導電率升高的原因是體系內的極化子得到了離域化，揭示了極化子與正極材料導電性能之間的關系。

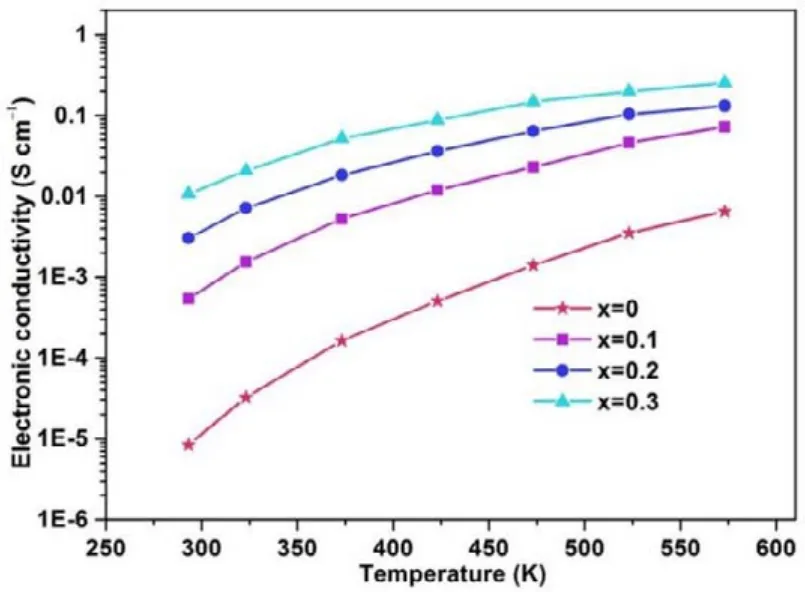
圖12 LiNi0.4+xMn0.4-xCo0.2O2的電子導電率變化圖19Fig. 12 Changes of electronic conductivity of LiNi0.4+xMn0.4-xCo0.2O2 19.

4.2 橄欖石(Olivine)型材料

橄欖石型正極材料也被稱為聚陰離子型正極材料，這類材料的優點是地球儲量豐富、環境友好、成本便宜且結構穩定、安全性能好，自Goodenough和Padhi等人最早提出將LiFePO4用于做鋰離子電池的正極材料以來，橄欖石型材料被廣泛關注與研究39。LiFePO4有著導電性差的嚴重缺點，其帶隙寬度大約在3.7 eV附近，室溫下的電子導電率僅有10-9S·cm-1量級40。盡管人們可以通過碳包覆和減小粒徑等途徑提高其導電率，但這些方法未觸及到其本質問題。基于該類型材料的諸多優點，理解其電子結構對鋰離子電池的實際應用具有非常重要的作用。如圖13所示，Ouyang等41計算了LiFePO4中Li的遷移，他們通過分析對比不同的遷移路徑，指出只有當鋰離子沿c軸擴散時其能壘才會很低(0.6 eV)，從理論上揭示了LiFePO4中鋰離子呈一維通道擴散，并通過第一性原理分子動力學模擬觀測到了一維擴散這一行為。Ceder等13提出，當LiFePO4中存在過多的電荷載流子時，其環境中的原子被極化并移位，從而產生局部晶格畸變。載流子通過局限在這種晶格變形中而降低了能量并變得自陷，通過第一性原理計算發現LiFePO4中的導電機理是極化子跳躍，其極化子的遷移能壘約為200 meV。隨后關于LiMPO4(M = Fe, Mn, Co, Ni)的極化子研究的理論和實驗工作被相繼報導18,42，Gu等16在此基礎上使用HSE雜化泛函的理論計算結果表明，如果在Li位點直接替換同主族元素Na，由于其不能改變脫鋰過程中Fe的極化子行為，對電子導電率并沒有顯著提升；在Fe位點摻雜Mn和Co仍有極化子出現，但Fe位置摻雜Ni會發現極化子行為接近消失，導致這一差異的原因可能是Ni―O鍵具有更強的共價性質。為提高橄欖石型正極材料的導電性能，Chung等43在實驗上使用Mg、Al、Ti等異價離子摻雜可以將其電子導電率提升108量級。Li等40在理論計算的先行指導下，在實驗上制備了使用Cr摻雜的Li0.97Cr0.01FePO4和Li0.91Cr0.03FePO4，它們的電子導電率在室溫下與純LiFePO4相比有明顯提升。

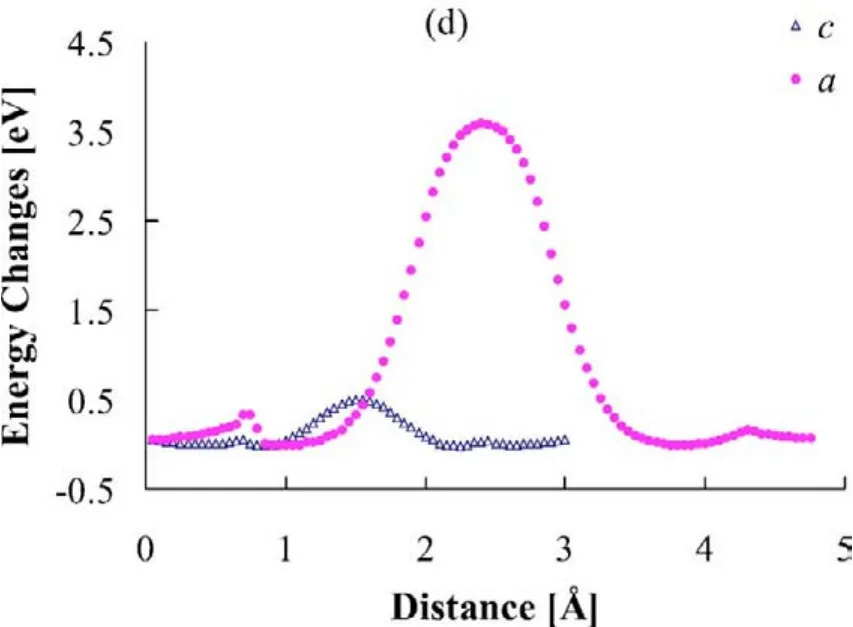
圖13 LiFePO4沿a軸和c軸擴散能壘對比圖41Fig. 13 A comparison of the energy barriers along a andc directions in LiFePO4 41.

4.3 尖晶石(Spinel)型材料

1983年，Goodenough提出可以將尖晶石錳酸鋰(LiMn2O4)作為正極材料，LiMn2O4具有價格低、安全性能好等優點，至今仍受到學界和產業界的高度關注44。與LiFePO4材料不同的是，人們在早期研究中就認識到了LiMn2O4中存在極化子躍遷45–47，其電子導電率大約在10-6S·cm-138。Ouyang等48詳細計算了λ-MnO2、Li0.5Mn2O4和LiMn2O4的極化子遷移能壘，總結出其遷移能壘的大小與Mn的3dz2軌道受Jahn-Teller畸變后的能級偏移程度有著密切聯系。Rojo等49,50通過嘗試摻雜Co、Ni等元素，從實驗上提升了LiMn2O4的電子導電率。

綜上，極化子現象對正極材料最為重要的影響是嚴重降低了其導電性能，從而極大限制了正極材料的應用。因此，通過調控極化子來提高正極材料的電子導電率，成為了設計高導電性正極材料的一個重要途徑。當前極化子的調控策略，主要還是以摻雜為主，合理的摻雜手段可以減弱極化子的影響，顯著提高材料的電子導電率。

5 理論計算的研究困難及其改進方法

盡管理論計算方法在研究極化子方面已經取得了很大成功，然而傳統理論方法在研究極化子時會面臨一些由于方法自身缺點所導致的困難，本節對其進行簡要介紹，并說明針對這些困難采用的改進方案。

5.1 局域最小值(Local Minimum)問題

局域最小值問題包含兩類情況，分別是原子結構弛豫優化的局域最小值問題和原子磁矩的局域最小值問題。我們在進行理論計算研究時，最為重要的步驟之一是需要找到研究體系的基態(能量最低、熱力學最穩定的狀態)，從而保障后續計算結果的可靠性，這對于極化子這類原子結構和電子結構都有著高精度要求的研究來說尤為重要，但局域最小值問題的存在嚴重妨礙了體系基態的尋找。與局域最小值這一概念相對應的是全局最小值(Global Minimum)，理論上說，我們期望找到的基態應該是研究體系所有可能狀態的全局最小值(如圖14中的b點)。然而，全局最小值的尋找問題在當前計算機算法領域都仍是一個有待解決的前沿研究問題；即使全局最小值可以實現，它的計算量對于計算資源的需求也會急劇增長，可能會大幅增加理論計算的負擔。基于此，我們在研究極化子現象時，需要正視局域最小值問題，通過盡可能多地嘗試原子結構排布和原子磁矩排布，并從得到的一系列“局域最小值”結果中篩選出一個能量最低的、最有可能的排布，使得我們得到的局域最小值結果盡可能地近似于全局最小值結果，將誤差控制在現有理論計算方法的可接受范圍內，是當前理論計算研究中，在計算資源消耗處于較為接受的情況下，最具可行性的操作方案。

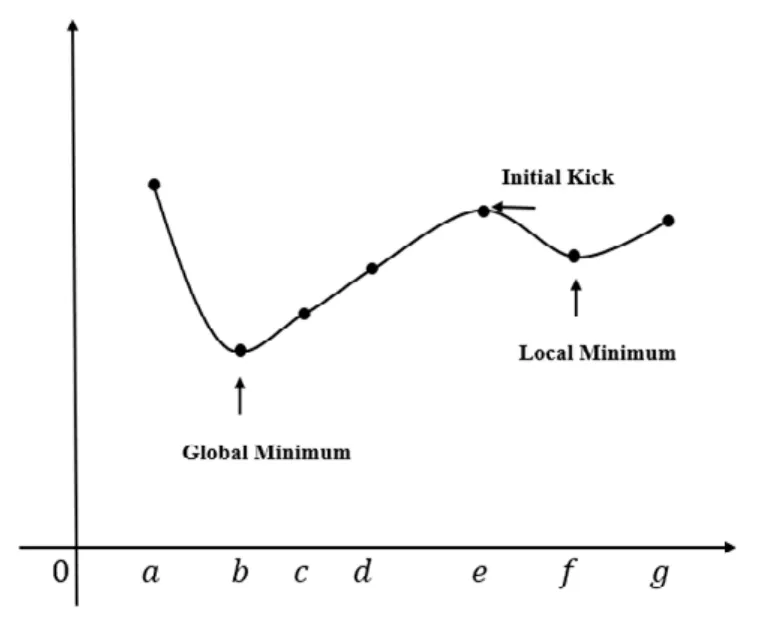
圖14 局域最小值和全局最小值示意圖Fig. 14 Schematic diagram of local minimum and global minimum.

用圖14來描述，如果我們不對排布進行盡可能多的嘗試，那么我們可能僅得到局域最小值的f點，從而得出了錯誤的結論(因為真正的最小值點是b點)；而當我們嘗試盡量多的排布時，我們可能會得到包含b點和f點在內的系列最小值點，通過這些最小值點之間的比較從而得出正確的結果。此外，通過給予位于初始平衡位置的原子一個偏離平衡位置的初始位移(Initial Kick)，從而可以減少遇到原子位于鞍點而滑落到呈現局域最小值的亞穩態的概率，也是在極化子計算中常用的研究方法14,26。以空穴極化子為例，二氧化鈦51、過氧化物52和鋰硫53等材料中的價帶空穴往往會被困在帶負電荷的受體缺陷上，形成空穴極化子。BiVO454、LiFePO455等含過渡金屬的材料，由于過渡金屬與配位的氧離子會發生強烈的共價作用，空穴極化子也會局域在陰離子氧上。這類體系在實際計算操作中通過從晶格體系中移除電子和完全弛豫晶格來形成空穴極化子，體系的電中性通過補償背景電荷來保持。對于這樣的體系，必須應用“Initial Kick”來誘導極化子的形成，如果沒有“Initial Kick”，超胞會被弛豫到一個局部極小值，而空穴也會在整個晶體離域，不會形成極化子52。通過“Initial Kick”，無極化子的超胞會比有極化子的超胞能量更高，這充分說明了極化子研究中廣泛存在局域最小值問題，以及“Initial Kick”等初始擾動方法的重要性。

5.2 過渡金屬強關聯相互作用(Strong Correlation)和帶隙值修正問題

當研究體系含有過渡金屬時，會有所謂的“強關聯相互作用”，鋰離子電池正極材料中的過渡金屬與周圍氧原子間就被認為存在這樣的強關聯相互作用，而傳統DFT方法通常被認為不能準確描述這樣的強關聯相互作用，其泛函描述的電子過于離域，研究極化子可能會有嚴重誤差55,56。為修正該誤差，通常需要外加一個被稱為HubbardU的參數，通常稱這樣的方法為DFT+U方法。鋰離子電池正極材料所含過渡金屬元素的常用U值如表2所示57。

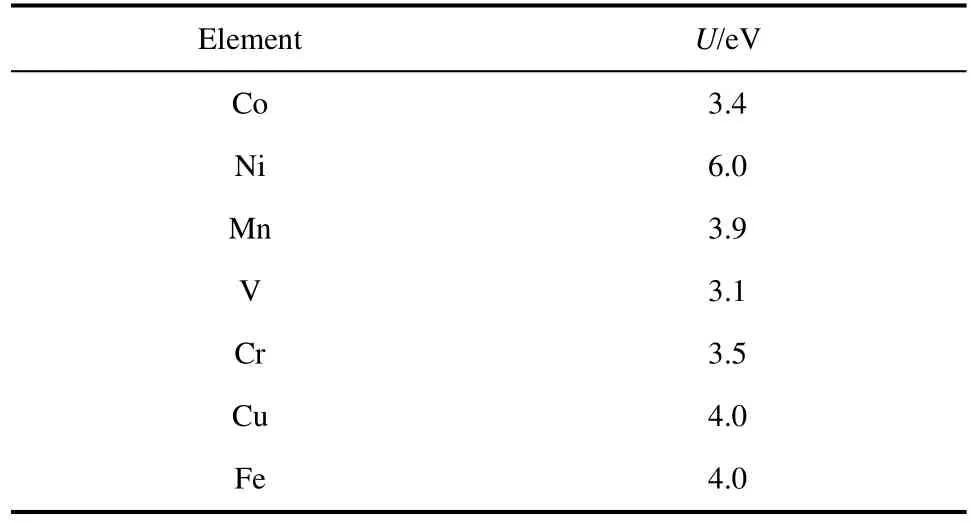
表2 鋰離子電池正極材料所含過渡金屬元素的常用U值57Table 2 Commonly used U values of transition metals in cathode materials of LIBs 57.

上文提到，根據固體能帶理論，我們可以通過一個體系帶隙值的大小將其分為絕緣體、半導體和導體，我們關心的極化子態也需要相對準確的帶隙值，因此，我們通過理論計算方法得到的帶隙值是否準確就顯得十分重要。遺憾的是，傳統DFT方法會嚴重低估帶隙值。當體系含有過渡金屬氧化物時，上文提到的DFT+U方法可以在一定程度上修正帶隙值，但修正后的結果通常仍會低于實驗值。因此，研究學者希望可以找到一些方法，來使得理論計算得到的帶隙值與實際實驗得到的帶隙值盡可能接近。通過研究發現，目前學界認為DFT計算會低估帶隙值的原因是由于傳統DFT方法選用的交換關聯泛函項會在一定程度上使得原本應該局域的電荷被計算得相對離域，從而無法準確刻畫電荷在空間的分布。由于DFT計算的電荷比真實情況更加離域，其波函數在空間內的重疊部分會增多，進而導致電荷之間的能量差變小，因此會在計算中得到比真實值更小的帶隙，這對于極化子的研究是不利的。與DFT恰好相反地是，傳統量子化學的從頭算Hatree-Fock方法通常會使得電荷的計算結果比實際更加局域，可以形象地用圖15表示。因此，加拿大蒙特利爾大學Matthias Ernzerhof教授課題組提出了一種將Hatree-Fock方法和DFT方法混合使用的雜化密度泛函方法(Hybrid Density Functional)，即在計算時，交換關聯泛函項混用25% (α= 0.25)的Hatree-Fock計算項和75% (1 –α= 0.75)的DFT計算項。這種泛函簡稱為HSE泛函，通過調整混合參數α，能很好地修正帶隙值58。HSE泛函通常被認為是當前第一性原理計算可行方案中精準度最高的泛函，但它對計算資源消耗很大，通常需要相對較多的計算時間，是一種比較昂貴的泛函。Johannes等55在研究LiMPO4(M = Fe, Mn, Co, Ni)時論述了HSE和DFT+U兩種計算方法的對比。他們指出，兩種方法都能對傳統DFT進行修正，但會對電子結構造成截然不同的影響。由于DFT+U僅修正了有“強關聯作用”相關的能帶(在他們的研究體系中，特指過渡金屬的d電子軌道)，而其他能帶不受影響，這就導致了被電子占據的d軌道會在能量上更加接近O的p軌道，這一能量差異的減小會進一步導致原本由過渡金屬原子d軌道主導的價帶頂行為受到O的p軌道雜化影響。如果隨著O的p軌道雜化量逐漸增大，可能會得出與實際物理過程不符的結論，而HSE的修正由于不僅僅針對“強關聯作用”相關的能帶，則不存在這一問題。他們選擇了結合能這一表征電子結構的關鍵參數作為驗證，將HSE和DFT+U關于結合能的計算數據與X射線光電子能譜(XPS)的實驗數據進行對比，發現HSE取得的結合能計算結果在峰型和峰位上與XPS實驗數據幾乎完美匹配，而DFT+U的結果則有著較大的差異，驗證了他們的理論解釋，如圖16所示。此外，不同體系的U值選擇有時候也會是一個麻煩的問題，無需根據不同體系選取不同U值也是HSE雜化泛函的優勢之一。因此，盡管在極化子的研究中有著大量DFT+U的計算工作，但由于極化子對電子結構的精度要求很高，為盡可能避免由于計算精度引起的錯誤結果，我們目前通常是推薦采用HSE雜化泛函來研究極化子。

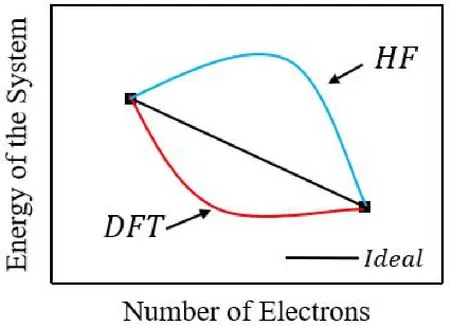
圖15 DFT計算方法與Hatree-Fock計算方法對于電荷計算差異示意圖Fig. 15 Schematic diagram of difference between DFT method and Hatree-Fock method for charge calculation.

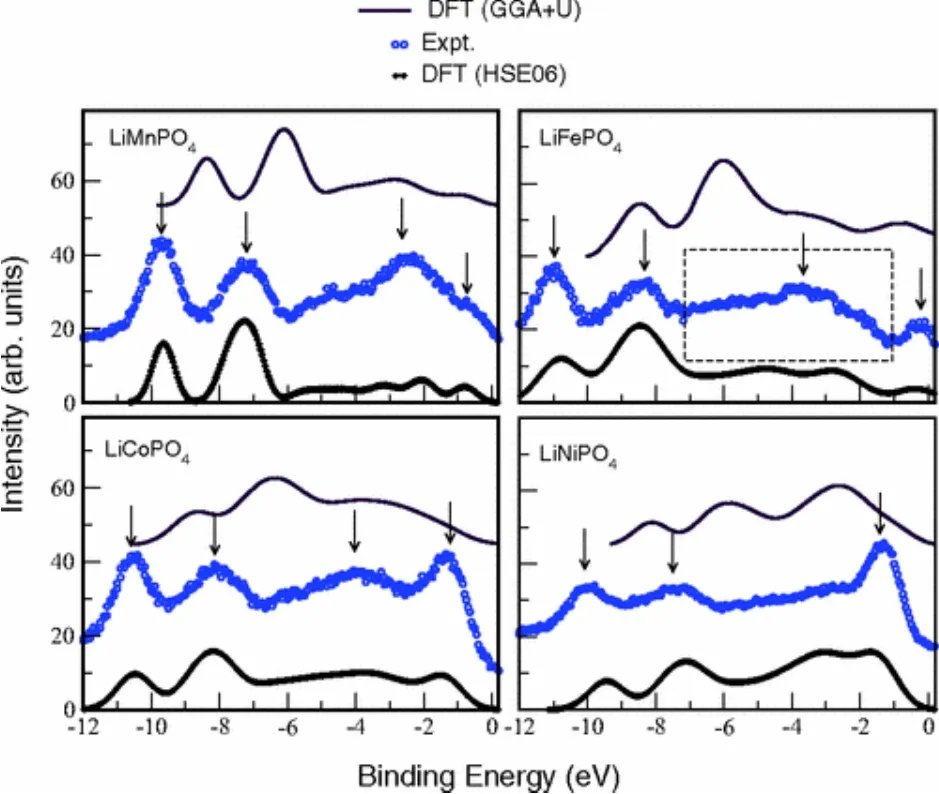
圖16 HSE和DFT+U兩種計算方法與XPS實驗數據關于結合能的對比55Fig. 16 The binding energy calculated by HSE and DFT+U compared with experimental XPS data 55.

此外，還有很多別的方法可以修正帶隙值，如Lany-Zunger方法(Lany-Zunger Approach)27、Wannier-Koopmans方 法 (Wannier-Koopmans Method)59、SCAN泛函等60，這些方法都能很好地修正帶隙值，從而為研究極化子提供更為精細的計算保障。

6 總結與展望

極化子現象目前在正極材料的研究中已引起廣泛關注，本文從極化子的理論計算判別方法、極化子對常見類型正極材料導電性能的影響、極化子調控策略和當前研究方法的一些理論難題對這一現象進行了綜述。總體而言，極化子會減弱體系的電子導電性，是磷酸鐵鋰等正極材料導電性能差的根本原因；但它又可能在一定程度上增強體系的結構穩定性，像一把“雙刃劍”。

提高正極材料的導電性能是鋰離子電池進一步發展的關鍵因素，為設計性能更加優越的正極材料，結合對極化子現象研究現狀的分析，在未來圍繞以下兩個方面展開系統性研究很有必要：首先，從基礎研究的角度看，目前人們對于極化子現象的形成機理仍未有清晰的認識。根據其“自陷作用”理論，很多材料都有運動電子和正負離子，但并不是所有材料都能形成極化子，其“自陷作用”的條件或程度的界定仍有待研究；搞清楚極化子的形成是否有可定量描述的物理化學規律、是否存在判斷極化子普適的充分必要條件，以及極化子與其它已知的物理化學現象(如Jahn-Teller畸變、Ni/Li反位、電聲耦合作用等)之間是否存在相互作用關系等問題，能幫助我們更加深刻地認識極化子，進而開拓基礎學科的認知邊界。其次，從應用角度看，正極材料哪些體系會出現/不出現極化子、為什么會出現/不出現極化子、極化子能否人為精細調控、如何在極化子對于材料導電性的降低和穩定性的提升之間實現平衡等問題，都是會對鋰離子電池正極材料的應用產生重要影響的關鍵性研究問題。