不同卸荷路徑下的頁巖蠕變特性試驗研究

王空前， 謝東武

(1.鄭州財經學院土木工程學院， 鄭州 450000； 2.同濟大學土木工程學院地下建筑與工程系， 上海 200092)

巖石流變力學與地下硐室設計、施工和運營安全緊密關聯，同時也是當下的研究熱點內容之一[1-2]。地下硐室圍巖在受擾動前處于三向應力狀態，工程實踐表明硐室開挖后巖體時效變形顯著，圍巖隨著時間發展，變形位移不斷累積，最終可能導致硐室坍塌，因此研究巖石三軸卸荷蠕變特性具有重要意義[3-4]。本研究背景為某深埋礦井巷道，巷道開挖后圍巖蠕變現象顯著，最終導致塌方，故而研究巖石的卸荷蠕變力學特性很有必要。

目前關于巖石卸荷蠕變特性的研究已取得一定成果：張龍云[5]以花崗巖為研究對象，開展三軸卸荷流變試驗，研究其卸荷流變變形、速率和強度等變化；石振明等[6]以綠片巖為試驗對象，設計恒定軸壓分級卸圍壓應力路徑下，開展蠕變試驗，分析軸向、側向蠕變規律；黃興等[7]開展砂質泥巖恒軸壓逐級卸圍壓蠕變試驗，研究卸荷流變中偏應力-應變關系及流變應變變化規律，分析砂質泥巖的擴容效應；楊超等[8]針對裂隙大理巖試樣，開展恒軸壓分級卸圍壓三軸卸荷蠕變試驗，研究試樣在不同裂隙傾角下的卸荷蠕變應變，探索完整巖石與裂隙巖體間卸荷蠕變的相關關系。目前卸荷應力路徑下的巖石蠕變特性研究相比常規加載應力路徑下較少，開展巖石卸荷蠕變試驗是系統性認識巖石流變特性的有效途徑之一。

由于目前的巖石卸荷流變試驗多為恒軸壓卸圍壓的應力路徑，與工程實踐中應力釋放方式存在一定偏差，故設計軸壓與圍壓等比卸荷的應力路徑，與傳統應力路徑進行對比試驗。其中，等比卸荷即徑向應力σ3與軸向應力σ1之比σ3/σ1為常數，該應力路徑多見于高邊坡、地下硐室，此類工程大部分區域內巖體開挖期間主應力比為常數[5]。現依托于某深埋礦井巷道工程實踐，以頂板頁巖為研究對象，開展不同卸荷路徑下的蠕變試驗，對比分析頁巖的軸向和側向應變特征、應變速率及長期強度，研究成果可為地下硐室長期穩定性研究提供一定參考。

1 頁巖卸荷蠕變試驗設計

1.1 試樣制備及基本力學參數

試樣取自某深埋礦井巷道頂板新鮮頁巖，巖層為志留系上統沙帽組，巖塊呈黑褐色層狀，巖樣基本物理力學參數如表1所示。

表1 巖樣基本物理力學參數

為了研究頁巖在三向應力強度特性，采用TLW-2000型巖石三軸流變試驗儀，將巖樣加工成φ50 mm×100 mm的圓柱樣(圖1)，開展三軸壓縮試驗，圍壓設置為20 MPa，軸向應力σ1與軸向應變ε1關系曲線如圖2所示。

圖1 巖石試樣照片

由圖2可看出，頁巖試樣A-1和A-2在圍壓20 MPa下的最大軸向應力分別為106.46 MPa和99.42 MPa，其平均值為102.94 MPa。

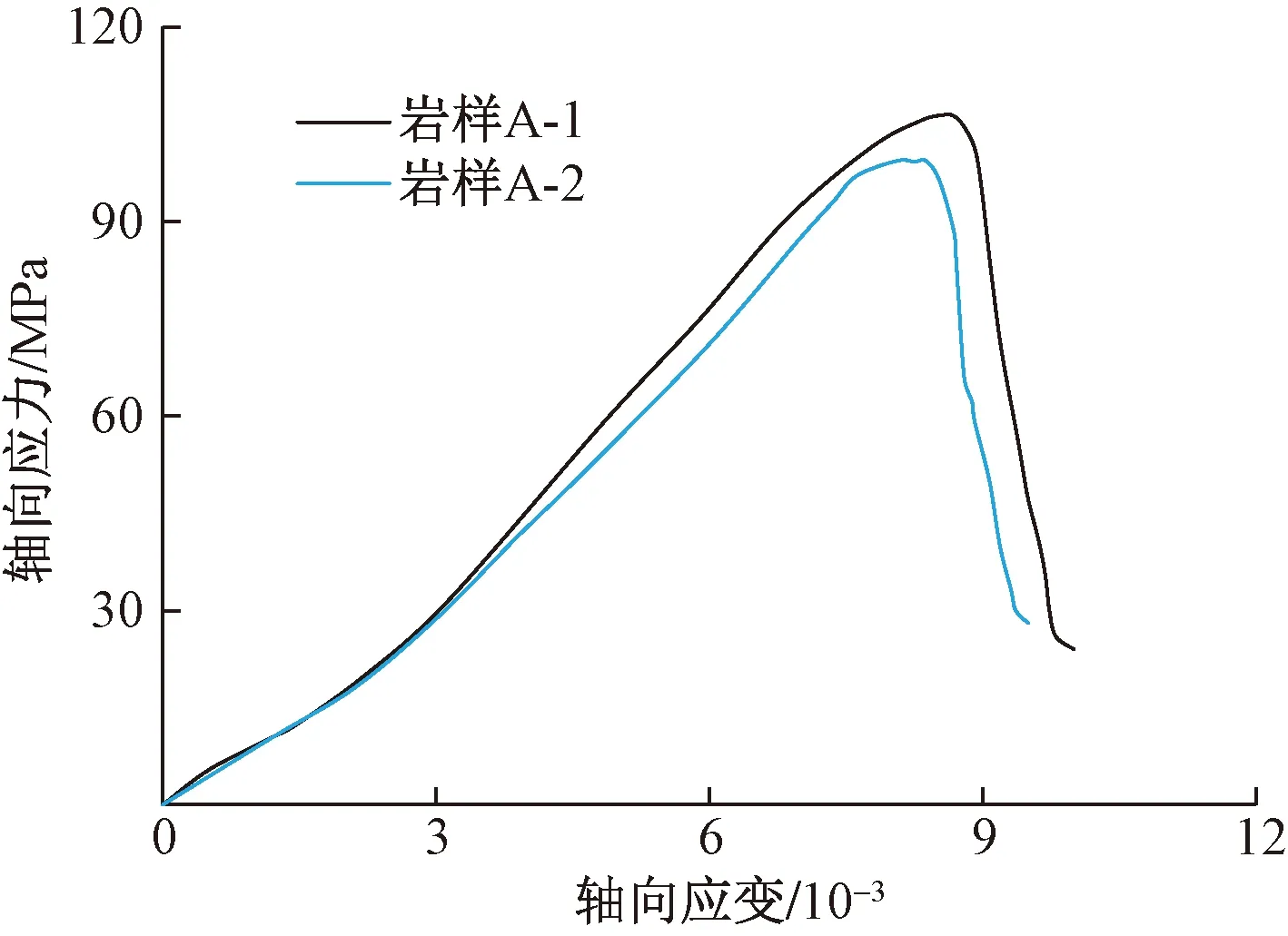
圖2 應力-應變曲線

1.2 卸荷蠕變試驗設計

卸荷蠕變試驗采用與三軸壓縮試驗相同的TLW-2000型巖石三軸流變試驗儀，設計兩種應力路徑：應力路徑Ⅰ為恒軸壓卸圍壓，應力路徑Ⅱ為軸壓和圍壓等比卸荷。應力路徑示意圖如圖3所示。

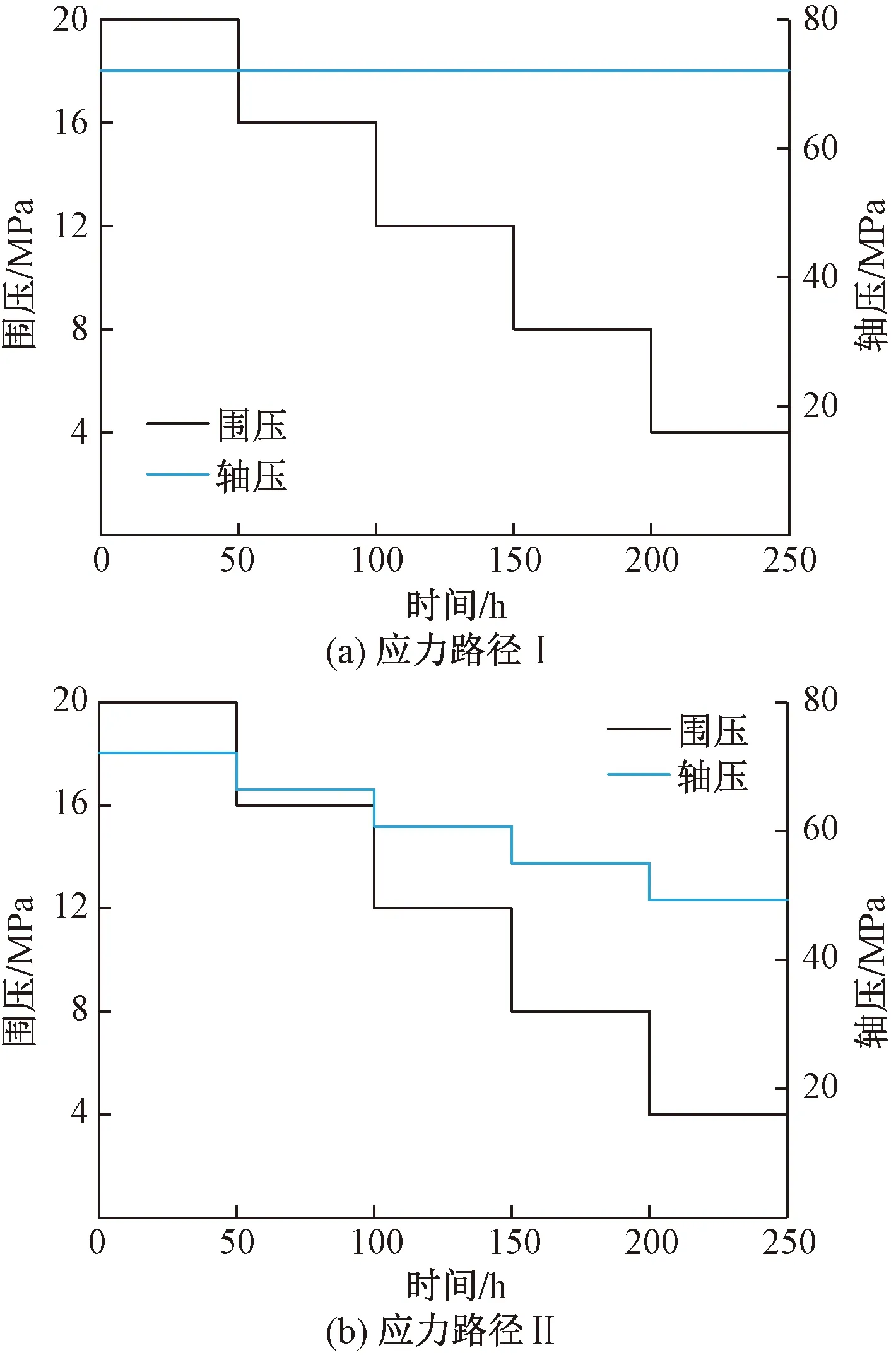
圖3 應力路徑圖

應力路徑Ⅰ：初始圍壓設置為20 MPa，初始軸壓取頁巖三軸試驗中最大軸向應力平均值的70%，即72.1 MPa。初始軸壓保持不變，圍壓以4 MPa為應力梯度進行卸載，直至試樣破壞。步驟為：首先以0.1 MPa/s的速率加載圍壓σ3到20 MPa，應力穩定后以0.1 MPa/s的速率加載軸壓σ1到72.1 MPa。軸壓σ1達到目標值后，觀察巖樣的軸向、側向位移，當其穩定后，保持軸壓恒定，以0.1 MPa/s的速率卸載圍壓，每4 MPa為一個應力梯度，每卸一級圍壓，至少保持50 h時間使蠕變變形充分發展，然后再繼續卸載，直至巖樣破壞。

應力路徑Ⅱ：初始圍壓設置為20 MPa，初始軸壓取頁巖三軸試驗中最大軸向應力平均值的70%，即72.1 MPa。圍壓以4 MPa為應力梯度進行卸載，軸壓以同樣比例(σ3/σ1=70%)進行卸載，即5.7 MPa，圍壓和軸壓等比卸荷，直至試樣破壞。步驟為：首先以0.1 MPa/s的速率加載圍壓σ3到20 MPa，應力穩定后以0.1 MPa/s的速率加載軸壓σ1到72.1 MPa。軸壓σ1達到目標值后，觀察巖樣的軸向、側向位移，當其穩定后，保持軸壓恒定，以0.1 MPa/s的速率同時卸載圍壓和軸壓，圍壓以4 MPa為應力梯度進行卸載，軸壓以5.7 MPa為應力梯度進行卸載，每一級卸載后至少保持50 h時間使蠕變變形充分發展，然后再繼續卸載，直至巖樣破壞。

1.3 卸荷蠕變試驗結果

兩種應力路徑下的頁巖卸荷蠕變試驗結果如圖4、圖5所示，其中圖4為頁巖在應力路徑Ⅰ下的(恒軸壓卸圍壓)軸向、側向應變隨時間累積曲線，圖5為頁巖在應力路徑Ⅱ下的(等比卸荷)軸向、側向應變隨時間累積曲線。

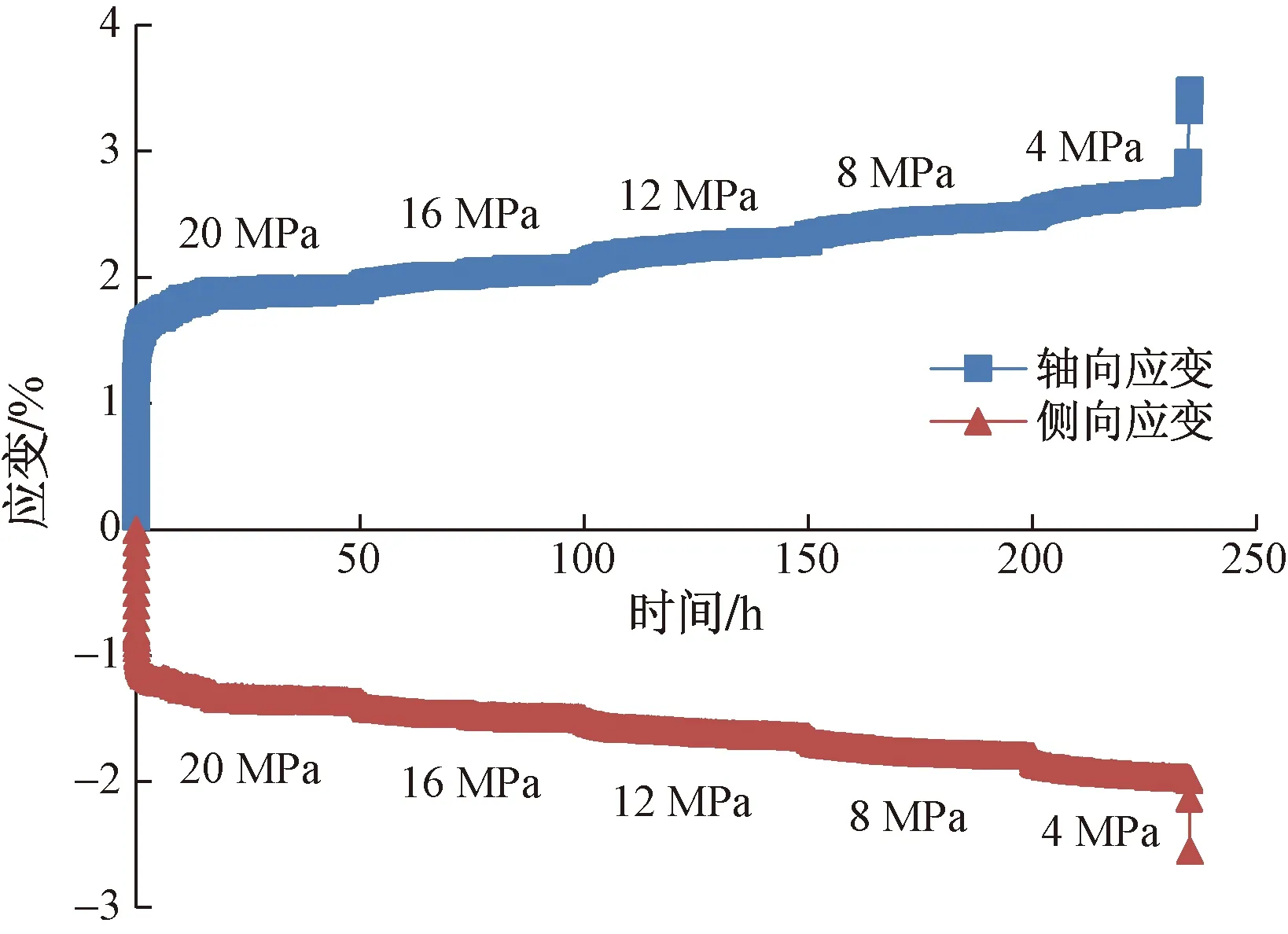
圖4 恒軸壓卸圍壓蠕變曲線

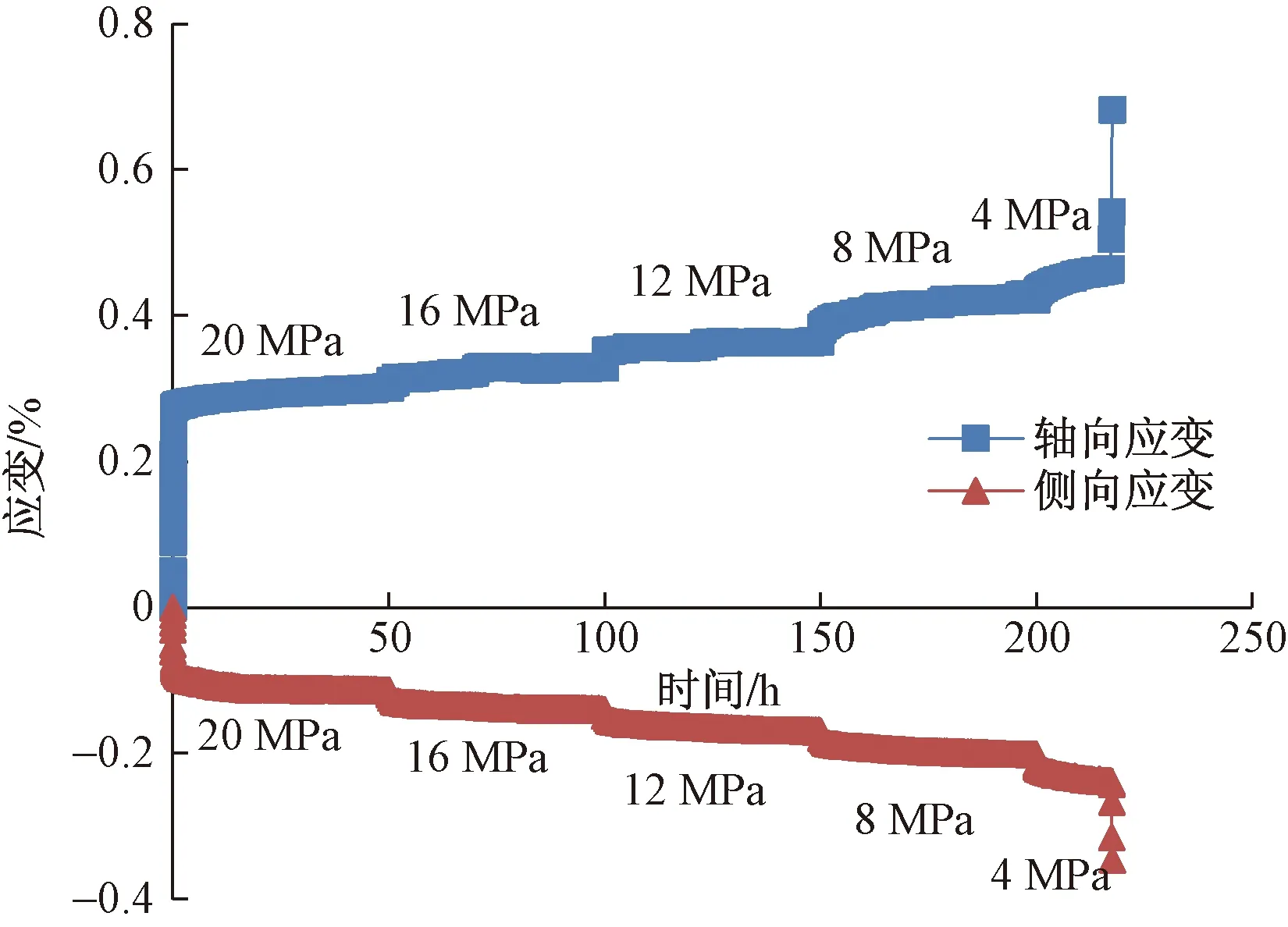
圖5 等比卸荷蠕變曲線

由圖4可看出，在軸壓恒定(72.1 MPa)的條件下，從20 MPa開始逐級卸載圍壓(4 MPa為應力梯度)，至第5級應力水平時巖石屈服破壞。此時，歷經234.52 h軸向應變達到最大值3.481×10-2，側向應變達到最大值-2.549×10-2。

由圖5可知，軸壓從72.1 MPa開始逐級卸載(應力梯度為5.7 MPa)，圍壓從20 MPa開始逐級卸載(4 MPa為應力梯度)，至第5級應力水平時巖石屈服破壞。此時，歷經217.55 h軸向應變達到最大值0.683×10-2，側向應變達到最大值-0.345×10-2。

綜合圖4、圖5可知，頁巖在應力卸荷條件下具有顯著的流變特性，在應力路徑Ⅰ、Ⅱ下的卸荷蠕變曲線形態基本一致。頁巖的軸向、側向應變均由瞬時應變和蠕變應變組成，在第1～4級加卸載等級下，頁巖蠕變出現衰減及穩定蠕變階段，直至最后一級應力，頁巖發生加速蠕變行為，巖石宏觀破壞。

2 試驗結果分析

2.1 卸荷蠕變曲線分析

通過Boltzmann線性疊加[9-10]處理圖4、圖5后得到分別卸載蠕變曲線，如圖6所示。

分析圖6(a)、圖6(b)，應力路徑Ⅰ下的軸向、側向應變差異在1.5倍以內，每一級軸向應變量值皆大于側向應變。在應力路徑Ⅰ條件下，巖石到達最后一級應力水平前，軸向應變為2.488×10-2，側向應變為-1.797×10-2，在破壞圍壓應力下分別增長為3.481×10-2和-2.549×10-2，增長部分分別占軸向和側向總應變的28.53%和29.50%。側向應變的變化程度大于軸向應變，體現出頁巖卸荷蠕變的擴容現象，側向擴容相較軸向擴容更為明顯。

再分析圖6(c)、圖6(d)，等比卸荷條件下的軸向和側向應變量值相差不大，差異在2倍以內，每一級軸向應變量值皆大于側向應變。在應力路徑Ⅱ條件下，巖石到達最后一級應力水平前，軸向應變為0.429×10-2，側向應變為-0.201×10-2。與應力路徑Ⅰ不同之處在于軸向應變發生瞬時卸荷回彈，軸向應變在第5級卸載瞬間從0.458×10-2變為0.445×10-2，隨即累積直至0.683×10-2，側向應變未見卸荷回彈現象，直接從-0.201×10-2變為-0.345×10-2。最后一級應力水平下，軸向、側向應變的增長分別占軸向、側向總應變的38.31%和41.74%，側向擴容相比軸向擴容更為顯著。

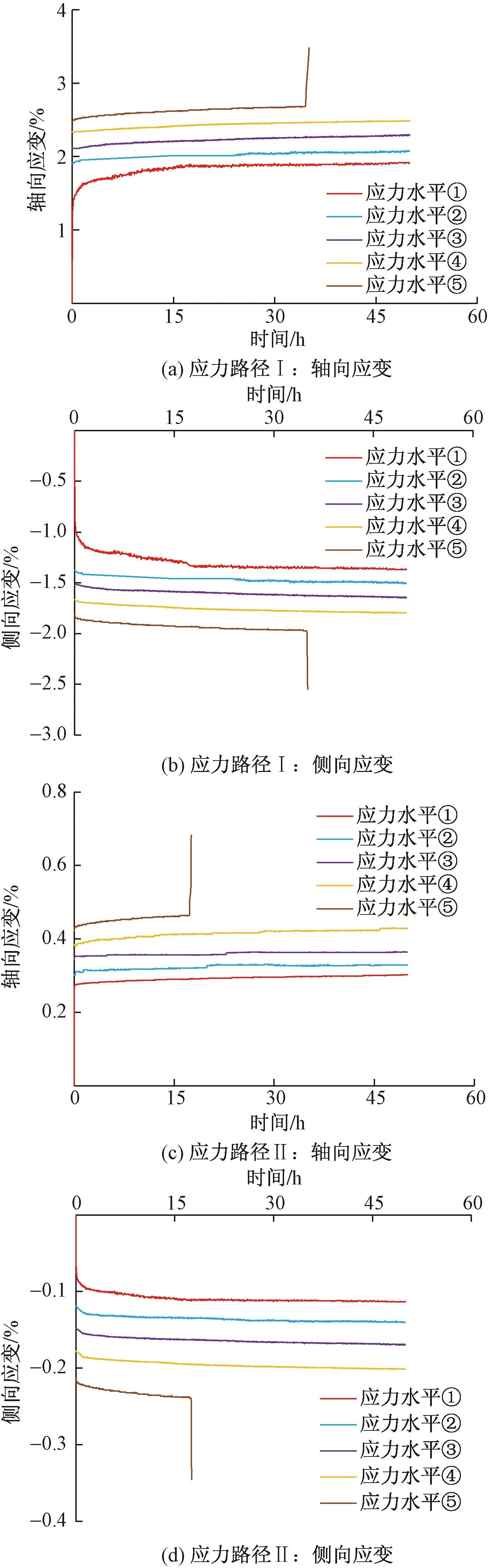
圖6 分別卸荷蠕變曲線

綜合圖6分析，兩種應力路徑下的分別卸載蠕變曲線特征大致相同，均在卸載瞬間產生瞬時軸向和側向應變，且第1級卸載產生的瞬時應變最大。分析兩種應力路徑下的第1級衰減蠕變階段，應力路徑Ⅰ下的衰減蠕變階段形態總體上相比應力路徑Ⅱ更為顯著，且歷時更長。在第1級卸載下，瞬時應變遠大于第2～5級，分析其原因可能為：頁巖自身發育一定微裂紋，微裂紋在應力場作用下處于較穩定的階段，當卸去部分荷載后，巖石彈性骨架的彈性變形性質得到發揮，微裂紋瞬間擴展，導致瞬時應變顯著增大。

2.2 瞬時、蠕變應變特征

將兩種應力路徑下的頁巖瞬時、蠕變應變進行統計，如表2所列。圖7、圖8分別為巖石瞬時應變和蠕變應變對比曲線，由圖6可知在兩種應力路徑下，第1級軸向、側向瞬時應變遠大于第2～5級，為了便于觀察第2～5級瞬時應變變化規律，圖7中省去第1級瞬時應變。

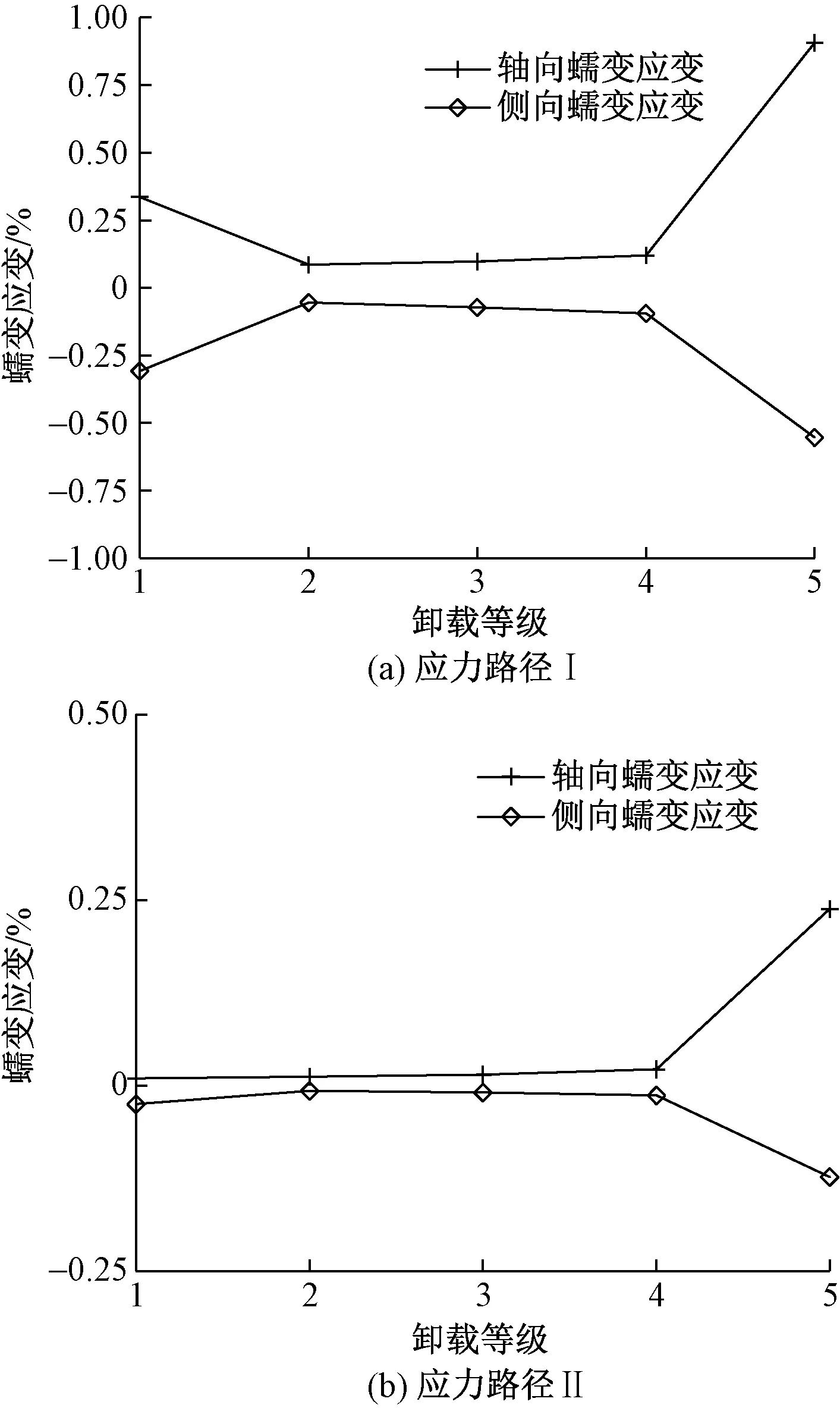
圖8 蠕變應變對比曲線

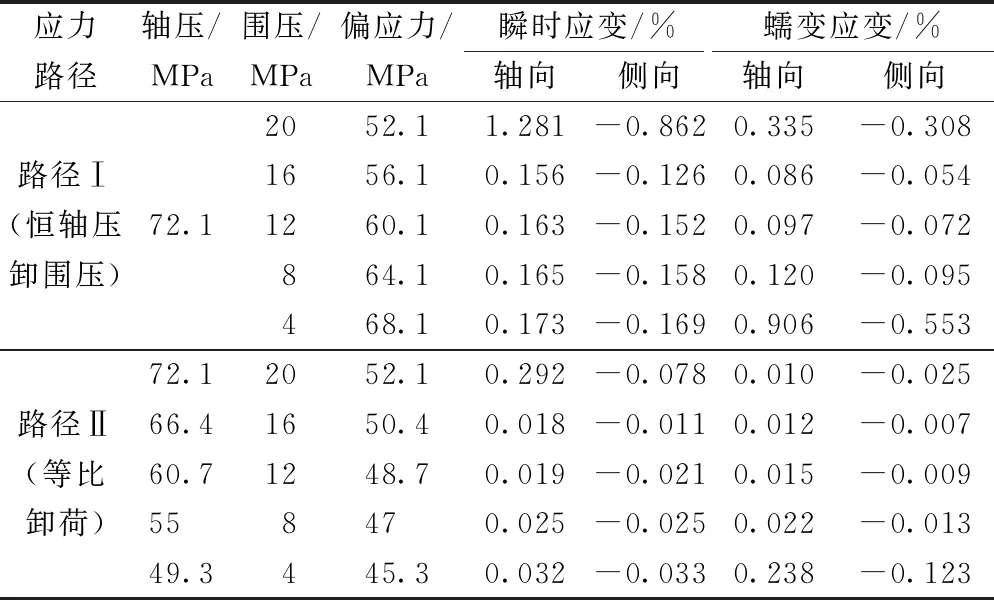
表2 兩種應力路徑下頁巖瞬時、蠕變應變

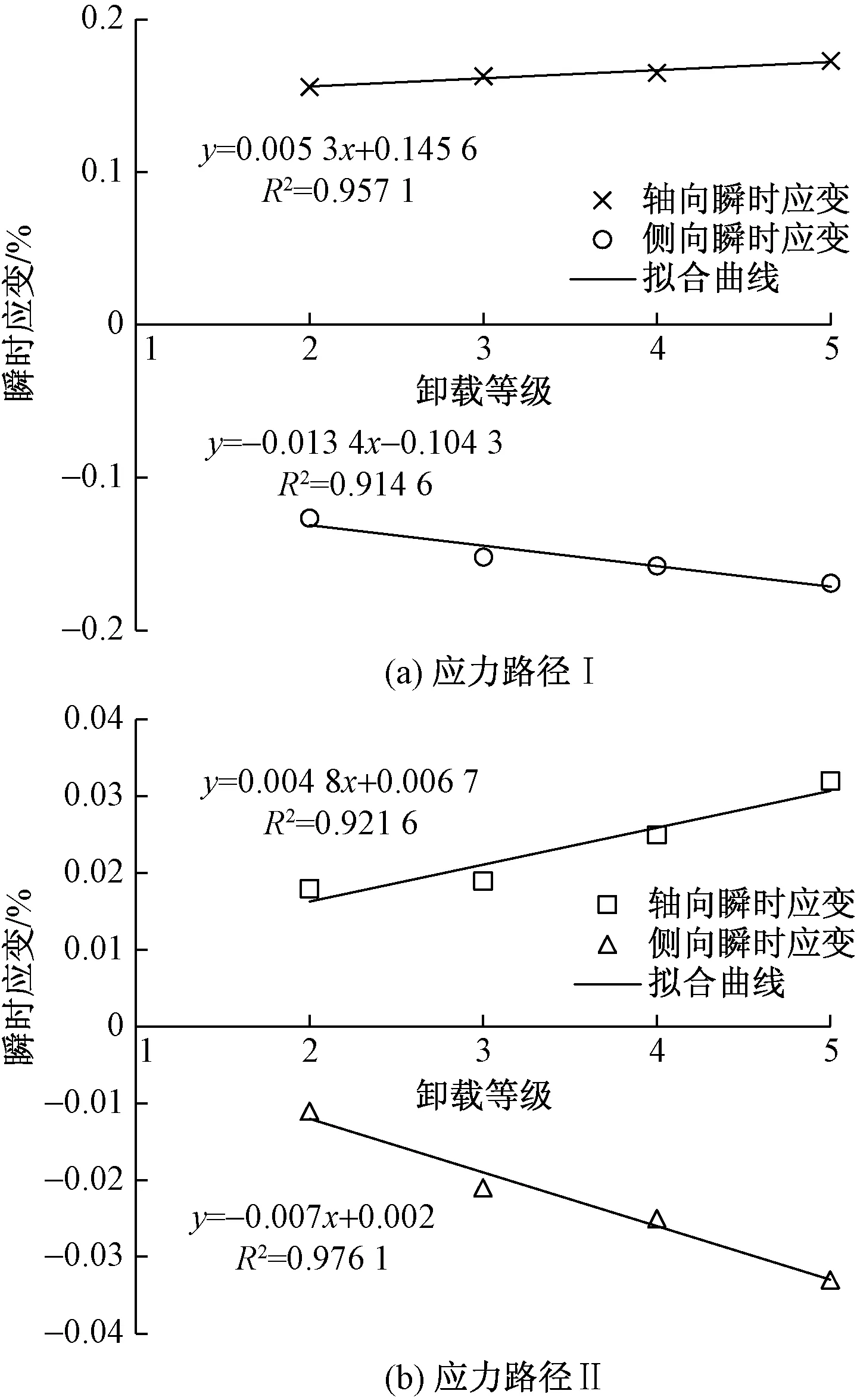
圖7 瞬時應變對比曲線

由表2可知，應力路徑Ⅰ第1級軸向、側向瞬時應變分別為1.281×10-2和-0.862×10-2，再結合圖7(a)中第2～5的應變節點可知，在同一卸載等級下，應力路徑Ⅰ下的頁巖的軸向瞬時應變量值均大于側向，軸向瞬時應變的線性增長趨勢略小于側向瞬時應變。應力路徑Ⅱ第1級軸向、側向瞬時應變分別為0.292×10-2和-0.078×10-2，圖7(b)中第2～5級側向瞬時應變量值均小于軸向，側向瞬時應變的線性增長趨勢大于軸向瞬時應變。綜合圖7可得，第2～5級軸向、側向瞬時應變均隨卸載等級的增加呈線性增大趨勢。

由圖8可看出，在恒軸壓卸圍壓條件下，軸向、側向蠕變應變從第1～2級先減小，第2～4級緩慢遞增，最后一級急劇增大。而在等比卸荷條件下，第1～4級軸向、側向蠕變應變緩慢遞增，最后一級顯著增大。再由圖2和表3可知，應力路徑Ⅰ的偏應力遞增，應力路徑Ⅱ的偏應力遞減，故而在兩種應力路徑下，巖石軸向、側向蠕變應變從第1～2級的變化規律差異顯著。

2.3 蠕變速率

張春陽等[11]針對逐級增量加載蠕變試驗提出蠕變速率求取方法，由于本文中卸荷蠕變試驗亦是逐級卸載，所以可參考張春陽等[11]提出的求取方法，即

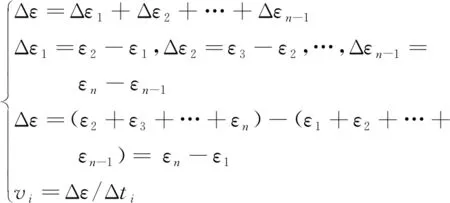
(1)

式(1)中：ε為蠕變應變；Δti為蠕變時間；n為蠕變試驗數據個數；vi為應變速率。

由于圖5、圖6中的蠕變曲線簇性態較為相似，第1～4級加卸載等級未發生加速蠕變，故以最后一級應力水平下的蠕變曲線為研究對象，通過式(1)的方法計算蠕變速率并繪制成圖，如圖9所示，限于篇幅，僅給出應力路徑Ⅰ下的第5級蠕變速率曲線。

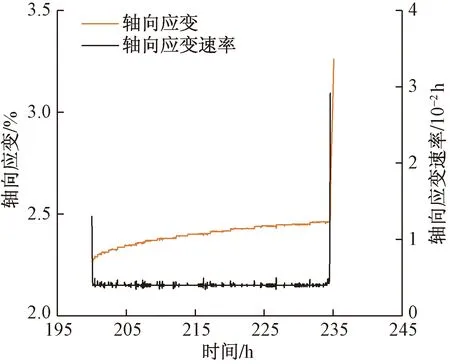
圖9 應力路徑Ⅰ：軸向蠕變速率曲線

由圖9可看出，應力路徑Ⅰ下的最后一級軸向蠕變速率先由某一數值(初始蠕變速率為1.302×10-2h)快速降低，接著在較長時間內保持恒定(穩態蠕變速率為0.409×10-2h)，最后急劇升高至一個最大值(極限加速蠕變速率為2.916×10-2h)，巖樣破裂。為了細致觀察頁巖加速蠕變階段及其與穩定蠕變階段的“過渡區間”[12]的蠕變速率變化規律，選取兩種應力路徑的軸向、側向蠕變速率局部節點繪制成圖，如圖10所示。

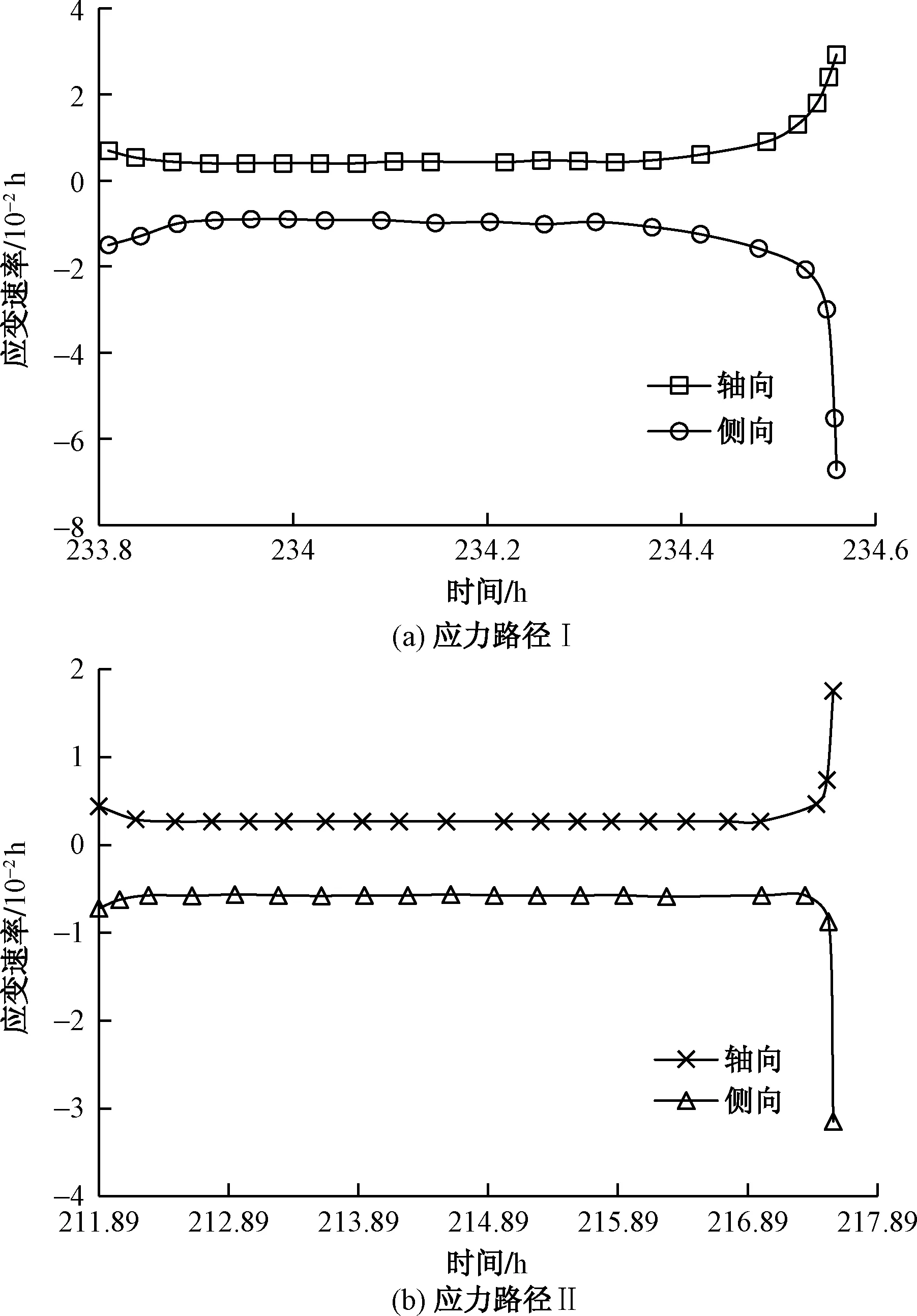
圖10 蠕變速率局部曲線

由圖10可看出，在巖石加速蠕變階段及其與穩定蠕變階段的“過渡區間”，蠕變速率先微降，再保持相對穩定，最后急劇增加。應力路徑Ⅰ中，這個過程僅持續0.71 h，軸向、側向應變分別達到0.778×10-2和0.575×10-2。而在應力路徑Ⅱ中，“過渡區間”和加速蠕變階段僅持續5.66 h，軸向、側向應變分別達到0.215×10-2和0.099×10-2。這說明巖體開挖卸荷后，當達到破壞應力水平后，圍巖可能發生大變形等不良現象，工程實踐中應做好監測工作。

兩種應力路徑中，側向蠕變速率都高于軸向，是軸向的2～2.5倍，巖石側向擴容不可忽視。等比卸荷的蠕變速率及蠕變變形皆不及恒軸壓卸圍壓，且等比卸荷的軸向應變在從第4～5級應力水平下發生回彈，這說明巖石在應力路徑Ⅱ(等比卸荷)中發生卸荷蠕變破壞的可預見性較小，圍巖監測時應引起重視。

2.4 長期強度

巖石逐級增量加載蠕變研究中，等時應力-應變曲線簇法是一種應用廣泛的長期強度求取方法[13-15]，由于本文中卸載蠕變試驗也是逐級進行應力卸載，且通過Boltzmann線性疊加原理進行數據處理，得到了分別卸載蠕變曲線(圖6)，所以亦可通過等時應力-應變曲線簇法基于圖6確定頁巖卸載蠕變的長期強度。選取0～50 h共6個時間節點，其中0 h為時間趨近于0的某一節點，以應力路徑Ⅰ為例，等時偏應力-應變曲線如圖11所示。

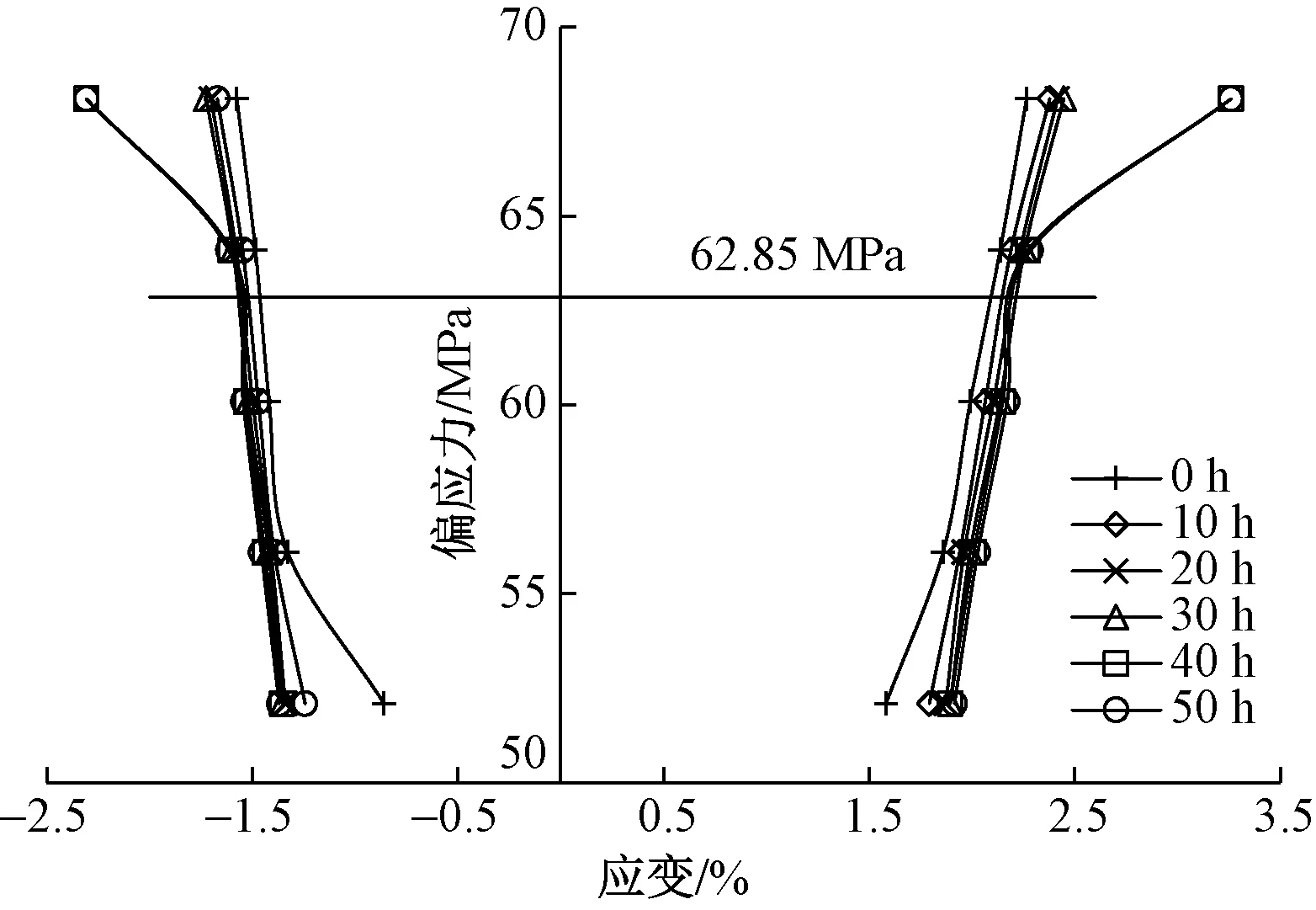
圖11 應力路徑Ⅰ：等時偏應力-應變曲線

在圖11蠕變曲線簇中取拐點，確定應力路徑Ⅰ條件下頁巖卸載蠕變長期強度為62.85 MPa。通過同樣的方法，確定應力路徑Ⅱ中長期強度為 47.69 MPa，相比應力路徑Ⅰ低15.16 MPa，頁巖三軸壓縮強度為102.94 MPa，長期強度在應力路徑Ⅰ和Ⅱ條件下分別折減了38.95%和53.67%，這說明巖石在等比卸荷應力條件下更易屈服破壞。

3 結論

(1)巖石在軸壓、圍壓等比例卸荷及恒軸壓卸圍壓應力條件下，巖石蠕變發展趨勢基本一致，巖石屈服破壞前均經歷衰減、穩定蠕變階段，當應力條件達到破壞應力水平時，巖石發生加速蠕變行為。

(2)在兩種應力路徑下，頁巖每一級應力水平的軸向應變量值皆大于側向應變。在達到最后一級應力水平前，側向應變的變化程度大于軸向應變，體現出頁巖卸荷蠕變的擴容現象，側向擴容相較軸向擴容更為明顯。

(3)兩種應力路徑中，側向蠕變速率都高于軸向，是軸向的2～2.5倍。等比卸荷的軸向、側向蠕變速率和變形量都不及恒軸壓卸圍壓，且等比卸荷的軸向應變在從第4～5級應力水平下發生回彈，這說明巖石在應力路徑Ⅱ(等比卸荷)中發生蠕變破壞的可預見性較小，圍巖監測時應引起重視。

(4)頁巖在恒軸壓卸圍壓和等比卸荷應力路徑中，長期強度分別為62.85 MPa和47.69 MPa，巖石在等比卸荷應力條件下更易屈服破壞，工程實踐中應考慮長期強度折減問題。

(5)本文研究背景為流變現象顯著的深埋礦井巷道圍巖，建議施工過程采取必要的支護及監測手段，削弱巖體卸荷引起的時效變形，以維持地下硐室的長期穩定性。