爬壁機器人底盤結構全向移動自主控制設計

郭家偉，談 波，陳 華，吳 昊

（1.馬鞍山學院大阪醫工學院，安徽 馬鞍山 243100；2沈陽建筑大學，遼寧 沈陽 110168）

1 引言

機器人作為電子與機械的結構化和智能化最好的體現，被廣泛地應用在生活和生產中[1]。在不同的領域中機器人可以代替或協助人工完成各種復雜的任務，尤其在垂直作業環境中，爬壁機器人有效降低作業風險、提高工作效率[2-4]。爬壁機器人通過不同的移動方式可以到不同的區域進行移動作業，因此研究機器人底盤結構全向移動控制意義重大。

目前研究通過底盤電機控制機器人全向移動的方法較多，文獻[5]利用旋轉電位器計算機器人底盤單元對應的偏轉角度，通過電機驅動器控制底盤運動，實現了全向移動機器人的控制。文獻[6]將可編程邏輯控制器作為機器底盤的控制器，以研究輪轂電動機和伺服電動機的運動控制為主，并對其進行運動學分析，根據分析結果同步控制8個電動機，實現移動機器人的移動控制。文獻[7]以機器人瞬時旋轉中心作為切入點進行研究。將底盤視為一個剛體，提出了一種估計關節空間內底盤瞬時旋轉中心的算法，精確計算底盤瞬時旋轉中心的位置估計值，從而實現底盤全向移動的控制。

在機器人運動學約束方面，文獻[8]提出一種爬壁機器人準全向控制方法，考慮粘附系統運動學約束，通過預定的模糊控制方法最大化機器人的可操作性，減少結構的動態干擾，做到機器人平穩導航；同時也有文獻[9]考慮工業檢測環境，以爬壁機器人無損檢測為前提，裝配便攜式傳感器以提高運動與黏著機制的適應性。以上研究成果在其設定的環境中取得了較好的機器人移動控制結果，總體來說，在爬壁機器人運動姿態的穩定控制與路徑控制精度方面可以進一步完善。

因此，研究了爬壁機器人底盤結構全向移動自主控制方法，利用卡爾曼濾波器預測、觀測、更新解算機器人姿態，以提高移動穩定性，在爬壁機器人運動學模型和動力學模型的基礎上，通過PID控制算法離散處理輸入誤差，實現爬壁機器人底盤結構全向移動的自主控制。

2 機器人運動學與動力學建模

2.1 坐標系變換

因爬壁機器人的移動方式是平行移動及旋轉移動，所以根據運動需求精準轉換坐標系。設R(θ)代表的是機器人體坐標系到場地坐標系之間存在的旋轉矩陣，其表達式為：

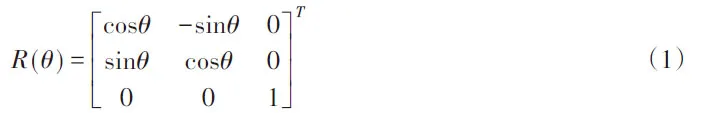
式中：θ—機器人兩個坐標x的姿態角。設R-1(θ)代表的是旋轉矩陣R(θ)對應的逆矩陣，實現逆向行駛，其表達式為：

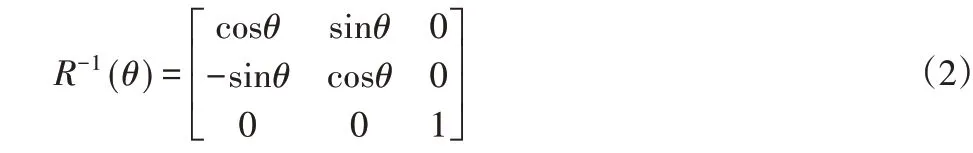
設Vx、Vy、W代表的是場地坐標系下存在的速度指令；vx、vy、w代表的是機器人體坐標系下存在的速度質量，兩者之間的轉換關系如下：

通過式（4）將機器人體坐標系中存在的速度指令vx、vy、w轉變到場地坐標系下存在的速度指令Vx、Vy、W：

至此，實現爬壁機器人體坐標系與場地坐標系的變換。

2.2 機器人動力學模型

機器人全向輪在無滑動條件下的速度分配受幾何分布的影響，在無滑動條件下機器人底盤四個輪子的速度分配方案是唯一的：

式中：Ri(i=1,2,3,4)—機器人中心與第i個全向輪質心之間存在的距離。在剛體轉動定律的基礎上獲得爬壁機器人底盤全向輪的轉動方程：

式中：Ti—驅動力矩；fi—摩擦力；j—全向輪轉動慣量；αi—全向輪對應的角加速度。

在全向輪坐標系下，機器人在運動過程中受到四個全向輪的牽引力，以及在機器人體坐標系下全向輪的轉動力矩和牽引力分量之間存在下述關系：

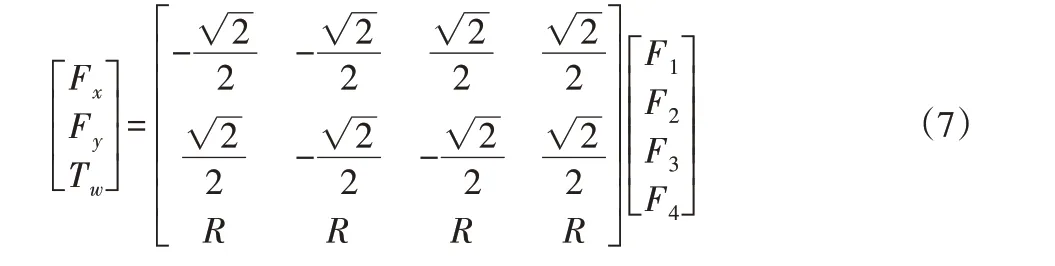
式中：Fx、Fy、Tw—機器人受到的牽引力或力矩。

聯立公式（7），獲得爬壁機器人的動力學模型：

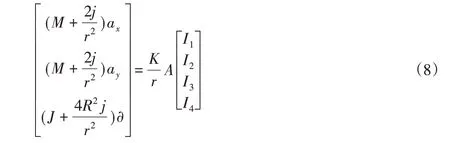
式中：M—車體質量；J—車體轉動慣量。

3 全向移動自主控制設計

3.1 姿態解算

爬壁機器人底盤結構全向移動自主控制設計方法利用卡爾曼濾波器對爬壁機器人的姿態進行解算。設z∈Rn代表的是離散時間狀態變量，通過卡爾曼濾波器對變量z進行估計[10]，通過下述公式描述變量z的離散隨機方差方程：

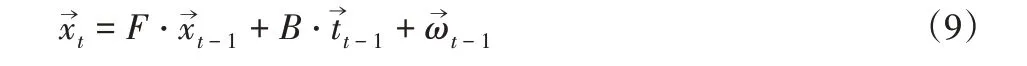
式中：—移動過程激勵噪聲。

爬壁機器人底盤結構全向移動自主控制設計方法為了方便計算通過四元數進行表示：

式中：q1—四元數的實部；q2、q3、q4—四元數的三維虛部。

在上述計算的基礎上，爬壁機器人底盤結構全向移動自主控制設計方法利用卡爾曼濾波器對爬壁機器人的姿態進行解算的過程如下：

（1）預測：用四元數代替角向量的過程如下：

對式（11）中存在的變量進行積分處理，對狀態值進行預測：

式中：δt—時間采樣周期；F—狀態變換矩陣。

為了模擬移動過程噪聲，需要對機器人陀螺儀各軸對應的方差進行估計，根據估計結果通過式（13）計算矩陣Q：

（2）觀測：機器人系統當前的狀態可以通過觀測值進行反映，通過測量磁力計信號和測量加速度計獲得機器人系統的觀測值。狀態空間可以通過矩陣Q映射到觀測空間中。

（3）更新：預測狀態可以通過加權求和進行更新：

式中：K—卡爾曼濾波器增益，其計算公式為：

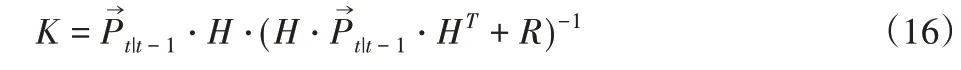
通過上述計算過程，可以實時預測、觀測并更新爬壁機器人的姿態，為移動自主控制提供基礎姿態數據。

3.2 移動自主控制

爬壁機器人底盤結構全向移動自主控制設計方法通過PID（Proportion Integration Differentiation）控制算法對爬壁機器人進行控制。PID控制器是通過線性組合微分環節、積分環節和比例環節構成的系統輸入控制量，通過控制量對爬壁機器人進行控制[11]。通過公式（26）描述PID控制器的控制規律：

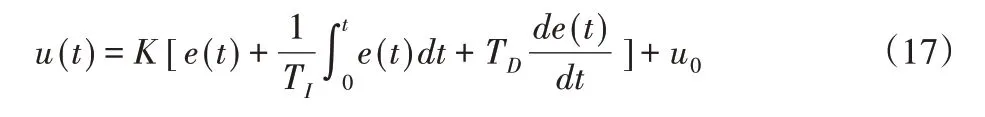
式中：u(t)—PID 控制器的輸出；u0—控制常量；TD—微分常數；TI—積分常數；e(t)—PID控制器的輸入，可通過輸出值y(t)與r(t)計算得到。

爬壁機器人底盤結構全向移動自主控制設計方法利用增量的形式代替微分，用累加的方式代替積分，在PID連續公式中引入離散處理的形式為：

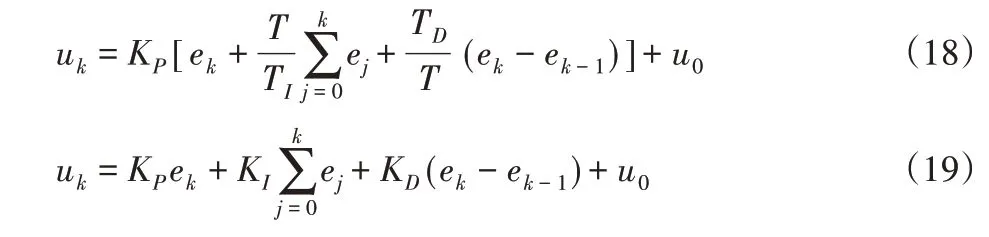
式中：ek—在第k次采樣中系統對應的輸入誤差；ek-1—在第k-1次采樣中系統對應的輸入誤差；T—采樣周期；TI—離散采樣時間；uk—在第k次采樣中系統對應的輸出值；u0—系統初始的控制值；KD、KI—微分環節系數、積分環節系數。

通過上述公式，獲得第k-1個采樣時刻控制器對應的輸出值：

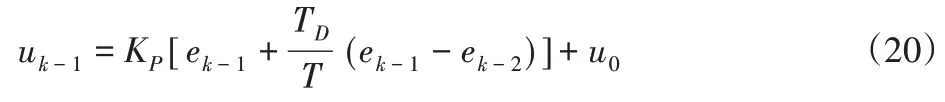
整理上述公式，獲得增量式PID控制算法公式，實現爬壁機器人底盤結構全向移動的自主控制：

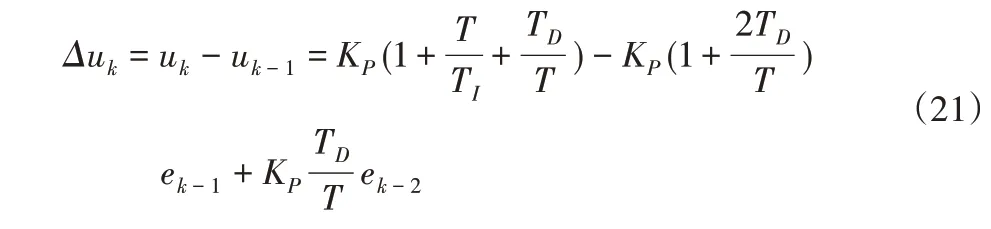
4 實驗結果與分析

4.1 實驗環境

為了驗證爬壁機器人底盤結構全向移動自主控制設計方法的整體有效性，需要對爬壁機器人底盤結構全向移動自主控制設計方法進行測試，本次測試在MATLAB 7.0平臺中完成。設計的機器人，所有四個車輪都通過軸承機構被動旋轉，而電機則放在前面，以實現各個車輪的轉向。用于連接的碳纖維管直徑為10mm，在傾斜伺服電機中內置過載傳感器，該模型的角分辨率為0.323°，0.166s/60°的速度以及12 kg f.cm的失速扭矩，工作角度為320°并支持連續旋轉。并集成了用于角運動和轉矩控制的PID控制器，能夠定義其速度、最小/最大操作角度以及影響其通信協議的其他參數。

4.2 實驗與分析

分別采用爬壁機器人底盤結構全向移動自主控制設計方法（方法1）、基于ST Nucleo-F446RE 的全向移動機器人控制方法（方法2）和基于運動學分析的全向移動機器人控制方法（方法3）進行測試。設置平穩性因子，在區間[1，10]內取值，平穩性因子越高表明控制方法的平穩性越好。平穩因子計算公式為：

式中：Ru—機器人重心到旋轉軸的距離；θ—Ru與垂直平面的夾角；φ—水平面旋轉傾斜角。

平穩不同方法的測試結果，如圖1所示。

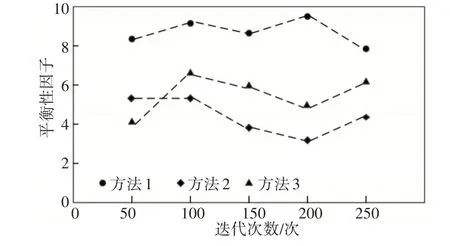
圖1 不同方法的平穩性因子Fig.1 Stationarity Factors of Different Methods

分析圖1可知，方法1在多次迭代中獲得的平穩性因子平均在7以上，遠遠高于方法2和方法3在多次迭代中獲得的平穩性因子。平穩性因子越高，表明方法控制的爬壁機器人平穩性越好。因為方法1利用卡爾曼濾波器對爬壁機器人的姿態進行解算，解算過程通過預測、觀測及更新等步驟及時調整校正機器人姿態，在爬壁機器人姿態信息的基礎上控制爬壁機器人的移動，得到了機器人平穩行進的控制效果。

將控制精準度作為指標，將實驗平面傾斜角度12°的平面進行精度控制實驗，進一步對方法1、方法2和方法3的整體有效性進行測試，與規劃好的路徑對比，偏差越小精準度越高。控制路徑曲線實驗環境，如圖2所示。

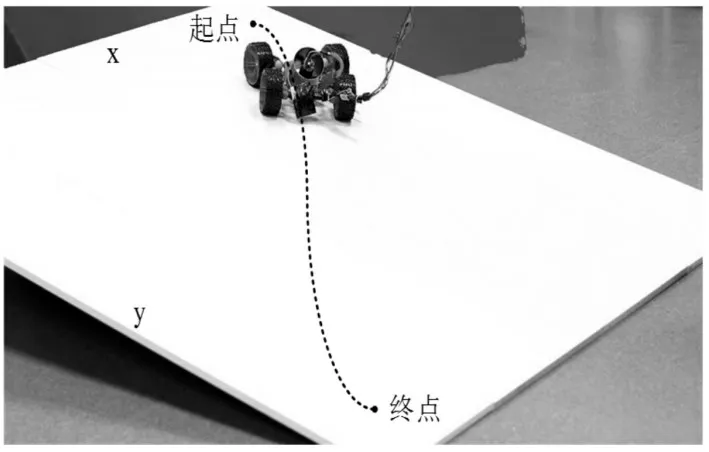
圖2 控制路徑曲線實驗環境Fig.2 Experimental Environment of Control Path Curve

不同方法的控制路徑實驗結果，如圖3所示。由圖3中的數據可知，采用方法1、方法2進行測試時，與規劃路徑的偏差較大。而方法1控制的路徑與規劃路徑幾乎相同。因為此次設計的方法在姿態更新解算的基礎上，利用增量的形式代替微分，能及時減少路徑輸入誤差，將PID控制算法進行離散處理，獲得增量化的控制算法，提高了機器人移動路徑的控制精度。

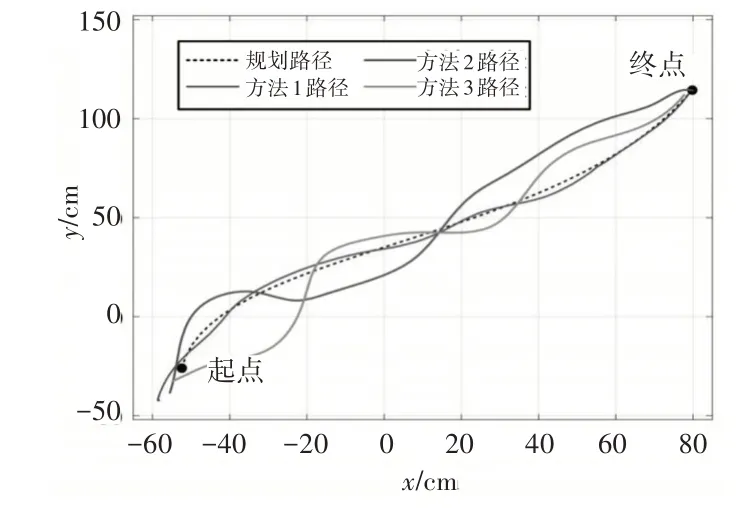
圖3 不同方法的控制路徑曲線Fig.3 Control Path Curves of Different Methods

5 結束語

研究了爬壁機器人移動控制的問題，利用卡爾曼濾波器預測更新機器人姿態，引入PID 控制算法離散化處理移動輸入誤差。經實驗驗證可以得出以下結論：（1）在迭代250次的平穩性實驗中，方法通過卡爾曼濾波器解算姿態下獲得了較高的平穩性因子，使得機器人的全向移動穩定性優于對比方法；（2）在傾斜角度12°的平面沿既定路徑行進時，通過PID控制提高了移動路徑控制的精準度，使得機器人行進路徑更貼合實際規劃路徑，減少了路徑誤差，使路徑移動控制性能優于對比的兩種方法。（3）爬壁機器人在移動過程中只通過底盤結構的控制難以消除移動平面不平造成的摩擦力負載環境的變化，因此需要在以后的工作和研究中考慮爬壁機器人位姿閉環控制器的設計。