SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS
ZHANG Ji-wei,ZHAO Cheng-chao
(1.School of Mathematics and Statistics,and Hubei Key Laboratory of Computational Science,Wuhan University,Wuhan 430072,China)
(2.Beijing Computational Science Research Center,Beijing 100193,China)
Abstract:While the variable time-steps two-step backward differentiation formula(BDF2)is valuable and widely used to capture the multi-scale dynamics of model solutions,the stability and convergence of BDF2 with variable time steps still remain incomplete.In this work,we revisit BDF2 scheme for linear diffusion-reaction problem.By using the technique of the discrete orthogonal convolution(DOC)kernels developed in[11],and introducing the concept of the discrete complementary convolution(DCC)kernels,we present that BDF2 scheme is unconditionally stable under a adjacent time-step ratio condition:0 Keywords:BDF2;DOC;DCC;variable time steps;sharp error estimate In this paper,we revisit two-step backward differentiation formula(BDF2)with variable time steps for solving the linear reaction-diffusion equation: where the reaction coefficient κ ∈ R,and Ω is a bounded domain. Set the generally nonuniform time levels 0=t0 Here rmaxis the positive real solution of x3=(2x+1)2,see the details in Lemma 2.1. For the sharp and robust convergence,we further express the local truncated error by an error convolution structure(ECS)with the BDF2 kernel,see more details in Lemma 3.9.Using the definition of DOC kernels,the ECS can significantly circumvent the complex calculation of BDF2 and DOC kernels.Thus,we have the sharp and robust second-order convergence under the ratio condition A1(i.e.0 The organization of the paper is given as follows.In Section 2,we present the semipositive definition of BDF2 kernels under condition A1,and the properties of DOC and DCC kernels.The stability analysis and second-order convergence of the BDF2 scheme(1.3)are given in Section 3.Numerical examples are provided to demonstrate our theoretical analysis. In this section,we first consider the positive semi-definiteness of BDF2 convolution kernels and the properties of DOC and DCC kernels,which are useful for the analysis of stability and convergence of BDF2 scheme in section 3. It is known that problem(1.1)with κ≤0 has the property of energy dissipation.We now present the corresponding energy stability for BDF2 scheme(1.4).To the end,we define a(modified)discrete energy Ekby The proof is complete. Table 1 Numerical accuracy on random time mesh for κ=0 Table 2 Numerical accuracy on random time mesh for κ=4 From the current data and more tests not listed here,we see that the BDF2 scheme is robustly stable and convergent in the second order,which is consistent with our theoretical analysis.Due to the time step is randomly chosen without any constrain condition,one can see the first-step BDF1 does not bring the loss of accuracy,which again implies the effectiveness of our analysis. With the applications of DCC and DOC kernels,we present the stability and convergence analysis of BDF2 scheme with variable time-steps under condition A1.We extend the adjacent time step to a new ratio rk:= τk/τk?1≤ rmax=4.8645,and obtain the robust and sharp second-order convergence without the extra constrained condition on ratios in[11].Our convergence results shows that the BDF1 scheme for first step is enough to have the globally optimal second-order convergence.This conclusion removes the doubt of the choice of the first level solution with first-order accuracy.Numerical results are provided to demonstrate the theoretical analysis. The technique developed in this work can be extended to a family of multi-step schemes with variable time-steps for the stability and convergence analysis.The main challenge is how to explore the useful properties of DOC and DCC kernels,and multi-step schemes’s kernels. Acknowledgements The authors would like to thank professor Tao Tang,professor Zhimin Zhang and Dr.Honglin Liao for their valuable discussions on this topic.1 Introduction
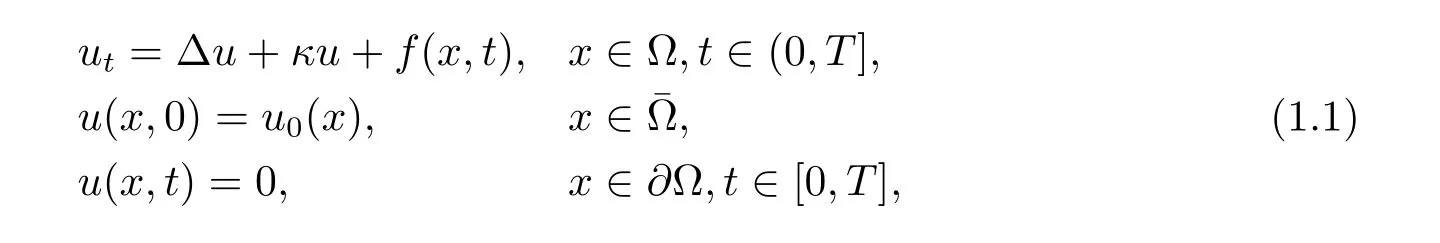


2 The Properties of BDF2,DOC and DCC Kernels
2.1 Positive Semi-Definiteness of BDF2 Convolution Kernels




2.2 The Relationship Between DOC and DCC Kernels


2.3 Properties of DOC and DCC Kernels


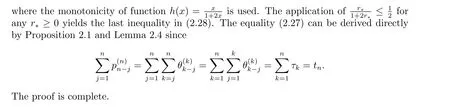
3 Stability and Convergence Analysis for BDF2 Scheme
3.1 Energy Stability


3.2 Stability Analysis of the Discrete Scheme



3.3 Convergence Analysis of the Discrete Scheme



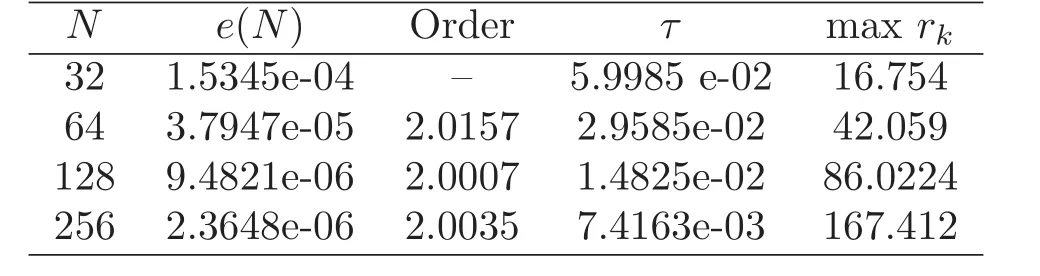
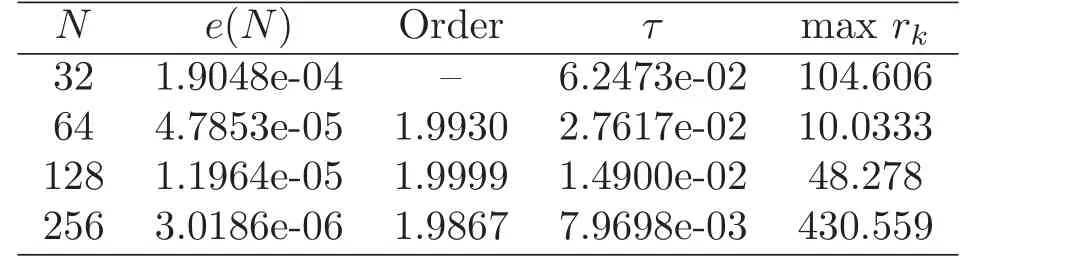
4 Numerical Experiment

5 Conclusion

