阿貝爾方程的兩個周期解的存在性
倪 華,胡瀟逸,姚怡萍,朱潔怡
(江蘇大學數學科學學院,江蘇 鎮江 212013)
1 引言
非線性阿貝爾方程
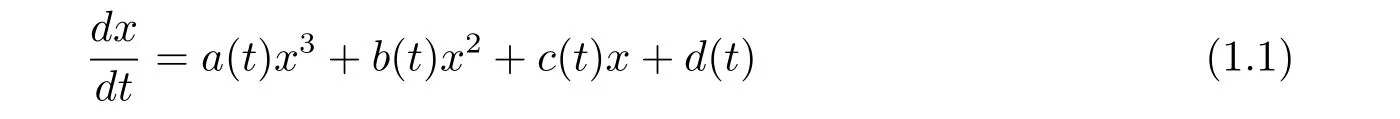
在物理和工程技術等許多領域有著重要應用[1?2],方程(1.1)的數學性質已被數學和物理學者[3?15]進行了深入研究.文獻[14,15]提出了得到阿貝爾方程的通解的一種方法,他們都假定y=y1(t)是方程(1.1)的一個特解,然后通過變量代換方法,給出了阿貝爾方程的通解;文獻[16]假設γ=γ(t)是阿貝爾方程的一個周期特解,然后,利用變量代換法和不動點定理,得到阿貝爾方程的其他周期解的存在性.
本文首先考慮下列阿貝爾型方程:

文獻[15]給出了方程(1.2)可積的充分必要條件,如下:
命題1.1[15]阿貝爾型方程(1.2)可積的充分必要條件是a(t),b(t)滿足下列條件:

其中k是常數.
在條件(1.3)成立時,b(t)/=0,(1.3)兩邊從t0到t(t>t0)積分,可得:


此時,a(t),b(t)不可能都是周期函數.因此,當a(t)和b(t)都是周期函數并且線性無關時,方程(1.2)是不可積的.
本文首先考慮a(t)和b(t)是周期函數時的微分方程(1.2),此時除了a(t)和b(t)線性相關外,(1.2)是不可積的.本文研究在不求出(1.2)的解的情況下,(1.2)的周期解的存在性.文獻[16]利用不動點定理,得到(1.2)的唯一非零周期解的存在性;本文受文獻[16]的啟發,利用不同于文獻[16]的方法,得到方程(1.2)的唯一非零周期解的存在性;然后,討論了方程(1.1),在一定條件下,利用變量代換法,將方程(1.1)轉化為方程(1.2),從而得到阿貝爾方程(1.1)的兩個周期解的存在性.
本文余下部分安排如下:第二節,我們給出四個引理以方便以后使用;第三節,利用不動點定理得到阿貝爾型方程存在唯一非零周期解的四個定理;第四節,當方程的系數函數滿足一定條件時,我們得到了阿貝爾方程的兩個周期解的存在性.
2 一些定義、引理和縮寫


3 阿貝爾型方程的唯一非零周期解的存在性









4 阿貝爾方程的兩個周期解的存在性


- 數學雜志的其它文章
- 分數階拉普拉斯方程的一種新型有限差分方法
- 一類非線性隨機微分方程的統計性質
- AN OPTIMAL DIVIDEND STRATEGY IN THE DISCRETE MODEL WHEN PAYMENTS ARE SUBJECT TO BOTH TRANSACTION COSTS AND TAXES
- DIFFERENTIAL MIXED EQUILIBRIUM PROBLEMS IN BANACH SPACE
- THE REPRESENTATION CATEGORIES OF DIAGONAL CROSSED PRODUCTS OF INFINITE-DIMENSIONAL COFROBENIUS HOPF ALGEBRAS
- APPROXIMATIONS OF THE IDENTITY ADAPTED TO CONTINUOUS ELLIPSOID COVER

