THE REPRESENTATION CATEGORIES OF DIAGONAL CROSSED PRODUCTS OF INFINITE-DIMENSIONAL COFROBENIUS HOPF ALGEBRAS
YANG Tao,LIU Hui-li
(College of Science,Nanjing Agricultural University,Nanjing 210095,China)
Abstract:The categorical interpretations on representations of diagonal crossed products of infinite-dimensional coFrobenius Hopf algebras are studied in this paper.By the tools of multiplier Hopf algebra and homological algebra theories,we get that the unital representation category of a diagonal crossed product of an infinite-dimensional coFrobenius Hopf algebra is isomorphic to its generalized Yetter-Drinfeld category,which generalizes the results of Panaite et al.in finitedimensional case.
Keywords:coFrobenius Hopf algebra;diagonal crossed product;Yetter-Drinfel’d module
1 Introduction
A Yetter-Drinfel’d module over a Hopf algebra,firstly introduced by Yetter(crossed bimodule in[1]),is a module and a comodule satisfying a certain compatibility condition.The main feature is that Yetter-Drinfel’d modules form a pre-braided monoidal category.Under favourable conditions(e.g.if the antipode of the Hopf algebra is bijective),the category is even braided(or quasisymmetric).Via a(pre-)braiding structure,the notion of Yetter-Drinfel’d module plays a part in the relations between quantum groups and knot theory.
When a Hopf algebra is finite-dimensional,the generalized(anti)Yetter-Drinfel’d module category was studied in[2].The authors showed thatHYDH(α,β) ~=H???H(α,β)M,where H??? H(α,β)is the diagonal crossed product algebra.Then one main question naturally arises:Does this isomorphism still hold for some infinite-dimensional Hopf algebra?
For this question,we first recall from our paper[3]the diagonal crossed product of an infinite-dimensional coFrobenius Hopf algebra,then we consider the representation category of the diagonal crossed product,and show that for a coFrobenius Hopf algebra H with its dual multiplier Hopf algebra^H,the unital^H ?? H(α,β)-module category is isomorphic to(α,β)-Yetter-Drinfeld module category introduced in[2,4],i.e.,HYDH(α,β) ~=^H??H(α,β)M.Moreover,as braided T-categories the representation category Rep(⊕(α,β)∈G^H ?? H(α,β))is isomorphic to YD(H)introduced in[2].
The paper is organized in the following way.In section 2,we recall some notions which will be used in the following,such as multiplier Hopf algebras and(α,β)-quantum double of an infinite dimensional coFrobenius Hopf algebra.
In section 3,we show that for a coFrobenius Hopf algebra H,the unital^H ?? H(α,β)-module category^H??H(α,β)M is isomorphic toHYDH(α,β).And as braided T-categories the representation theory Rep(A)is isomorphic to YD(H)introduced in[2],generalizing the classical result in[2,5].
2 Preliminaries
We begin this section with a short introduction to multiplier Hopf algebras.
Throughout this paper,all spaces we considered are over a fixed field K(such as thefield C of complex numbers).Algebras may or may not have units,but always should be non-degenerate,i.e.,the multiplication maps(viewed as bilinear forms)are non-degenerate.Recalling from the appendix in[6],the multiplier algebra M(A)of an algebra A is defined as the largest algebra with unit in which A is a dense ideal.
2.1 Multiplier Hopf Algebras
Now,we recall the definition of a multiplier Hopf algebra(see[6]for details).A comultiplication on an algebra A is a homomorphism Δ :A ?→ M(A?A)such that Δ(a)(1?b)and(a? 1)Δ(b)belong to A? A for all a,b ∈ A.We require Δ to be coassociative in the sense that
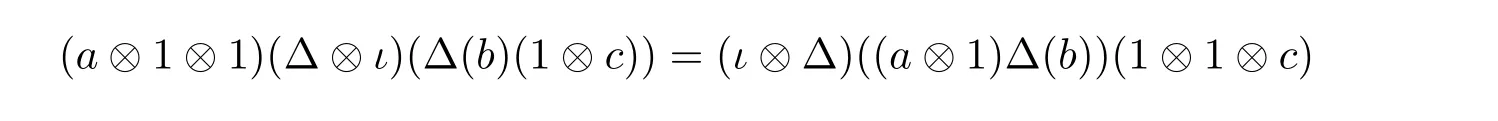
for all a,b,c ∈ A(where ι denotes the identity map).
A pair(A,Δ)of an algebra A with non-degenerate product and a comultiplication Δ on A is called a multiplier Hopf algebra,if the maps T1,T2:A?A?→M(A?A)defined by
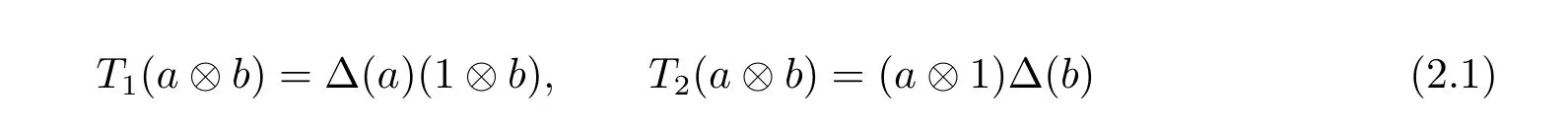
have range in A?A and are bijective.
A multiplier Hopf algebra(A,Δ)is called regular if(A,Δcop)is also a multiplier Hopf algebra,where Δcopdenotes the co-opposite comultiplication defined as Δcop= τ?Δ with τ the usual flip map from A?A to itself(and extended to M(A?A)).In this case,Δ(a)(b?1)and(1?a)Δ(b)∈A?A for all a,b∈A.
Multiplier Hopf algebra(A,Δ)is regular if and only if the antipode S is bijective from A to A(see[7],Proposition 2.9).In this situation,the comultiplication is also determined by the bijective maps T3,T4:A?A?→A?A defined as follows

2.2 Diagonal Crossed Product of an Infinite Dimensional coFrobenius Hopf Algebra


3 Representation Category of the Diagonal Crossed Product





