智慧公路設備橫梁風振特性研究

成 晟

(泰州市公路事業發展中心，泰州 225300)

隨著智慧公路發展，道路上的電子設備日益增多，設備橫梁多為定型鋼管，采用門架式或懸臂式，安裝在路側或道路上方。設備自重較輕，橫梁承載能力一般都滿足要求。但運營過程中發現，部分道路上空的設備橫梁會發生上下振動的現象，影響設備使用，還可能帶來安全隱患。

目前對振動問題的分析多采用有限元法，有限元法方便建模，隨著計算機算力提高，近些年得到了廣泛應用[1-2]，但有限元計算只能得到數值解，不能得到解析解，不便對結果進行數學解釋和原因分析。

本文基于等截面直梁的橫向振動模型，對門架式設備橫梁和懸臂式設備橫梁的振動進行了分析，得到的振動影響因子可以為結構設計提供參考。

1 振動特性分析

發生振動的門架式橫梁為等截面八角鋼管，跨徑22.5 m，跨中處采用法蘭對接，門架橫梁結構如圖1所示。安裝設備后，測得振動周期大約為0.55 s，對應的角頻率為11.42 rad/s。

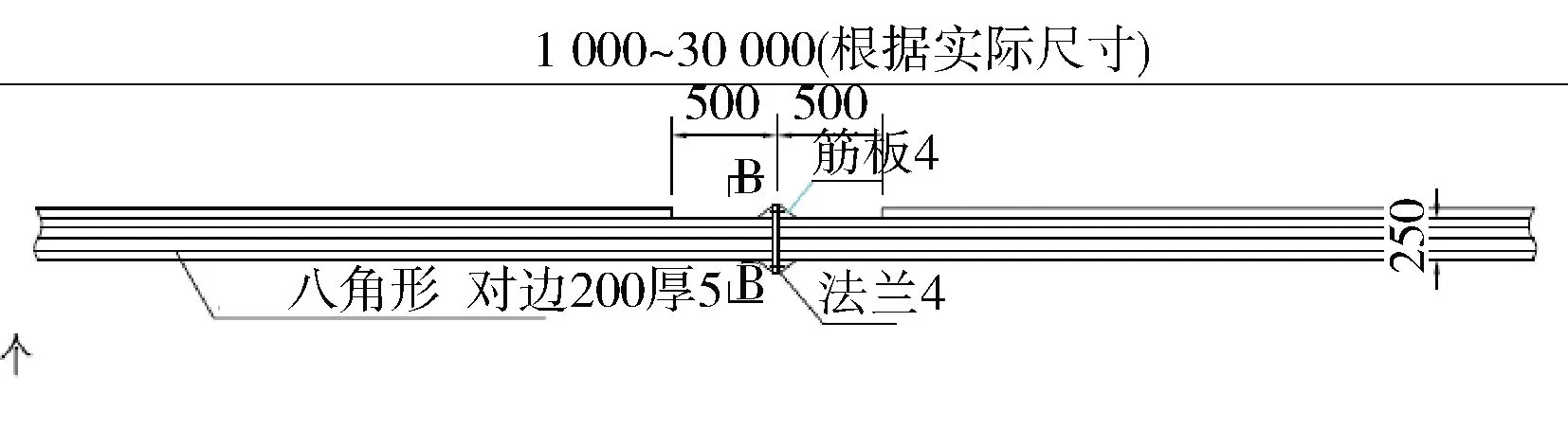
(a)立面結構(mm)

懸臂橫梁結構實景如圖2所示。懸臂式橫梁為跨徑7.25 m的圓管，外徑15.9 cm，壁厚6 mm，尚未安裝設備，測得振動周期大約為0.32 s，對應的角頻率為19.63 rad/s。

圖2 懸臂橫梁結構實景

觀測發現，橫梁振動有如下特征：

(1)振動時風速不大。

(2)不同時段的振幅不同，但頻率基本相同。

(3)橫梁上各點雖振幅不同，但相位始終相同，沿縱向不發生能量傳播，具備典型的駐波特征。

2 兩端固結等截面直梁的橫向振動

2.1 無阻尼自由振動

直梁橫向自由振動作為振動力學的經典問題，已有較多研究成果[3]。假設橫梁為歐拉-伯努利梁，不考慮截面的剪切變形和截面繞中心軸轉動的慣性效應。微元體受力如圖3所示。

圖3 微元體受力

彎矩和剪力的計算公式分別見式(1)和式(2)。

(1)

(2)

式中，M為彎矩，N·m；Q為剪力，N；w為橫向位移，m；E為楊氏模量，N/m2；I為截面慣性矩，m4；x為縱向距離，m。根據式(1)和式(2)可推導出等截面直梁的橫向自由振動方程，見式(3)。

(3)

式中，ρ為材料密度，kg/m3；S為截面積，m2；t為時間，s。

采用分離變量法，令橫向位移為

w(x,t)=φ(x)q(t)

(4)

代入式(3)，得到

等式兩邊同時除以ρSφ(x)q(t)，并令

得到

(5)

EIφ(4)(x)-ρSω2φ(x)=0

(6)

式中，wi為固有頻率，rad/s。

式(5)為單自由度線性振動方程，其通解為

q(t)=αsin(ωt+θ)

(7)

φ(4)(x)-β4φ(x)=0

(8)

利用指數形式特解φ(x)=eλx，代入式(8)可導出特征方程λ4-β4=0，繼而求得式(8)的通解為

φ(x)=C1cosβx+C2sinβx+C3chβx+C4shβx

(9)

式(7)和式(9)中的C和ω由梁的邊界條件確定，理論上存在無窮多個固有頻率ωi和對應的振型函數φi(x)。

一維簡諧波的駐波方程為

y=2Acoskxcosωt

(10)

式(10)中時間變量和位置變量相互獨立，表明各點的振動狀態不發生縱向傳播。對照式(4)和式(10)可知，分離變量解和駐波方程在形式上基本相同，因此振動橫梁上的駐波可看作式(3)的一個特解或幾個特解的疊加。當外部激勵力頻率ω0和系統的第k階固有頻率ωk接近時，第k階主坐標振動幅度急劇增大，產生第k階頻率的共振，并可近似忽略其他非共振的主坐標[3]。

邊界條件：固定端的位移和轉角都為0，即

φ(x)|x=0=0，φ(x)|x=L=0

φ′(x)|x=0=0

φ′(x)|x=L=0

(11)

式中，L為桿長，m。

代入式(9)，得到兩端固結等截面直梁橫向振動的控制方程為

cosβLcoshβL-1=0

(12)

將橫梁參數代入控制方程，通過數值求解，得到i為1、2、3時的角頻率ω分別為16.05 rad/s、44.25 rad/s、86.75 rad/s，以縱向位置x為橫坐標、相對振幅為縱坐標，可求得對應的振型，橫梁振型如圖4所示。實際橫梁的固有頻率受材料、結構、設備質量和施工誤差影響，和理論值存在偏差。

(a)i=1

因實際振動的橫梁上各點相位始終相同，故橫梁駐波主要對應于i=1時第一振型的共振。

2.2 阻尼自由振動

無阻尼自由振動是一種理想情況，實際系統不可避免存在阻尼因素。等截面直梁的橫向阻尼振動方程為

(13)

式中，c為黏性阻尼系數，N·s/m。

采用分離變量法，將式(4)代入式(13)，得到

(14)

等式兩邊同時除以ρSφ(x)q(t)，并令

得到

(15)

(16)

將特解q(t)=eλt代入式(16)，求得當ζ<1，系統處于欠阻尼狀態時的通解

q(t)=Ae-ζωtsin(ωdt+θ)

(17)

式中，A為初始幅值，m；θ為初相角，rad；ωd為阻尼自由振動的固有角頻率，rad/s。

(1)阻尼自由振動的振型函數φi(x)與無阻尼自由振動相同。

(2)因ωd<ω，故阻尼自由振動頻率小于無阻尼自由振動頻率。

(3)振幅與-ζωt呈指數關系，阻尼和固有頻率增大，都將導致阻尼自由振動的振幅迅速衰減。

2.3 受迫振動

實際橫梁振動是在外部荷載的持續激勵下產生的，因此需要對橫梁的受迫振動進行計算。因系統固有振型與阻尼、外部激勵無關，故可假設外荷載的空間分布與振型函數相同，以方便計算。

令外部激勵力為

F(t)=F0φ(x)eiω0t

(18)

F和F0單位為N，則受迫振動方程為

=F0φ(x)eiω0t

(19)

采用分離變量法，將式(4)代入式(18)，得到

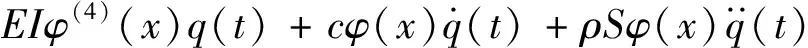
=F0φ(x)eiω0t

(20)

(21)

根據常微分方程理論，非齊次線性常微分方程式(21)的全解由齊次線性方程(15)的通解和非齊次線性方程(21)的特解兩部分組成。通解為阻尼自由振動，由于自由振動只在擾動初期短暫存在，隨即趨于衰減，故只需討論非齊次線性方程(21)的特解。簡諧激勵引起的穩態響應也是簡諧運動，故可令解的形式為q(t)=Qeiω0t，代入式(21)求得特解為

(22)

式中，f=ω0/ω為激勵頻率與固有頻率之比(無量綱)。

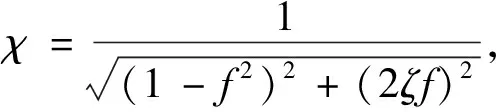
(a)ζ=0.1

由式(22)可知：

(1)受迫振動頻率和外部激勵頻率相同。

(2)受迫振動振幅受固有頻率、激勵頻率和阻尼影響，與固有頻率平方呈反比關系。當激勵頻率與固有頻率比值接近1時，振幅急劇增大；阻尼增大時，振幅放大因子減小。

2.4 計算分析

懸臂梁的邊界條件為：固定端的位移和轉角為0，自由端的彎矩和剪力為0。除邊界條件外，懸臂梁的振動方程和解析步驟與兩端固結等截面橫梁完全相同，故不再贅述。

代入橫梁實際尺寸，可求得自由振動情況下，門架式橫梁的固有振動周期為0.39 s，懸臂式橫梁的固有振動周期為0.34 s。

懸臂式橫梁的計算周期與實測周期接近，而門架式橫梁的計算周期與實測周期偏差較大，分析可能是因為懸臂式橫梁尚未安裝設備，而門架式橫梁上已安裝設備，設備會影響橫梁的固有振動頻率。

3 風荷載分析

在一定條件下的定常來流繞過鈍體時，物體兩側會周期性地交替脫落旋轉方向相反、排列規則的雙列線渦，稱為卡門渦街。由于旋渦交替脫落，產生的脈動荷載會使結構發生受迫振動[2, 4]。

空氣的雷諾數Re(無量綱)[5]計算公式為

Re=69 000vd

(23)

式中，v為計算流速，m/s；d為截面直徑，m。若圓柱體直徑取0.2 m，當風速為0.02～21.7 m/s時，代入式(23)可求得對應的雷諾數為300～300 000。

圓柱體的旋渦脫落頻率[6-7]為

(24)

式中，T為脫落周期，s；D為圓柱外徑，m；St為斯特勞哈爾數(無量綱)，主要與流體的雷諾數有關，當雷諾數為300～300 000時，St近似于常數值0.2[4]。

將外徑0.2 m、脫落周期0.55 s代入式(24)，不考慮橫梁上設備影響，求得門架式橫梁振動時對應的風速為1.82 m/s。將外徑0.159 m、脫落周期0.32 s代入式(24)，求得懸臂式橫梁振動對應的風速為2.48 m/s。江蘇泰州地區重現期10年的風速為24.5 m/s[5]。因此，設備橫梁會在風速較小時振動，與實際觀測一致。

4 固有頻率影響因子分析

4.1 尺寸影響分析

因八角鋼管與圓管外形相似，故本節用圓管代替八角鋼管進行模擬計算，取不同外徑、壁厚和跨徑組合，分別計算門架式橫梁無阻尼自由振動的固有頻率。固有頻率ω與外徑D呈正比關系，與跨徑L的平方呈反比關系，與壁厚無關，門架式橫梁固有角頻率影響因子如圖6所示。

圖6 門架式橫梁固有角頻率影響因子

固有頻率ω與外徑D和跨徑L的關系為

(25)

式中，ω為固有頻率，rad/s；D為外徑，m；L為跨徑，m。

同樣可求得懸臂式橫梁固有頻率與外徑、跨徑的關系。懸臂式橫梁固有角頻率影響因子如圖7所示，計算公式見式(26)。

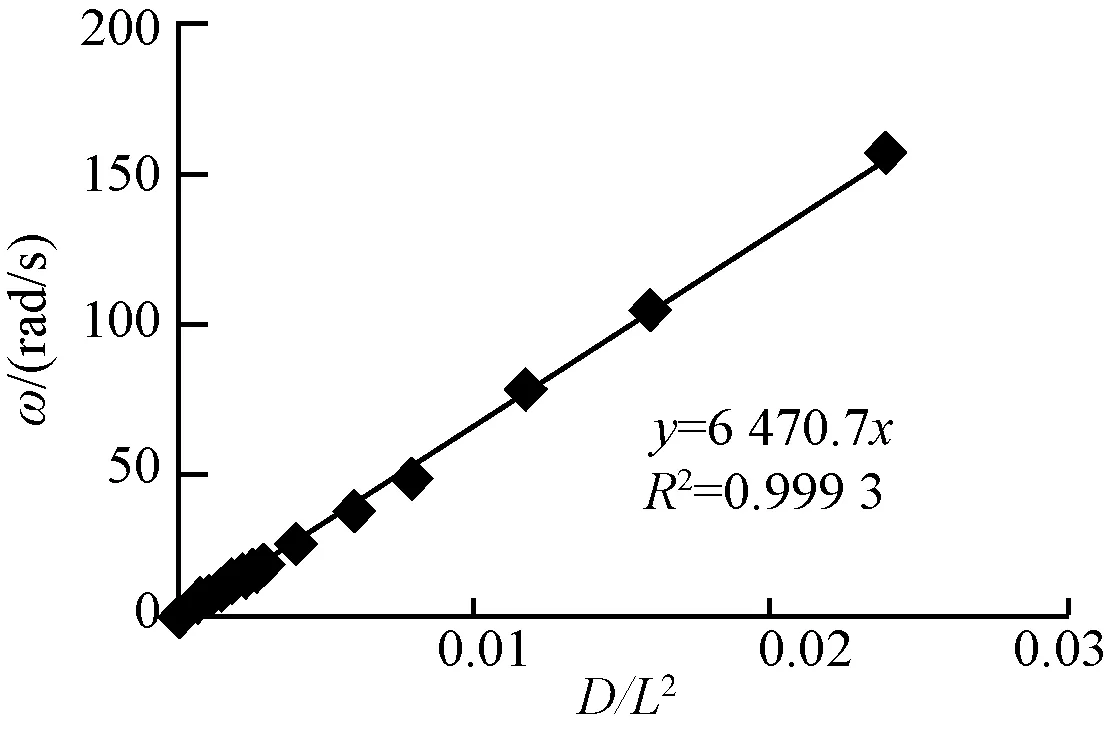
圖7 懸臂式橫梁固有角頻率影響因子

(26)

由式(25)和式(26)可知，加粗鋼管或減小跨徑都能提高固有頻率。

風速增大時，旋渦脫落頻率隨之增大，并接近部分小跨徑橫梁的固有頻率，但實際并未發現這類橫梁有明顯振動，這是因為式(22)中振幅與ω2呈反比關系，跨徑減小后固有頻率增大，抑制了受迫振動的振幅。

4.2 質量影響分析

為模擬設備質量對橫梁振動的影響，保持橫梁尺寸不變，改變橫梁密度，考察自由振動的固有頻率變化，質量對門架式橫梁固有角頻率的影響如圖8 所示。

圖8 質量對門架式橫梁固有角頻率的影響

由圖8可知，固有頻率隨密度增加而減小。因此，設備安裝后，橫梁的固有振動周期增大，對應的共振風速減小。

5 防治措施

通過以上分析可知，受迫振動的振幅主要受固有頻率、激勵頻率和阻尼3個因素影響，為減少橫梁振動可考慮下列3種措施。

5.1 提高固有頻率

固有頻率與鋼管外徑成正比，與跨徑平方成反比。通常跨徑無法減小，增加鋼管外徑不經濟。因此，可將單鋼管橫梁結構改為雙鋼管桁架結構來增加結構剛度。

5.2 增加阻尼

參考橋梁設計方法，增設橫向拉索或阻尼設置[6]；參考汽車行業，在梁上敷設約束阻尼層，通過振動時兩個表面層的相對位移增加阻尼[8]。

5.3 改善氣動外形

通過優化截面形狀、改變表面粗糙度，或在表面設置螺旋線，達到抑制渦振的目的[2, 6, 9]。

6 結論

本文通過分析等截面直梁橫向振動，證明了智慧公路設備橫梁振動為風荷載下的駐波，進而建立了橫梁受迫振動振幅與固有頻率、外部激勵頻率和阻尼的數學關系。經計算發現橫梁固有頻率與鋼管外徑成正比，與跨徑的平方成反比，隨設備質量增加而減小。通過風荷載分析證實設備橫梁的振動頻率與風在橫梁處繞流時的旋渦脫落頻率一致，當脫落頻率與橫梁固有頻率接近時，橫梁將發生大幅振動。增大結構剛度、增加阻尼或改善結構氣動外形能抑制橫梁振動。