串聯輸水渠系控制解耦算法優化與仿真

管光華，劉王嘉儀

串聯輸水渠系控制解耦算法優化與仿真

管光華，劉王嘉儀

（武漢大學水資源與水電工程科學國家重點實驗室，武漢 430072）

串聯輸水渠系耦合特性表現為針對單一渠池設計的控制器串聯使用后控制性能較差。解耦算法可在一定程度上增強渠池的獨立控制性能。該研究針對基于比例-積分-微分（Proportional-Integral-Differential，PID）反饋控制的上游方向解耦算法提出優化方案，首先對控制解耦算法中的解耦系數的選取范圍進行驗證；其次針對相鄰渠池長度差異較大的情況，在算法中引入放大系數以提升解耦效果；最后通過對不同取水流量規模、渠道上下游運行流量減半的算例進行仿真分析，驗證優化方案的控制性能。結果表明：1）解耦系數的合理取值范圍為0.8～1.0；2）放大系數可選用相鄰渠池水面面積之比；3）當串聯渠系上下游設計過流能力差異較大時，放大系數的修正能顯著提升控制效果。該研究提出的優化解耦算法可應用于不同規模復雜渠道系統的解耦控制器設計，對于灌區及引調水工程輸水系統的智能化調度有一定參考價值，工程應用時建議結合具體渠道的特點，根據渠道的特性和用途綜合考慮系數的取值。

渠道；算法；優化；輸水渠系；控制解耦；下游常水位；放大系數；PID控制器

0 引 言

中國水資源總量豐富，但人均擁有量較低，且南北分布不均，南方較為豐富而北方較為匱乏[1]。農業用水作為中國用水占比最大的產業，消耗量達到全國總用水量的60%以上[2]。其中農田灌溉用水為農業用水的主體，占其總量的90%[3]。提高節水灌溉技術是降低農業用水量、節約水資源的有效途徑[4]，而在灌溉輸配水階段，提高渠道自動化運行水平和灌區調度管理水平是提高用水效率的重要方式之一。

由于渠道具有非線性、滯后性的特點，渠池之間耦合問題突出，即單個渠池取水會導致其上下游相鄰渠池的水位也下降，引發多個閘門啟閉作用疊加[5]，在上游水庫補償蓄量前的短時間內多個渠池的水位會低于目標水位[6-7]，導致系統運行失穩。反饋調節器作用于單個渠池進行分散控制時，渠池間的相互影響不可避免，水位偏差增大，穩定時間延長，系統更加不穩定[8]，不利于灌溉用水的合理輸配和輸水渠系自動化控制。解耦可減小相鄰渠池的相互影響，在一定程度上實現單個渠池獨立調節，使渠道控制更加靈活和準確。

國內外學者對于解耦問題已有較多研究，Schuurmans[8-9]提出分別針對上、下游方向的Decoupler Ⅰ、Decoupler Ⅱ解耦結構，其以閘門開度為控制變量，并得到多位學者的驗證[10]；Acharya 等[11]提出將控制變量設為流量；Clemmens等[12]提出在比例-積分（Proportional-Integral，PI）控制器中引入滯后參數（lag），在反饋調節中考慮水波傳遞的滯后時間以盡快調節水位；上述提及的解耦方法均為在PI控制器的基礎上加入解耦環節；Malaterre[13]則以狀態空間為基礎，提出渠道的線性二次最優控制算法，在建模時考慮渠池之間的耦合，同樣實現解耦；Zhong等[14]證明優化的線性二次最優控制算法解耦效果明顯；崔巍等[15]基于水位-流量串級控制，提出僅需對上游方向解耦的PI反饋解耦控制算法，對于非線性強、滯后明顯的渠道來說較為有效。

已有研究表明，加入解耦器的分散控制器較其他方式控制效果更佳[16]，各閉環控制之間相互影響較低。且在針對單一渠池的分散控制器中加入解耦環節，省去了建立狀態空間方程的復雜建模及控制器求解。故崔巍等[15]提出的PI反饋解耦控制算法更為方便。然而，此算法目前仍存在不足：其針對相鄰渠池長度、運行流量相差較大的情況研究較缺乏，而此種情況常見于灌區渠道。本文在PI反饋解耦控制算法的基礎上，針對上游渠池長度大于下游渠池長度的情況添加放大系數，通過仿真模擬的方式，分析改進后的算法對控制效果的改善程度，并驗證其在不同工程情況下的適用性，以期為渠道控制解耦問題提供借鑒。

1 渠系控制與解耦算法優化

1.1 渠系控制方法

基于經典控制理論中應用廣泛的比例-積分-微分（Proportional-Integral-Differential，PID）反饋算法（如圖1所示）進行渠系控制。PID反饋算法由比例環節、積分環節、微分環節組成。比例環節主要用來減小水位偏差，積分環節用于消除閘門控制的殘差，微分環節用于加快閘門動作，減小穩定時間[17-19]。

PID反饋算法表達式標準方程[19]如式（1），若不考慮微分環節即為PI控制：

式中()為時刻的控制器輸出，即閘門的開度增量，m； K為比例系數；K為積分系數；K為微分系數。

崔巍等[20]曾提出水位-流量串級控制的方法，運用以流量為控制變量的PI控制。這種控制方法可使渠系靈活啟閉閘門以減小過閘流量偏差。基于此方法，下游方向的擾動被有效隔絕。

本文參照上述控制方法，僅針對上游方向的解耦算法進行改進，以彌補當前控制解耦算法的不足。

1.2 解耦算法優化

PID反饋控制是對擾動造成的偏差進行微調，這是僅針對于單一渠池的控制；解耦則協調相鄰渠池的閘門動作[20]，以降低渠池間的相互影響，保證在按時定量輸水的前提下盡快維持系統的穩定性。

在輸水渠系中，崔巍等[15,21]提出用以下方法對相鄰渠池進行解耦：將下游渠池的反饋流量，以一定權重（解耦系數K）傳遞至上游的反饋流量中，即將下游因水位偏差產生的調節量，納入上游渠池的調節控制中。將解耦流量逐渠池向上游傳遞，進而完成整個系統的解耦。加入解耦環節后，各閘門反饋控制算法如下[21]：

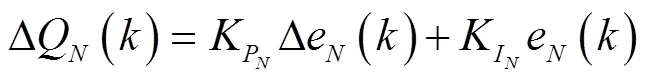
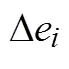
研究表明上述解耦系數取0.8～1.0較為合適[15,21]，但這僅適用于相鄰渠池長度差異不大或上游渠池短于下游渠池的情況；當上游渠池比下游渠池長時，下游渠池取水時上游仍會出現較大水位偏差。為了增大解耦程度，降低長度差異較大渠池之間的相互影響，本文提出在解耦系數前乘以放大系數，表達式如下：

對于解耦放大系數的取值，有以下初步分析：

1）由于取水后上游渠池將進行蓄量補償，下游常水位運行時，水面線以下游水位為支點轉動抬升[22]，反饋流量由渠池下游水位偏差決定，K的取值可能和這2個參數相關；

2）在實際渠道中，補償的真實蓄量較難確定，且緩坡渠道中水面線可視作水平抬升，故近似用補償蓄量與水位偏差的比值，即渠池的水面面積探究放大系數K取值的規律；

3）對于運行流量、斷面尺寸沿程無明顯變化的渠道，水面面積與渠池長度從研究角度來看是等價的；而對于上下游渠池流量、斷面變化較大的渠道，則需在二者之間選取更加合適的參數作為放大系數K的參考。

結合以上理論分析和仿真的可行性，本文選取渠道下游常水位運行時的水面面積作為研究對象，對放大系數的取值進行分析。

1.3 綜合控制性能指標

衡量系統控制性能不應以單一指標的最優性能為判別依據，而是以若干指標進行綜合比較以均衡控制效果。本文選取穩定時間t、絕對值誤差積分（Integral of Absolute Error，IAE）、絕對流量變化積分（Integral of Absolute Flow Change，IAQ）分別從時間、水位、流量這3個要素全面衡量系統的控制性能，其中t衡量系統穩定的快慢，其穩定狀態的判斷標準為連續3 h內閘門開度變化累計小于0.01 m且控制點水位偏差在目標水位的2%以內；IAE、IAQ分別衡量在過渡過程中水位波動的累積和系統對流量的控制能力[23]，其表達式分別如下：

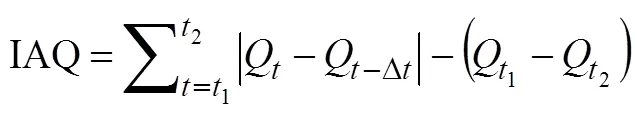
式中?為采樣時間步長，s；為系統仿真總時長，s；1、2分別為流量初始變化和最終穩定的時刻；Q為時刻過閘流量，m3/s。

管光華等[24]曾針對渠道自動化控制提出無量綱的綜合性能指標（GI），公式如下：

式中IAE為水位絕對值誤差積分，無量綱；k、NIAQ為去量綱的穩定時間、和絕對流量變化積分；為經驗系數，當流量、水位、穩定時間權重一致時=1。

解耦可降低因下游渠池分水帶來的水位偏差，但同時閘門動作量也會增加，本文衡量系統控制性能時側重解耦后對水位偏差的改善幅度，同時以對流量的控制能力作為輔助衡量指標，約束閘門動作量在適度的范圍內。本文對同一工程算例進行綜合指標對比，故不需對參數進行無量綱化，且增大水位偏差的權重以重視其改善幅度。保留式（7）格式，將變量修改為有量綱形式，適用于本文研究的綜合指標GI如式（8）所示，GI越小表示控制性能越好。

式中t為系統穩定時間，h；IAQ為絕對流量變化積分，m3/s。

IAE放大至和IAQ同量級進行計算。因側重水位偏差的改善幅度，將式（7）中IAE的指數放大至3。

1.4 仿真試驗

本文選取3個在渠池長度、取水流量、斷面尺寸方面差異較大的工程實例，在其基礎上進行合理修改作為不同工況的仿真算例。渠道A取自甘肅省疏勒河灌溉渠系；渠道B取自美國土木工程師學會（The American Society of Civil Engineers，ASCE）推薦的ASCE測試渠系；渠道C取自山東省麻灣灌溉渠系。在加入解耦環節前已將PI控制器中的參數P、I調節至系統振蕩較小、過渡較平穩的狀態，不同算例取值不同，在此不加贅述。并且研究過程中不改變其取值，對比解耦前后的控制性能變化。各算例渠池整體仿真總時長1 440 min，時間步長10 min，計算斷面間隔50 m。分水口取水時間360 min，與下游節制閘距離100 m，計算斷面間隔 10 m，其中分水口的分水流量線性增大。

2 結果與分析

2.1 基礎解耦系數取值

選取渠道A和渠道B的相鄰2渠池分析基礎解耦系數K的適宜取值，具體參數見表1。（注：不同算例選取2個渠道中，2個不同的相鄰渠池仿真，故分別展示每個算例中選取的渠池，不作統一展示。）

在取水時段內下游渠池的分水口進行取水，探究上游渠池受到下游渠池的影響程度，與加入解耦算法后的控制器對比控制效果，驗證已有研究在向上游方向解耦時，對基礎解耦系數K建議取值的合理性。由表2和圖2可知：1）增加解耦環節后，控制性能有顯著的改善；在0.6～1.0范圍內，隨著解耦系數的增大，水位誤差減小，閘門動作量在一定范圍內減小，但系數過大反而降低控制效果，且系數超過1.0出現超調，從渠道安全運行角度來說不適用；2）通過綜合指標的對比，取值在0.8～1.2之間時改善幅度較大，系數為1.0～1.2時解耦程度相對較高；3）通過圖2中曲線對比可知，系數大于1.0時出現明顯超調，即在過渡階段水位高于控制目標水位，從渠道安全運行角度來說應盡量避免。綜上，解耦系數在0.8～1.0之間較合適，驗證了崔巍等在研究中提出的解耦系數建議取值為0.8～1.0[15,21]。本文將固定采用K=0.8作為基礎解耦系數進行進一步研究。

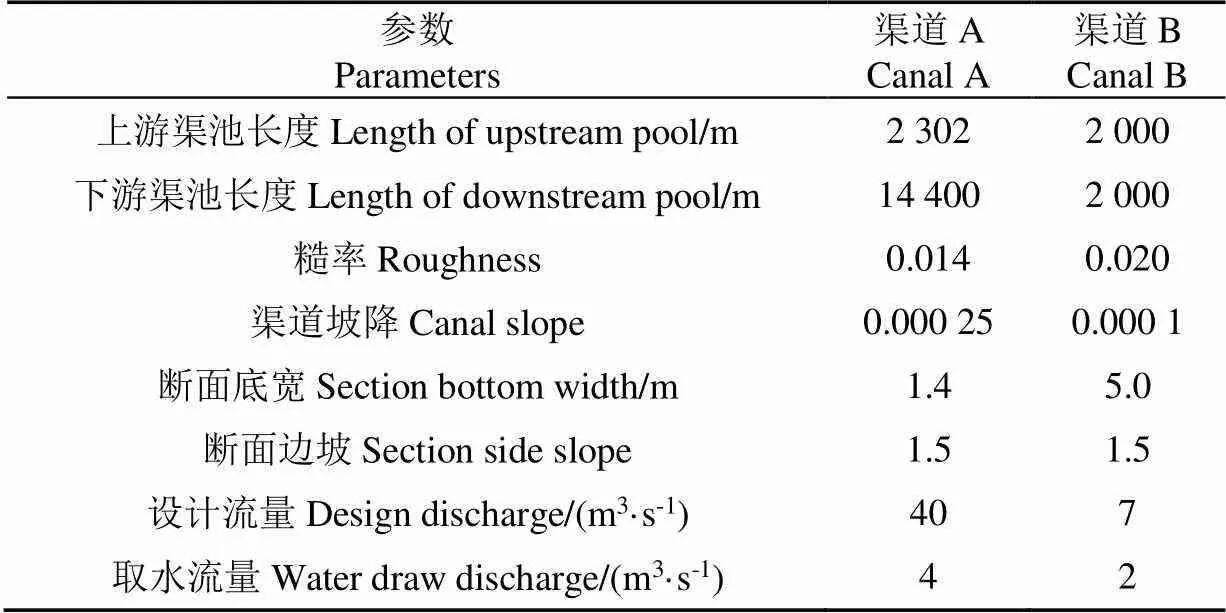
表1 渠道A、B部分渠池建模參數表

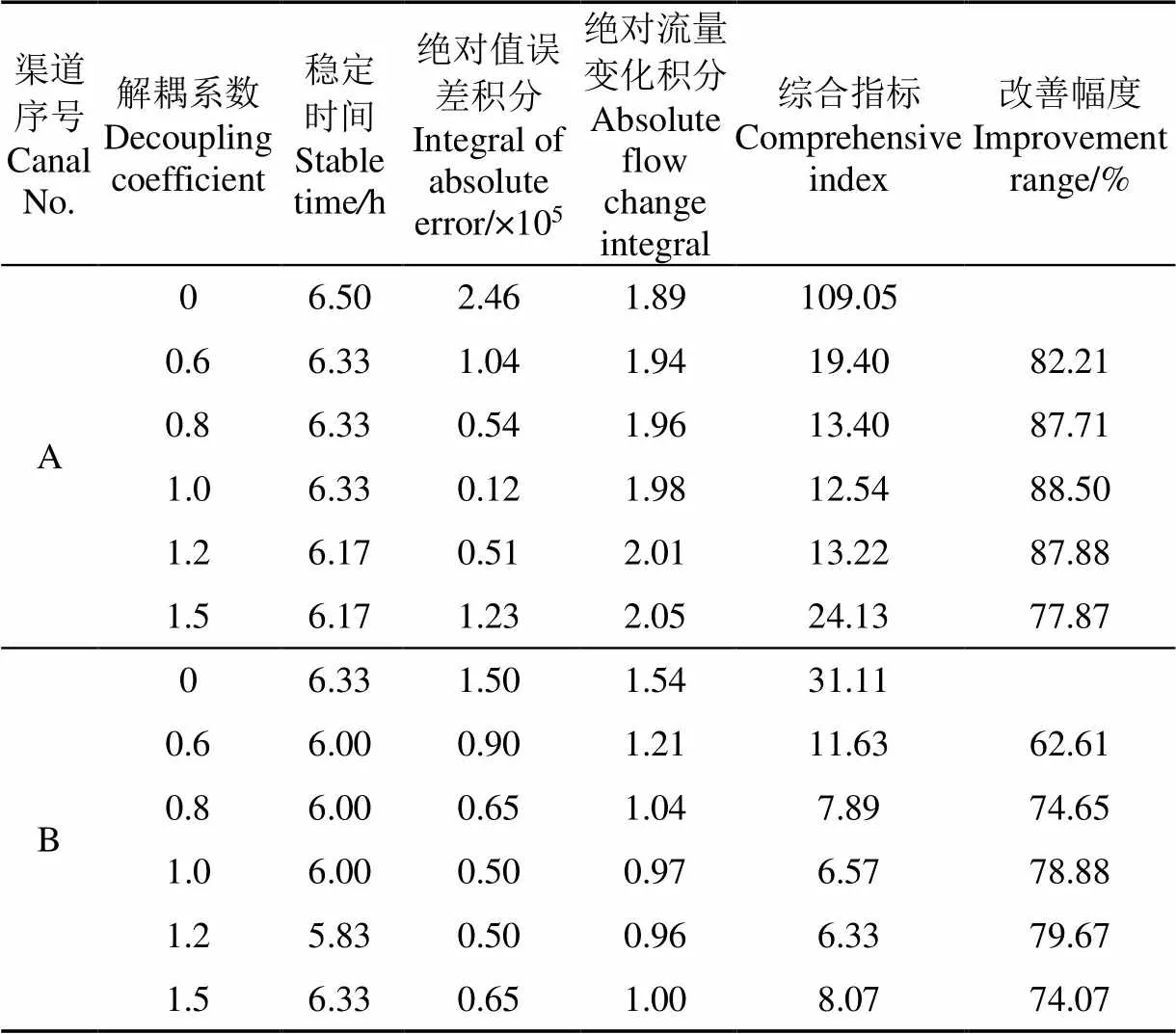
表2 渠道A、B上游渠池綜合指標對比

2.2 放大系數取值分析

選取渠道A進行仿真分析，渠道幾何參數見表1，為增大解耦前后的對比效果，取水流量增大到6 m3/s，其他設置同表1。采用上游方向解耦且上游渠池長度大于下游時，需在基礎解耦系數上乘以放大系數以優化算法，故在最下游渠池進行分水，研究上游長渠池的解耦效果。分別選取上下游渠池水面面積相差3.5、4.5、5.5倍進行對比分析，渠道整體建模如圖3所示。各情況的水位誤差線和綜合指標GI對比見圖4和表3。通過上下游水面面積相差3.5、4.5、5.5倍的3組數據可得K適宜的取值區間和面積差異的關系。

從圖4可以看出，解耦能降低渠池的水位誤差，略微縮短系統的穩定時間。加入放大系數后的算法能顯著提升解耦效果，在一定范圍內隨系數的增大，水位誤差和穩定時間減小，但繼續增大會帶來超調的問題，且水位誤差累積量增大。表3綜合指標對比更清楚地體現了放大系數的增大對控制性能的影響。隨著放大系數的增加，穩定時間、水位波動累積（t、IAE）均會經歷先減后增的過程，而流量變化積分（IAQ）明顯增加，說明閘門動作量增大，這與理論和經驗相符；對比GI可發現控制性能在系數增大過程中達到最優，與未解耦、未添加放大系數相比具有顯著提升。通過比較圖4改善幅度曲線可知，上下游水面面積3.5倍時，K較優區間[2.5，3.5]，相差4.5倍時，K較優區間為[4，5]，相差5.5倍時較優區間為[5，6]。綜合來看，放大系數取在上下游渠池水面面積差異倍數附近區間較合適，故總結公式如下：

K=αA/A且K>1 （9）

式中A為上游渠池水面面積，m2；A為下游渠池水面面積，m2；為經驗系數，可取0.9～1.1。

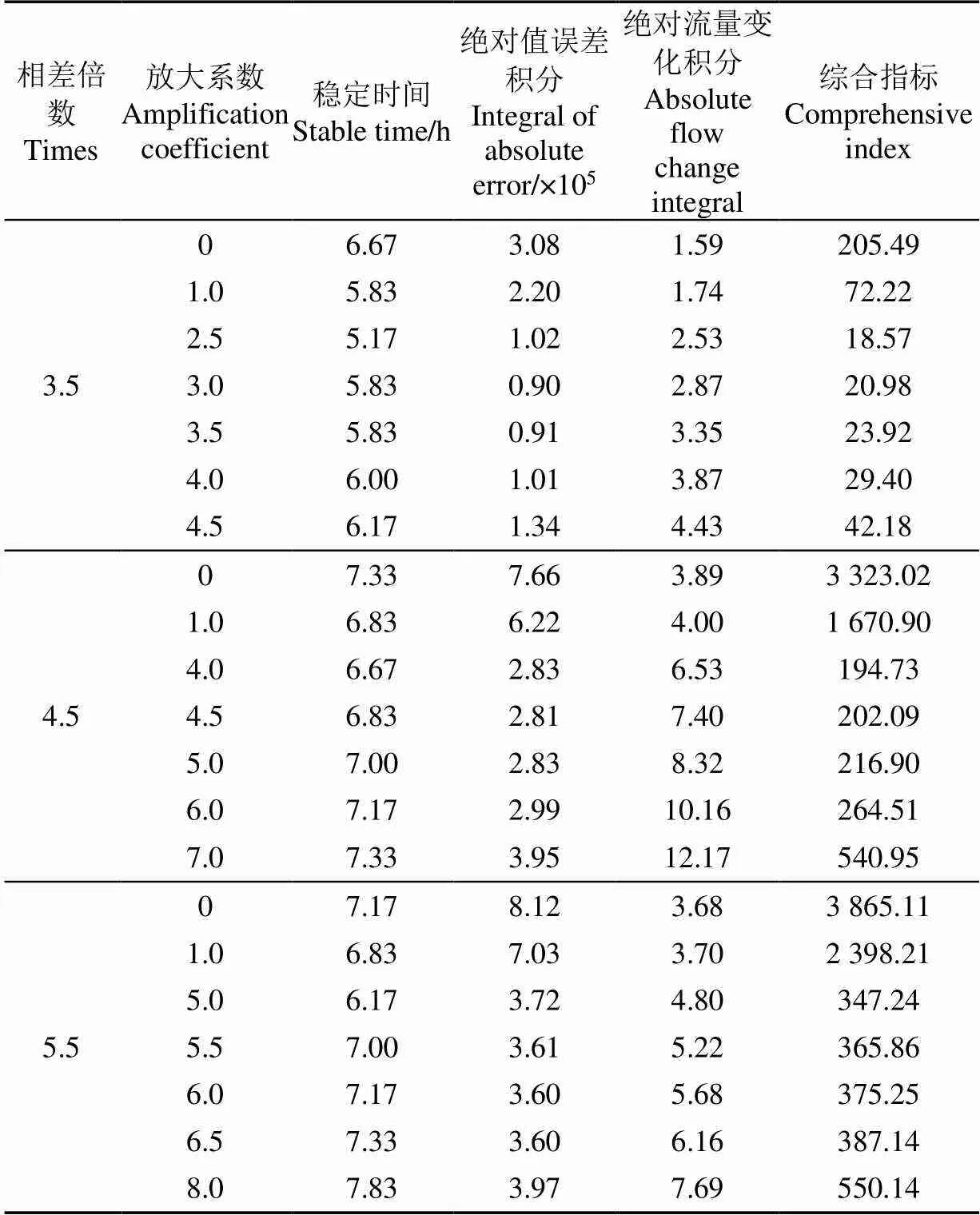
表3 上下游水面面積相差倍數不同時不同Ka下長渠池綜合指標對比

2.3 放大系數取值驗證

為了說明解耦算法中放大系數的普適性，在不同規模的渠系上均能達到解耦目的，選取灌區輸配水渠道普遍存在的2種情況對系數進行驗證。2種情況分別為取水流量差異較大的2渠道，同一渠道上下游渠池因支渠分水運行流量減半。

2.3.1 渠道系統規模差異

分別選取ASCE測試渠道（渠道B）和山東省麻灣灌溉渠系（渠道C）中的相鄰2渠池進行仿真分析，其中上游渠池長度大于下游渠池，在未取水時上下游水面面積分別相差1.6、1.8倍。渠道C分水流量是渠道B的9倍，取水流量規模差異較大，同時也說明渠道尺寸和過流能力相差較大。渠道相關參數和取水流量如表4所示。

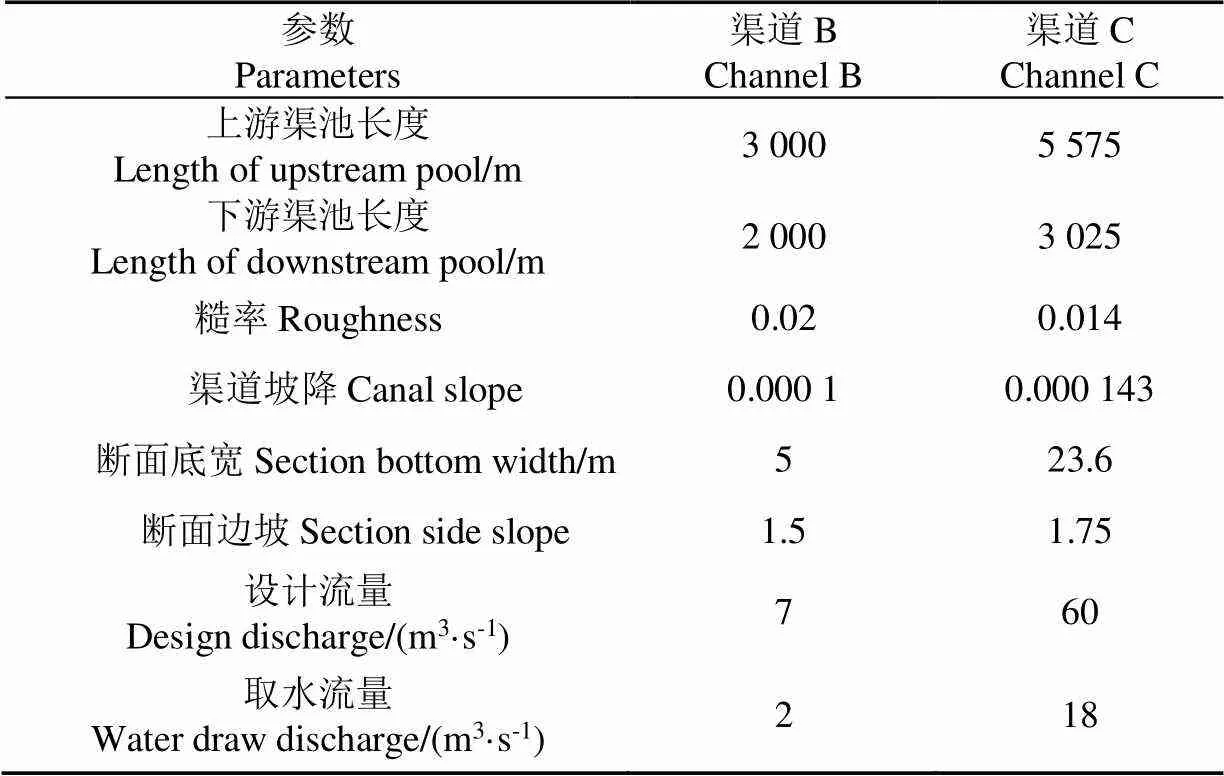
表4 渠道B、C部分渠池建模參數

對比圖5水位誤差線的走向和表5各指標的數據，可看出改善幅度的大小隨放大系數的增大呈現先增后減的趨勢，其中渠道C中K=2.5時，改善幅度出現負值?0.92%，代表與未解耦情況相比控制性能反而降低，這是由于系數增大解耦作用過度，導致閘門動作量和穩定時間過大。放大系數對系統穩定時間的影響取決于水位誤差和閘門動作量，故影響趨勢較為復雜。通過表5和圖5控制性能對比可知，K的適宜取值在渠道B、C中均在[1.5，2]內，同時分別取1.5、1.8時效果較優，驗證了上文中K的取值在上下游渠池水面面積相差倍數附近區間內這一結論。同時，通過渠道A、B、C這3個不同工程實例對比可知：1）相較于相鄰渠池長度相差較大的渠道A，相差較小的渠道B、C的K適宜區間更短，則式（9）中取值可更接近于1.0；2）反饋解耦算法的改善空間有限[25]，完美的解耦是不符合實際的。不同算例中解耦空間不同，并且和PID控制器參數設置有關，但針對此點本文不做詳細探究。

2.3.2 渠系間相鄰渠段幾何差異

輸水渠系通常會在干渠的側邊設若干支渠進行輸配水，故上下游渠池運行流量相差較大的現象時有發生。選取渠道A、B進行仿真，上游長渠池的運行流量是下游短渠池的2倍，下游渠池進行分水。由于算例中運行流量和斷面尺寸均不同，水面寬度沿程改變較大，故常水位運行時水面面積倍比和長度倍比相差較大，更符合灌區實際運行情況，進一步驗證式（9）的正確性。渠道相鄰長、短渠池建模參數和運行情況如表6。

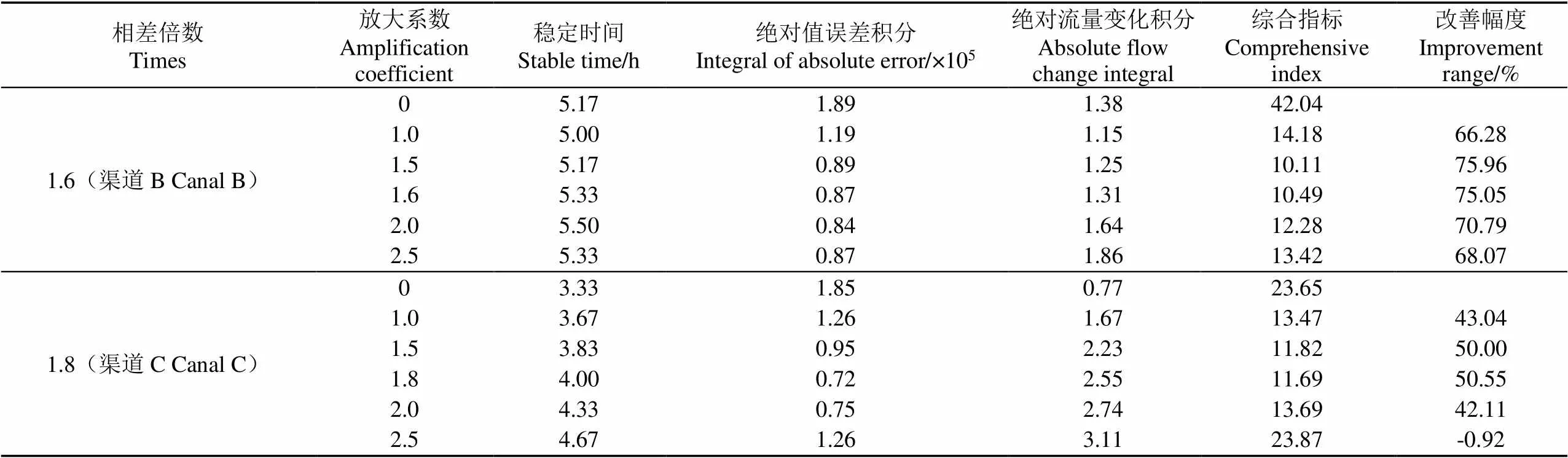
表5 上下游水面面積相差倍數不同時渠道B和C不同Ka下長渠池綜合指標對比

表6 渠道A、B上下游渠池參數

由表7和圖6對比可知，渠道A中K的適宜取值區間為[6，7]；渠道B中K的適宜取值區間為[2.5，3]。此時渠道A上下游渠池長度相差5倍，水面面積相差6.5倍；渠道B長度相差2倍，水面面積相差2.5倍，可知K更接近水面面積的倍比，驗證了以A/A作為K取值參考的合理性。同時驗證了添加放大系數后的解耦算法對于渠道運行流量減半的情況同樣具有顯著的解耦效果。

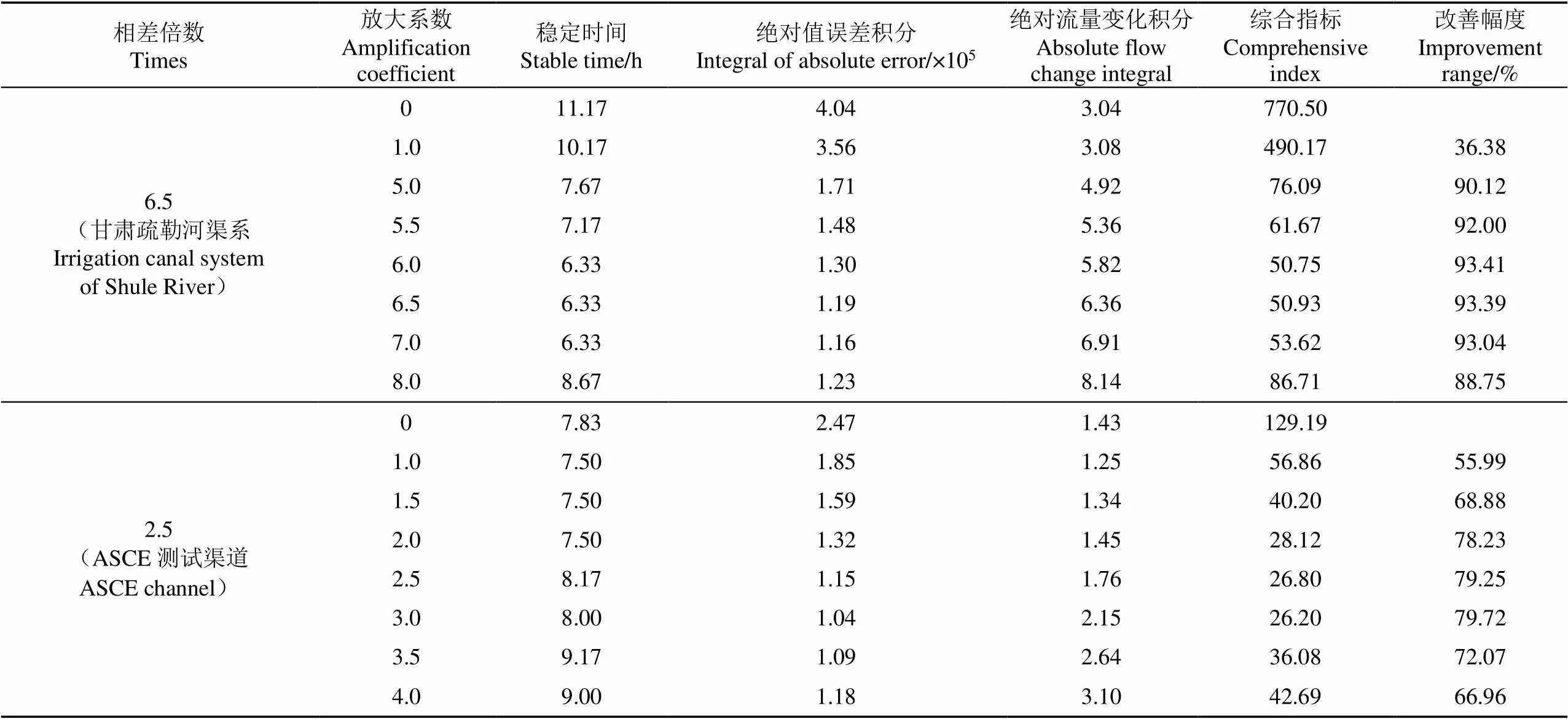
表7 上下游水面面積相差倍數不同時渠道A和B不同Ka下長渠池綜合指標對比

如多渠池系統要取得較大的整體性能改善，則每個渠池需根據其與下游渠池的水面面積比，選擇不同的放大系數進行解耦。當K在水面面積倍比附近選取時，渠道A（3渠池串聯）和渠道B（4渠池串聯）的整體改善幅度可達到58.40%和47.42%；相較于未引入放大系數的方案也分別有34.15%和13.19%的改善（具體工況設置和指標分析未在文中展示）。可以看出整體性能改善幅度比單一渠池小，這是因為實際工程中渠池長度多變，并且渠池之間的相互影響造成閘門動作量大大增加，但總體仍有明顯的改善。

3 討 論

由表3、5、7可知：在渠道A甘肅疏勒河灌渠中，各組工況解耦后改善幅度最大均能達到90%以上；渠道B為渠道斷面稍大的ASCE測試渠道，當相鄰渠池的運行流量差異和渠池長度倍比改變時，最大改善幅度也均能達到75%以上；而渠道C選取的麻灣渠道渠道斷面尺寸和設計流量較另外2個算例較大，改善幅度則相對較小，較優時僅有50%，可見解耦優化方案對不同渠道的性能提升程度是不同的。這是由于改善程度和系統的自動控制能力聯系緊密，且水力響應特性和渠道斷面及流量有關[26]。優化后的解耦算法無法完全消除渠池間的耦合關系，而對于規模越大的渠道，控制難度越大[27]，解耦效果就更加有限。此外，本文雖未對K和K的搭配效果做出詳細分析，但由于是對K的解耦效果進行放大，其配合效果一定程度上取決于K的取值是否合適，仿真結果同樣可證明此點。

渠道水面線可簡化為均勻流區和回水區，且回水區是基于閘前水位壅高，水波反射的水動力特征在低頻域內簡化的[9]，故其大小會影響相鄰渠池的耦合關系和解耦程度。但由于回水區的界限在實際渠道中較難確定，故本文選取下游常水位運行時的渠道水面面積作為近似的研究對象。但從工程應用角度來說，利用水面面積求放大系數的適宜取值區間有一定的復雜性和變化性，故在此分析采用渠池長度倍比作為參考指標的適用情況。如2.2節中渠道A設置的3種長度倍比分別為4、5、6倍，根據圖4可知，當K選取4、5、6時，其改善幅度和選取水面面積倍比3.5、4.5、5.5時，差值在2%以內，其降低幅度均在較小的范圍內，故對于實際工程而言在此情況下選取長度倍比為放大系數K是合理的，且應用更為簡單。但對于渠道沿程會進行大幅分水的工況，如2.3節中上下游運行流量相差一半：若選取相鄰渠池的長度倍比，根據表7可知，渠道A的K取5時，改善幅度相較于水面面積倍比的6.5，則相差3.27%，解耦效果降低得更多。文中疏勒河灌渠和麻灣干渠可代表規模不同的工程實例，尤其疏勒河沿程的流量和斷面尺寸相差較大，放大系數的取值更加貼近水面面積倍比，此類渠道建議選取水面面積作為參考指標，不建議以長度倍比代替。

目前輸水渠系的耦合問題對某些渠道的穩定運行顯著影響，進而影響輸配水的運行效率及配水效果。本文提出的解耦優化方案，能大幅降低因下游渠池取水對上游渠池造成的水位偏差，達到各渠池相對較優的控制效果，有利于實現各渠池的獨立控制。并且優化方案只需在原有解耦系數的基礎上添加放大系數，思路簡單、計算方便，對工程應用有一定參考價值和借鑒意義。但該優化方案仍存在局限性，輸水渠系一般支渠眾多，取水時段和取水流量不同，水力相應特征也不同[28]。供水系統中過水建筑物也同樣對耦合有所影響[29]，故對多條支渠分水、干支渠復雜銜接等情況的解耦優化仍有待研究。另外，解耦方式也可考慮通過自主學習達到自適應控制，和PID自適應調節參數類似[30]，根據渠道不同運行流量帶來的水面面積倍比的變化，調整放大系數的取值，更加精確迅速地對渠池的擾動做出響應，降低渠池間的耦合程度。

4 結 論

本文針對相鄰渠池長度、運行流量差異較大的解耦問題，在已有解耦算法中引入放大系數和基礎解耦系數相乘的優化方案，采用仿真分析的方式驗證放大系數選取的適宜區間，并選取不同輸水渠系實例驗證其合理性和適用性，證明其在實際工程控制解耦上的效果。研究得到以下結論：

1）驗證了上游方向解耦時，上游渠池長度小于下游渠池長度時，基礎解耦系數0.8～1.0適用；當上游渠池長度大于下游渠池長度時，則需引入放大系數進行優化。

2）提出了解耦放大系數，建議取值在渠道下游常水位運行時，相鄰渠池水面面積倍比的附近。加入放大系數后，水位誤差改善較明顯，系統穩定時間明顯減小，閘門動作量在可接受范圍內，控制性能的改善效果較為顯著，并提出計算放大系數的公式。

3）通過不同渠道取水規模差異較大、相同渠道上下游運行流量減半的工況對優化方案進行驗證，各工況下解耦效果均有顯著提升，在實際工程中有一定的普適性。

4）當渠道內運行流量和斷面尺寸沿程無明顯變化時，為方便工程應用可直接以長度倍比確定放大系數；反之，運行流量差異較大時，則最好以水面面積倍比確定。說明優化方案對于灌區渠道的大部分情況均適用。

[1] 吳普特，馮浩，牛文全，等. 中國用水結構發展態勢與節水對策分析[J]. 農業工程學報，2003，19(1)：1-6.

Wu Pute, Feng Hao, Niu Wenquan, et al. Analysis of development tendency of water distribution and water-saving strategies[J]. Transactions of the Chinese society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(1): 1-6. (in Chinese with English abstract)

[2] 倪文進. 中國農村水利發展狀況與科技需求[J]. 農業工程學報，2010，26(3)：1-8.

Ni Wenjin. Development and technology requirement of China rural water conservancy[J]. Transactions of the Chinese society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(3): 1-8. (in Chinese with English abstract)

[3] 范群芳，董增川，杜芙蓉. 農業用水和生活用水效率研究與探討[J]. 水利學報，2007，38(增刊1)：465-469.

Fan Qunfang, Dong Zengchuan, Du Furong. Study of agriculture water and life water use efficiency[J]. Journal of Hydraulic Engineering, 2007, 38(Supp.1): 465-469. (in Chinese with English abstract)

[4] 李慧，丁躍元，李原園，等. 新形勢下我國節水現狀及問題分析[J].南水北調與水利科技，2019，17(1)：202-208.

Li Hui, Ding Yueyuan, Li Yuanyuan, et al.Analysis of status quo and problems of water conservation in China in new situation[J]. South-to-North Water Transfers and Water Science & Technology, 2019, 17(1): 202-208. (in Chinese with English abstract)

[5] 崔巍，王長德. 調水工程運行最優控制研究[J]. 南水北調與水利科技，2007，5(2)：6-8，24.

Cui Wei, Wang Changde. Optimal control of water diversion projects[J]. South-to-North Water Transfers and Water Science & Technology, 2007, 5(2): 6-8, 24. (in Chinese with English abstract)

[6] 管光華，廖文俊，毛中豪，等. 大型輸水渠系蓄量非疊加非充分補償優化算法[J]. 華中科技大學學報：自然科學版，2019，47(9)：60-66.

Guan Guanghua, Liao Wenjun, Mao Zhonghao, et al. Optimization algorithm for non-superimposed inadequate volume compensation in large-scale water conveyance canal system[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2019, 47(9): 60-66. (in Chinese with English abstract)

[7] 管光華，廖文俊，毛中豪，等. 渠系前饋蓄量補償控制時滯參數算法比較與改進[J]. 農業工程學報，2018，34(24)：72-80.

Guan Guanghua, Liao Wenjun, Mao Zhonghao, et al. Comparison and improvement of time delay parameter algorithm for feedforward volume compensation control in canal system[J]. Transactions of the Chinese society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(24): 72-80. (in Chinese with English abstract)

[8] Schuurmans J. Control of Water Levels in Open-channels[D]. Netherlands: Delft University of Technol, 1997.

[9] Schuurmans J, Bosgra H, Brouwer R. Open-channel flow model approximation for controller design[J]. Applied Mathematical Modelling, 1995, 19(9): 525-530.

[10] Wahlin B T, Clemmens A J. Performance of historic downstream canal control algorithms on ASCE test canal 1[J]. Journal of Irrigation and Drainage Engineering, 2002, 128(6): 365-375.

[11] Acharya K D, Sau J, Sanfilippo F. Narmada project: Controlled volume concept[R]. France: Société du Canal de Provence, 1999: 122-127.

[12] Clemmens A J, Strand R J. Downstream-water-level control test results on the WM lateral canal[J]. Journal of Irrigation and Drainage Engineering, 2010, 136(7): 460-469.

[13] Malaterre P-O. Linear quadratic optimal controller for irrigation canals[J]. Journal of Irrigation and Drainage Engineering, 1998, 124(4): 187-194.

[14] Zhong K, Guan G H, Tian X, et al. Evaluating optimization objectives in linear quadratic control applied to open canal automation[J]. Journal of Water Resources Planning and Management, 2020, 146(11): 04020087-1-04020087-12.

[15] 崔巍，陳文學，郭曉晨，等. 明渠調水工程閘前常水位運行控制解耦研究[J]. 灌溉排水學報，2009，28(6)：9-13，29.

Cui Wei, Chen Wenxue, Guo Xiaochen, et al. Research on decoupling of constant downstream depth operation of canal[J]. Journal of Irrigation and Drainage, 2009, 28(6): 9-13,29. (in Chinese with English abstract)

[16] Hanuma N R, Kumar D, Gopikrishna R P V. Improved centralised control system for rejection of loop interaction in coupled tank system[J]. Indian Chemical Engineer, 2019, 62(2): 118-137.

[17] Wahlin, B T, Clemmens A J. Automatic downstream water-Level feedback control[J]. Journal of Irrigation and Drainage Engineering, 2006, 132(3): 198-207.

[18] van Overloop P J, Schuurmans J, Brouwer R, et al. Multiple-model optimization of proportional integral controllers on canals[J]. Journal of Irrigation and Drainage Engineering, 2005, 131(2): 190-196.

[19] 美國內務部墾務局著. 現代灌區自動化管理技術實用手冊[M]. 高占義，謝崇寶，程先軍，譯. 北京：中國水利水電出版社，2004.

[20] 崔巍，陳文學，姚雄，等. 大型輸水明渠運行控制模式研究[J]. 南水北調與水利科技，2009，7(5)：6-10，19.

Cui Wei, Chen Wenxue, Yao Xiong, et al. Research on canal control of large scale water transfer Project[J]. South-to-North Water Transfers and Water Science & Technology, 2009, 7(5): 6-10, 19. (in Chinese with English abstract)

[21] 崔巍，陳文學，郭曉晨.明渠閘前常水位運行控制解耦試驗研究[J]. 水力發電學報，2012，31(6)：115-119，125.

Cui Wei, Chen Wenxue, Guo Xiaochen. Experimental study on decoupling algorithm for canal operation at constant downstream depth[J]. Journal of Hydroelectric Engineering, 2012, 31(6): 115-119, 125. (in Chinese with English abstract)

[22] 崔巍，陳文學，郭曉晨. 明渠運行控制模型研究進展[J]. 南水北調與水利科技，2009，7(4)：5-9.

Cui Wei, Chen Wenxue, Guo Xiaochen. Progress in research on canal control models[J]. South-to-North Water Transfers and Water Science & Technology, 2009, 7(4): 5-9. (in Chinese with English abstract)

[23] Clemmens A J, Kacerek T F, Grawitz B, et al. Test cases for canal control algorithms[J]. Journal of Irrigation and Drainage Engineering, 1998, 124(1): 23-30.

[24] 管光華，鐘錁，廖文俊，等. 基于無量綱性能指標的渠系控制器參數優化[J]. 農業工程學報，2018，34(7)：90-99.

Guan Guanghua, Zhong Ke, Liao Wenjun, et al. Optimization of controller parameters based on nondimensional performance indicators for canal systems[J]. Transactions of the Chinese society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 90-99. (in Chinese with English abstract)

[25] 閔娟，黃之初. 多變量解耦控制方法[J]. 控制工程，2005，12(增刊2)：125-127.

Min Juan, Huang Zhichu. Methods of multivariable decoupling control[J]. Control Engineering of China, 2005, 12(Supp.2): 125-127. (in Chinese with English abstract)

[26] 穆祥鵬，陳文學，崔巍，等. 南水北調中線工程渠道敏感性研究[J]. 水力發電學報，2012，31(6)：109-114.

Mu Xiangpeng, Chen Wenxue, Cui Wei, et al. Study on hydraulic response sensitivity of canal pools of the middle route of South-to-North Water Diversion Project[J]. Journal of Hydroelectric Engineering, 2012, 31(6): 109-114. (in Chinese with English abstract)

[27] 范杰，王長德，管光華，等. 渠道非恒定流水力學響應研究[J]. 水科學進展，2006，17(1)：55-60.

Fan Jie, Wang Changde, Guan Guanghua, et al. Study on the hydraulic reaction of unsteady flows in open channel[J]. Advances in Water Science, 2006, 17(1): 55-60. (in Chinese with English abstract)

[28] 李抗彬，沈冰，李智錄，等. 基于非恒定水流模擬的灌區明渠水力響應特征分析[J]. 農業工程學報，2015，31(10)：107-114.

Li Kangbin, Shen Bing, Li Zhilu, et al. Open channel hydraulic response characteristics in irrigation area based on unsteady flow simulation analysis[J]. Transactions of the Chinese society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(10): 107-114. (in Chinese with English abstract)

[29] Mao Z H, Guan G H, Yang Z H, et al. Linear model of water movements for large-scale inverted siphon in water distribution system[J]. Journal of Hydroinformatics, 2019, 21(6): 1048-1063.

[30] 韓延成，高學平. 基于RBF人工神經網絡的下游常水位自適應渠道輸水控制研究[J]. 西北農林科技大學學報：自然科學版，2007，35(8)：202-206.

Han Yancheng, Gao Xueping. Research of self-adapting canal downstream constant level control based on RBF neural network[J]. Journal of Northwest A & F University: Natural Science Edition, 2007, 35(8): 202-206. (in Chinese with English abstract)

Optimization and simulation of decoupling algorithm for cascade drainage system control

Guan Guanghua, Liu Wangjiayi

(,,430072,)

Coupling characteristics of a series channel system refers that the regulation action of a single control gate can affect the water level of adjacent pools in upstream/downstream reaches. Without decoupling, there is often a dramatic decline in the performance of the control system, even instability in the optimal controller for a single channel pool. In particular, the coupling effect is more complex, because there are significant differences in the length and capacity of adjacent channels in various irrigation districts of China. Decoupling can allow the pools to run independently of channel control, making it easier to change the individual channel. However, it is still lacking in the design principle of decoupling coefficient in complex canal systems with different lengths and scales. In this study, an optimization was proposed for decoupling algorithm in the upstream direction using Proportional-Integral-Differential (PID) feedback control. Firstly, an efficient range was determined for the decoupling coefficient. Secondly, an amplification factor was introduced to improve the decoupling effect in various lengths of adjacent channels. Finally, a simulation was carried out under different water intake flows and geometric structures between the upper and lower reaches of the channel. Three engineering examples were also selected with different decoupling amplitude to verify the simulation. The results show that the optimization scheme presented a significant improvement in the control performance. The improved range of system increased first and then decreased, with the addition of amplification factor. There was also an excellent enhancement of coefficient interval with a gentle change of the improved range in the middle, indicating that the reasonable value range of amplification factor. Specifically, 1) the specific range of basic decoupling coefficient should be between 0.8 and 1.0. 2) A calculation formula was proposed, while the amplification factor was selected in the area near the ratio of water surface area of adjacent channels and pools. 3) The selection and correction of the amplification factor significantly improved the control performance, when the upstream and downstream designs of a series channel system differed greatly in the flow capacity. 4) The amplification factor was directly determined by the length ratio for the convenience of engineering application when there was no obvious change in the flow rate and section size in the channel. Whereas, it was best to determine the ratio of water surface area when the operating flow varied greatly. Furthermore, the optimized decoupling adjusted the value of amplification factor, according to the change of water surface area ratio caused by different channel flow, responding more accurately and rapidly to the disturbance of channel pool, while reducing the degree of coupling between the channels. Consequently, the algorithm can be applied to the decoupling controller design in the complex channel systems in different scales, further to realize the independent control of drainage pools. The finding can provide a sound reference for the intelligent scheduling of water transmission systems in the irrigation district and water diversion projects. More importantly, it can be suggested to consider the characteristics of specific channels for the optimized coefficient, according to the response characteristics and application of channels in engineering applications.

canals; algorithms; optimization; drainage system; control decoupling; downstream constant water level; amplification factor; PID controller

10.11975/j.issn.1002-6819.2021.15.009

S274.2; TV91

A

1002-6819(2021)-15-0068-10

管光華，劉王嘉儀. 串聯輸水渠系控制解耦算法優化與仿真[J]. 農業工程學報，2021，37(15)：68-77.doi：10.11975/j.issn.1002-6819.2021.15.009 http://www.tcsae.org

Guan Guanghua, Liu Wangjiayi. Optimization and simulation of decoupling algorithm for cascade drainage system control[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(15): 68-77. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.15.009 http://www.tcsae.org

2021-03-30

2021-06-10

國家自然科學基金項目（51979202，51009108）

管光華，博士，副教授，研究方向為渠道系統自動化運行調度理論與技術，灌區量水理論與方法，灌排工程新結構。Email：GGH@whu.edu.cn

中國農業工程學會會員：管光華（E041700033M）