基于多尺度法的船舶橫搖運動特性分析
李敏,曹樂,沈頡
(201620 上海市 上海工程技術大學 電子電氣工程學院)
0 引言
船舶在航行過程中會受波浪等因素影響引發大幅橫搖運動[1],導致船上人員無法正常作業甚至造成傾覆事故,帶來嚴重的經濟損失[2],準確分析和預測船舶橫搖運動狀態具有重要的理論和現實意義,也吸引了眾多學者的廣泛關注。Oh[3]等人采用縱搖與橫搖運動耦合的方法研究參數橫搖現象。研究發現,當波浪頻率為船舶橫搖固有頻率的2 倍時,最易發生參數橫搖共振現象。同時,當波浪頻率接近船舶橫搖固有頻率時將會引起較大的橫搖幅度,使船舶陷入不穩定狀態[4-5];Obreja[6]等人建立了一類垂蕩、橫搖和縱搖的耦合方程,系統分析了參數橫搖現象。其中,平均非線性方法的發展和應用增大了預測船舶參數橫搖的可能性,為船舶的運動分析和結構設計提供了實用價值。現有數值仿真工具[7-8]可根據工況下對應的參數直接預測并模擬船舶的運動狀態,判斷其是否處于參數橫搖狀態。
船舶穩定性是指其在靜水和波浪中保持垂直漂浮位置的能力,也是船舶結構最基本的性能之一,保證了船舶航行過程中的安全性能[9]。Moideen[10]等人分析了Mathieu 不穩定圖譜與船舶參量之間的關系,給出不同航速下船舶穩定的判斷條件,并對常規波下的初穩心高度進行了估算;Himeno[11]分析了阻尼對參數橫搖運動的影響,指出阻尼越大越不容易發生橫搖運動;戎海武[12]等人應用改進的變形參數法對Mathieu 方程邊界值進行求解,但精度仍需進一步提高;徐亞杰[13]針對船舶的轉動慣量進行測量,從而對船舶的橫搖運動進行仿真分析,但仿真過程較為復雜。
本文基于船舶結構建立橫搖運動動力學方程,采用多尺度法給出近似解析解的表達形式,同時利用Hill 行列式結合運動方程特點繪制船舶不穩定參數圖譜,并定性分析了不同阻尼下的船舶狀態。基于船舶橫搖角的解析解,分析不同小參數下橫搖運動的時歷變化及相圖的收斂性,從而判斷船舶穩定性,進一步研究其對船舶橫搖運動的影響。另外,對船舶參數不穩定圖譜中給定點的橫搖運動進行預測,并通過增加阻尼項分析其對船舶恢復至穩定狀態的影響程度。
1 船舶運動學分析
1.1 模型建立
復雜海況下,船舶極易發生垂蕩-橫搖耦合運動,即出現參數共振現象。不同海況下的波浪表征出不同的運動學特性,本文著重分析單頻波浪影響下船舶的橫搖運動響應,變化情況如圖1表示。其中,M0為船舶初穩心;GM0對應船舶在靜水中的初穩心高度;B0為靜水中的浮心位置;GZ 表示恢復力矩。受海浪因素影響,船舶浮心由B0偏移到B1,產生橫搖角φ,φ可表示為以M0為圓心,M0B0為半徑的圓弧B0B1所對應的夾角。船舶初穩心高度表示為
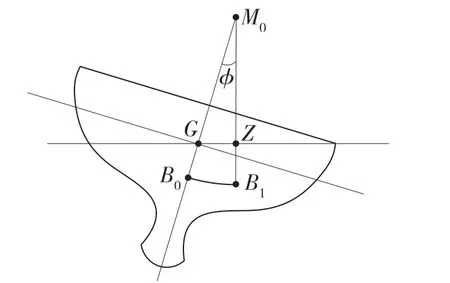
圖1 船舶橫搖運動簡圖Fig.1 Schematic chart of ship roll motion
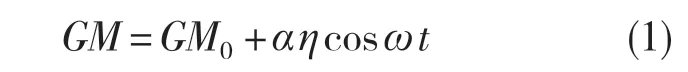
式中:α——單位垂蕩運動引起的GM 變化;η——垂蕩運動隨橫搖運動恢復力剛度的變化程度;ω——船舶垂蕩運動頻率。
船舶橫搖運動微分方程[14]可表示為
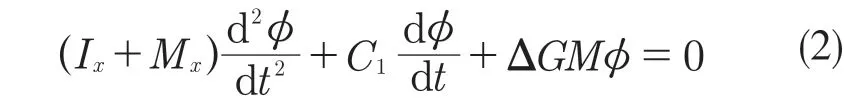
式中:Ix——橫搖慣性矩;Mx——橫搖附加質量;C1——線性阻尼系數;Δ——排水量。
令τ=ωt,將式(1)代入式(2),并進行無量綱化處理可得

1.2 橫搖運動方程的求解
本文采用多尺度法求解船舶橫搖運動方程,其主要思想是將關于時間τ的高階微分方程轉換為多重尺度變量Tn的低階偏微分方程進行求解,能夠克服攝動方法一次近似求解方法精度低、二次近似求解方法復雜度高的缺點。
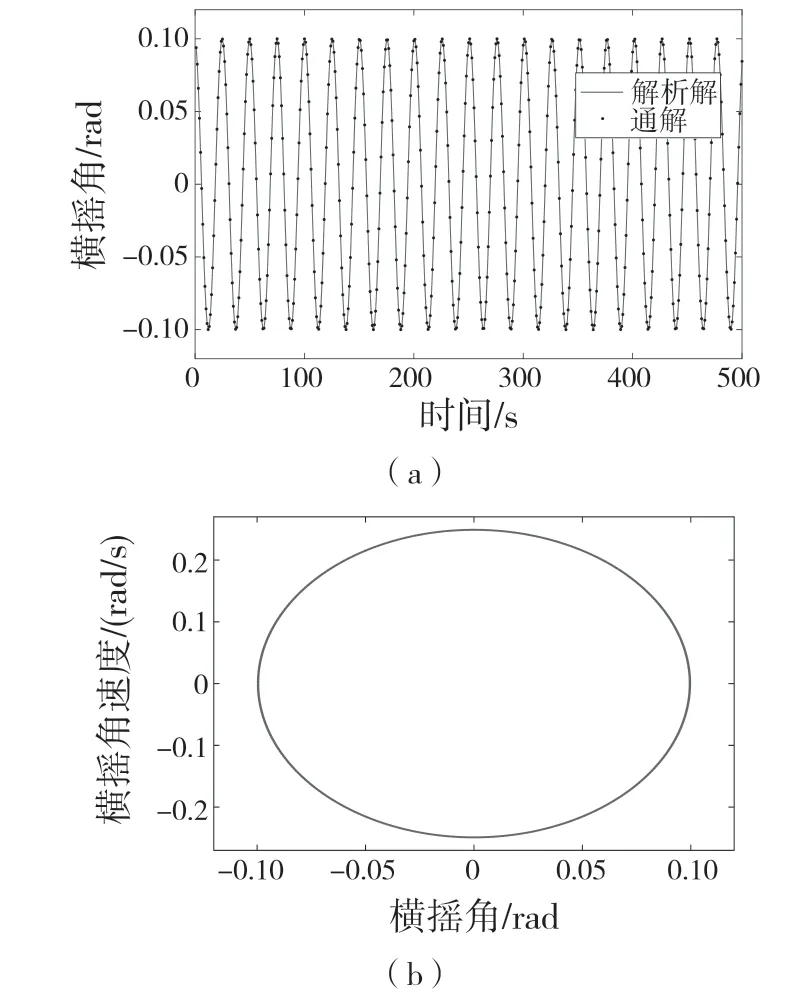
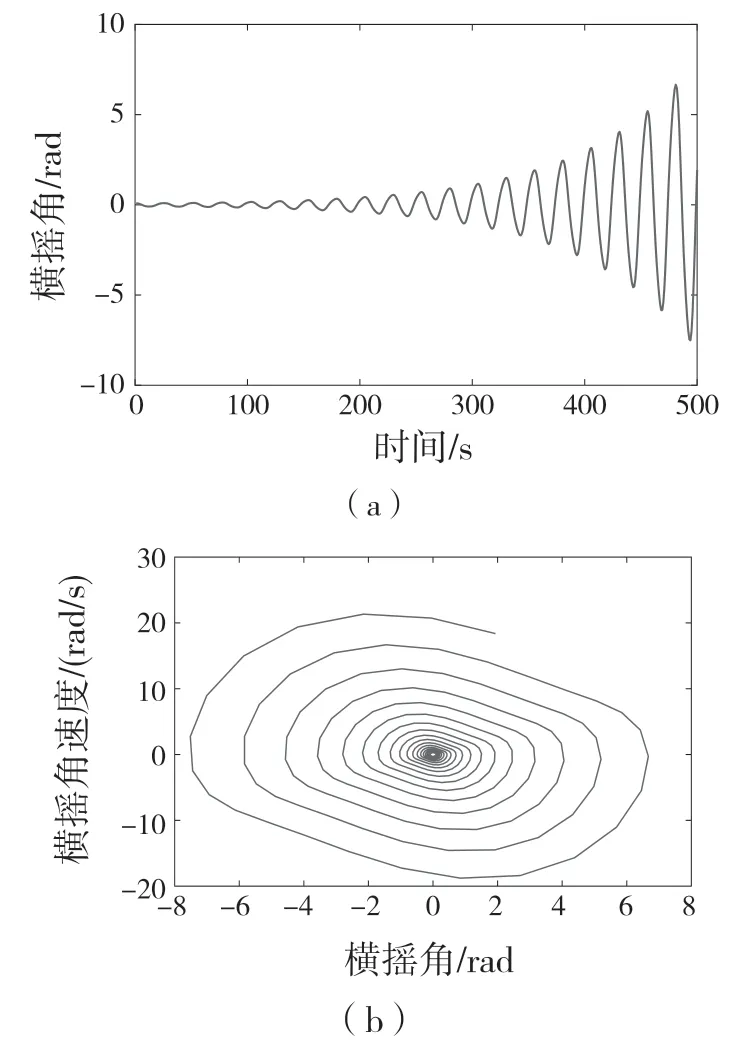
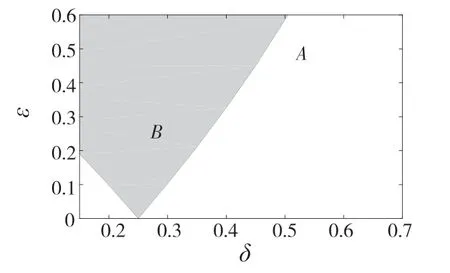
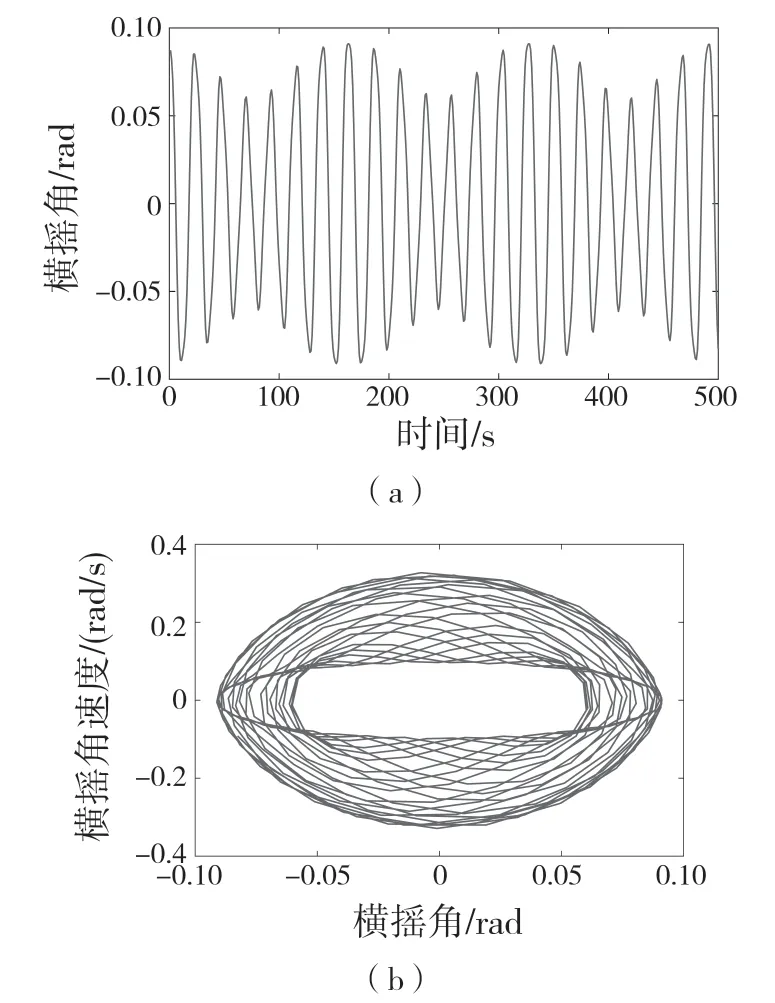
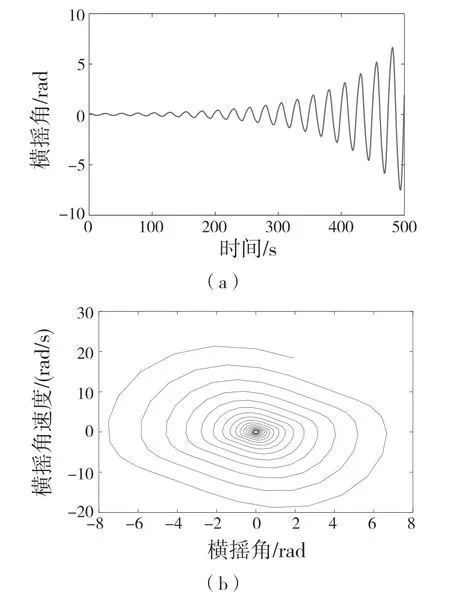
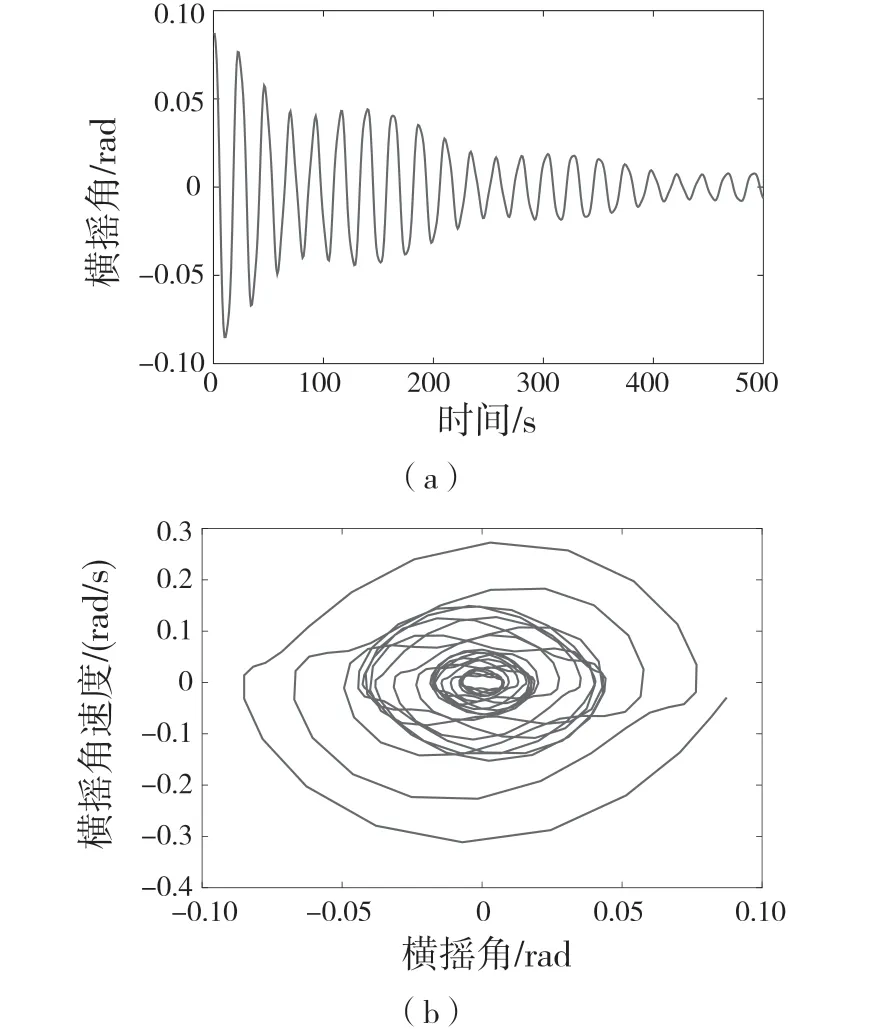
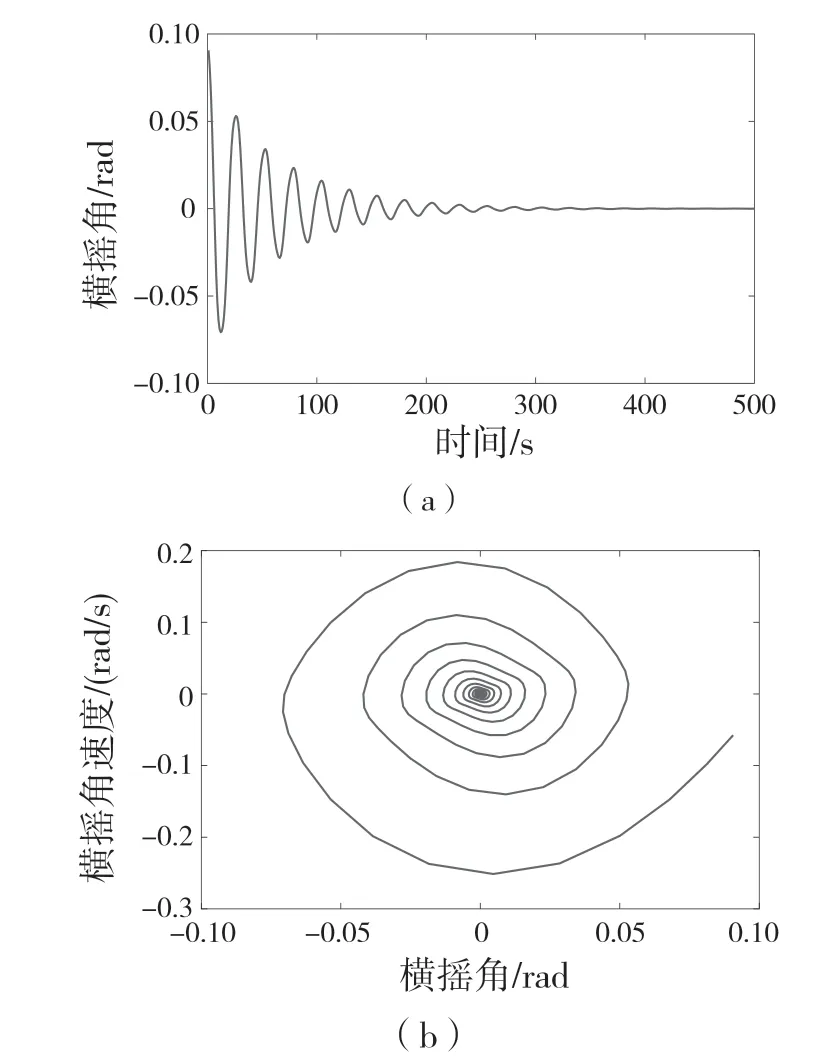
首先,對式(3)引入小參數r,取值范圍為0 式中:σ——頻率調諧參數,表示垂蕩頻率與2倍橫搖固有頻率的相關程度。 將式(4)代入式(3)中,可得 設式(3)通解的形式 式中:T0=τ;T1=rτ;T2=r2τ。 定義微分算子: 將式(6)—式(8)代入式(5),根據所得偏微分方程按r 的階次進行整理,可得 設式(9)解的形式為 將式(12)代入到式(10) 式中:cc——前面幾項的共軛。 為了得到一致有效的展開式,消除方程(13)中的長期項,需滿足以下條件: 消除長期項后,式(10)表示為 設式(15)中解的形式可表示為 將式(12)和式(16)代入式(11),可得 消除式(17)中的長期項,可得 根據式(14)和式(18)可分別解得 將A 表示成極坐標形式: 同時,將式(19)、式(20)和式(21)分別代入式(22)中并分離其實部與虛部,可得 因此,式(3)近似解析解的表達形式為 本小節利用Hill 行列式[15-16]確定船舶不穩定參數圖譜。在確定參數圖譜的過程中,過渡曲線的解φ(t)可用如下傅里葉級數表示: 將式(26)代入式(3),可得 基于式(27),式(3)的系數矩陣行列式表示為 當行列式(28)的值為正時,式(3)對應的解收斂到0,船舶運動處于穩定狀態;當行列式(28)的值為負時,式(3)對應的解呈發散狀態,船舶發生參數共振現象。可通過無限行列式的零解確定上述兩種狀態的過渡曲線,如圖2 所示,其中c 表示阻尼系數。 圖2 參數橫搖穩定圖譜Fig.2 Stability chart of parametric rolling 利用過渡曲線來標定船舶不穩定參數圖譜中的穩定區S 和不穩定區U。顯然,隨著阻尼系數的增大,參數圖譜中的不穩定區間減小。同時,觀察圖2 可知,對于不同的穩定區間,增大阻尼系數c 對過渡曲線極小值的影響尤為顯著。 船舶在海上航行時,遭遇的海況復雜多變。當海浪波高小、周期短時,船舶響應較小;當波高大、周期長時,船舶響應增強,從而引發參數橫搖現象。本文將基于表1 中某船舶的尺寸參數進行運動學特性分析。 表1 某船舶尺寸參數Tab.1 Parameters of the studied ship 根據1.2 節中的解析解,通過改變r 的取值,研究船舶橫搖運動響應。當r=0 時,式(3)為常系數線性齊次微分方程,對應解為正弦信號。基于給定算例,圖3 為r=0 時船舶的橫搖運動狀態圖。圖3(a)給出分別由通解與所求解析解兩種方法得到的船舶橫搖運動時歷圖;圖3(b)表示對應相圖,呈橢圓狀。觀察波形,此時船舶橫搖角表現為正弦波,沒有引起較大橫搖運動,可判斷船舶處于穩定狀態。當r=0.1 時,船舶橫搖運動時歷記錄如圖4(a)所示,在給定時間段0~500 s 內,船舶橫搖角幅度逐漸增大;圖4(b)中相平面軌跡以螺旋線的形式呈現發散狀態。 圖3 r=0 船舶橫搖運動狀態圖Fig.3 Ship roll motion chart of r=0 state 圖4 r=1 橫搖運動狀態圖Fig.4 Ship roll motion chart of r=1 state 根據以上分析,增大小參數r 的值,會改變船舶橫搖角的運動趨勢。 為驗證本文所給解析解的有效性,在船舶不穩定圖譜中選取特殊點驗證其穩定性,二點分別 為A(0.45,0.4),B(0.25,0.2)。據 圖5可知,A 點位于穩定區,B 點則位于不穩定區。 圖5 A、B 兩點的位置分布Fig.5 Distribution of A point and B point 首先對A 點對應參數下船舶的橫搖運動狀態進行預測,取r=0.1。圖6 為船舶橫搖運動狀態圖,圖6(a)表示橫搖角在0~500 s 內的時歷記錄,角幅度控制在0.1 rad 內;圖6(b)呈現出一種概周期運動形式。可判斷該狀態下的船舶處于穩定狀態,分析結果與船舶不穩定參數圖譜中的狀態一致。 保持r=0.1 不變,B 點對應參數下船舶的橫搖運動狀態圖如圖7 所示。顯然,橫搖角隨時間迅速增大,同時相平面以螺旋線的形式呈現發散狀態,此時船舶已發生參數共振現象。 由以上分析可知,解析解所給出的橫搖運動狀態與船舶不穩定參數圖譜的預測結果一致。 根據圖2 可知,增大阻尼可抑制船舶不穩定現象的發生,因此基于圖6 與圖7 中參數,增大阻尼項c 的值,利用解析解分析阻尼對船舶橫搖運動的影響。 圖6 r=0.1,c=0 船舶橫搖運動狀態圖Fig.6 Ship roll motion chart of r=0.1,c=0 state 圖7 r=0.1,c=0 船舶橫搖運動狀態圖Fig.7 Ship roll motion chart of r=0.1,c=0 state 圖8 對應圖6 中的船舶運動狀態參數,設定阻尼系數c=0.01 。對比圖6 船舶橫搖時歷記錄可知,橫搖角隨時間的增加逐漸減小,相圖中的螺旋線在一定范圍內呈現收斂狀態;圖9 對應圖7中的船舶參數,設定阻尼系數c=0.01。顯然,阻尼系數的增大減小了船舶的不穩定程度,但此刻仍處于不穩定中;繼續增大阻尼系數,當c=0.5 時,觀察圖10 發現,船舶橫搖角由0.856 9 rad 逐漸減小,此時可認為船舶恢復到穩定狀態。基于以上對比實驗,進一步說明阻尼對參數共振的發生與否以及參數橫搖共振現象發生后恢復到穩定狀態的程度均有重要影響。 圖8 r=0.1,c=0.01 船舶橫搖運動狀態圖Fig.8 Ship roll motion chart of r=0.1,c=0.01 state 圖10 r=0.1,c=0.5 船舶橫搖狀態圖Fig.10 Ship roll motion chart of r=0.1,c=0.5 state 綜上所述,本文所求解析解可以合理地解釋船舶運動行為,能夠應用于船舶運動狀態的實況分析中。 本文通過分析船舶結構建立橫搖運動微分方程,采用多尺度方法求解其解析解。利用Hill 行列式繪制船舶不穩定參數圖譜,分析不同阻尼下對船舶橫搖運動狀態的影響。基于實際船舶結構參數,改變解析解中小參數r 的取值進而判斷船舶的運動狀態,并預測船舶不穩定參數圖譜中給定點的運動狀態,進而判斷解析解的有效性。同時,為了減小船舶發生參數橫搖的可能性,本文基于解析解考慮了不同阻尼對船舶不穩定狀態的影響程度。主要結論如下: (1)基于文中所得解析解,船舶參數橫搖的發生隨小參數r 的增大而增大,同時相平面會由橢圓狀變為螺旋線,并逐漸呈發散狀態; (2)阻尼越大,船舶不穩定現象發生的可能越小。阻尼對參數橫搖的發生與否以及參數橫搖現象發生后恢復至穩定狀態的程度均有重要影響。 本文得到的解析解可作為分析船舶運動狀態的有效手段,并能對橫搖運動進行預測。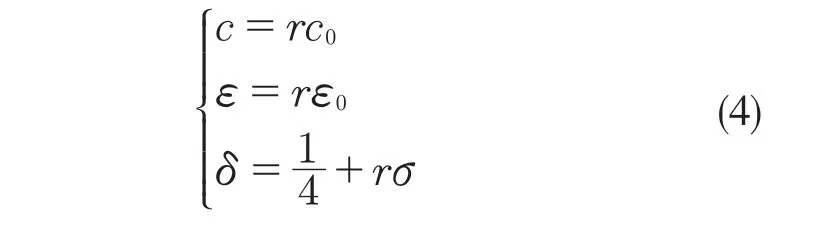
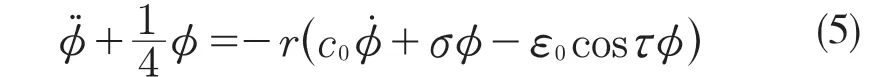
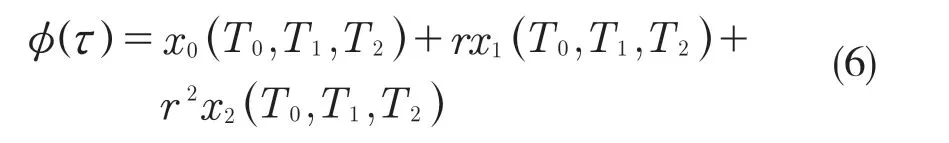
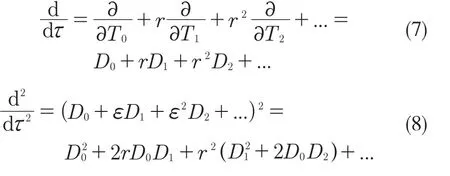
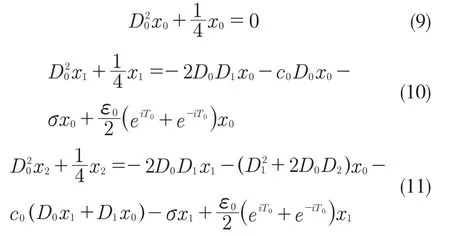
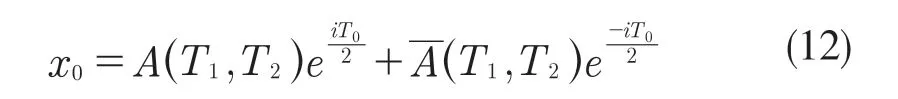
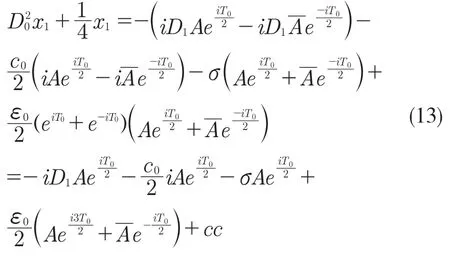
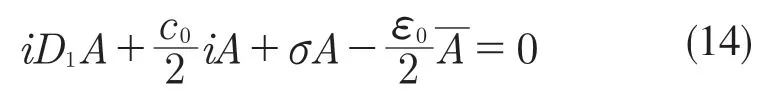
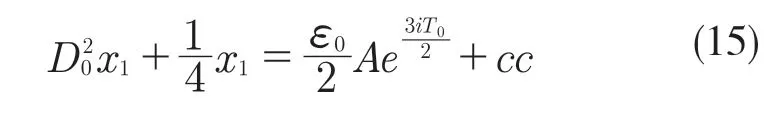
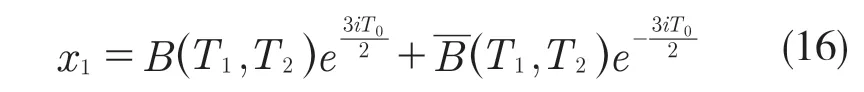
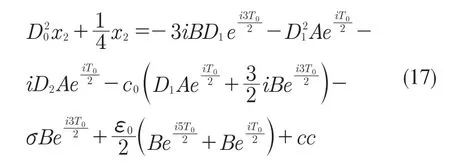
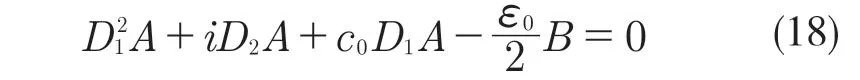
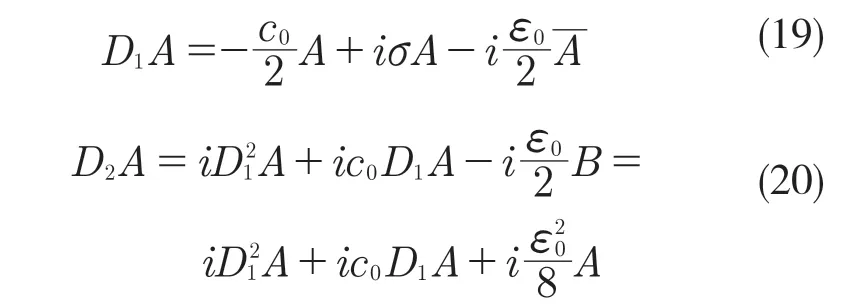
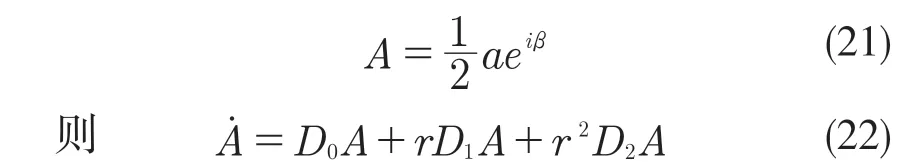
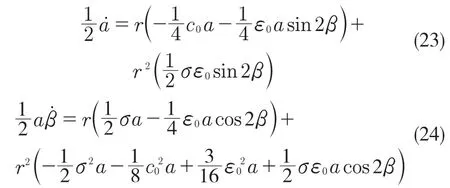

1.3 不穩定區間的確定
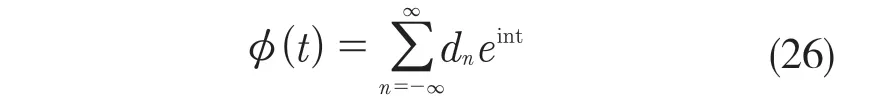
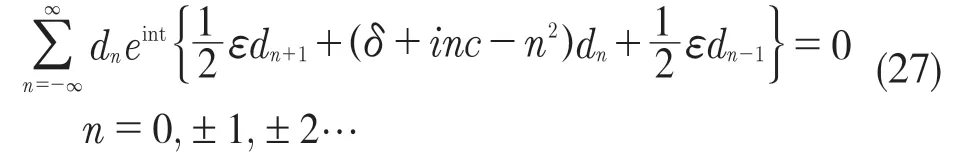
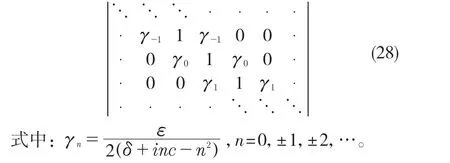

2 船舶橫搖運動響應分析

3 結論

