工程機械液壓缸內泄漏故障檢測分析

黃 克

（德州職業技術學院，山東德州 253034）

0 引言

液壓缸是大型機組設備中不可或缺的重要液壓執行元件，主要用于將液壓能轉變為機械能，并做直線往復或擺動運動[1]。液壓缸結構簡單、工作可靠，用于實現往復運動時無需裝設減速裝置，且沒有傳動間隙，運動平穩，因此在各類機組設備的液壓系統中得到了廣泛應用。但在實際運行期間，液壓缸經常出現泄漏故障。為及時檢測出故障的類型，需探索行之有效的解決方式。

1 液壓缸泄漏原因分析

（1）密封件結構形式與材料因素。如果用于密封的材料質地硬度不足，則在液壓缸處于工作狀態時，密封件十分容易“擠進”密封間隙。在此過程中，液壓缸會出現損傷，逐漸導致液壓油滲漏[2]。

（2）密封槽與密封接觸表面的質量較差。一般情況下，液壓缸密封件安裝在尺寸精度相對較低、表面粗糙程度以及形位公差均較低的密封槽內，密封件會受到磨損，進而泄漏液壓油。

（3）通常而言，對液壓缸密封件的要求為：①尺寸精度必須較高；②形狀位置精度必須準確。若上述兩項精度要求不達標，則密封件在裝配過程中會受到磨損，進而導致內泄漏。

（4）大型機組設備運轉過程中會產生熱量，導致工作環境長時間處于高溫狀態，若不能及時降溫，則密封件的老化速度將會加快。若缺乏有效的檢修維護制度，無法及時發現密封件的老化情況，則密封效果會逐漸降低，最終導致泄漏。

（5）某些液壓缸裝有緩沖閥，在設備運轉期間，閥芯與閥座極易出現磨損情況，同樣會導致液壓缸內泄漏。

2 液壓缸內泄漏故障的檢測方式

2.1 數學建模要素分析

在實際工作中，常用的檢測工程機械液壓缸內泄漏故障的方法主要為經驗診斷法，即觀察液壓系統的工作壓力，若相關參數并未達到標準值，且在調節安全閥的過程中，壓力參數并未出現明顯變化時，便可懷疑液壓缸內有可能出現內泄漏故障。但此種方式的直觀性較低，當技術人員經驗不足時，很可能無法及時發現內泄漏故障，液壓缸及鄰近機組設備均可能受到影響。本研究設計一種基于數學建模方式的液壓缸內泄漏故障的檢測方法，主要原理如下：

（1）所選取的液壓缸系統為負載傳感液壓系統，是非對稱性液壓缸。建立數學模型時，必須具備的參數主要來源于兩個方面：一是液壓缸本身的結構組成；二是液壓缸運行期間產生的參數。具體而言：①液壓缸（泵）出口處的壓力，以p′表示；②液壓泵單位時間的流量，以Q′表示；③液壓缸進油管道的上液阻力，以R1表示；④液壓缸進油管道的流量，以Q11表示；⑤液壓缸回油管道的上液阻力，以R2表示；液壓缸回流管道的流量，以Q21表示；⑥液壓缸內泄漏的液體阻礙壓力，以R 表示；液壓缸內泄漏的流量，以Q 表示；⑦流進、流出液壓缸的流量，分別以Q12、Q22表示；⑧液壓缸進油腔的壓力以及出油腔的壓力，分別以p1和p2表示；⑨在沒有發生內泄漏事故時，對稱液壓缸輸出動力以及出現內泄漏故障時對稱液壓缸的輸出動力分別以F1和F2表示；⑩液壓缸活塞的運動速度，以v 表示。

（2）上述基礎參數僅僅是構建數學模型的基礎參數。除此之外，液壓泵運行期間重要參數之間的關系滿足公式（1）：

式中，Δpλ 是液壓系統運行期間必然產生的“沿程壓力損失”；λ 是沿程阻力系數；l 是管道長度；d 是管道直徑；ρ 是液壓油本身的參數——密度；v 是液壓油的流動速度。q=π/4·d2v 是流量公式，將該公式帶入式（1），得到：

變換后，其中一個變量——液壓油的流動速度v 消失。在剩余的參數中，沿程阻力系數λ、管道長度l、管道直徑d、液壓油密度均是固定值且均為常數。以此為基礎，可定義一個參數R（液壓缸內泄漏的液體阻礙壓力）。具體的關系為：

根據式（3）的構成參數可知，液阻R 的參數是一個固定值（除λ 等參數之外，π 是定值，故R 值也必然固定）。至此完成檢查機械液壓缸內滲漏故障的數學模型，以液阻R 替代繁瑣的參數表示項之后可以發現，液壓系統的沿程壓力損失Δpλ=Rq2。式中唯一的變量即為q，而q 實際上即為液壓油的流量，在條件滿足時可與Q′等參數互相轉換（q 可視為Q′等參數的“替代表示值”）。為進一步增強理論計算過程中的便利性，可將液壓缸內泄漏過程中的液阻R、R1、R2分別與其產生的油液壓力損失（RQ2、R1Q2、R2Q2）相互對應，可使后續計算過程及結果顯示的直觀程度大幅度提升。

2.2 液壓缸的動力特性分析（基于模型闡述）

在液壓缸并沒有出現泄漏事故的情況下，數學模型如圖1所示。基于流體動力學原理，列出圖中相關參數之間的關系：①F2=p1A1-p2A2；②p1=p′-R1Q112；③p2=R2Q212；④v=Q11/A=Q21/A。這4個等式構成模型方程組，經過帶入、消除其中某些參數之后可得出變換后的無泄漏故障時的液壓缸模型動力方程：

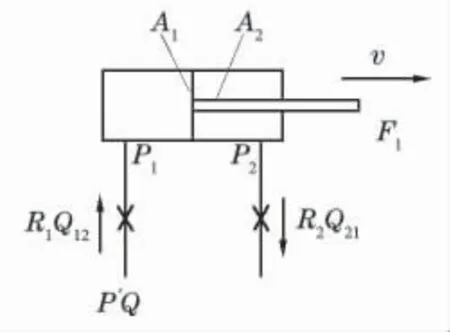
圖1 無泄漏事故時的液壓缸模型

在液壓缸出現泄漏事故之后，數學模型如圖（2）所示。對應的方程組：①F2=p1A1-p2A2；②p1=p′-R1Q112；③p2=R2Q212；④Q11=Q12+Q；⑤Q21=Q22+Q；⑥v=Q11/A=Q21/A。經過變換后得出的各參數之間的關系為：

分析式（4）、式（5）可知，無論液壓缸是否出現內泄漏事故，F 與v 之間的關系仍然為二次函數表達式（參數A 雖然為三次方形式，但并非主要參數，只考慮F 與v 即可）。對式（4）、式（5）進行深入分析后發現，機械液壓缸中是否存在輸出動力并不取決于p1是否＞p2。在此基礎上，根據數學模型中的某些參數之間的相互關系，即可判斷液壓缸的泄漏情況。具體而言：第一，若p1＞p2，則Q＞0，此時，液壓缸必定存在泄漏情況，泄漏方向與圖2所示方向一致；第二，若p1=p2，則Q=0，表明液壓缸處于正常運轉狀態，不存在內部泄漏情況；第三，若p1＜p2，則Q＜0，此時液壓缸的流量方向與內泄漏方向（即圖2 顯示方向）相反。

圖2 出現泄漏事故時的液壓缸模型

將式（4）、式（5）整理后得出：

由上文所述可知，F 與v 之間的關系呈二次函數剖物線形態，且在液壓缸內沒有出現泄漏情況時，F2-V 與兩條剖物線必定會在直角坐標系中的一個點位相交。將有關項合并之后，可得出：

2.3 液壓缸內泄漏事故發生時的常見特性分析

再次對式（4）、式（5）進行分析后可以發現，當Q＜0 時，的絕對值必定會小于dF2/dv 的絕對值，且的曲線與的曲線在C 點相交。根據模型所示結果，當液壓缸承受較大負載時（通常運行速度會有所降低），如果出現內泄漏事故，則液壓缸的運行速度必定也隨之降低（即同等負載下，無泄漏狀態下的液壓缸運行速度超過有泄漏事故時的運行速度）。

2.4 數學建模檢測法的液壓缸內泄漏故障檢測實踐分析

（1）首先正常啟動液壓缸，并將液壓油加入油腔內。在此狀態下，進油腔的壓力逐漸升高，并能夠與執行元件的負載保持平衡。受“油液具備可壓縮性”這一特點的影響，進油腔產生的壓力不會立刻達到與負載相同的水平，而是呈現出“漸變”的特性。實際結果顯示，該過程的壓力上升具有跳躍性。

（2）繼續控制油液進入油腔，且需保證活塞可以平穩伸出，一直持續到活塞伸出到最大位置處（也可在執行元件的負載進入“無限大”時停止）。

按照上述流程，模擬液壓缸未出現內泄漏、出現輕微內泄漏、嚴重內泄漏的情況，最終結果顯示，基于數學模型的壓力曲線變化情況存在差異。

3 結語

綜上所述，本文基于數學建模法，將液壓缸運行期間的各項參數設置為運行構成主參數，經過消除部分變量的轉換之后，得出F 與v 之間存在二次函數關系。以此為基礎，得出“同等負載下，無泄漏狀態下的液壓缸運行速度超過有泄漏事故時的運行速度”[3]的結論，試驗結果表明該結論是正確的，表明基于數學建模的檢驗方法具備可行性。