一類比率型Holling-Leslie 趨化模型的分支結構

張 望, 李艷玲, 周 浩

(陜西師范大學數學與信息科學學院，西安 710119)

1 引言

本文考慮如下帶有食餌趨化項的Holling-Leslie 捕食-食餌模型

與模型(1)相關的常微分模型最早由Leslie[1,2]提出，Leslie 捕食模型主要強調了捕食者的環境容納量和食餌的數量成正比，后來Li 和Xiao[3]、Wang 等[4]在Leslie 模型的基礎上研究了比率依賴的Leslie 捕食-食餌模型，討論了平衡態和分歧解的存在，并進行了數值模擬相應的結果.對于模型(1)的常微分模型，即Holling-Tanner 模型[5]，在文獻[6,7]中主要討論了Holling-II 型功能反應的Leslie 模型，主要研究了正平衡點的全局漸近穩定條件，系統的局部穩定性，全局穩定性，以及穩定的極限環和半穩定的極限環等問題.文獻[8]討論了Holling-III 型的Leslie 模型，得到了局部分支解的存在性條件，并給出了一維情況下整體分支解的性態.

在生態環境中，物種間的相互作用和物種的進化非常重要.通常通過交叉擴散模型來描述，模型(1)中的χ?(u?v)項就是一種趨化作用的交叉擴散項，在生態學背景下，由于一些化學信號的作用，物種會向特定的方向運動，我們依據生物對化學信號的靠近和遠離，將趨化作用分為趨化吸引和趨化排斥.最早的趨化模型由Keller 和Segel[9]提出，在文獻[10-12]中提出了相關的吸引-排斥趨化模型，用來描述物種的群體效應和細胞的聚集現象.因此趨化在生物控制和生態平衡中起著重要的作用.

本文主要對模型(1)的線性穩定性進行分析，得到唯一正常數平衡解(u?,v?)，應用Crandall-Rabinowitz 分支理論，以趨化敏感性系數χ為分支參數，討論了二維空間區域上非常數正解的結構和分支方向，從而刻畫了時空斑圖的結構.

2 穩定性分析

則當a ＞a0時，(u?,v?)是漸近穩定的.

證明 系統(2) 在(u?,v?)處的Jacobi 矩陣為

其中f2＜0, g1＞0, g2＜0，考慮該算子的特征方程為μ2-T(a)μ+D(a)=0.

經計算可得

假設(h(x),k(x))是L對應于特征值μ的特征函數，則有

注1 注意到此時算子L是退化的，定理1 中g1＞0.得到下面的推論.

推論1 若對所有的i ≥1, Pi(λi,0)＜0, Qi(λi,0)＞0 均成立，則當χ ＞0 時，(u?,v?)作為系統(3)的唯一正常數平衡點是局部漸近穩定的.這表明當捕食者對食餌是趨化吸引時，并不影響無趨化時正常數平衡點的穩定性.

推論2 若Pi(λi,0)＜0 總成立，記集合k ={i|i ≥1,Qi(λi,0)＜0}表示存在一些i ≥1，使得Qi(λi,0)＜0 的集合.此時χi ＞0，則對所有的χ ＞maxi∈kχi，(u?,v?)在系統(3)中是局部漸近穩定的.這說明在沒有趨化現象時，由于系統擴散項導致的不穩定性，會因為趨化吸引的出現而將這種不穩定變得穩定，從而抑制斑圖的生成.

推論3 若Pi(λi,0)＜0, Qi(λi,0)＞0 總成立，此時χi ＜0，則對所有的χ ＜max1≤i＜+∞χi，系統(3)的唯一正常數平衡點(u?,v?)是不穩定的.這意味著當出現趨化排斥時，會將系統(2)和只有擴散項的系統(3)(χ= 0)中常數平衡點的穩定性變得不穩定，從而造成斑圖出現.

3 局部分支

在這一節主要來驗證推論3，由前面分析可知，當f1＜0 時，Pi(λi,0)＜0, Qi(λi,0)＞0 總成立.下面將在f1＜0 的條件下，以趨化敏感性系數χ ＜0 為分支參數，在二維空間區域上應用分支理論，討論非常數正解的結構，進而說明趨化排斥確實能夠造成時空斑圖的生成.

方便起見，給出下面一些記號，定義二維空間區域

Hilbert 空間

根據隱函數定理可知，當χ=χ(i,j)時，算子L(u,v)(χ;u?,v?)是退化的，(χ(i,j);u?,v?)才可能是分支點.注意到局部分支定理要求線性化算子的核空間維數是一維的，由于

而(i,j)和χ(i,j)之間不是一一對應的關系.例χ(1,1)=χ(2,0), χ(1,3)=χ(4,2)，所以僅考慮χ(1,0)和χ(0,1)的情況.

定理2 假設f1＜0 成立，如果dimKerL(u,v)(χ(i,j);u?,v?) = 1，則存在一個正常數δ，使得系統(3)在點(χ(i,j);u?,v?)鄰域中的非常數正解可以表示為

至此，由局部分歧定理知，系統(3)存在唯一一條由(χ(i,j);u?,v?)分支出的非平凡解曲線(χ(i,j);us,vs)，其中

4 分支方向

本小節的主要內容是給出～χ(0)的具體表達式，因為它決定定理2 中所得到的局部分支解的分支方向，若～χ(0)＞0，則稱分支式(6)是超臨界的；若～χ(0)＜0，則稱分支式(6)是次臨界的；所得結果表明～χ(0)的具體表達式由四個L2內積組成

定理3 (A,B,C,D)滿足如下代數方程

證明 由分部積分公式可以計算得到

將(χ(s);us,vs)代入系統(3)第二個方程，并關于s求導兩次后令s=0，得到

整理得

類似計算可以得到

結合(10)-(13)，定理3 得證.

定理4 分支式(6)中的～χ(s)滿足下面表達式

證明 對(8)式關于s求導，并令s=0，計算得

定理4 得證.

5 例子和數值模擬

圖1 a=0.3 時，系統(2)的相圖

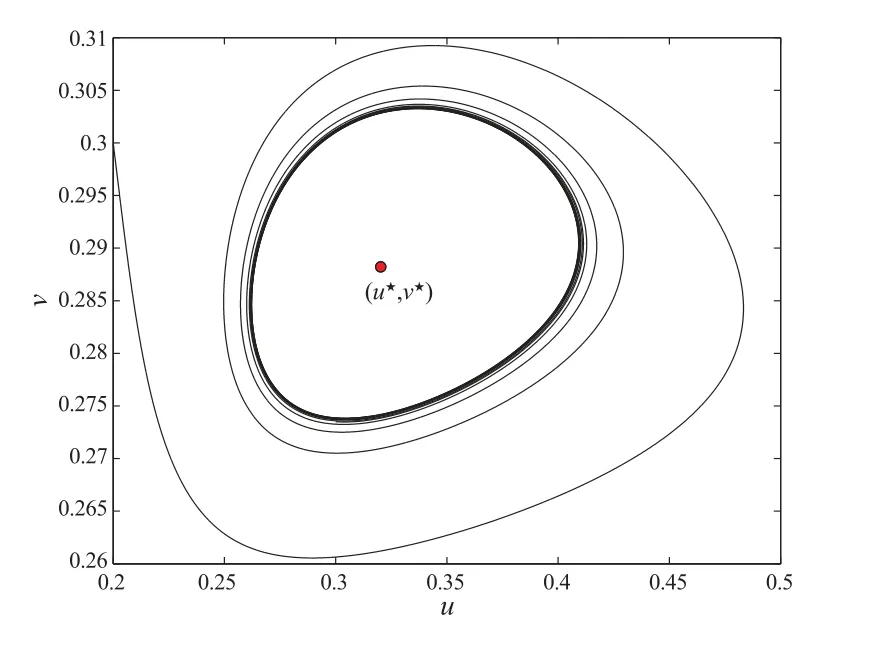
圖2 a=0.02 時，系統(2)的相圖

圖3 系統(1)不含趨化項時，(u(x,t),v(x,t))的數值解

圖4 系統(1)出現趨化排斥時，u(x,t)的數值解

圖5 系統(1)出現趨化排斥時，v(x,t)的數值解

圖6 系統(1)出現趨化吸引時，u(x,t)的數值解

圖7 系統(1)出現趨化吸引時，v(x,t)的數值解