3-PRC并聯(lián)機構(gòu)的運動學(xué)性能與仿真*

沙鑫美， 呂小祥

(1. 三江學(xué)院 機械與電氣工程學(xué)院， 南京 210012； 2. 江蘇南京熱電工程設(shè)計院 設(shè)計部， 南京 210000)

并聯(lián)機構(gòu)是不少于兩條的獨立支鏈連接靜平臺與動平臺的閉環(huán)系統(tǒng)，具有高穩(wěn)定性、高精度、高強度和低誤差等特點，廣泛應(yīng)用于精密加工與材料科學(xué)等領(lǐng)域.并聯(lián)機構(gòu)又可分為六自由度、三自由度和二自由度等多種類型.

目前，三自由度的并聯(lián)機構(gòu)廣泛應(yīng)用于實際工作場合，且自由度較少，主要由球面、平移和混合等3類并聯(lián)機構(gòu)組成.由于三自由度并聯(lián)機構(gòu)具有結(jié)構(gòu)簡易、承載性較強和誤差較小等優(yōu)點，該并聯(lián)機構(gòu)也成為學(xué)者研究的重點對象.其中，Yue等[1]參考Delta并聯(lián)設(shè)備的結(jié)構(gòu)，提出了具有三維移動能力的并聯(lián)微操作機構(gòu)；高繼良等[2]設(shè)計與分析了具有對稱結(jié)構(gòu)的3-TRT并聯(lián)機構(gòu)；Zeng等[3]提出具有三平移輸出的Tri-pyramid型并聯(lián)機器人；吳騰等[4]研究了3-UPU并聯(lián)機構(gòu)，同時設(shè)計分析了3-UPU的變胞機構(gòu).上述研究均是對稱型的三平移并聯(lián)機構(gòu)，分別具有結(jié)構(gòu)簡易、工作空間大、造價低等特點.

為增強并聯(lián)機構(gòu)的運動學(xué)性能，本文在以往研究[5-8]的基礎(chǔ)上，提出3-PRC三平移的并聯(lián)機構(gòu).其中，“3”表示其末端輸出自由度，“P”表示prismatic joint，即支鏈的聯(lián)接副為移動副；“R”表示rotation joint，即聯(lián)接副為轉(zhuǎn)動副；“C”表示cylinder joint，即聯(lián)接副為圓柱副.與以往研究相比，本文3-PRC并聯(lián)結(jié)構(gòu)主要具備3個優(yōu)點：1)該機構(gòu)的動平臺輸出無轉(zhuǎn)動，且具有3個平移自由度；2)所有支鏈對稱，且各向同性；3)該機構(gòu)的運動副均是低副，所以其加工精度和承載能力較高.

1 3-PRC并聯(lián)機構(gòu)的構(gòu)型描述

本文設(shè)計的3-PRC并聯(lián)機構(gòu)的構(gòu)型如圖1所示.在該構(gòu)型中，利用轉(zhuǎn)動副R、圓柱副C和移動副P組成3條支鏈，并聯(lián)機構(gòu)的靜平臺與動平臺相連.其中，圓柱副由一個轉(zhuǎn)動副和同軸移動副組成，而轉(zhuǎn)動副與圓柱副的回轉(zhuǎn)軸線平行.

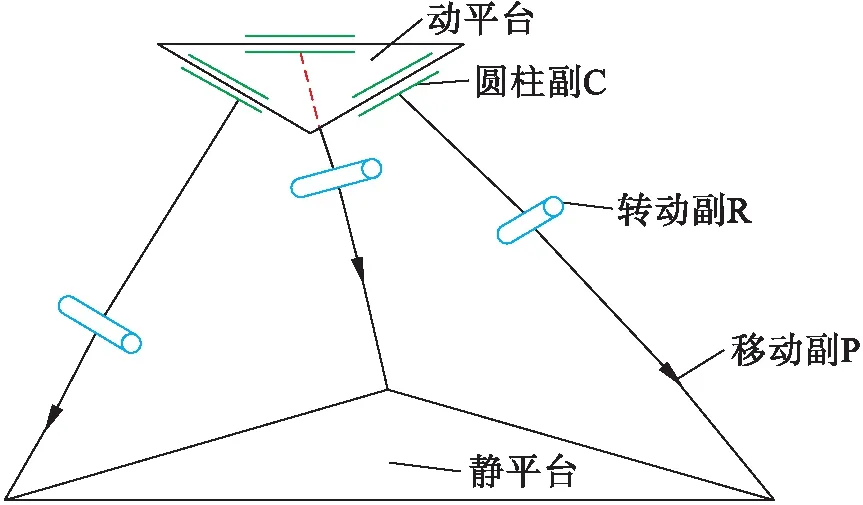
圖1 3-PRC并聯(lián)機構(gòu)構(gòu)型圖Fig.1 Configuration of 3-PRC parallel mechanism

2 運動學(xué)研究

運動學(xué)研究是對并聯(lián)機構(gòu)性能進行分析的基礎(chǔ)，其研究對象是動平臺末端輸出、機構(gòu)構(gòu)成和驅(qū)動之間的運動關(guān)系，即分析末端輸出與機構(gòu)組成的位移、速度和加速度.為分析并聯(lián)機構(gòu)的運動學(xué)位置，本文首先計算3-PRC并聯(lián)機構(gòu)的自由度數(shù)量，再建立相應(yīng)的坐標系；然后求出并聯(lián)機構(gòu)的位置正解和反解，從而利用機構(gòu)的運動影響系數(shù)，分析并聯(lián)機構(gòu)的速度、加速度和奇異性.

2.1 自由度計算

在分析動平臺輸出自由度過程中，本文使用螺旋理論進行具體的研究.由圖1可知，本文提出的3-PRC并聯(lián)機構(gòu)的所有PRC支鏈均由圓柱副C、轉(zhuǎn)動副R和移動副P組成，而移動副P與轉(zhuǎn)動副R均可使用螺旋系表示.其中，移動副P的節(jié)距為無窮大，而轉(zhuǎn)動副R為0，即PRC支鏈的螺旋系Si(1≤i≤4)表達式為

(1)

式中，e2、f2、e4和f4為PRC支鏈上運動副的空間位置數(shù)據(jù).根據(jù)螺旋系的相關(guān)理論可知，支鏈的運動螺旋與約束螺旋之間具有互易關(guān)系；另外，兩者的互易積是0，則可得到其支鏈的約束螺旋S′i(1≤i≤2)，其表達式為

(2)

由式(2)可知，該支鏈具有兩個約束Y軸和Z軸的旋轉(zhuǎn)自由度.同理，其他支鏈的約束螺旋也具有兩個旋轉(zhuǎn)自由度[9-10].由于3個轉(zhuǎn)動自由度均被固定，但動平臺的移動自由度未被約束，則動平臺末端不能自由轉(zhuǎn)動，即該并聯(lián)機構(gòu)的輸出是三維的平動.

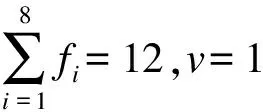
根據(jù)計算結(jié)果可知，3-PRC并聯(lián)機構(gòu)的末端自由度為3.

2.2 坐標系建立

根據(jù)并聯(lián)機構(gòu)的結(jié)構(gòu)，可設(shè)其靜平臺與動平臺分別是邊長為a、中心為O和邊長為b、中心為P的正三角形.利用這兩個中心，分別建立坐標系O-XYZ和P-xyz，如圖2所示.圖2中，動平臺中心P在O-XYZ中的坐標為(xP，yP，zP).

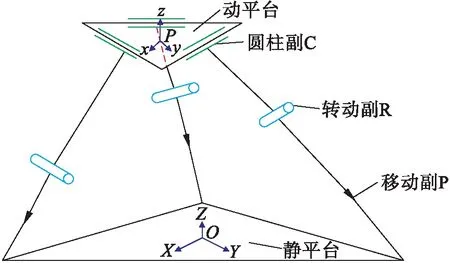
圖2 3-PRC并聯(lián)機構(gòu)坐標系Fig.2 Coordinate system of 3-PRC parallel mechanism

2.3 位置正反解

在建立如圖2所示的坐標系后，由于支鏈與靜平臺之間用驅(qū)動桿連接，可設(shè)支鏈與靜平臺平面的夾角為α，其長度為d，滑動距離為li，圓柱副的連接桿長度為hi，與靜平臺平面的夾角為θi，滑動距離為si.

驅(qū)動桿的滑動距離是并聯(lián)機構(gòu)的位置反解.為求解該數(shù)值，已知動平臺中心P的坐標為(xP，yP，zP)，本文列舉第一個支鏈的方程組為

(3)

根據(jù)并聯(lián)機構(gòu)的結(jié)構(gòu)，相對于z軸，3個支鏈以120°分布.將第一個支鏈旋轉(zhuǎn)120°和240°，可得到如下兩個方程組，即

(4)

(5)

聯(lián)立式(3)～(5)得

(6)

將式(6)整理，求解可得

(7)

式中：W1=W2=W3=1；且

此時，利用動平臺中心P的坐標(xP，yP，zP)，即可求解得到3-PRC并聯(lián)機構(gòu)的位置反解.而對于該并聯(lián)機構(gòu)的位置正解，若已知驅(qū)動桿的滑動距離li(i=1，2，3)，利用式(6)可以求得動平臺中心P的坐標(xP，yP，zP)，即可求解得到3-PRC并聯(lián)機構(gòu)的正反解.

2.4 速度和加速度

為獲取3-PRC并聯(lián)機構(gòu)的運動狀態(tài)，本文使用運動影響系數(shù)法分析其速度和加速度.式(6)是3-PRC并聯(lián)機構(gòu)的運動方程式，利用廣義坐標可表示為

U=f(I，Φ0)=0

(8)

式中：Φ0為動平臺中心P的坐標(xP，yP，zP)；I為驅(qū)動桿的滑動距離(l1，l2，l3).分別對時間t進行求導(dǎo)，可得

(9)

展開式(9)可得

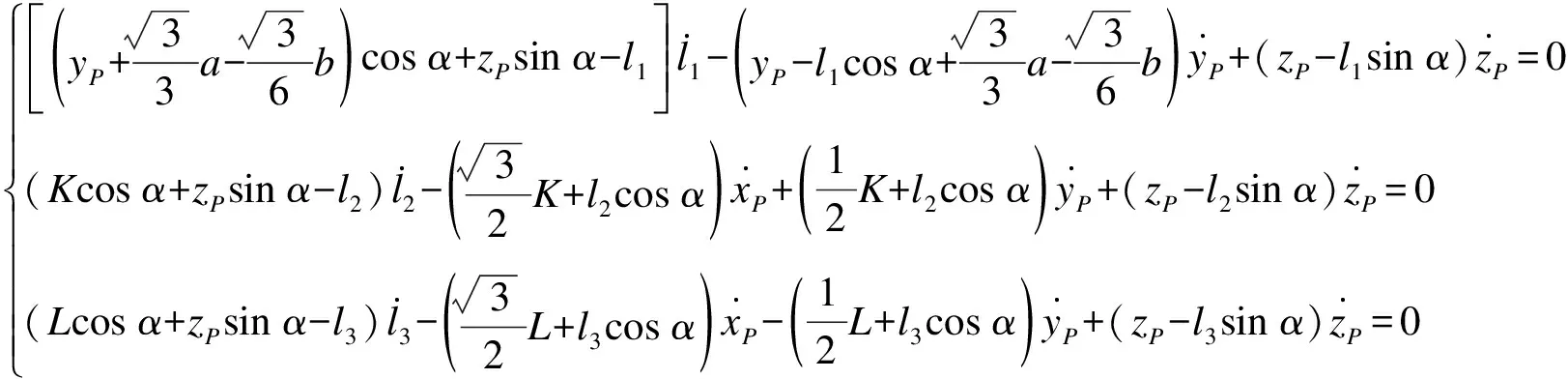
(10)

式中，驅(qū)動中間變量K和L的公式分別為

(11)

展開可得

(12)

式中，雅克正矩陣和逆矩陣的分量mi和eij的表達式為

(13)

利用式(13)可求解具有3個維度的二階影響系數(shù)矩陣，即

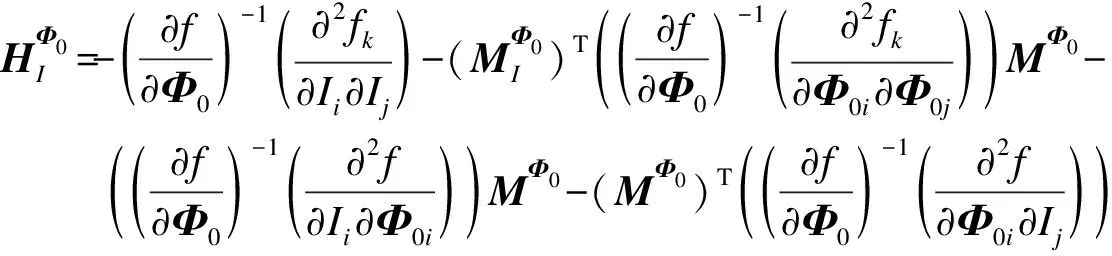
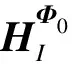
(14)

3 仿真分析

利用ADAMS軟件對3-PRC并聯(lián)機構(gòu)進行三維建模.通過仿真驗證分析結(jié)果，為并聯(lián)機構(gòu)的具體控制提供相應(yīng)的理論依據(jù).

3.1 逆運動學(xué)仿真

使用動平臺中心點固定的運動軌跡，通過ADAMS軟件即可計算出并聯(lián)機構(gòu)驅(qū)動模塊的位移、速度和加速度.令t表示時間，設(shè)定End time為10 s，Steps為1 000.則本文動平臺中心點P的曲線軌跡方程為

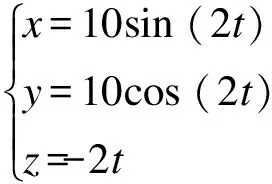
(15)

當(dāng)該動平臺中心點按照以上方程進行運動時，本文測試驅(qū)動模塊的位移、速度和加速度，得到的曲線如圖3～5所示.

3.2 正運動學(xué)仿真

當(dāng)3-PRC并聯(lián)機構(gòu)的驅(qū)動桿輸入確定時，本文仍可以對該機構(gòu)的動平臺中心點輸出進行仿真.在仿真中，設(shè)定End time為10 s，Steps為1 000.同時向ADAMS軟件中導(dǎo)入3個Splines函數(shù)曲線，作為驅(qū)動桿的輸入，即

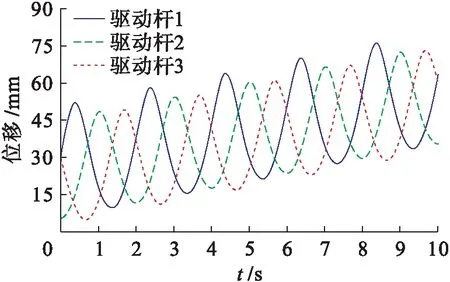
圖3 驅(qū)動模塊的位移曲線Fig.3 Displacement curves of driving module

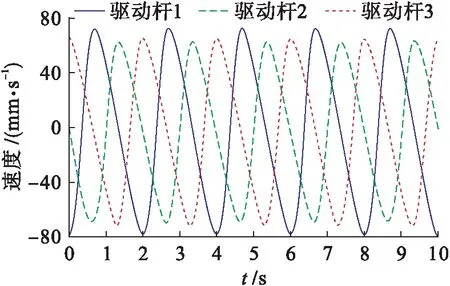
圖4 驅(qū)動模塊的速度曲線Fig.4 Speed curves of driving module

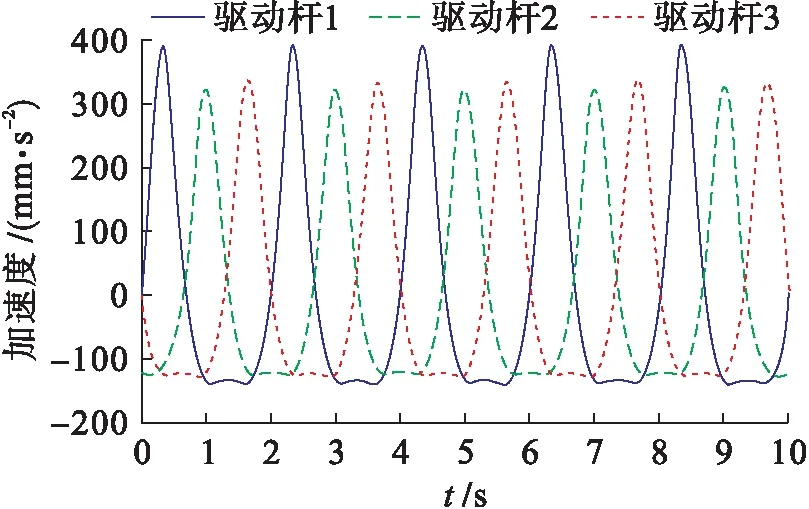
圖5 驅(qū)動模塊的加速度曲線Fig.5 Acceleration curves of driving module

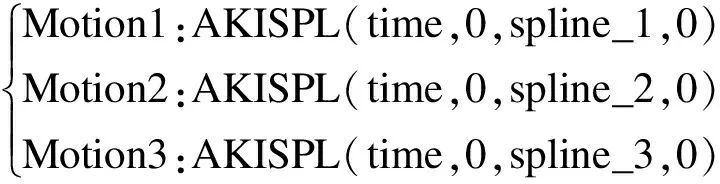
利用以上參數(shù)運行ADAMS軟件，可以統(tǒng)計得到動平臺中心點的位移、速度和加速度曲線，分別如圖6～8所示.

由圖3～8可知，在3-PRC并聯(lián)機構(gòu)的正逆運動學(xué)仿真中，其驅(qū)動模塊與動平臺中心點的軌跡位移均一致，3個驅(qū)動桿之間沒有互相干涉的情況，同時其速度和加速度均無突變.仿真結(jié)果表明，3-PRC并聯(lián)機構(gòu)的設(shè)計合理，且其正反解與模型的理論分析結(jié)果均正確無誤.

3.3 有限元分析

為了進一步分析3-PRC并聯(lián)機構(gòu)的性能，本文對該機構(gòu)進行了有限元分析，選取了一種特殊位姿，即將并聯(lián)機構(gòu)置于工作空間的邊界附近.在這個狀態(tài)下，動平臺和其他部件的變形均很嚴重，整個機構(gòu)處于嚴重的受力不均勻狀態(tài)，從而檢測并聯(lián)機構(gòu)的危險部位.

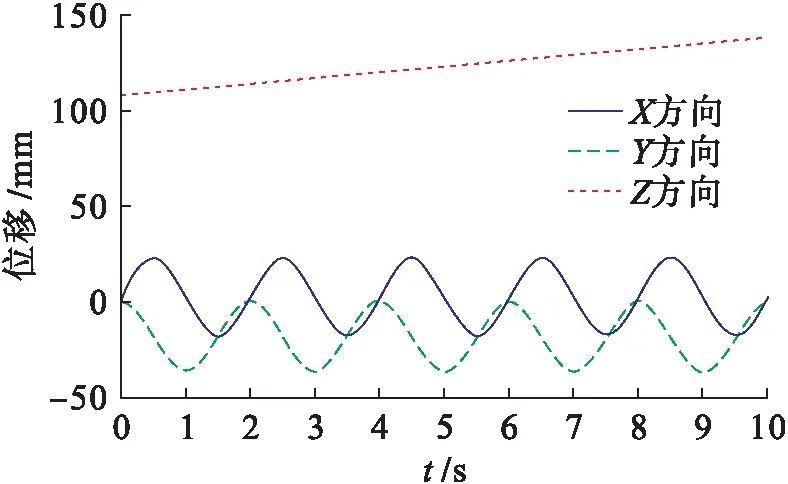
圖6 動平臺中心點的位移曲線Fig.6 Displacement curves of center point of motion platform

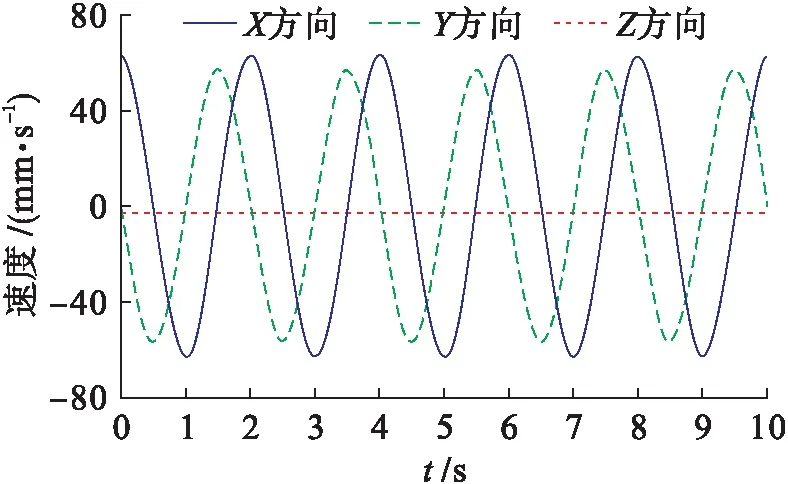
圖7 動平臺中心點的速度曲線Fig.7 Speed curves of center point of motion platform

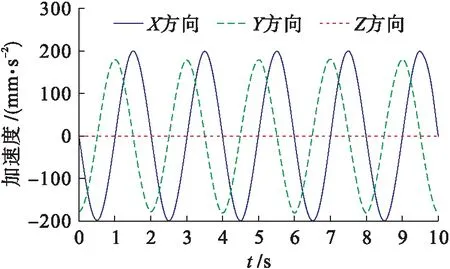
圖8 動平臺中心點的加速度曲線Fig.8 Acceleration curves of center point of motion platform

有限元分析主要有預(yù)處理、分析計算和處理三個步驟.在預(yù)處理過程中，本文分析了并聯(lián)機構(gòu)的材料屬性、裝配方式和關(guān)系，使用ANSYS軟件添加移動副、轉(zhuǎn)動副和圓柱副等約束和接觸，得到的模型如圖9所示.當(dāng)并聯(lián)機構(gòu)的動平臺承受垂直向下且大小為100 N的力時，并聯(lián)機構(gòu)發(fā)生了較大的變形，結(jié)構(gòu)圖如圖10所示.

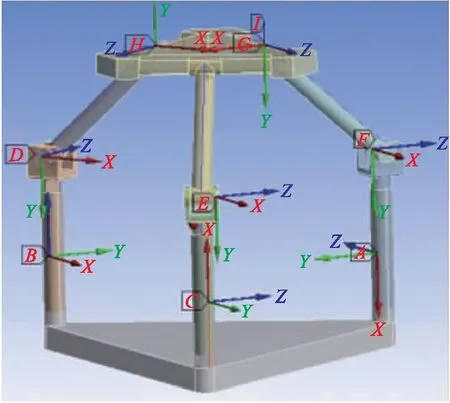
圖9 3-PRC并聯(lián)機構(gòu)的軟件模型Fig.9 Software model for 3-PRC parallel mechanism

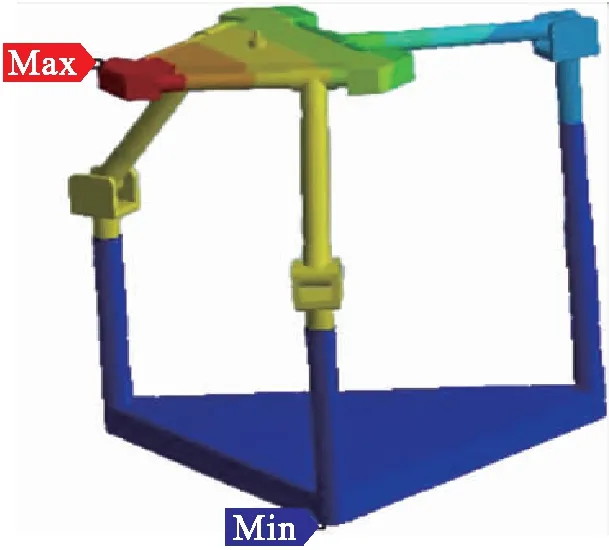
圖10 3-PRC并聯(lián)機構(gòu)變形結(jié)構(gòu)圖Fig.10 Deformation structure diagram of 3-PRC parallel mechanism

經(jīng)過ANSYS軟件分析可知，在受力條件下，并聯(lián)機構(gòu)的最大變形量為7.843 2×10-2mm，最大應(yīng)力值為40.658 MPa，最小安全系數(shù)為6.121.一般來說，抗不穩(wěn)定系數(shù)的取值范圍為[3，5]，最小安全系數(shù)距離這個范圍越遠越好.因為最小安全系數(shù)為6.121，所以本文的并聯(lián)機構(gòu)尺寸是合理的，結(jié)構(gòu)基本達到安全標準.

4 結(jié) 論

本文對3-PRC并聯(lián)機構(gòu)進行了設(shè)計與建模，通過理論推導(dǎo)與軟件仿真的方式詳細分析了其運動學(xué)性能，仿真結(jié)果驗證了理論推導(dǎo)的正確性和安全性.通過ANSYS軟件仿真可知，本文所設(shè)計的并聯(lián)機構(gòu)的安全性有待提高，即最小安全系數(shù)與抗不穩(wěn)定系數(shù)的取值范圍距離仍然較小，存在一定的優(yōu)化空間，未來將繼續(xù)優(yōu)化并聯(lián)機構(gòu)的設(shè)計，提高其最小安全系數(shù)指標.