基于超材料天線的超分辨關聯成像的改進

阮 鋒, 盧夏雷, 郭 亮,*, 李亞超

(1. 西安電子科技大學物理與光電工程學院, 陜西 西安 710071;2. 西安電子科技大學電子工程學院, 陜西 西安 710071)

0 引 言

微波關聯成像自2010年首次提出以來,經過近10年的發展已經逐漸完善。其在隨機輻射場的產生和成像算法方面都有許多發展,已經有多種不同的技術與方法。

在隨機輻射場的產生方面人們已經研究出許多種方法,如傳統的對各輻射單元的激勵信號進行隨機調制[1-2]、在隨機調制的基礎上進一步對輻射單元空間布局優化等[3-4]。近幾年出現了一種利用超材料對不同頻率的信號可以產生不同調制結果的特性超材料天線[5-7]。2017年西安交通大學的張安學等人提出了一種超材料天線[8]。該天線與現有的微波關聯成像發射系統相比,不需要大規模的發射陣列,只有一個發射天線。這種超材料天線和相控陣天線相比，不僅極大的簡化了天線的系統，而且大幅降低了成本。

在成像算法方面,最初的一階關聯處理算法[9]雖然計算速度快,但是副瓣較高,成像質量不好。Meng提出的基于Krylov子空間的關聯處理算法[10],同時具有較快的計算速度和較好的成像質量。何學智研究了Tikhonov正則化方法[11],提高了成像的抗噪性能，進一步提高了成像質量。由于雷達目標通常具有稀疏或者塊稀疏特性,基于稀疏恢復的關聯成像算法也被研究出來。何學智將稀疏貝葉斯[12-14]等經典稀疏算法引入關聯處理。最近一種利用壓縮感知原理的算法進一步提高了成像的分辨率,其分辨率可以超過瑞利衍射極限,是一種超分辨的關聯成像算法。

前面介紹了隨機輻射場的產生和成像算法兩個方面的各種方法,可以看出隨機輻射場的產生這方面,超材料天線有著系統簡單、成本低、輕便等優勢,但是對于信號的變頻要求是一個不足之處。而成像算法方面,最近的基于壓縮感知的超分辨關聯成像算法的成像質量高,分辨率高,計算速度較快,但是目前沒有能處理變頻信號的方法。故本文提出一種基于壓縮感知的超分辨關聯成像的改進,使這種算法可以處理變頻信號以配合超材料天線使用。

1 關于超材料天線

超材料是一類由人工設計微結構單元周期性排列組成的人造材料,在波動載荷激勵下微結構單元可以產生力學、電磁等方面的諧振響應,因此通過有意調節局部諧振和加載波動載荷的關系,可以使其在宏觀等效意義上具備傳統材料不具備或很難具備的新異電磁、力學材料屬性。超材料的出現極大改變了人類對材料屬性的客觀認識,拓寬了工程材料的設計范圍,提供了人為通過材料設計實現對波的控制可行的手段和技術,使得這類材料在電磁波成像、隱身以及工程隔震和低頻降噪等科學及工程領域有著廣闊的應用前景。

超材料特性研究前期主要集中在光學頻段[15-17],隨后微波超材料的研究也逐漸發展起來。微波超材料的研究首先是采用各種不同的超材料單元驗證各種反常參數(主要是相位)下各種特殊現象的驗證,然后利用已有的理論嘗試對其特性進行解釋[18-21]。針對不同的用途,超材料單元的結構各有特色,而在超材料孔徑成像的應用,主要關注超材料單元的可調控特性與寬帶特性[20-24],典型具有寬帶特性的超材料單元結構及其寬帶特性如圖1所示。

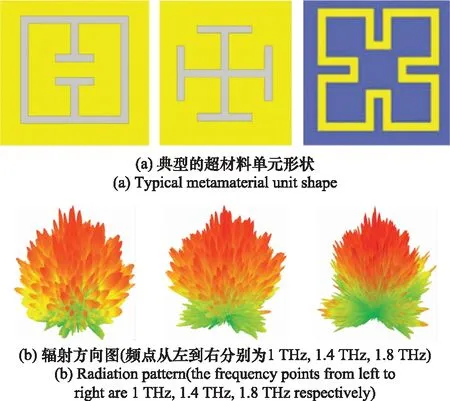
圖1 典型的超材料單元及其輻射方向圖Fig.1 Typical metamaterial unit and its radiation pattern

不管是在頻率域、時域還是隨機輻射碼域進行隨機輻射方向圖掃描,輻射方向圖的隨機特性評價標準是統一的，即在統計域中,任意兩個統計點上的超材料天線輻射方向圖之間的相關性達到最小(理想情況下)[25-26],以此為目標對超材料單元進行設計是超材料天線設計的基礎。當超材料單元樣本足夠多的情況下,可以通過優化方法對所需的方向圖進行設計[27]。而當超材料天線隨機輻射方向圖的隨機波前被實時改變來對目標進行探測時,其探測方式就具有了非相干探測系統的特點[28]。

超材料天線由于超材料的特性,其產生的隨機輻射場的方向圖只與超材料單元的結構和信號的載頻有關。而超材料天線的超材料單元的結構在設計好之后是固定不變的,故在指定的載頻下可以得到的隨機輻射場的方向圖是固定不變的。這一點相比于相控陣隨機調相產生的隨機輻射場[29]具有更加穩定的特點。再加上超材料天線本身不需要相控陣那些大量的發射陣元,使得生產成本相比相控陣也大幅降低。故隨著超材料技術的飛快發展,未來在某些領域逐步取代相控陣也是必然的趨勢。

2 載頻變動產生的誤差分析

首先,關聯成像利用的就是一幅幅的隨機輻射場的方向圖與其對應接收到的回波相關聯,從而解出場景的散射系數,得到成像結果。而本文采用的產生隨機輻射場的方式是超材料天線在載頻不同的信號刺激下會產生隨機的電磁輻射場。所以,要使用超材料天線,就勢必要考慮發射信號的載頻變動而引起的誤差。

通常雷達采用的是線性調頻信號,通過分析仿真線性調頻信號產生的回波與載頻有變動的線性調頻信號產生的回波。

假設雷達發射線性調頻信號為

(1)

發射信號經過場景目標點散射后接收到的回波經過去載頻處理后的基頻回波為

(2)

如果雷達發射載頻步進的線性調頻信號為

(3)

式中：Δf是每次發射脈沖時載頻的變化量,由于載頻在每次發射時逐步遞增故公式中載頻為fc+qΔf。

同樣,其基頻回波為

(4)

3 關聯成像算法

在相控陣中,產生和發射的是線性調頻信號不需要載頻的跳變,也就是說,回波經過下變頻之后的基頻相位只和目標距離有關。但是由于相控陣成本較高,系統設計也較為復雜,采用單一發射天線的超材料天線,與相控陣相比不需要大規模發射天線組陣,相應的成本就降低了很多。但是這種天線存在一個問題,那就是需要給予不同頻率的信號才能得到隨機的輻射場。與相控陣相比,這就需要考慮頻率變動所產生的影響(在仿真中可以明顯看到頻率變動過大，如果不采取補償措施會導致無法成像)。為了解決這個頻率變動造成的影響,改進了基于壓縮感知的超分辨關聯成像的算法,使其可以處理步進頻信號。本節首先對基于壓縮感知的超分辨關聯成像算法[30-31]進行介紹,然后介紹改進后的算法。

3.1 基于壓縮感知的超分辨關聯成像算法

壓縮感知理論表明,當滿足非相關測量和原始信號稀疏性條件下,用遠低于Nyquist采樣定理要求的采樣次數對信號進行采樣時,也可以很好地恢復出原始信號。在關聯成像中,成像的對象即目標場景滿足壓縮感知的稀疏性,而發射和接收的天線都是隨機輻射場,這也滿足了壓縮感知的非相關測量這一條件。

雷達所接收到的回波是經過發射天線調制的發射場與目標散射場相互作用再由接收天線調制接收到的接收場。把場景按等角度間隔離散化形成一個矩形成像網格。假設方位等角度間隔為Δθ,俯仰等角度間隔為Δβ,其把場景分成了方位向Nθ個單元,俯仰向Nβ個單元的矩形網格,總的單元個數為P=Nθ×Nβ。假設場景中有一個點相對于雷達參考中心的方位角與俯仰角為θS和βS,那么發射和接收的等效天線輻射方向圖可以表示成F(θS,βS,t),后向散射系數可以表示成σ(θS,βS),那么雷達得到接收場可以表示為

(5)

式中：S表示整個目標場景。將整個目標場景按照上述規則離散化,可以得到:

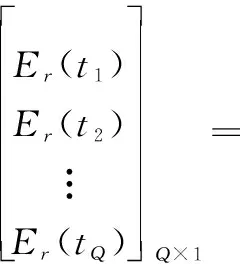
(6)

即

Er=Fσ

(7)

式中：Q表示采樣次數；tq為第q次離散采樣時刻(q=1,2,…,Q)；Er是各個離散時刻的采樣信號所組成的向量；σ是離散化場景后每個單元的等效后向散射系數所組成的向量,即待恢復場景圖像；F是各個離散時刻的離散化場景后每個單元對應的等效天線輻射方向圖的值所組成的矩陣,即場景圖像的采樣矩陣。

由于需要滿足輻射場在時間上的非相關性,采樣次數Q一定小于場景網格劃分的總的單元個數P,即矩陣F是個非滿秩矩陣。為了求解式(7)這個欠定問題,采用了稀疏約束將其轉化為一個非線性優化問題:

(8)

對于式(8),只需令矩陣成像網格的單元大小小于瑞利孔徑分辨極限,再通過優化的方法解出式(8)就可以得到超分辨成像的結果。

基于壓縮感知的超分辨關聯成像算法的大致流程如圖2所示。

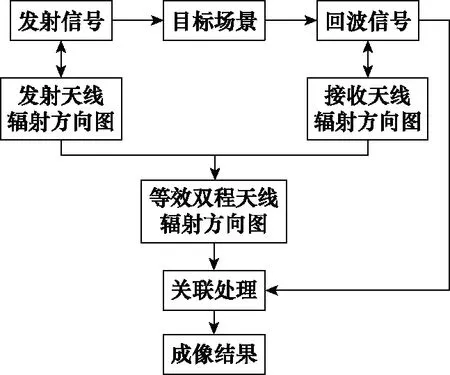
圖2 關聯成像算法流程圖Fig.2 Flow chart of correlated imaging algorithm

3.2 改進的基于壓縮感知的超分辨關聯成像算法

首先,考察載頻不變的單頻信號(如果只是二維成像就不需要引入線性調頻項來提高距離向的分辨率,這里也是方便說明)的基頻回波:

(9)

再來看一下步進頻信號的基頻回波:

(10)

(11)

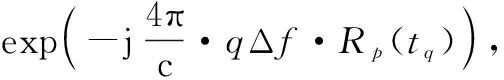
(12)

其中,矩陣F是一個Q×P的矩陣,其元素如下所示:

(13)

這樣的操作讓采樣矩陣F多了一個由于載頻變動導致的相位,剛好與等式左邊由于信號頻率步進導致的相位對應,即使等式平衡了,相當于完成了對于頻率變動的補償,之后對于式(12),加入稀疏約束后求解其最優解即可完成成像工作。

通過上面的補償,本質上是還原了式(6)左右兩邊的等式平衡,因為由于信號載頻步進的影響,導致了式(6)左邊的回波信號多了誤差相位,并且誤差相位耦合在回波信號之中,不方便直接補償將其剔除。而式(6)等號右邊的矩陣卻與之前載頻不變的時候毫無變化，即信號載頻步進的影響導致了式(6)等式的左右兩邊失衡。本文提出的補償方法正是補償了式(6)等式的右邊,左邊回波有多余的誤差相位,在右邊也加上相對應的誤差相位,使等式再度平衡。此為本文誤差補償的核心思想。

等式(6)經過補償以后成為式(12),即載頻變動情況下的式(12)與載頻不變情況下的式(6)是等價的。而正常情況(即載頻不變的情況)下,對式(6)進行最優化求解即可得到成像結果,故在載頻變動的情況下,對式(12)進行同樣的最優化求解自然也可以得到成像結果,后續的第5節采用了Matlab仿真,分析了本文補償方法的有效性和可行性。

圖3展示了改進的基于壓縮感知的超分辨關聯成像算法流程,總體流程和圖2基本一致,只是參與關聯處理的等效雙程天線輻射方向圖這一部分添加了相應的補償相位,這樣的改動使得由于載頻變化而累計在回波信號當中的誤差相位與等效雙程天線輻射方向圖中的補償相位剛好平衡。

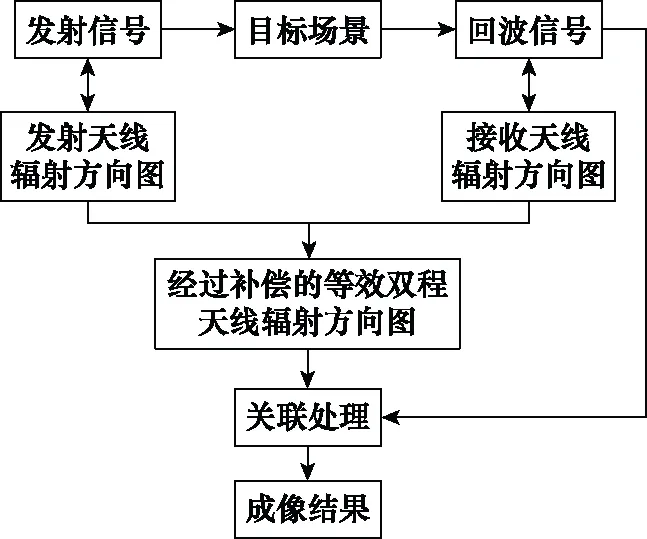
圖3 經過改進的關聯成像算法流程圖Fig.3 Flow chart of improved correlation imaging algorithm

4 仿真結果以及分析

本仿真實驗的仿真參數如表1所示。

表1 仿真參數

仿真的場景如圖4所示在距離雷達5 000 m的位置設置了5個目標點:(0,0),(10,10),(10,-10),(-10,10),(-10,-10),單位為m。

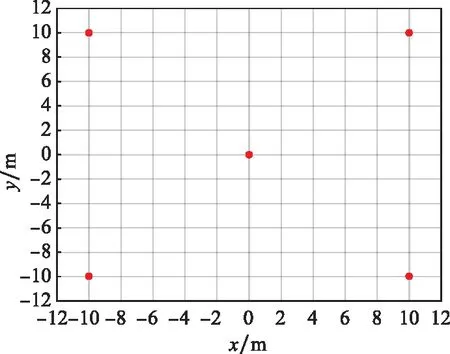
圖4 仿真場景圖Fig.4 Simulation scene diagram

采用頻率步進信號并用改進后的算法仿真，得到的結果如圖5和圖6所示。從圖5的結果上看，每個仿真的散射點都計算出來了,而且位置都可以和仿真場景對應上。為了凸顯出頻率變動無法成像,圖6給出兩張沒有補償頻率變動所造成的影響的仿真圖像，目的是為了說明如果沒有補償誤差相位將不能夠進行成像,強行使用關聯成像算法解出來的結果具有隨機性,沒有任何的規律可言。

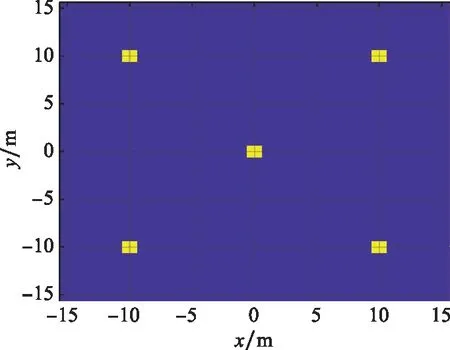
圖5 改進后的仿真圖Fig.5 Improved simulation image

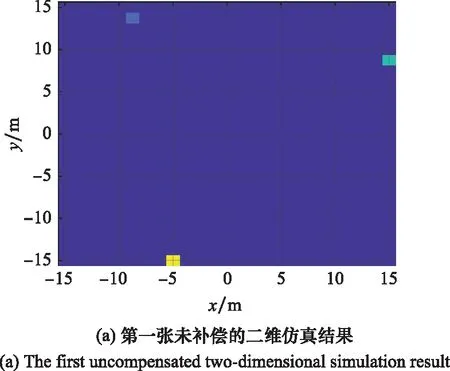
從圖6可以看到,仿真出來的圖像散射點是散亂的,并且是空間隨機的,每次仿真都會出現在不同的位置,甚至連散射點個數也不能夠確定。從這里也可以看到,對于頻率變動的補償是必不可少的。

以上的仿真實驗證明了本文的方法可以補償信號載頻變動產生的相位誤差,即本方法適用于信號載頻變動的情況。若信號載頻不變,則補償的相位exp(-j4π/c·qΔf·Rp(tq))中Δf這一項等于0,即本方法也同樣適用于信號載頻不變的情況。本方法就是對超分辨關聯成像的改進,使得其能夠在信號載頻變動的情況下正常運行。故本方法最好是用于需要信號載頻變動的情況,正常的信號載頻不變的情況下,不建議使用本方法。因為正常情況下,未改進的超分辨關聯成像本來就可以正常成像,而改進后的方法由于多了補償的相位計算,會增加計算量,降低運算速度,得不償失。

通過仿真實驗證明,此方法同樣適用于三維成像,由于三維成像除了方位、俯仰這兩個維度外,還增加了距離維度。而要在距離維上能夠產生足夠的分辨率就需要線性調頻信號,這里可以考慮一種載頻變化的線性調頻信號以配合這種超材料天線,達到三維成像的目的。仿真實驗使用的信號為載頻步進的線性調頻信號。

仿真參數和上一個實驗一致,只是仿真場景是一個三維的場景,通過仿真實驗來對其成像。

仿真場景如圖7所示,其中z軸方向即雷達視線方向。z軸的0點處距離雷達5 000 m遠,在z軸上的0,-5,5三處所在的與oxy平行的平面上均布置了4個點,這4個點的oxy坐標均為(10,10)(10,-10)(-10,10)(-10,-10),單位為m。

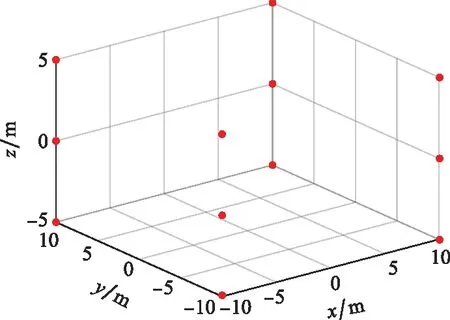
圖7 三維仿真場景圖Fig.7 Three-dimensional simulation scene diagram

如圖8可以看到和二維成像一樣,如果不補償頻率變動的影響,就無法成像。同樣給出兩張未補償圖像,其目的是為了說明如果沒有補償誤差相位將不能夠進行成像,強行使用關聯成像算法解出來的結果具有隨機性,沒有任何的規律可言。采用同樣的辦法補償多余的相位后可以正常成像,仿真圖像如圖9所示。

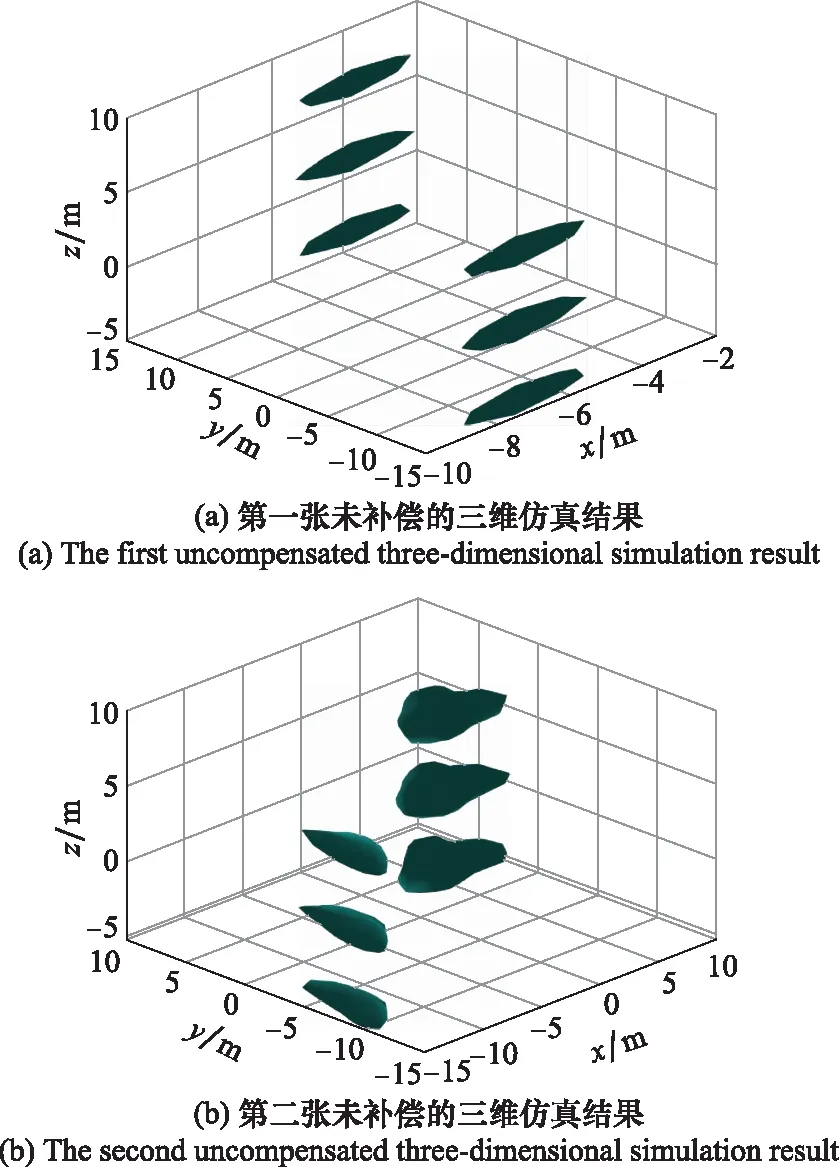
圖8 兩張未補償的仿真成像圖Fig.8 Two uncompensated simulation imaging images

圖9 經過補償后的仿真成像圖Fig.9 Simulated imaging images after compensation

可以看到,類似于二維成像,三維成像仿真所成圖像的散射點均能與仿真所設場景一一對應即達到了預期結果,驗證了所提方法的正確性。

5 結 論

本文提出一種基于壓縮感知的超分辨關聯成像算法的改進方法，將基于壓縮感知的超分辨關聯成像算法和超材料天線結合在一起,實現了低系統復雜度、低成本、高分辨率的微波關聯成像。本文通過設計仿真實驗證實了所提改進方法的正確性,并且驗證了此方法對于二維和三維成像均可以處理。這種改進方法通過一個小小的改變使成像算法可以結合超材料天線進而發揮出超材料天線的優勢。此方法并沒有提高原有算法的計算速度,對原有算法的改動比較小。因此,對于此算法仍有一定的提升空間。