基于FMCW雷達(dá)的旋轉(zhuǎn)目標(biāo)微動(dòng)參數(shù)提取方法

馮維婷, 梁 青, 谷 靜

(西安郵電大學(xué)電子工程學(xué)院, 陜西 西安 710121)

0 引 言

在雷達(dá)目標(biāo)中有一類是旋轉(zhuǎn)目標(biāo),比如無人機(jī)旋翼的旋轉(zhuǎn),彈道中段目標(biāo)的自旋、錐旋,這一類目標(biāo)除質(zhì)心平動(dòng)以外內(nèi)部旋轉(zhuǎn)的局部運(yùn)動(dòng)稱為微動(dòng)[1-3]。無人機(jī)處于懸停狀態(tài)時(shí)的微動(dòng)特征是識(shí)別目標(biāo)或干擾的重要依據(jù),彈道中段目標(biāo)的自旋、錐旋特征也是區(qū)別于誘餌和欺騙干擾的重要特征。因此,對(duì)旋轉(zhuǎn)目標(biāo)微動(dòng)特征的提取分析一直是雷達(dá)目標(biāo)識(shí)別領(lǐng)域的研究熱點(diǎn)[4-5]。

雷達(dá)目標(biāo)的微動(dòng)會(huì)調(diào)制雷達(dá)回波相位,使得目標(biāo)主體平動(dòng)引起的多普勒頻率周圍產(chǎn)生調(diào)制邊帶,這是微多普勒效應(yīng)[6]。對(duì)微多普勒參數(shù)的提取方法中,文獻(xiàn)[7-8]采用參數(shù)化提取方法,基于目標(biāo)的微動(dòng)特征構(gòu)造包含若干個(gè)參數(shù)的解調(diào)算子對(duì)信號(hào)進(jìn)行解調(diào),若干個(gè)參數(shù)在多維平面上進(jìn)行搜索,當(dāng)合適的參數(shù)構(gòu)成的解調(diào)算子與信號(hào)匹配時(shí)解調(diào)信號(hào)能量最大,從而通過搜索峰值進(jìn)行目標(biāo)微動(dòng)參數(shù)的估計(jì)。參數(shù)化方法是多維搜索方法,參數(shù)估計(jì)精度取決于搜索步長(zhǎng),高精度的參數(shù)估計(jì)值必然有巨大的運(yùn)算量。

微多普勒頻率具有時(shí)變特征,大量的文獻(xiàn)利用時(shí)頻分析方法處理這類非平穩(wěn)信號(hào)。文獻(xiàn)[9]對(duì)時(shí)頻分布結(jié)果采用經(jīng)驗(yàn)?zāi)Ｊ椒纸夥椒▽r(shí)頻曲線分解成若干獨(dú)立曲線來估計(jì)目標(biāo)的微動(dòng)參數(shù),但經(jīng)驗(yàn)?zāi)Ｊ椒纸夥椒ù嬖谀Ｊ交殳B問題,無法有效處理復(fù)雜的雷達(dá)信號(hào)。文獻(xiàn)[10]計(jì)算信號(hào)的時(shí)頻分布,基于時(shí)頻脊線分離出各散射點(diǎn)的時(shí)頻曲線來取得目標(biāo)微動(dòng)參數(shù),然而存在相互交疊處的時(shí)頻脊線提取錯(cuò)誤問題。為了解決多條時(shí)頻曲線相互交疊難以提取的問題,文獻(xiàn)[11]結(jié)合時(shí)頻分布與逆Radon變換進(jìn)行微動(dòng)參數(shù)估計(jì),逆Radon變換需要提前知道時(shí)頻曲線的周期,文中采用自相關(guān)法進(jìn)行周期估計(jì),但自相關(guān)法適合單分量信號(hào),無法有效估計(jì)多分量的信號(hào)周期。

針對(duì)以上問題,以旋轉(zhuǎn)目標(biāo)微動(dòng)參數(shù)提取為研究對(duì)象,利用德州儀器公司的60 GHz頻段調(diào)頻連續(xù)波(frequency modulated continuous wave, FMCW)毫米波小型雷達(dá)系統(tǒng)IWR6843搭建實(shí)驗(yàn)平臺(tái),進(jìn)行旋轉(zhuǎn)目標(biāo)雷達(dá)實(shí)測(cè)數(shù)據(jù)的采集。從FMCW雷達(dá)接收到的回波信號(hào)出發(fā),分析了旋轉(zhuǎn)目標(biāo)微多普勒信號(hào)特征、利用奇異值比譜、時(shí)頻分析和逆Radon變換相結(jié)合的方法進(jìn)行雷達(dá)采集數(shù)據(jù)的分析,完成了旋轉(zhuǎn)目標(biāo)微動(dòng)參數(shù)的有效估計(jì)。

1 FMCW雷達(dá)微動(dòng)參數(shù)特征分析

1.1 雷達(dá)信號(hào)模型

雷達(dá)發(fā)射寬帶線性調(diào)頻信號(hào),在一個(gè)調(diào)頻周期內(nèi),發(fā)射信號(hào)的解析表達(dá)式為

(1)

式中:t表示一個(gè)調(diào)頻周期TC內(nèi)的快時(shí)間;AT表示信號(hào)振幅;fc表示信號(hào)載波頻率;K表示信號(hào)調(diào)頻斜率。經(jīng)時(shí)延τ后,雷達(dá)接收的回波信號(hào)表示為

(2)

式中:AR表示接收信號(hào)振幅;時(shí)延τ=2d/c,其中d表示雷達(dá)與目標(biāo)之間距離,c表示光速。

sR(t)與sT(t)混頻處理,再經(jīng)過低通濾波器,得到的中頻信號(hào)表示為

sIF(t)=AIFexp[j2π(fcτ+fIFt)]

(3)

式中:AIF表示中頻信號(hào)振幅;fIF表示中頻信號(hào)頻率;fIF=Kτ。fIF與距離d的關(guān)系為

(4)

式中:B表示信號(hào)帶寬。由于TC很小,一個(gè)TC內(nèi)的距離近似為常量,因此對(duì)式(3)進(jìn)行頻域分析估得fIF,再利用式(4)可以得到目標(biāo)距離。

FMCW雷達(dá)連續(xù)發(fā)射多幀信號(hào),每幀有多個(gè)線性調(diào)頻信號(hào),對(duì)多幀中頻信號(hào)需要考慮目標(biāo)運(yùn)動(dòng)引起的多普勒現(xiàn)象,離散化后的多幀中頻信號(hào)可以表示為

sIF(n,m)=AIF(n,m)·exp{j2π[fIFn+fd(m)n)]}

(5)

式中:n表示快時(shí)間離散序列,長(zhǎng)度為N;m表示慢時(shí)間離散序列,長(zhǎng)度為M;fd是距離變化引起的多普勒頻率。

為了獲取旋轉(zhuǎn)目標(biāo)的微動(dòng)參數(shù),對(duì)式(5)在每個(gè)TC進(jìn)行脈沖壓縮,脈沖壓縮結(jié)果中目標(biāo)所在距離單元對(duì)應(yīng)的M點(diǎn)信號(hào)就是包含多普勒頻率的雷達(dá)多普勒信號(hào)。

1.2 旋轉(zhuǎn)目標(biāo)微動(dòng)特征分析

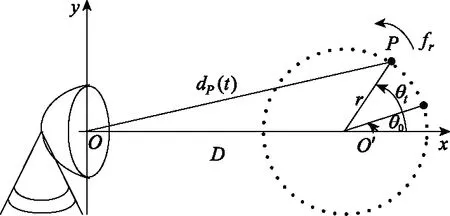
圖1 雷達(dá)與旋轉(zhuǎn)目標(biāo)幾何關(guān)系示意圖Fig.1 Diagram of geometrical relationship between radar and rotating target

當(dāng)旋轉(zhuǎn)目標(biāo)滿足遠(yuǎn)場(chǎng)條件,即(r/D)2→0,雷達(dá)與旋轉(zhuǎn)散射點(diǎn)P的距離可近似為

dP(t)≈D+rcos(2πfrt+θ0)

(6)

對(duì)式(6)求導(dǎo)得目標(biāo)速度為v(t)=d/dt[dP(t)]=-2πrfrsin(2πfrt+θ0)。根據(jù)fd的定義,旋轉(zhuǎn)目標(biāo)的微多普勒頻率可以表示為

(7)

式中:λ為載波波長(zhǎng)。

由式(7)可見,旋轉(zhuǎn)散射點(diǎn)P的微多普勒頻率是隨時(shí)間按正弦規(guī)律變化的曲線。正弦曲線的頻率就是目標(biāo)的旋轉(zhuǎn)頻率fr,初始相位就是散射點(diǎn)P在觀測(cè)初始時(shí)刻的相位θ0,振幅即是最大微多普勒頻率,該值由旋轉(zhuǎn)半徑、旋轉(zhuǎn)頻率和載波波長(zhǎng)共同決定,包含了目標(biāo)的結(jié)構(gòu)信息。一般情況下繞固定中心旋轉(zhuǎn)的散射點(diǎn)有多個(gè),它們具有相同的旋轉(zhuǎn)頻率fr、不同的旋轉(zhuǎn)半徑和初始相位,Q個(gè)旋轉(zhuǎn)散射點(diǎn)的多普勒頻率可以表示為

(8)

可以看出,同一旋轉(zhuǎn)中心的多個(gè)散射點(diǎn),其微動(dòng)特征表現(xiàn)為微多普勒頻率是一組頻率相同的正弦信號(hào)的疊加,各正弦信號(hào)的振幅和初始相位不同。因此,旋轉(zhuǎn)目標(biāo)微多普勒頻率中各正弦信號(hào)振幅、頻率和初始相位3個(gè)參數(shù)的提取是檢測(cè)和識(shí)別不同旋轉(zhuǎn)目標(biāo)的基本依據(jù)。

2 微動(dòng)參數(shù)提取方法

根據(jù)第1節(jié)結(jié)論,旋轉(zhuǎn)目標(biāo)微動(dòng)參數(shù)包括旋轉(zhuǎn)頻率fr、初始相位θ0和包含在最大微多普勒頻率中的旋轉(zhuǎn)半徑r。為了提取微動(dòng)參數(shù),采用的方法主要有3部分:基于奇異值比譜的旋轉(zhuǎn)頻率估計(jì)、時(shí)頻分析技術(shù)和利用逆Radon變換的振幅和初始相位估計(jì)。

2.1 基于奇異值分解的旋轉(zhuǎn)頻率估計(jì)

雷達(dá)脈沖壓縮后的多普勒信號(hào)表示為s(m),m=1,2,…,M。用信號(hào)s(m)構(gòu)造矩陣A,其表達(dá)式表示為

(9)

式中:Mj、Mi是正整數(shù),Mj·Mi≤M。對(duì)A進(jìn)行奇異值分解[13]

A=UDVT

(10)

式中:U為Mj階矩陣,U的列為A·AT的正交特征向量;V為Mi階矩陣,V的列為AT·A的正交特征向量;D為Mj×Mi的對(duì)角矩陣,對(duì)角線上前z個(gè)非零元素稱為奇異值,表示為σi(i=1,2,…,z)。

實(shí)際上基于式(9)構(gòu)造的矩陣A存在假設(shè)周期與實(shí)際周期之間的截?cái)嗾`差不斷積累的問題,常常無法有效估計(jì)頻率。受到周期信號(hào)奇異值分解特點(diǎn)的啟發(fā),改進(jìn)矩陣A的構(gòu)造方法。重新構(gòu)造的矩陣A為

(11)

式中:Mk=[k·fPRF/fri],符號(hào)[·]表示取整,fri是旋轉(zhuǎn)頻率在一定估計(jì)范圍內(nèi)進(jìn)行搜索的第i次值,搜索范圍表示為[frmin,frmax];L=[fPRF/fri]。

對(duì)每一個(gè)fri,進(jìn)行式(11)構(gòu)造的矩陣A的奇異值分解,計(jì)算奇異值比譜SVR(fri),旋轉(zhuǎn)頻率估計(jì)范圍[frmin,frmax]的峰值處對(duì)應(yīng)頻率就是fr的估計(jì)值。

2.2 基于同步壓縮變換的時(shí)頻分析

時(shí)頻分析技術(shù)是分析非平穩(wěn)信號(hào)的有利工具,可以得到微多普勒頻率隨時(shí)間變化規(guī)律。這里采用同步壓縮變換(synchro-squeezing transform,SST)的時(shí)頻分析技術(shù)。SST以短時(shí)傅里葉變換(short time Fourier transform,STFT)為基礎(chǔ)計(jì)算信號(hào)的線性時(shí)頻譜,再進(jìn)行壓縮,最后輸出分辨率高于STFT的時(shí)頻譜[15-16]。信號(hào)s(t)的STFT定義為

(12)

式中:g(τ-t)代表隨t移動(dòng)的窗函數(shù)。用一定長(zhǎng)度的窗函數(shù)g截取信號(hào)s(t),對(duì)截取信號(hào)進(jìn)行傅里葉變換得到t時(shí)刻信號(hào)的局部頻譜信息。隨著窗函數(shù)g沿整個(gè)時(shí)間軸的移動(dòng),就得到了信號(hào)在整個(gè)時(shí)間-頻率軸上的完整頻譜分布。

對(duì)于諧波信號(hào)sk(t)=ej2πfkt,經(jīng)STFT后的時(shí)頻譜能量集中在以頻率值fk為中心的一定頻帶寬度內(nèi),并且其兩側(cè)的時(shí)頻系數(shù)隨著與fk的距離增大而減小。由于窗函數(shù)的截?cái)嘈?yīng),信號(hào)的時(shí)頻譜存在模糊,時(shí)頻分辨率較低。

為了提高時(shí)頻分辨率,SST基于STFT進(jìn)行瞬時(shí)頻率fI(t,f)的估計(jì)[17],表達(dá)式為

(13)

(14)

2.3 基于逆Radon變換的微動(dòng)參數(shù)提取

對(duì)旋轉(zhuǎn)目標(biāo)的多普勒信號(hào)進(jìn)行時(shí)頻分析,微多普勒頻率表現(xiàn)為時(shí)頻譜圖中多條同頻率的正弦曲線的疊加,各曲線之間相互交疊。傳統(tǒng)的微多普勒參數(shù)提取方法是通過檢測(cè)時(shí)頻譜的能量峰值,提取出各條時(shí)頻脊線完成參數(shù)估計(jì),但是相互交疊的曲線在交叉點(diǎn)處容易檢測(cè)到錯(cuò)誤曲線,導(dǎo)致方法失效。為了解決時(shí)頻曲線難以提取的問題,根據(jù)旋轉(zhuǎn)目標(biāo)微多普勒頻率的正弦形式特點(diǎn),采用逆Radon變換提取正弦信號(hào)的振幅和初始相位兩個(gè)參數(shù)。

逆Radon變換能對(duì)時(shí)頻譜圖中的正弦曲線進(jìn)行能量積累、聚焦,將微動(dòng)參數(shù)估計(jì)問題轉(zhuǎn)化為逆Radon變換后參數(shù)空間中的峰值檢測(cè)問題。

旋轉(zhuǎn)散射點(diǎn)P的微多普勒頻率重新寫成如下形式:

fd(l,θ)=δ(l-lPsin(θ+θ0))

(15)

式中:lP是正弦信號(hào)的振幅,與式(7)的對(duì)應(yīng)關(guān)系為lP=4πrfr/λ,即最大微多普勒頻率;θ是隨時(shí)間變化的旋轉(zhuǎn)相位,θ=2πfrt。

時(shí)頻平面上fd(l,θ) 的逆Radon變換[19]為

g(x,y)=

(16)

式中:kx=ηcosθ;ky=ηsinθ。

Q個(gè)散射點(diǎn)逆Radon變換結(jié)果為

(17)

由式(17)可知,時(shí)頻平面上的一條正弦曲線經(jīng)逆Radon變換后是x-y參數(shù)空間中的一個(gè)點(diǎn)(xi,yi),該點(diǎn)對(duì)應(yīng)于正弦曲線的振幅lPi和初始相位θ0i。lPi與θ0i估計(jì)值與點(diǎn)坐標(biāo)(xi,yi)的關(guān)系為

(18)

進(jìn)行逆Radon變換前需要已知各正弦曲線的周期,其值根據(jù)上文中改進(jìn)的奇異值比譜方法得到。

綜上,多個(gè)散射點(diǎn)的微動(dòng)參數(shù)估計(jì)具體算法過程如下:

步驟 1將接收到的雷達(dá)中頻信號(hào)存放為二維數(shù)據(jù)矩陣形式,每行是一個(gè)調(diào)頻周期的N點(diǎn)快時(shí)間信號(hào),每列是M個(gè)調(diào)頻周期構(gòu)成的慢時(shí)間信號(hào)。

步驟 2對(duì)快時(shí)間維進(jìn)行脈沖壓縮得到距離維信息,抑制靜止目標(biāo)、干擾和噪聲,取出旋轉(zhuǎn)目標(biāo)所在的若干個(gè)距離單元并進(jìn)行相加,得到目標(biāo)慢時(shí)間維的M點(diǎn)多普勒信號(hào)。

步驟 3用多普勒信號(hào)構(gòu)造矩陣A,并進(jìn)行奇異值分解,見式(10)和式(11),基于奇異值比譜并搜索峰值估計(jì)旋轉(zhuǎn)頻率fr。

步驟 4對(duì)多普勒信號(hào)計(jì)算SST時(shí)頻譜,對(duì)時(shí)頻譜圖進(jìn)行逆Radon變換,估計(jì)最強(qiáng)目標(biāo)分量的旋轉(zhuǎn)半徑和初始相位。

步驟 5利用估計(jì)值構(gòu)造最強(qiáng)分量信號(hào),將其從原多普勒信號(hào)中剔除。

步驟 6重復(fù)步驟4和步驟5,直到估計(jì)出所有分量信號(hào)參數(shù)為止。

算法的處理流程如圖2所示。

圖2 算法流程圖Fig.2 Flow chart of the proposed algorithm

3 實(shí)驗(yàn)結(jié)果

3.1 仿真分析

選取3個(gè)旋轉(zhuǎn)散射點(diǎn)進(jìn)行仿真,雷達(dá)波長(zhǎng)為0.005 m;多普勒信號(hào)的振幅為1;散射點(diǎn)的旋轉(zhuǎn)頻率為4.5 Hz;各散射點(diǎn)的旋轉(zhuǎn)半徑為r1=0.10 m,r2=0.15 m,r3=0.20 m;初始相位為θ01=0.780 rad,θ02=2.870 rad,θ03=4.970 rad。設(shè)置高斯白噪聲下多普勒信號(hào)的信噪比(signal to noise ratio,SNR)為0 dB。

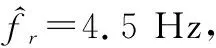
圖3 奇異值比譜Fig.3 Singular value ratio spectrum

多普勒信號(hào)的STFT和SST時(shí)頻譜如圖4所示。

由圖4可以看出,時(shí)頻譜中3個(gè)旋轉(zhuǎn)散射點(diǎn)微多普勒頻率為標(biāo)準(zhǔn)的正弦曲線形式,各曲線相互交疊,曲線的頻率相同,振幅和起始相位不同。圖4(a)的STFT時(shí)頻譜時(shí)頻聚集性較差,頻率分辨率較低。圖4(b)的SST時(shí)頻譜譜線清晰,時(shí)頻分辨率較高。

圖5 逆Radon變換結(jié)果Fig.5 Inverse Radon transform

采用所提方法在SNR分別為-6 dB、-3 dB、0 dB、3 dB、6 dB時(shí),各進(jìn)行100點(diǎn)蒙特卡羅實(shí)驗(yàn),得到旋轉(zhuǎn)頻率的估值均為4.5 Hz, 3個(gè)散射點(diǎn)的旋轉(zhuǎn)半徑和起始相位平均估計(jì)值見表1和表2。由表1和表2可以看出,各參數(shù)估計(jì)誤差隨著SNR的增加而減小,并且在強(qiáng)噪聲環(huán)境下所提方法仍能得到旋轉(zhuǎn)半徑和起始相位的高精度估計(jì)值。

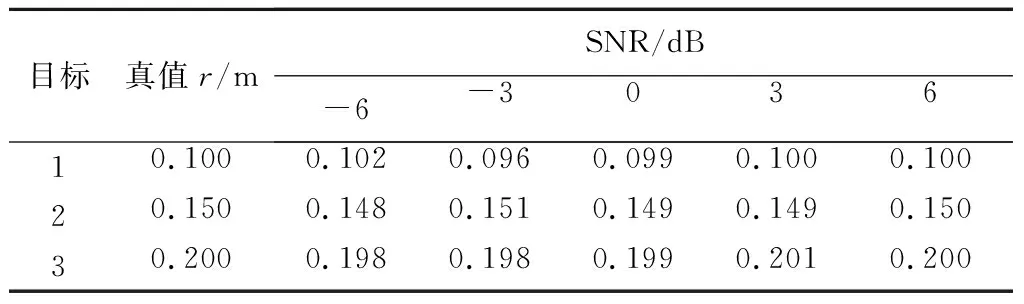
表1 旋轉(zhuǎn)半徑估計(jì)值

表2 起始相位估計(jì)值

3.2 實(shí)測(cè)實(shí)驗(yàn)

實(shí)測(cè)實(shí)驗(yàn)使用的FMCW雷達(dá)是德州儀器公司的IWR6843毫米波雷達(dá)系統(tǒng),配置了DCA1000高速數(shù)據(jù)采集卡,采用1發(fā)4收模式采集信號(hào)。試驗(yàn)中雷達(dá)參數(shù)設(shè)置如下:載波頻率fc=62.5 GHz,采樣頻率FS=2 MHz,調(diào)頻斜率K=25.998 MHz/μs,一幀數(shù)據(jù)包含128個(gè)調(diào)頻周期數(shù),調(diào)頻周期TC=240 μs,一個(gè)調(diào)頻周期內(nèi)的采樣點(diǎn)數(shù)為256點(diǎn),實(shí)際帶寬B=3.328 GHz,脈沖重復(fù)頻率為3 200 Hz。

實(shí)測(cè)實(shí)驗(yàn)裝置如圖6所示,設(shè)置的轉(zhuǎn)臺(tái)中心與雷達(dá)之間的距離約1.2 m, 旋轉(zhuǎn)半徑約0.14 m,兩個(gè)旋轉(zhuǎn)目標(biāo)的相位差為π rad。

圖6 實(shí)驗(yàn)裝置Fig.6 Experimental devices

接收到的雷達(dá)中頻信號(hào)中取一幀數(shù)據(jù),首先對(duì)每個(gè)調(diào)頻周期的256點(diǎn)快時(shí)間信號(hào)進(jìn)行脈沖壓縮得到一維距離像,再對(duì)一幀數(shù)據(jù)的128個(gè)調(diào)頻周期數(shù)據(jù)在慢時(shí)間維進(jìn)行傅里葉變換得到距離-多普勒像。一幀實(shí)測(cè)數(shù)據(jù)的距離-多普勒像如圖7所示。

圖7 一幀數(shù)據(jù)距離-多普勒像Fig.7 Range-Doppler imaging of one frame’s data

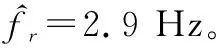
圖8 奇異值比譜Fig.8 Singular value ratio spectrum

對(duì)實(shí)測(cè)實(shí)驗(yàn)數(shù)據(jù)進(jìn)行SST變換,時(shí)頻分析結(jié)果如圖9所示。

圖9 旋轉(zhuǎn)目標(biāo)SST時(shí)頻譜Fig.9 SST time-frequency spectrum of rotating targets

圖9的時(shí)頻譜中是兩條相位相反的正弦曲線,這與圖6的實(shí)驗(yàn)設(shè)置相符。圖中零多普勒頻率對(duì)應(yīng)的轉(zhuǎn)盤主體能量大于兩個(gè)散射點(diǎn)的能量,不利于微動(dòng)參數(shù)提取。對(duì)多普勒信號(hào)求導(dǎo)處理,消除強(qiáng)零頻干擾,而兩個(gè)散射點(diǎn)的微多普勒頻率波形基本不受影響,求導(dǎo)處理后的時(shí)頻譜如圖10所示。

圖10 求導(dǎo)處理后的SST時(shí)頻譜Fig.10 SST time-frequency spectrum after calculation of derivation

實(shí)測(cè)實(shí)驗(yàn)數(shù)據(jù)的逆Radon變換結(jié)果如圖11所示。

圖11 逆Radon變換結(jié)果Fig.11 Inverse Radon transform

圖11中逆Radon變換結(jié)果存在展寬現(xiàn)象,這是因?yàn)閳D10中的時(shí)頻曲線并非理想等幅的標(biāo)準(zhǔn)正弦曲線的緣故。

2個(gè)旋轉(zhuǎn)目標(biāo)的微動(dòng)參數(shù)平均估計(jì)值見表3。實(shí)際旋轉(zhuǎn)目標(biāo)的初始相位和旋轉(zhuǎn)頻率未知,但從表3的旋轉(zhuǎn)半徑估值與真值的對(duì)比可以看出旋轉(zhuǎn)半徑的估值與真值基本符合;雖然初始相位未知,但是2個(gè)旋轉(zhuǎn)目標(biāo)的相位差是確定的,相位差的估值與真值也基本符合;旋轉(zhuǎn)頻率的估值是其他微動(dòng)參數(shù)估計(jì)的基礎(chǔ),其他微動(dòng)參數(shù)的有效估計(jì)間接表明了旋轉(zhuǎn)頻率估值的有效性,因此所提方法能有效估計(jì)實(shí)際雷達(dá)旋轉(zhuǎn)目標(biāo)的微動(dòng)參數(shù)。

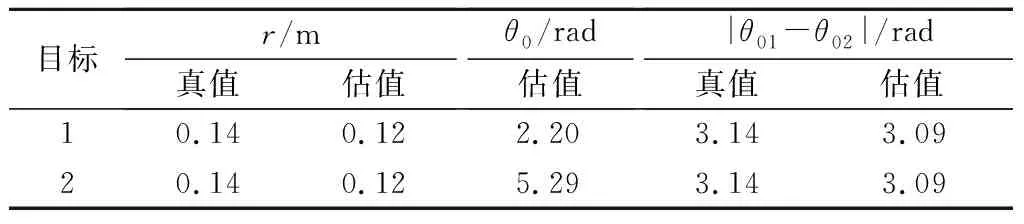
表3 實(shí)測(cè)數(shù)據(jù)微動(dòng)參數(shù)估計(jì)值

4 結(jié) 論

以旋轉(zhuǎn)目標(biāo)為研究對(duì)象,基于FMCW雷達(dá)推導(dǎo)了其多普勒信號(hào)的解析形式,并根據(jù)信號(hào)時(shí)頻譜的正弦曲線特征,提出了綜合利用奇異值比譜、SST時(shí)頻分析技術(shù)和逆Radon變換以提取旋轉(zhuǎn)目標(biāo)微動(dòng)參數(shù)的方法。仿真分析和雷達(dá)實(shí)測(cè)數(shù)據(jù)的實(shí)驗(yàn)結(jié)果表明,所提方法能有效提取旋轉(zhuǎn)目標(biāo)旋轉(zhuǎn)頻率、旋轉(zhuǎn)半徑和初始相位值,算法抗干擾能力強(qiáng),參數(shù)估計(jì)精度較高,所得的微動(dòng)參數(shù)為后繼的雷達(dá)目標(biāo)分類、識(shí)別、監(jiān)測(cè)打下了基礎(chǔ),也為復(fù)雜背景中復(fù)雜雷達(dá)目標(biāo)微動(dòng)特征分析提取提供了一種途徑。