基于節點重要度與改進信息熵的裝備體系效能評估方法研究

魏東濤, 劉曉東, 李 鵬, 陳玉金

(1. 空軍工程大學裝備管理與無人機工程學院, 陜西 西安 710051;2. 空軍勤務學院航材四站系, 江蘇 徐州 221000)

0 引 言

裝備體系作戰效能評估是軍力評估和裝備發展論證中的重難點問題之一,也是國內外軍事領域研究的熱點之一。隨著系統科學、復雜網絡理論的不斷發展,其在效能評估中的應用也日益廣泛。文獻[1]提出了基于整體效果的體系作戰效能評估方法,從整體作戰效果、靈敏度分析、裝備貢獻度、基于價值等效分析、任務完成情況等不同的視角對體系作戰效能進行評估分析。文獻[2-3]基于復雜網絡理論,分別提出“兩層四級”效能測度模型、“兩級五層” 網絡化效能評估模型,文獻[4]基于復雜網絡理論,提出了裝備體系作戰環建模方法。

在裝備作戰體系中,信息作為裝備關聯的關鍵載體,直接影響體系作戰效能的發揮,信息熵可用來衡量作戰過程不確定程度,文獻[5]將體系內裝備之間的信息流分為:態勢流、狀態流、指控流3類,通過對體系中信息流過程和傳遞函數的分析,構建了武器裝備體系效能模型,文獻[6-8]將作戰環理論、信息熵理論相結合,用于分析與評價體系作戰能力、作戰效能、體系貢獻度。

通過分析裝備體系網絡建模與效能評估的研究現狀,主要發現以下兩個問題。

(1) 基于作戰環進行建模時,大多從網絡局部特征參數對節點展開研究,沒有從網絡全局視角對節點重要度進行評估,不能反映各節點的層次結構關系。

(2) 在體系效能計算時,大部分研究忽略了裝備自身屬性和戰時生存力對作戰效能的影響,體系效能評估不夠全面。

針對以上分析,本文建立了一種基于節點重要度與改進信息熵的體系作戰效能分析模型。首先,基于作戰環理論和裝備分層思想,構建包含多功能裝備的作戰環網絡模型。其次,考慮網絡拓撲結構、裝備靜態狀態和作戰態勢的影響,從網絡全局、網絡局部和戰時裝備完好性3個視角對節點重要度進行分析。然后,將節點權值引入體系效能計算,改進了信息熵效能評估方法。最后,以轟炸藍方指揮所作戰體系為例,說明該方法的應用與合理性。

1 基于作戰環的裝備體系網絡建模

1.1 節點建模

現代戰爭循環理論認為完整的作戰過程是集OODA(observation、orientation、decision、action)于一體的循環過程。基于OODA環理論,文獻[4]提出了作戰環概念,將己方裝備體系抽象出的偵察類、指控類、影響類節點與對方目標類節點構成標準作戰環。在建模過程中,默認體系內裝備功能單一,但隨著科學技術的不斷進步,作戰裝備通常具有兩種或兩種以上的功能,如多用途戰斗機兼具偵察與打擊功能,若簡單將其抽象為某一類節點,則對其評價不夠全面。因此,采用裝備分層思想,按照“裝備-功能”層級映射,對裝備進行功能分解,如圖1所示。多功能型裝備按照偵察、決策、攻擊功能分解成若干功能模塊,各功能模塊用作戰環邊鏈接,采用裝備分層映射方法對裝備體系網絡建模,單一功能裝備抽象為該功能對應的功能模塊,多功能裝備可以抽象為若干虛擬裝備模塊節點,使得裝備網絡建模更加貼合實際情況。

圖1 裝備的分層描述Fig.1 Layered description of equipment

同一類節點中的不同裝備,由于性能指標存在差異,裝備作戰能力也不盡相同,為了區分不同裝備的作戰能力,為方便下文建模,根據OODA環節點定義, 參考已有的指標體系[9-12], 本文構建的節點能力指標體系如圖2所示。

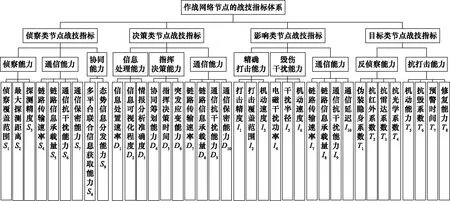
圖2 節點能力指標體系Fig.2 Node capability index system

1.2 邊的建模

由于信息流傳輸具有方向性,作戰環節點之間主要有偵察(T-S)、決策(S-D)、指揮(D-I)、打擊(I-T)、信息共享(S-S)、協同指揮(D-D)等6種信息關聯關系,分別對應6種作戰環邊。

邊的作戰效能水平與所連接的兩個節點的戰技指標及關聯關系有關,可以用邊的任務需求隸屬度函數進行表示:

Eij=f((xi1,xi2,…,xin),(xj1,xj2,…,xjm),Ok)

(1)

式中：Eij∈[0,1],表示邊的作戰效能對任務需求的滿足能力；xi1,xi2,…,xin表示節點vi的戰技指標；xj1,xj2,…,xjm表示節點vj的戰技指標；Ok表示邊所屬邊關系類型,k∈{T-S,S-D,D-I,I-T,S-S,D-D}。

任務需求隸屬度函數一般通過體系建模仿真、統計分析、規則推理、專家經驗等方式建立。

在實際作戰過程中,由于不同裝備的功能類別、技術先進程度、面臨的作戰態勢存在較大差異,對體系作戰效能的貢獻程度不盡相同。在網絡模型中,裝備重要性映射為節點在網絡中的關鍵程度,因此在初始化網絡時,應按照節點的功能屬性、結構屬性、作戰屬性賦予相應的權重,其中,功能屬性可以用邊的任務需求隸屬度進行表示。

2 節點重要性分析

2.1 基于解釋結構模型的節點網絡全局重要性分析

解釋結構模型(interpretation structure model,ISM)是最早由美國沃費爾德教授于1973年提出的一種結構模型化分析方法[9],該方法是在圖論的基礎上,按重構的思想對系統建模,獲得系統直觀、整體層次的結構關系,廣泛應用于關鍵要素辨識[10]、結構層次劃分[11]等方面。

作戰環網絡節點的分類抽象以及裝備體系本身具有的層次結構,決定了作戰網絡也具有層次結構特征[12]。因此,本文采用ISM形式化方法對體系網絡結構進行描述,通過分析節點之間相互影響關系,實現作戰環網絡向層次結構轉化,從網絡全局的角度分析節點的重要程度,如圖3所示。

圖3 作戰環網絡層次劃分示意圖Fig.3 Schematic diagram of hierarchy division of operation loop network

采用ISM對作戰環網絡層次結構劃分,首先對標準作戰環進行等效變換,將目標節點分為源點T?和匯點Tθ兩個虛擬節點,如圖4所示。

圖4 作戰環網絡的等價變換示意圖Fig.4 Schematic diagram of equivalence change of operation loop network

作戰環網絡進行等價變換后,使用等價鄰接矩陣A′=[aij]N×N表示體系結構,若裝備實體(功能模塊)vi與裝備實體(功能模塊)vj相關聯,則aij=1,否則aij=0,且aii=0。將等價鄰接矩陣A按照節點類型劃分為分塊矩陣:

式中：VS、VD、VI分別表示作戰環網絡中的偵察類、指控類、影響類的節點集；V?T、VθT表示目標類節點的源點集和匯點集；Ass表示信息共享關系；ASD表示決策關系；ADD表示協同指揮關系；ADI表示指揮關系；AIT θ表示毀傷打擊關系；AT ?S表示偵察關系。

采用ISM方法對作戰環網絡結構層次劃分的具體步驟如下。

步驟 1構建作戰環網絡等價鄰接矩陣A′。

步驟 2求解可達矩陣M，表示為

M=(A′+I)1≠(A′+I)2≠…(A′+I)r=(A′+I)r+1

(2)

式(2)是對矩陣A′+I進行冪布爾運算。

步驟 3對可達矩陣M進行級別劃分,繪制多級遞階圖。構建節點vi的可達集合R(vi)和先行集合B(vi)如下:

R(vi)={vj|mij=1}，j=1,2,…,n

(3)

B(vi)={vj|mji=1}，j=1,2,…,n

(4)

式中：R(vi)表示節點vi通過有向信息流可以影響的節點集合；A1(vi)表示通過有向信息流可以影響節點vi的集合。進行節點等級劃分,繪制多級遞階有向圖的判斷條件如下：

R(vi)∩B(vi)=R(vi)

(5)

式中：R(vi)∩B(vi)表示可達集合和先行集合的交集,當R(vi)∩B(vi)=R(vi),表示節點集中的其他節點能夠影響節點vi,而vi不能影響其他節點。

步驟 4層級權重，設通過層級劃分,作戰環網絡包含n個層級Li′(i′=1,2,…,n),定義節點vi的層級權重為

(6)

式中:i′表示節點vi所處的層級。

令βi表示與vi相關聯的節點集合對vi的影響程度,計算公式定義如下:

(7)

式中:λ為入度節點系數,通常取λ>0.5[10-11],表示節點出度的重要性小于入度；bk→i表示與vi相關聯的入度節點的網絡層級權重；ck→i表示與vi相關聯的入度節點的數量；bi→j表示與vi相關聯的出度節點的網絡層級權重；ci→j表示與vi相關聯的出度節點的數量。

步驟 5確定節點的網絡全局權重,綜合節點本身所處的層級權重和與該節點相關聯節點的影響,定義節點的網絡全局權重為

(8)

2.2 基于復雜網絡的節點局部重要度分析

網絡參數是作戰體系特征的定量表現,體現了網絡結構的拓撲特征[13-14],通常情況,常用節點度數是衡量節點脆弱性,但是單一指標很容易加大網絡薄弱環節預測的不準確性[15]。因此,本文采用節點度、節點效率等參數來衡量節點的重要性。

定義節點強度ki的計算表達式為

(9)

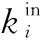
節點效率η是指節點vi與網絡中其他節點之間距離的倒數之和的平均值[16],節點效率越高,表明該節點向其他節點傳輸信息越容易,在網絡中的地位越重要,計算表達式為

(10)

式中:N為網絡節點數量。若節點vi到節點vi不存在連通的路徑,則dij=∞,ηij=0。

綜合vi自身節點強度和對其他節點的影響度,定義節點vi的網絡局部權重為

(11)

(12)

(13)

單一功能裝備權重是其對應節點權重,多功能裝備權值為其對應多節點權值之和。

2.3 基于模糊評判法的戰時裝備完好性分析

節點功能的發揮是建立在各裝備(功能模塊)完好的基礎上,參照效能評估ADC模型中可用性概念,戰時裝備完好性可以表示為裝備(功能模塊)在某一作戰任務期間能夠使用且完成規定功能的能力,裝備完好性越高,表明裝備完成任務的可能性越高,該裝備抽象的網絡節點越重要。

該意義下,戰時裝備完好性可分為兩部分:裝備自身靜態的可靠性,以及裝備在敵方威脅下的生存力,兩部分數值的乘積為戰時裝備完好性水平。

裝備可靠性一般通過平均故障間隔時間(mean time between failure, MTBF)、作戰時長t來計算,在不考慮維修性和延遲時間的情況下,裝備可靠性計算公式為

(14)

由于體系對抗環境的復雜性,影響裝備生存的因素有很多,不僅與己方因素有關,還受敵方武器和客觀戰場環境的制約,使得裝備生存力評估具有明顯的模糊性。因此,本文采用模糊評判法對裝備生存力進行評估。計算步驟如下。

步驟 1確定評價對象因素集U。在預設的作戰條件下,通過裝備作戰態勢信息分析、專家經驗等方式獲得影響裝備生存力的因素集U:

Ui={xi1,xi2,…,xin}

(15)

式中:xij表示影響裝備i生存力的第j個元素。

步驟 2確定評價對象評語集Pi和定量評價數值集Hi。將評價結果劃分為若干個等級的評語集,一般情況下,取3～5個等級,對應的定量評價值在[0,1]內。

步驟 3確定各因素權值。本文采用改進層次分析法(improved analytic hierarchy process, IAHP)方法對因素權值賦權。與標準層次分析法相比,IAHP可省略一次性檢驗環節,具有更強的適應性[17]。利用IAHP確定權重的一般步驟為

步驟 3.1建立三標度判斷矩陣。

對同一層次上的影響因素進行兩兩比較,采用三標度法進行量化,具體含義如表1所示。

表1 三標度量化法

得到判斷矩陣C的表達式為

步驟 3.2構建傳遞矩陣Z，矩陣中第i行j列元素為

(16)

步驟 3.3構建擬優化傳遞矩陣G，矩陣中第i行j列元素為

gij=exp(zij)

(17)

步驟 4單因素評價。

利用專家組評價結果,構建因素集Ui到評語集Pi的模糊評價關系矩陣Ri:

式中：rij表示第i個影響因素屬于第j級評語的隸屬度,可以根據專家評價結果得到。

步驟 5多指標綜合評價。

利用式(17)計算裝備i生存力的各評語的隸屬程度：

Ti=Riξi′T

(18)

利用式(18)將裝備i的隸屬度矢量轉換為裝備生存力值：

(19)

(20)

綜上,將節點的網絡權值和戰時完好度的乘積定義為節點權值,計算公式為

(21)

3 基于改進信息熵的體系效能計算

由于戰場環境和裝備作戰的不確定性,作戰環網絡中各節點、邊所代表的裝備(功能模塊)、作戰活動具有較大的不確定性,本文將節點權值賦予概率意義,節點權值越大,則表示節點完成任務的可能性越大。

信息熵可以反映信息的不確定性,因此可以通過信息熵表征作戰體系效能。目前,基于信息熵的效能評估僅考慮節點功能對效能的影響,缺少對節點網絡適應性和生存力對效能影響的分析,效能評估結果可信度較低。因此,本文將節點權值引入到信息熵模型中。

3.1 作戰效能模型

假設邊的任務需求的隸屬度為Eij(0≤Eij≤1),可以用自信息量-lnEij來度量該邊效能發揮帶來的不確定性,考慮節點權重對作戰效能的影響,則該邊的綜合自信息量為

(22)

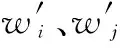
作戰環的不確定自信息量為各邊綜合自信息量之和,計算表達式為

(23)

式中:m,n分別為作戰環中信息共享邊和協同指揮邊的數量。

作戰環的效能為

Eop=exp(-Hop)

(24)

作戰環網絡中,多個作戰環同時包含同一作戰目標,將環之間的關系看作電路中的并聯關系,假設包含作戰目標Ti的作戰環數量為y(y=2,3,…),第j個作戰環的不確定性自信息量為Hij,針對作戰目標Ti的不確定自信息量為

(25)

針對單目標的作戰體系效能為

Ei=exp(-Hi)

(26)

針對多個作戰目標的作戰體系效能為

(27)

式中:wi為作戰目標權重。

3.2 作戰效能評估流程

基于節點重要度與改進信息熵的體系作戰效能評估評估流程如圖5所示。

圖5 體系作戰效能評估流程圖Fig.5 Flowchart of system operation effectiveness evaluation

體系效能的評估步驟如下。

步驟 1基于作戰環理論與裝備分層方法對裝備體系網絡建模。

步驟 2根據作戰環網絡等價鄰接矩陣,采用ISM和復雜網絡理論確定節點網絡全局權重。

步驟 3采用模糊評判法對裝備戰時完好性進行評,并計算節點權重。

步驟 4根據節點權重和邊的任務需求隸屬度值,計算作戰環自信息量。

步驟 5依據目標權重和作戰環數量,計算裝備體系作戰效能。

4 案例分析

4.1 轟炸藍方指揮所作戰體系模型構建

該體系典型的作戰想定為紅方的偵察衛星(S1)、預警機對藍方攔截飛機(T1)、藍方指揮所(T2)的態勢信息進行偵察,經通信衛星(S4)傳回地面指控中心(D2),經過信息處理后向戰斗機,地空導彈(I4)下達命令,打擊藍方攔截飛機,使藍方失去制空能力,然后向轟炸機(I2),地地導彈(I3)下達轟炸藍方指揮所的命令,以完成預定作戰任務,作戰時長為6 h。

根據紅藍雙方武器裝備構成,抽象為作戰網絡模型,如圖6所示,由于預警機兼具偵察和指控功能,在網絡中抽象為節點S2和D1。戰斗機兼具偵察和打擊功能,在網絡中抽象為節點S3和I1。

圖6 轟炸藍方指揮所作戰網絡模型Fig.6 Combat network model for bombing the blue side logistics bases

4.2 節點網絡權重計算

(1) 作戰網絡模型等價變換,構建等價鄰接矩陣。

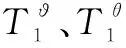
圖7 作戰網絡等價模型Fig.7 Equivalent model of combat network

等價鄰接矩陣A′為

(2) 根據式(1),得到可到矩陣M:

(3) 根據分級原理,對網絡節點進行層級劃分。

第1次計算得出該作戰網絡的各節點的可達集R(vi)和先行集B(vi)以及兩者交集如表2所示。

表2 第一級分解結果

根據表2中數據,確定第1層級節點的集合L1={Tθ1,Tθ2},本文因篇幅有限,層級計算過程略。經計算,該作戰環網絡可劃分為7個層級,分別為第1層級L1={Tθ1,Tθ2},第2層級L2={I1,I2,I3,I4},第3層級L3={D2},第4層級L4={D1},第5層級L5={S2,S3,S4},第6層級L6={S1},第7層級L7={T?1,T?2},

(4) 建立解釋結構模型

根據層次劃分結果重新排列可達矩陣,可建立相應的ISM解釋結構模型,如圖8所示。由于第7層級節點T?1、T?2,與第1～5層級的各元素都有相同的跨級關聯關系,僅與第6層級元素存在區別。

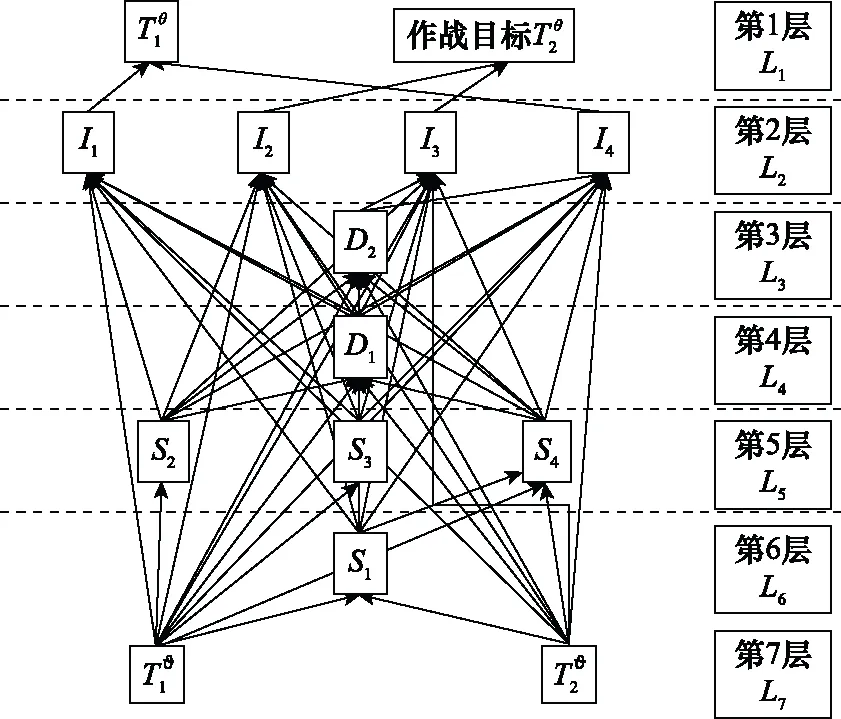
圖8 作戰網絡解釋結構模型Fig.8 Interpretation structure model of combat network

從圖8可以看出,利用解釋結構模型對作戰環網絡模型分析,獲得了作戰環網絡整體結構上的劃分,將各節點間的復雜關系層次化和條理化。該作戰環網絡不同層級間的節點關系錯綜復雜,相互關聯,解釋結構模型中的有向箭頭表明了各因素間的相互影響關系。第1層為作戰目標層,第2層是影響體系作戰效能的直接因素,包括影響類節點I1、I2、I3、I4,該層次節點作戰性能的優劣直接影響作戰任務完成效果,第2～4層級上的節點是影響體系作戰效能的間接因素,第6層級是全局影響因素,包含偵察類節點S1,該節點是裝備體系進行作戰的前提,其功能的波動不僅會影響偵察類節點作戰效能,也會影響其他層級因素的作戰效能。

(5) 計算節點網絡全局權重

根據式(6),各層級權重為

α=(0.385 7,0.192 8,0.128 6,0.096 4,

0.077 1,0.064 3,0.055 1)

令節點入度系數λ=0.6,根據式(7)和式(8)計算,得到各節點的網絡全局權重如表3所示。

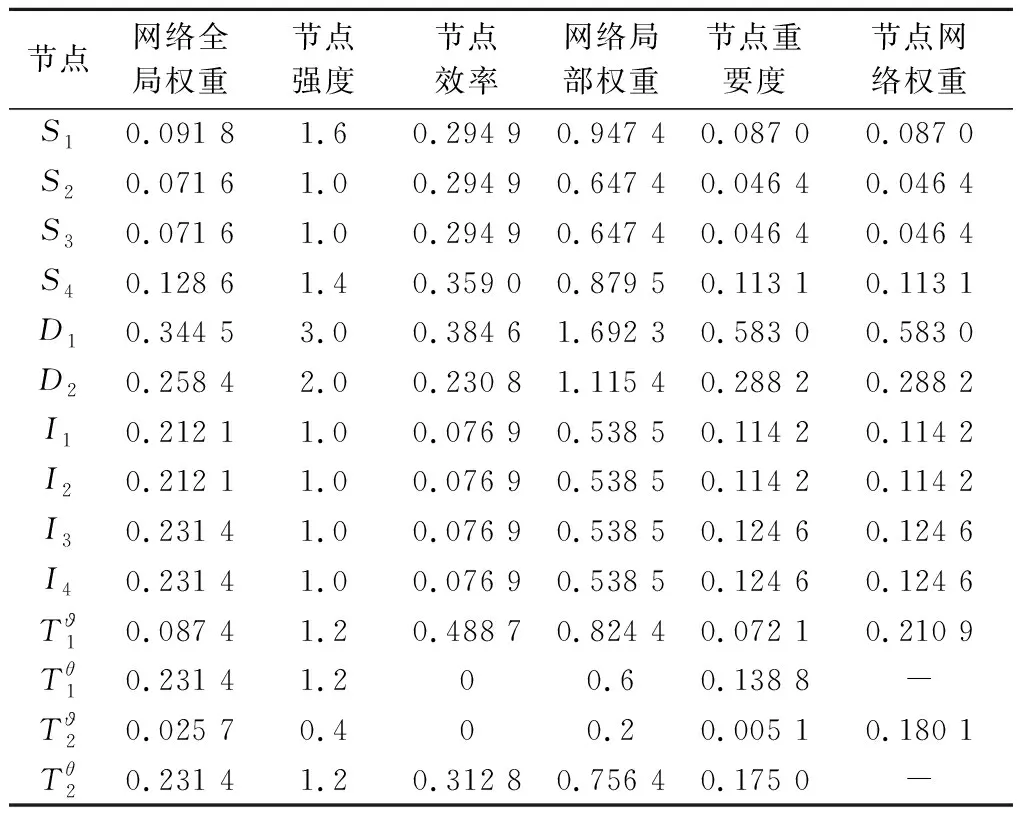
表3 節點各類權重

4.3 基于復雜網絡理論的節點局部權重計算

根據圖7中的作戰網絡模型,根據式(9)～式(13)分別計算節點強度、節點效率、節點網絡局部權重、節點重要度、節點權重等數值。由于將藍方攔截飛機(T1)、藍方指揮所(T2)分別抽象為兩個虛擬的作戰節點,該節點的權重為相對應虛擬節點的權重之和。計算結果如表3所示。

4.4 裝備戰時完好性評估

(1) 基于模糊評判法的裝備生存力分析

以戰斗機為例,采用模糊評判法計算裝備戰時裝備完好性,步驟如下。

步驟 1確定影響戰斗機生存力的因素集為

步驟 2確定評語集和評價值

定量評價數值為Hi=(1,0.75,0.5,0.25,0)。

步驟 3確定因素權重

采用改進層次分析法,得到三標度比較矩陣為

根據式(16)和式(17),經計算,歸一化的權重向量為

ξ′=[0.562 7,0.288 9,0.148 3]

步驟 4單因素評價

由20名專家對每個因素進行評價,統計每個因素評價等級的專家投票人數比例,得到評價矩陣:

步驟 5多指標綜合評價

C=ξ′R=[0.46,0.29,0.13,0.11,0.01]

裝備的生存力值為

E=CH=0.741 4

同理,可確定其他裝備的生存力權值,如表4所示。

(2) 裝備可靠性分析

計算各裝備的可靠性,平均無故障時間根據歷史數據或經驗給出,以預警機為例,在不考慮其戰時維修性的情況下,預警機的平均故障間隔時間為63 h,工作時長6 h的可靠性為:

E=exp(-6/63)=0.91

對于偵察衛星,運行環境比較穩定,平均故障間隔時間可達3 000 h以上,可認為其在工作6h的可靠性為1。對于其他類型裝備的可靠性數值如表4所示。

綜上,根據式(21)計算節點的權重,如表4所示。

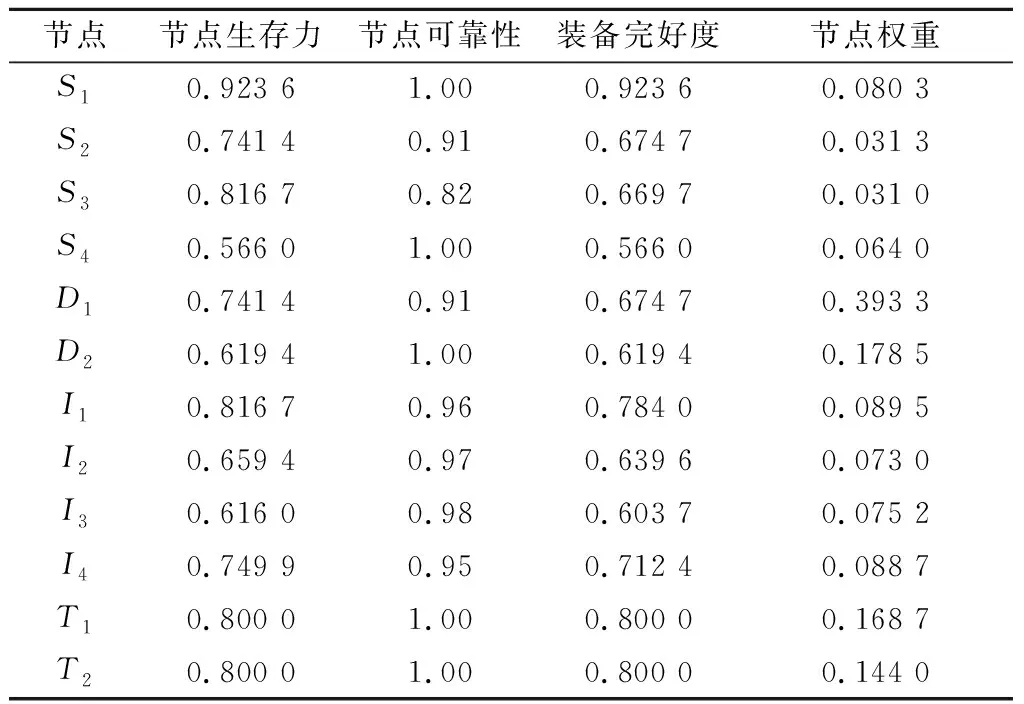
表4 裝備完好度及節點權重

4.5 基于作戰熵的體系效能分析

根據作戰體系中裝備戰技指標仿真結果,確定各邊的任務需求隸屬度,根據式(22)計算各邊的綜合信息量,如表5所示。

表5 作戰環網絡邊的自信息量

對圖6中作戰網絡的鄰接矩陣進行分析,包含目標節點TI、T2的作戰環數量分別為N(T1)=7,N(T2)=3,結合各邊的綜合自信息量，確定包含目標節點的作戰環及其不確定自信息量,如表6所示。

表6 目標節點作戰環及其不確定自信息量

經計算,打擊空中攔截飛機的效能為0.996 8,轟炸藍方指揮所的效能為0.990 9,若將目標的權重分別定位0.3和0.7,則該體系的作戰效能為0.992 7。

4.6 評價結果分析

在裝備作戰體系中,指控類裝備的重要度大于作戰裝備。針對本文想定案例,由表3和表4可以看出,預警機(D1)、地面指揮中心(D2)的網絡權重、節點權重均高于體系內其他裝備,結果符合裝備重要度比較的相關原則,表明應用ISM與復雜網絡理論對裝備重要度評估具有可行性。

針對現役裝備作戰體系,考慮戰時裝備完好性對作戰效能的影響,如果偵察類、指控類、影響類裝備戰時不能保證自身存在,則該裝備對體系貢獻度為0;如果作戰過程中裝備受到損傷,該裝備作戰效能會降低,同時導致經過該節點的作戰環的效能降低,則該裝備的重要性會被削弱。本文采用節點網絡權重與戰時完好性數值相乘來計算權重具有合理性。

考慮不同作戰對象對體系效能的影響,通過將作戰類目標與已方裝備按照關聯關系進行重要度評估,在信息熵計算時,將節點權重賦予概率意義,參與節點綜合自信息量計算,對體系效能的評估結果可信。

5 結 論

基于作戰環理論和裝備分層方法,將多功能裝備抽象為若干功能模塊進行網絡建模,即可以確保節點功能單一,又使得作戰網絡模型更加貼合作戰體系實際,通過對標準作戰環進行等效變換,基于ISM和復雜網絡理論對節點重要性進行分析,采用采用模糊評判法和改進層次分析法對裝備戰時生存力進行評估,提出了改進信息熵的體系效能評估方法。

本文所述方法是對裝備體系效能評估方法進行了補充和改善,可以用于分析比較不同條件下不同種類的體系效能,同時為軍力評估、裝備體系發展論證、裝備組合規劃打下堅實基礎。