變化海流環境下AUV能量最優三維路徑規劃

李亞南, 黃海濱, 陳亮名, 莊宇飛,*, 王曉麗

(1. 哈爾濱工業大學(威海)信息科學與工程學院, 山東 威海 264209;2. 南洋理工大學機械與航天工程學院, 新加坡 639788)

0 引 言

近年來,隨著海洋自主觀測和數據收集設備的需求增加,海洋資源呈現出巨大價值,海洋的勘探和開發也越來越受到關注[1]。作為水下勘探的主要工具之一,自主水下航行器(autonomous underwater vehicle, AUV)具備高度的自主性和靈活性[2]。AUV在執行許多水下任務時都發揮著重要作用,例如沿海生態系統數據收集[3-5]、掃雷[6-8]、海底勘測[9-11]、通信中繼[12-14]等。在上述任務背景中,AUV路徑規劃是最基本且最關鍵的問題之一[15]。因此,非常有必要研究AUV的路徑規劃問題。

對于AUV的路徑規劃問題,相關研究者提出了許多不同類型的算法,包括A*算法、快速探索隨機樹(rapidly-exploring random trees, RRTs)以及其他基于圖搜索的水下路徑規劃算法。A*算法將路徑規劃問題轉換為圖搜索問題,文獻[16]采用A*算法為滑翔機在海洋環境下規劃了運動路徑。雖然A*算法的執行效率高,但由于A*算法是一種啟發式的算法,其無法保證所規劃路徑的全局最優性。RRTs算法廣泛用于路徑規劃研究中,為了考慮航行器運動的方向性以及動態海流的影響,可以通過在RRTs中添加偏差的算法實現路徑規劃。盡管RRTs可以有效地對高維和非凸的空間進行搜索,但是其預測的路徑通常不是最優的[17]。此外,動態海流的影響通常不能準確地被并入到RRTs的計算公式中。因此,RRTs不能很容易地適用于高精度和存在海流下的水下路徑規劃。圖形搜索算法是在20世紀60～80年代之間提出的,已成功應用于許多實際任務中。然而,基于網格的圖搜索算法獲得的狀態是離散的,因此限制了AUV在運動過程中的航向[18]。

上述算法存在的不足是不能獲得全局最優路徑,并且在考慮海流對路徑規劃的影響時不夠精確。然而,很多應用需要獲得最優路徑,再加上海流廣泛存在于海底,忽略海流的影響可能使所獲得的結果難以應用于實際工程中。因此,考慮存在海流影響的情況下,開發既精確又有效的算法來規劃路徑并使所規劃的路徑滿足所設定的優化指標,是很有研究意義和價值的[19]。

目前,為了獲得航行器在水下環境影響下的最優路徑,部分研究已經取得了一些進展。文獻[20]采用并行群搜索算法研究了時變海流下的最優路徑規劃問題。Lolla等人在文獻[21]中提出了一種用于獲得水下最優運動路徑的算法,該算法可以準確地描述動態環境海流對航行器運動的影響。此外,這項工作也已擴展到如何獲得所需能量最少的路徑[22]。文獻[23]在多航行器任務分配的研究中,采用最優控制理論設計了一種海流影響下的路徑規劃算法。注意到,上述工作僅考慮了二維(two-dimensional, 2D)的運動環境,并將AUV的路徑限定在恒定水深下。然而,海流的大小通常會隨水深的變化而變化。因此,2D情況下的規劃算法不適用于不規則海床以及隨深度變化很大的復雜海流等三維(three-dimensional,3D)環境下的AUV運動規劃。

為了解決3D環境下的AUV運動規劃問題,有研究為了提高規劃效率并減少內存需求,將3D環境投影到2D空間。然而,由于海流和障礙物的存在,這樣投影得到的2D空間無法完全體現3D環境下的所有信息[24]。文獻[19]首次采用水平集算法解決完全適用于3D的海洋環境下AUV路徑規劃問題,但是并未將此工作擴展到能量最優路徑規劃。文獻[25]研究AUV實時最優路徑規劃問題時采用最優控制理論得到近似解析解,并在3D海流環境下產生近似最優路徑，但是此算法不適用于AUV的速度很低的情況。基于以上綜述可以得出,對3D下存在海流影響的AUV能量最優路徑規劃問題還有待進一步研究。

在上述相關工作的基礎上,本文首先對AUV提出了一種從起始位置行駛至目標位置的3D能量最優路徑規劃算法。通過該算法,可以獲得從起始位置到目標位置的能量最優路徑。其次,在這項工作中考慮了更加接近實際工程背景的變化海流的影響,即海流與位置成固定關系。最后,利用一般線性系統的狀態空間理論,得到了最優控制律的顯式解。與現有的迭代和離散算法(例如圖搜索和進化算法)相比,基于最優控制的算法可以在3D動態海流的影響下,可以生成能量最優路徑和速度控制律,并獲得全局最優路徑。由于本文研究的AUV運動模型為非線性,這對于求得最優解析解帶來了難度。

1 問題描述

1.1 運動學模型

考慮AUV的運動模型如圖1所示,定義慣性坐標系G-xyz和體坐標系O-xbybzb。在慣性坐標系中,G為坐標原點,Gx置于海平面,且指向地理正東方向,Gz指向地心。在體坐標系中,O為坐標原點,并固定在AUV的重心,Oxb軸選取在AUV的縱中剖面內,正向指向船首,Ozb垂直于水平面指向地心方向。慣性坐標系和體坐標系都遵循右手螺旋法則。

圖1 參考坐標系與AUV六自由度運動Fig.1 Reference coordinate system and six degrees of freedom movement of AUV

向量vc=[vcx,vcy,vcz]T用于描述慣性坐標系下的海流速度,假設海流大小僅隨G-xyz下的位置而變化。忽略側傾運動的影響,欠驅動AUV的運動學模型可以由以下方程表示:

(1)

1.2 問題定義

2 能量最優控制

(2)

定義相應的哈密頓函數為

(3)

(4)

(5)

(6)

由于式(5)和式(6)對于所有t≥t0滿足對時間求導等于0,所以可以分別得到：

(7)

(8)

由式(4)可得

(9)

將式(7)變形為

(10)

將式(8)變形為

(11)

整理式(10)和式(11)得

(12)

(13)

當滿足式(12)和式(13)時,AUV的運動滿足最小化性能指標J。注意到式(3)～式(13)采用最優控制理論的龐特里亞金極小值原理,對第1.2節所提出的問題,得到了全局最優解所需要滿足的條件。根據文獻[27]中定理4.1,若找到一組符合式(12)和式(13)的解,那么該解可以全局優化性能指標式(2)。

3 最優航速及初始導航角求解

(14)

(15)

(16)

進一步得到

(17)

(18)

將式(17)、式(18)以及海流向量代入式(1),得到:

(19)

(20)

可得初始時刻為t0，初始狀態為x(t0),y(t0),z(t0)時，其解為

(21)

式中：B=u*(0)I3，

首先求狀態轉移矩陣：

(22)

將B、T(t)以及xtf、ytf和ztf代入,求解上述線性定常系統非齊次方程，得到：

(23)

為了得到最優的運動路徑,最優航向和最優航速需分別滿足式(15)和式(16)。而式(15)和式(16)的求解則依賴于非線性代數方程式(23)。注意到非線性代數方程式(23)的已知參數是AUV的運動初始位置、末端位置和海流的大小。這就意味著最終能否順利求解得到最優航向和最優航速,以及求解得到的最優航向和最優航速能否物理實現,取決于所給定的AUV運動初始位置、末端位置和海流的大小。當所給條件過于苛刻,將面臨著最優航速、航向不可物理實現問題。

4 仿真驗證

4.1 仿真參數設置

以下是AUV在海流的影響下從給定起始點到終止目標點的連續能量最優路徑的仿真,選取起始時間t0=0,航行終止時間為tf,起始點(0,0,70),終止點為(70,80,0),海流向量vc=10-3[2x-y,x+2y,2z]T,此海流是變化的,表現為不同位置的海流大小是不同的,考慮到海流的穩定性,因此假設在一定時間內海流并不隨時間變化。

4.2 能量最優AUV路徑規劃仿真結果

4.2.1 海流影響下能量最優路徑規劃

首先進行第一種情況仿真,即AUV在海流下由起始點到終止點的能量最優路徑規劃仿真。給定AUV俯仰角θ=π/3,將初始條件、海流大小以及給定起始點和目標點代入到式(23)中,通過數值求解方法得到最優初始導航角、最優航速和航行終止時間,如下所示:

(24)

再將式(24)中計算所得u*(0)以及航行終止時間tf代入式(2)中求得所需能量消耗。在第4.1節中給定的仿真參數下,得到如圖2～圖4所示的仿真結果。圖2為海流影響下的AUV在x,y,z方向上的能量最優路徑,其中橫軸為航行終止時間,縱軸為AUV在x,y,z方向上的位移變化,仿真結果驗證了AUV在能量最優性能指標下能夠精確地到達目標位置。圖3為海流影響下基于最優控制的AUV航速及艏向角變化曲線,基于最優控制的能量最優路徑規劃所求速度保持恒定以及所求艏向角呈線性變化,因此可保持推進器的推力為常值,基于最優控制規劃的能量最優路徑更易物理實現。

圖2 海流影響下的AUV能量最優路徑Fig.2 Energy-optimal path of AUV in presence of ocean current

圖3 海流影響下基于最優控制的AUV航速及艏向角變化曲線Fig.3 Velocity and yaw angle changing curve of AUV based on optimal control in presence ocean current

圖4為海流影響下的3D AUV路徑,其中藍色實線是AUV由起始點到終止點的路徑,紅色箭頭表示海流。實驗結果驗證了基于最優控制的算法能有效解決AUV面向能量消耗的路徑規劃問題,在給定條件下獲得全局能量最優路徑。

圖4 海流影響下的AUV能量最優3D路徑Fig.4 Energy-optimal 3D AUV path in presence of ocean current

為說明基于最優控制優化算法的效果,用非優化的負反饋控制器進行仿真對比。第二種情況給出AUV采用負反饋控制器在海流下由起始點到終止點的路徑仿真。AUV運動學模型為式(1)所描述,海流變量仍為vc=10-3·[2x-y,x+2y,2z]T。

基于負反饋的路徑規劃的設計過程如下。首先設計輔助控制量:

(25)

式中：k0為正常數。由此得到負反饋控制器的運動過程及其控制變量：

(26)

將起始點和終止點代入,k0取0.03(k0>0均可),仿真結果如圖5所示。圖5為基于負反饋控制器的航速和艏向角以及俯仰角變化曲線,雖然其航速和艏向角均可物理實現,但是對比圖3和圖5,基于負反饋控制所求速度需實時變化,而基于最優控制的能量最優路徑規劃所求速度保持恒定以及所求艏向角呈線性變化,因此可以始終保持推進器的推力是一個常值,驗證了基于最優控制所規劃的能量最優路徑更易物理實現。

圖5 海流下基于負反饋的AUV艏向角、俯仰角及航速變化曲線Fig.5 AUV yaw angle, pitch angle and velocity changing curvebased on negative feedback under ocean current

圖6為基于負反饋控制器與基于最優控制的AUV能量消耗對比圖,基于負反饋控制能量消耗遠大于基于最優控制優化的路徑規劃所需能量消耗,因此驗證了基于最優控制的能量最優路徑規劃算法的優越性。為說明海流變化程度對所提優化算法的影響,接下來擴大海流大小,針對AUV在海流下從(0,0,70)到(70,80,0)的能量最優路徑規劃仿真。給定AUV俯仰角θ=π/3,得到最優航速、航行終止時間和能量,如表1所示。當海流為原始大小時,在起始點、終止點的海流大小分別為0.14 m/s和0.24 m/s,此海流的最大值為0.28 m/s,得到的航速為0.26 m/s。海流與AUV航速一般設置為同一量級大小[29],而AUV航速大小一般為0～10 kN,得到的航速小于AUV實際最大運行速度,因此算法在物理上可實現。

圖6 基于負反饋控制器與基于最優控制的AUV能量消耗對比圖Fig.6 Comparison of AUV energy consumption based on negativefeedback controller and optimal control

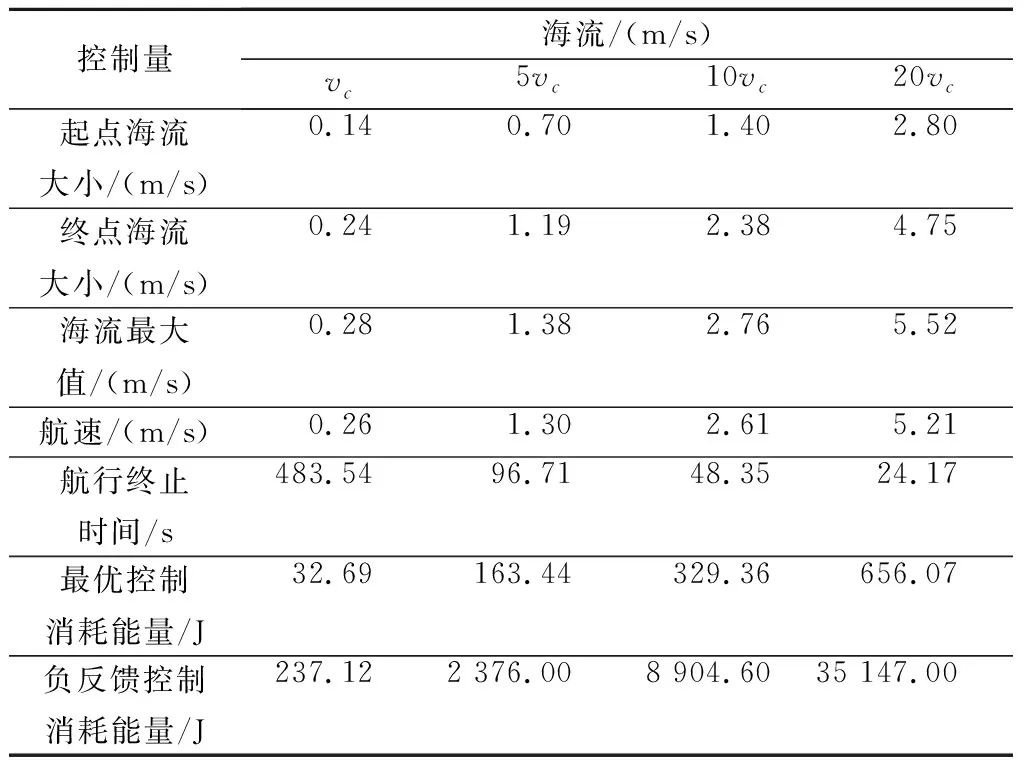
表1 不同海流下的控制量計算結果

海流分別擴大5倍、10倍時,得到的航速小于AUV實際最大運行速度,可以物理實現。

當海流擴大20倍時,即20vc=10-3[40x-20y,20x+40y,40z]T,在起始點、終止點的海流大小分別為2.8 m/s和4.75 m/s,此海流的最大值為5.52 m/s,得到的航速為5.21 m/s,得到的航速稍大于AUV的實際最大運行速度。因此當逆向海流過大時,導致所求航速過大,面臨著不可物理實現問題。為了驗證最優控制的可實現性問題,考慮當海流擴大100倍時,無法求得可行解,這是由于海流過大造成的。因此,當所給條件較苛刻時,將面臨著物理不可實現問題。

4.2.2 大深度情況下能量最優路徑規劃

為了面向海底管道檢修、掃雷以及水下傳感器網絡數據采集任務,需要大深度情況下的能量最優路徑規劃[30-31]。接下來進行AUV在海流下從(0,0,700)到(700,800,0)的能量最優路徑規劃仿真,驗證了本文所提出的能量最優路徑規劃算法同樣適用于大深度下的路徑規劃需求。并進行了在俯仰角分別為π/3 rad,π/4 rad,0.99 rad下的能量最優路徑規劃,仿真結果如圖7所示。

圖7 不同俯仰角下的3D AUV能量最優路徑Fig.7 3D AUV energy-optimal path at different pitch angles

圖7中藍色實線為θ=π/3 rad下的能量最優路徑,黃色實線為θ=π/4 rad下的能量最優路徑,紫色實線為θ=0.99 rad下的能量最優路徑。表2為不同俯仰角下最優航速、最優導航角和航行終止時間的計算結果。由表2看出，起始點和終止點相同的情況下,由于俯仰角不同,仿真結果不同。其中，在θ=0.99 rad下為連接起始點和終止點的俯仰角,但由于海流的原因,其所需的能量并不是最少的。在θ=π/4 rad下所求航速不可物理實現,且需要更多的能量,因此可以根據不同俯仰角下的計算結果,選取適當的俯仰角。

表2 大深度下不同俯仰角的控制量計算結果

接下來進行AUV在海流下從(0,0,700)到(700,800,0)的基于負反饋控制器的仿真。將起始點和終止點代入,得到所需能量消耗為7 759.4 J,其大于采用優化算法的能量消耗,因此驗證了此優化算法的優越性。基于負反饋控制器在大深度下的仿真結果如圖8所示,與基于最優控制的能量最優路徑規劃所求速度保持恒定以及所求艏向角呈線性變化,基于最優控制所規劃的能量最優路徑更易物理實現。接下來進行針對AUV在海流下從(0,0,700)到(700,800,0)的基于負反饋控制器的仿真。將起始點和終止點代入,得到所需能量消耗為7 759.4 J,其大于采用優化算法的能量消耗,因此驗證了此優化算法的優越性。基于負反饋控制器在大深度下的仿真結果如圖8所示,與基于最優控制的能量最優路徑規劃所求速度保持恒定以及所求艏向角呈線性變化,基于最優控制所規劃的能量最優路徑更易物理實現。

圖8 大深度下基于負反饋的AUV艏向角、俯仰角及航速變化曲線Fig.8 AUV yaw angle, pitch angle and velocity changing curve based on negative feedback under large depth

5 結 論

水下環境的復雜性是AUV路徑規劃的巨大挑戰,本文提出了一種3D環境下的AUV能量最優路徑規劃算法,采用了最優控制理論來得出最優航速變化律以及艏向角變化律,并考慮海流與水下位置成固定函數關系,獲得從初始位置到目標位置的能量最優路徑,能夠有效地克服海流對AUV路徑規劃的影響。最后通過仿真對比了多組不同參數情況下的最優路徑規劃過程,仿真結果表明基于最優控制的算法下AUV能夠精確地到達目標位置,驗證了基于最優控制的優化算法的有效性。此外,基于最優控制的算法有效減少能量消耗,且規劃的路徑更易物理實現。未來的工作將進一步研究更復雜的海洋環境情況,例如存在障礙物和更加復雜海流的對AUV路徑規劃的影響。此外,將進一步研究在有限能量以及時變、非線性海流情況下的路徑規劃問題。