雙指標階段性退化建模及可靠性分析
毛澤龍, 王治華,*, 吳 瓊, 劉成瑞
(1. 北京航空航天大學航空科學與工程學院, 北京 100083; 2. 北京空間飛行器總體設計部, 北京 100080;3. 北京控制工程研究所研發(fā)中心, 北京 100080)
0 引 言
目前,針對高可靠長壽命產品的可靠性分析,性能退化建模方法已廣泛應用。為簡化模型,早期研究大多在產品退化過程僅具備單一退化規(guī)律的前提下開展。工程實際中,一方面,產品自身物理機理或運行環(huán)境、負載情況等的動態(tài)變化,會導致退化過程呈現出兩階段甚至多階段的演變特點[1-3];另一方面,由于功能多樣性和組成復雜性,產品往往具有多個性能指標,且這些指標間存在耦合關系[4-6]。此時,單一指標單一階段的性能退化模型往往不能準確反映高可靠長壽命產品的真實退化規(guī)律。針對此類產品,如何建立合理退化模型準確描述多階段、多指標退化規(guī)律成為相關研究的熱點和難點。
針對單一指標多階段性能退化問題,基于隨機過程的方法能較好描述退化過程中由產品內部失效機理及外界環(huán)境因素導致的時變不確定性,已廣泛應用[7]。其中,Wiener過程由于能描述非單調退化過程以及良好的數學性質和物理解釋,應用最為普遍[8-9]。文獻[10]針對液力耦合器退化過程呈現先慢后快的特征,以振動幅值為性能指標,基于Wiener過程建立了兩階段退化模型。文獻[11]針對液力耦合器第一階段為單調退化,第二階段為非單調退化的特點,進一步提出了基于Gamma過程和Wiener過程的兩階段退化模型。文獻[12]針對電容器容量退化特征,建立三階段Wiener過程評估其可靠性。針對產品退化過程中存在的非線性規(guī)律,文獻[13]基于Wiener過程建立了兩階段非線性模型;文獻[14]進一步建立了發(fā)動機的多階段非線性退化模型。
針對多指標聯合退化問題,指標間相關性的合理描述至關重要。目前考慮指標相關性的建模方法主要有以下幾類:基于多維隨機過程(如多維Wiener過程)建模[15-18];將多指標融合為單一指標后建模[19-20];基于Copula函數的建模[4,21-29]。其中,基于多維隨機過程的建模方法適用于各指標退化規(guī)律相近的情況;對于第二種思路,融合原始指標后得到的新指標,難以明確其物理意義及相應失效閾值,限制了其應用范圍;而基于Copula函數的建模方法能夠有效克服以上問題,因此得到了廣泛應用。文獻[21]基于Wiener過程和Copula函數建立雙指標退化模型,各指標的邊緣分布通過Wiener過程描述,指標間的相關關系由Copula函數表征。文獻[22]進一步研究退化過程具有個體差異時的雙指標建模問題。文獻[23]以某型繼電器為研究對象,提出了基于Copula函數和Wiener過程的雙指標加速退化數據建模方法,并建立了基于貝葉斯馬爾可夫鏈蒙特卡羅的模型參數估計方法,擴充了雙指標退化模型的使用范圍。文獻[4,24-26]進一步針對指標數量更多的情況開展了研究。考慮到某些產品各指標退化過程是單調的,文獻[27-28]采用逆高斯過程和Copula函數建立雙指標退化模型。
綜上可見,以上有關階段性特征的研究均圍繞單一指標的退化過程展開,無法描述多指標聯合退化時的情況;有關多指標建模研究均未考慮指標退化的階段性特征,可能導致可靠度評估結果出現偏差。對于產品退化過程中耦合性與階段性規(guī)律并存時可靠性分析問題有待進一步研究。文獻[29]以飛機艙門鎖為研究對象,采用指標間相關性描述退化過程的耦合性,對退化過程同時存在耦合性與階段性的建模問題進行了探究。
本文通過Copula函數描述指標間相關性,引入變點描述退化階段性,考慮不同階段指標間耦合性規(guī)律變化,建立了雙指標階段性退化模型,并給出了可靠性評估方法。另外,針對退化過程包含兩個變點且不在同一位置,而難以估計的問題,提出了一種考慮雙指標變點的模型參數整體估計方法。最后,通過實例分析,驗證了本文方法的建模合理性與可靠性分析有效性。
1 退化規(guī)律分析與模型引出
工程實際中,一些產品退化過程呈現多指標和階段性規(guī)律并存的特點。例如,飛機艙門鎖[29]關鍵部分為連桿機構,連桿之間、連桿與基座間均通過軸和軸套連接,構成了多個連接點。在使用中,連接點軸套會逐漸磨損,當任一連接點軸套磨損量超出對應的失效閾值,則艙門鎖失效。通過對艙門鎖的失效機理和退化數據分析,發(fā)現其中兩處連接點軸套的磨損最為嚴重,將這兩處軸套的磨損量作為艙門鎖的兩個性能指標,記為指標1和指標2,其性能退化測試數據如圖1所示。

圖1 艙門鎖性能退化數據Fig.1 Degradation data of cabin door lock mechanism
從圖1中可見,指標1和指標2的退化呈現明顯的兩階段特征,這是由于前期潤滑劑充足,軸與軸套間潤滑良好,軸套磨損速率較慢;隨著潤滑劑消耗,當消耗到某一水平,軸套磨損速率迅速增大。同時需注意,指標1變點在0.2×105次運動循環(huán)附近,指標2變點在0.3×105次運動循環(huán)附近,兩指標變點不在同一位置。此外,由于艙門鎖的結構特點,兩連接點的磨損也相互影響,即指標1和指標2之間還存在耦合關系。
綜上可見,此類產品退化特點可總結如下:考慮產品具有兩個性能指標,令Xi(t)表示第i個指標的退化過程,其中i=1,2;當任一指標首次達到對應失效閾值時,則產品發(fā)生失效;兩指標退化過程均呈現階段性,且在很多情況下,不同階段內指標相關性強弱不一致(該結論將在實例分析中說明)。根據兩指標變點τ1、τ2間位置關系,問題可分為兩類:考慮最一般的情況,當τ1≠τ2時,不妨令τ1<τ2,變點τ1、τ2將產品退化過程分為3段:(0,τ1]、(τ1,τ2]、(τ2,+∞),各段內指標退化規(guī)律與耦合規(guī)律均可以不相同;當τ1=τ2時,產品退化過程為兩階段,可視為前述一般情況的簡化。
此類產品退化過程中耦合性和階段性規(guī)律并存,帶來了以下挑戰(zhàn):一是如何建立合理的退化模型表征退化過程中不同階段雙指標間耦合性規(guī)律;二是由于產品兩指標退化過程均包含變點,且兩變點不在同一位置,如何建立有效的模型參數估計方法;最后,由于退化過程復雜,可靠度解析形式難以獲得,如何基于退化模型有效評估產品可靠性。
2 雙指標階段性退化建模
2.1 邊緣退化建模

對于兩個性能指標均呈現兩階段退化規(guī)律的情況,對指標i,基于Wiener過程建立如下兩階段邊緣退化模型:
Xi(t)=[μi1Λi1(t)+σi1B(Λi1(t))]I(0,τi](t)+
[Xi(τi)+μi2Λi2(t-τi)+σi2B(Λi2(t-τi))]I(τi,∞)(t)
(1)
式中:τi為指標i的變點(即在時刻τi,指標i退化過程由第一階段進入第二階段);μi1和μi2分別為指標i第一和第二階段的漂移系數,表征各階段的退化速率;σi1和σi2分別為指標i第一和第二階段的擴散系數,表征各階段分散性;I(0,τi](t)、I(τi,∞)(t)為示性函數;B(·)為標準Wiener過程;Λi1(t)=tγi1、Λi2(t-τi)=(t-τi)γi2為第一和第二階段的時間尺度變換函數,分別表征指標i在各階段退化的非線性特征;指標i的邊緣退化模型參數可記為Θi=(μi1,μi2,σi1,σi2,γi1,γi2,τi),i=1,2。
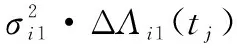
(2)
則退化增量ΔXij在變點τi前后服從不同參數的正態(tài)分布可表示為
(3)
退化增量ΔXij的累積分布函數和概率密度函數分別為
(4)
(5)
式中:Φ(·)為標準正態(tài)分布的累積分布函數。
2.2 基于Copula的雙指標階段性退化建模
根據常用假設[21],本文通過Copula函數描述指標間的相關性,在不同時間間隔內,指標1與指標2退化增量間的相關性可忽略,即僅考慮同一時間間隔內兩指標退化增量間的相關性;由此在邊緣退化模型基礎上,構建雙指標階段性退化模型。根據Sklar’s理論,兩指標退化增量ΔX1j、ΔX2j的聯合分布函數F(ΔX1j,ΔX2j)可由各自邊緣分布函數F1(ΔX1j)、F2(ΔX2j)和Copula函數表示,即
F(ΔX1j,ΔX2j)=C(F1(ΔX1j),F2(ΔX2j);θ)
(6)
式中:C(·)為Copula函數,表征指標退化增量間的相關關系;θ為Copula函數參數,與指標退化增量間的相關性大小有關。
兩指標的變點τ1、τ2將測試時間段分成了3段,考慮到各段內指標間的相關性大小可能不一致,θ在各段內取值也不相同,分別為θ1、θ2、θ3,即
θ=θ1I(0,τ1](tj)+θ2I(τ1,τ2](tj)+θ3I(τ2,∞)(tj)
(7)
針對兩個指標的情況,目前應用較廣的Copula函數有Gaussian Copula、 Gumbel Copula、Clayton Copula、Frank Copula等,這幾種Copula函數具有不同的耦合性描述效果。本文采用在退化領域已廣泛使用的Frank Copula函數描述指標增量間的耦合性。Frank Copula函數及其密度函數具體形式見文獻[30]。綜合考慮指標退化的階段性與指標間的相關性,建立雙指標階段性退化模型如下:
(8)
模型參數可記為Θ=(Θ1,Θ2,θ1,θ2,θ3)。
3 可靠性分析
確定模型參數估計值是利用雙指標階段性模型進行可靠性分析的前提。模型待估參數為Θ=(Θ1,Θ2,θ1,θ2,θ3)。由于參數較多,難以通過直接優(yōu)化對數似然函數獲得模型參數估計值,且模型參數中包含兩個變點,進一步給參數估計帶來困難。針對以上問題,本文提出了一種考慮雙指標變點的模型參數整體估計方法。
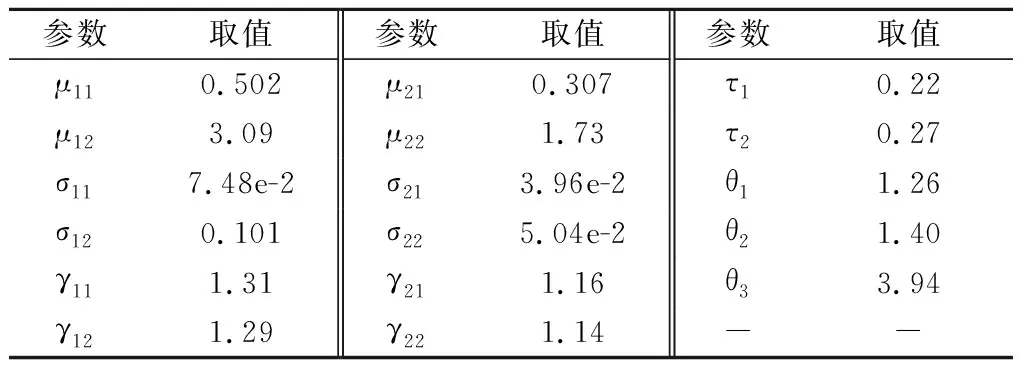
假設兩個性能指標的變點τ1、τ2分別位于測試時刻tw1、tw2(tw1 f(ΔX1j,ΔX2j)=c(F1(ΔX1j),F2(ΔX2j);θ)· (9) 式中:c(·)為Frank Copula函數對應的密度函數。 對于(t1,t2,…,tw1)時刻的測試數據,由式(9)得到同一時刻各指標退化增量的聯合密度函數為 (10) 進一步由不同時刻退化增量獨立,建立(t1,t2,…,tw1)時刻的退化數據的似然函數為 (11) 相應的對數似然函數為 (12) 類似地,(tw1+1,tw1+2,…,tw2)、(tw2+1,tw2+2,…,tn)時刻的測試數據的對數似然函數分別為 (13) (14) 綜上,由式(12)~式(14),m個試樣在時間段[t1,tn]的對數似然函數可表示為 lnL(Θ)=lnL1+lnL2+lnL3 (15) 建立對數似然函數后,根據以下步驟估計模型參數。 步驟 1定義如下關于tw1、tw2的函數。 log-LF(tw1,tw2)=lnL(Θ)max|τ1=tw1,τ2=tw2 (16) 式中:log-LF(tw1,tw2)為假定變點τ1、τ2位于測試時刻tw1、tw2時,對數似然函數lnL(Θ)的最大值。其中對lnL(Θ)的優(yōu)化基于遺傳算法實現,本文通過調用Matlab工具箱的ga函數優(yōu)化lnL(Θ)。 步驟 2確定tw1、tw2可能的取值組合。由于tw1、tw2滿足t1 步驟 3計算函數log-LF(tw1,tw2)在上述取值組合對應的值。取log-LF(tw1,tw2)最大時對應的取值組合作為變點估計值,對應的其他模型參數取值作為模型參數最優(yōu)估計。 得到模型參數估計值后,可結合退化模型及失效閾值計算產品可靠度。對于兩指標聯合退化的產品,當其任一指標退化量首次達到失效閾值時,即認為其發(fā)生失效。具體地,設產品兩指標對應失效閾值分別為D1、D2,產品可靠度可定義如下: (17) 由于產品退化過程復雜,可靠度的解析形式難以獲得,采用蒙特卡羅方法計算可靠度。蒙特卡羅方法的基本思想是應用隨機抽樣技術得到符合待求解分布的樣本,通過對樣本值的觀察與統計,實現對未知分布的分析。 根據雙指標階段性退化模型及模型參數估計值,開展蒙特卡羅仿真,生成樣本容量為N的仿真退化數據;統計各樣本失效時間Th,其中h=1,2,…,N;統計t時刻未失效樣本個數N′(t),即滿足Th>t的樣本個數,則t時刻可靠度為R(t)=N′(t)/N。其中,生成仿真數據具體包括以下步驟。 步驟 1設定仿真時間和步長等參數,為了確保仿真樣本在仿真期間發(fā)生失效,仿真時間應盡量長一些。設仿真時間步長為Δt,仿真時刻數為M,則總仿真時長為MΔt。 步驟 2從退化增量聯合分布C(F1(ΔX1j),F2(ΔX2j);θ)生成仿真時間段[(s-1)Δt,sΔt]內指標退化增量[ΔX1(sΔt),ΔX2(sΔt)]T,其中s=1,2,…,M。 步驟 3重復步驟2,得到仿真時長內,各指標仿真退化增量,記為 步驟 4對退化增量求和得到仿真樣本在各仿真時刻指標退化量: 步驟 5重復步驟2~步驟4即可得到樣本容量為N的仿真退化數據。 為了驗證本文方法的有效性,采用該方法針對艙門鎖實例開展分析。將本文模型記為M0,如式(8)所示。為體現本文方法適用性,與如下兩種參考方法進行對比:① 現有僅考慮指標間耦合性的雙指標模型,記為M1,模型具體形式見文獻[21],以說明在雙指標退化中考慮階段性的意義;② 實例數據來源于文獻[29],該文獻針對艙門鎖的退化特點建立了一種分析方法,將文獻[29]方法記為M2。 采用本文模型對艙門鎖性能退化數據進行退化建模和參數估計,得到對數似然函數log-LF(tw1,tw2)隨變點tw1、tw2變化關系如圖2所示。 圖2 log-LF(tw1,tw2)隨變點變化圖Fig.2 log-LF(tw1, tw2) variation with change points tw1 and tw2 表1 本文方法M0參數估計結果 由表1可見,不論對于指標1還是指標2,第一、二階段模型參數都有明顯差異,說明同一指標不同階段退化速率及分散性規(guī)律發(fā)生變化;此外,不同階段Copula參數的不同說明不同階段指標間相關性規(guī)律存在差異。 為了對比各模型擬合效果,表2列出了3種模型的對數似然函數值和AIC(akaike information criterion)值。其中AIC值定義如下: AIC=-2(log-LF)+2n′ (18) 式中:n′為未知模型參數個數。AIC值越小,模型擬合能力更優(yōu)。 表2 log-LF值和AIC值對比結果 由表2可見,本文模型M0的log-LF和AIC值均優(yōu)于參考模型,這是由于本文方法同時考慮產品退化過程中的階段性與相關性規(guī)律,能夠合理描述退化過程。 為了更為直觀說明3種模型擬合效果及參數估計準確性,圖3給出了平均退化曲線對比結果。從圖3中可知,對于指標1和指標2,本文方法M0給出的平均退化曲線能夠有效描述樣本均值的變化規(guī)律。 圖3 平均退化曲線對比結果Fig.3 Comparision results of mean degradation curves 進一步,基于M0、M1和M2對艙門鎖進行可靠性評估。指標1和指標2失效閾值分別為D1=1.6、D2=0.9。圖4展示了基于各模型得到的產品可靠度曲線,可見相較于本文模型M0,僅考慮兩指標耦合性的模型M1前期結果偏保守,后期結果偏危險;模型M2得到的可靠性評估結果最為保守。 圖4 可靠度曲線對比結果Fig.4 Comparative results of reliability curves 通過以上對比說明本實例中,當產品具有雙指標聯合、階段性退化特點時,須綜合考慮兩方面特點進行合理建模,方能開展有效的可靠性分析。 針對產品同時具有雙指標耦合性與階段性退化規(guī)律,本文提出了一種雙指標階段性退化模型,并建立了可靠性分析方法。針對兩指標變點不在同一位置的一般情況,本文建立了一種考慮雙指標變點的模型參數整體估計方法。通過實例分析,驗證本文方法的有效性。結論如下: (1) 雙指標耦合退化且存在階段性規(guī)律時,不同階段指標間的耦合性強弱可能不一致,建立退化模型時應予以考慮; (2) 本文方法能有效表征退化過程中兩指標的耦合性與階段性規(guī)律,可靠性評估結果更為準確可信,符合工程實際需求。
f1(ΔX1j)·f2(ΔX2j)4 實例分析

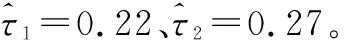



5 結 論

