實時電價下含換電站的孤立微電網雙層優化調度

王 昊，郭興眾，楊秀茹

(安徽工程大學 高端裝備先進感知與智能控制教育部重點實驗室，安徽 蕪湖 241000)

面對全球能源不斷緊張的局面，電動汽車產業已經成為熱門產業。我國近些年加大了對電動汽車產業的投入，電動汽車可以充當負荷吸收微電網中多余的能量，將電動汽車入網技術運用于微電網，可以實現微電網盈利。

伴隨電動汽車進入人們的生活，電動汽車電池換電站作為電動汽車能源供給的主要來源應運而生。將換電站與含可再生能源的微電網結合，對有效利用可再生能源具有重大作用，使得換電站和微電網各自的收益最大。文獻[5-6]分別在充電和換電兩種不同的模式下計算含電動汽車的微電網經濟調度模型，證明了在相同條件下，換電模式比充電模式更能提高微電網的經濟性。文獻[7]在含分布式電源的微電網模型基礎上，加入電動汽車換電站模型，論證了換電站的儲能作用。文獻[8]以網損最小為目標函數，利用遺傳算法對含有光伏發電的充電站集中調度，通過充電站最優充放電計劃的安排降低負荷峰谷差和網損。文獻[9]提出了微電網和電動汽車換電站的模型，利用入侵雜草算法優化，同時對比其他優化算法突出此算法的優越性。文獻[10]建立不同目標函數，以換電站充電功率為變量參與有序充電調度。

目前對微電網的研究多集中于微電網的經濟調度優化問題。文獻[11]從負荷需求側出發，綜合考慮微源出力、需求側管理、環境治理三種成本為目標函數，運用改進粒子群算法優化，最后解決了孤立微電網供電不足的問題。文獻[12]考慮了可再生能源出力不穩定性對孤立微電網的影響，將基礎負荷功率電源和調頻電源作為調頻特性的部分，實施兩步優化，先日前調度確定基礎電源的出力，再制定調頻電源的出力方案。但是，此調度未能發揮基礎電源出力的靈活性，降低了微電網的調節能力。

研究將傳統儲能系統接入微電網的模式代替為電動汽車電池交換站的接入。以風電機組、光伏機組、電動汽車電池交換站及柴油發電機組作為孤立微電網的內部結構模型，以孤立微電網成本最小和換電站利益最大分別建立雙層模型，以不平衡功率引導的電價和換電站充放電總功率作為雙層模型聯系的橋梁，并以此網為例驗證模型的有效性。

1 孤立微電網結構和雙層調度

研究基于換電站的孤立微電網模型。微電網內部由風機、光伏、柴油發電機、電池換電站及負荷組成。其中，風、光是自然資源，不同時刻的出力具有不確定性，輸出功率不可控；柴油發電機屬于可控制的分布式電源，可以由微電網控制其出力。而換電站與微電網不是同一個經濟實體，所以兩者之間的調度須通過微電網制定的電價引導換電站的出力，進而將換電站的出力計劃反饋給微電網，微電網得到反饋優化柴油機的出力，調整電價。

含換電站的孤立微電網調度如圖1所示。由圖1可知，上層模型通過制定內部電價優化下層換電站充、放電功率，下層將功率反饋給上層微電網，從而實現兩者的利益最大化。其中，電價是自變量，換電站的出力功率是因變量。

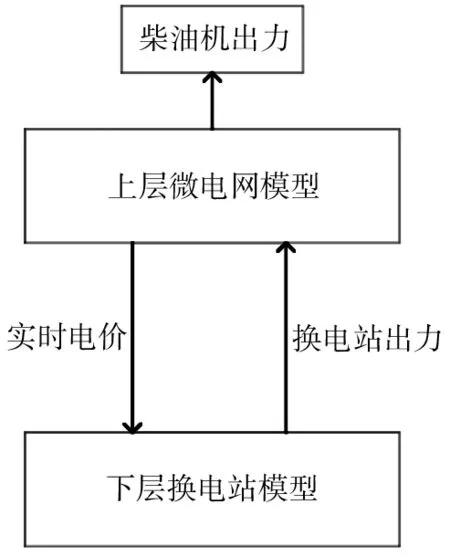
圖1 含換電站的孤立微電網調度

2 基于雙層優化的孤立微電網模型

2.1 上層孤立微電網模型

上層模型是通過優化柴油發電機不同時刻的出力以及制定電價使其凈成本最小。

(1)風機(WT)數學模型。

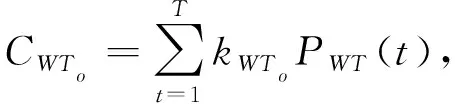
(1)

(2)

C

=

C

+

C

,

(3)

式中，

C

表示WT運行時需要的管理成本；

C

表示WT管理電源產生的費用;

k

表示WT單位運行的維護系數；

k

表示WT發電管理費用系數；

P

(

t

)為第

t

時段WT出力；

T

為調度周期。

(2)光伏發電(PV)模型。

(4)

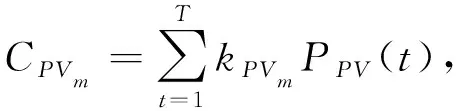
(5)

C

=

C

+

C

,

(6)

式中，

C

表示PV運行時需要的管理成本;

C

表示PV管理電源產生的成本費用;

k

表示PV單位運行時的維護系數；

k

表示PV的發電管理費用系數；

P

(

t

)為第

t

時段PV出力;

T

為調度周期。

(3)柴油發電模型。設定微電網處于孤島運行情景下，故除分布式電源供電以外的微電網剩余負荷均由柴油發電機組承擔。柴油發電機在運行的過程中會產生運行費、燃料費和氣體污染處理費用。

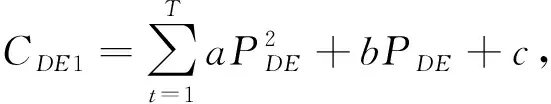
(7)

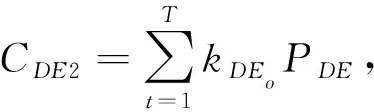
(8)

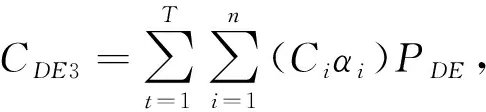
(9)

C

=

C

1+

C

2+

C

3，

(10)

式中，

C

1為柴油機消耗燃料的成本；

C

2為柴油機的運行成本；

C

3為柴油機對氣體污染物的處理成本；

P

為柴油發電機的實際功率；

a

、

b

、

c

分別為柴油發電機的系數；

k

是柴油機的運行維護系數；

C

是對

i

類氣體污染物處理的成本系數;

α

是柴油機運行時產生

i

類氣體污染物的排放量。

(4)可中斷負荷模型。孤立微電網主要用于偏遠的地方，遠離大電網，利用內部微源獨立發電作用于負荷。當微源出力不足以提供負荷供電需求時，則需要考慮中斷負荷的供應，由電網控制負荷的工作狀態，對被中斷負荷的用戶給予補償。

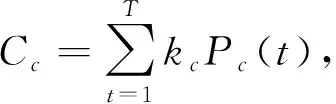
(11)

式中，

C

為孤立微電網出力不足而導致的中斷負荷補償成本；

k

表示中斷負荷的單位補償費用；

P

(

t

)為

t

時刻中斷負荷的功率。

(5)棄風、棄光成本模型。在負荷水平不高的情況下，微電網中會存在多余的微源出力，造成可再生能源的浪費，主要存在多余風、光能源的不及時消納。其成本模型如下：

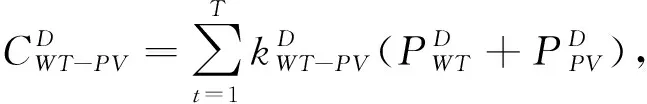
(12)

(6)能量交換成本。換電站在低負荷的階段吸收多余的微電網功率，在高負荷階段釋放自身存儲的功率，起到削峰填谷的作用，所以換電站與微電網之間存在能量交換，成本模型如下：

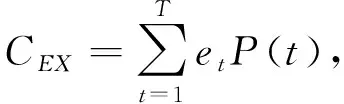
(13)

式中，

C

為能量交換成本;

e

為

t

時刻的電價;

P

(

t

)為微電網和換電站在

t

時刻的交換功率，換電站向微電網購電時

P

(

t

)為正，反之為負。

綜上，孤立微電網的成本模型如下：

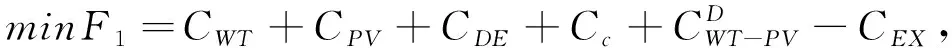
(14)

上層目標函數的約束條件如下：

①功率平衡約束

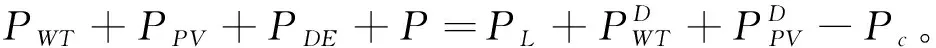
(15)

②柴油發電機功率約束

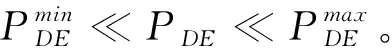
(16)

2.2 下層電動汽車換電站的模型

電動汽車換電站可以更換電動汽車的電池，并對換下的電池進行充放電并存儲。本模型以整個換電站的儲能為控制目標，對其參與微電網的充、放電過程進行控制。在任意

t

時刻，換電站內有一部分電機處于充電狀態，也有一部分電機處于放電狀態，所以在

t

時刻換電站總的充放電功率為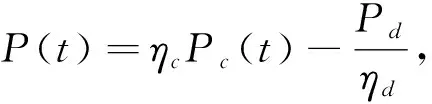

(17)

式中，

P

(

t

)、

P

分別是電機在

t

時刻的總充、放電功率;

η

、

η

分別是充、放電效率。

換電站根據上層的電價調整自身的充放電功率，從而實現換電站利益最大化，即

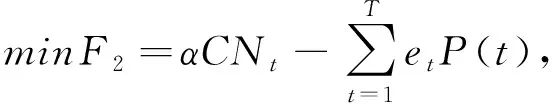
(18)

式中，

α

為換電站向電動汽車用戶提供的換電零售價；

N

是電動汽車用戶向換電站更換電池的需求量；

C

為電池的額定容量。

下層目標函數的約束條件如下:

(1)任何時刻換電站電池電量應該滿足用戶的換電需求

CN

≤

q

≤

q

，

(19)

式中，

q

是換電站

t

時刻存儲的電池電量；

q

是換電站最大存儲電量。

(2)電量平衡

q

=

q

-1+

P

-1

Δt

-

CN

-1。

(20)

(3)換電站內電機的數量有限，所以總充放電功率具有約束。在

t

時刻，換電站最大的充、放電功率為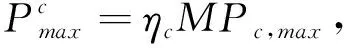

(21)

(22)

(23)

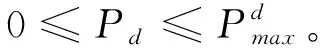
(24)

2.3 實時電價的制定

為了優化換電站充放電功率，孤立微電網采用實時動態電價模式。分時電價具有改善用戶充電習慣，對微電網內部起到削峰填谷，降低微電網和用戶費用成本的作用，是時間段的電價。研究的電價是根據每一個時刻的負荷變化來制定每一時刻的相應電價，是時間點的電價。

實時動態電價是基于不平衡功率來制定的。當微電網孤立運行時，電網中不平衡功率為

P

=

P

+

P

+

P

-

P

,

(25)

為了制定實時動態電價，引入不平衡率

U

，計算如式(26)所示：

(26)

根據以上

U

的值，

U

在各個取值范圍的電價如表1所示。

表1 波動范圍和電價的制定

3 基于改進遺傳算法的雙層模型優化

研究基于改進遺傳算法求解雙層優化模型。為提高最優解和優化效率，研究對傳統遺傳算法加以改進。對于實數問題的優化，設置一個步長為

step

的鄰域擾動算子，將個體的染色體任意一個位置進行一點或多點擾動，即隨機生成-1至1之間的隨機數

rand

，然后在染色體原位置上的值加上

step

*

rand

。引入步長

step

，整體擾動策略分為兩個部分，將全局擾動策略運用于總進化次數的前一半，即將每個染色體的基因位都進行擾動；同理，將局部擾動策略運用于總進化次數的剩余過程，即從個體的染色體中任意選擇一個基因位進行擾動，且擾動的步長為

step

=

step

*(1-

rate

)，

(27)

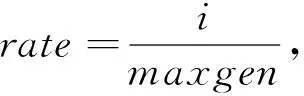
(28)

式中，

rate

是迭代次數；

i

是當前迭代次數；

maxgen

是最大迭代次數，即步長隨著進化代數的增加而降低。擾動變量

r

作如下改進:

low

=-

step

，

(29)

up

=

step

，

(30)

(1)

rate

<0

.

5，

r

=

r

*(

up

-

low

)+

low

。

(31)

(2)

rate

>0

.

5，存在擾動概率

m

，當

rand

<

m

，

r

=

rand

*(

up

-

low

)+

low

,

(32)

式中，

low

、

up

分別是擾動下界和擾動上界；

rand

是0～1的隨機數。最后，把擾動變量的值賦予個體，得到新個體進入下次優化。

采用整體策略的好處在于，不僅使算法前期收斂速度快，而且后期算法的局部搜索能力也大為提高。運用此種改進遺傳算法解決研究雙層模型的具體求解流程如圖2所示。

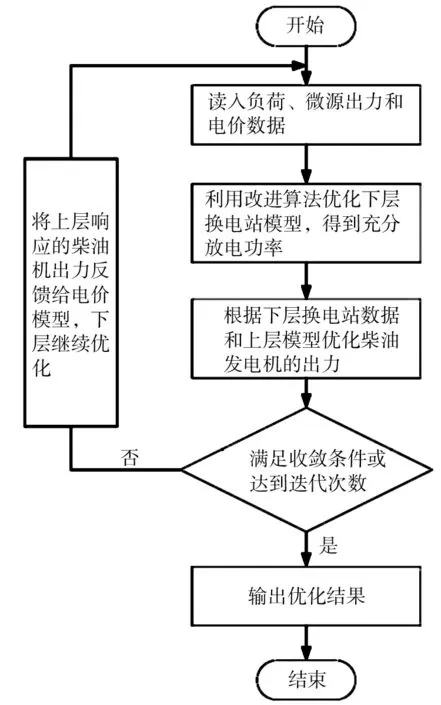
圖2 改進遺傳算法求解模型

4 算例分析

4.1 參數設置

孤立微電網系統由風電機組、光伏機組、電動汽車電池交換站及柴油發電機組成。微電網內部基礎參數如下：柴油發電機的出力限制范圍為0～100 kW,系數a、b、c分別為0.000 11、0.180 1、6。調度周期為1 d，設定1 h為一個研究時段。微電網中基礎負荷功率數據和風光發電出力的預測數據分別如圖3、圖4所示。各微源的成本系數，柴油發電機的污染物排放量和治理費用，以及微電網棄風棄光和切負荷的單位補償成本系數分別如表2、表3、表4所示。

表2 各個微源的成本系數

表3 污染物治理費用和排放系數

表4 棄風棄光和切負荷單位補償成本

圖3 負荷功率曲線圖4 風光出力預測曲線

換電站的參數如下：假定換電站有50臺充放電機，充放電功率均為8 kW，充放電效率均為0.95；站內每個電動汽車的電池容量均為30 kWh，型號均相同。換電零售價取統一價格為1.3 元/(kW·h)。電動汽車各時段的換電需求以及微電網一天的分時電價如圖5、表5所示。

圖5 用戶換電需求

表5 分時電價數據

改進遺傳算法參數為：種群規模為100，交叉概率、變異概率分別為0.6、0.01，最大迭代次數為1 000。步長因子越大，加快收斂，結果容易在最優值附近震蕩;而因子越小，收斂減慢，但容易找到最優值。綜上，步長因子為0.001。

4.2 結果分析

為了說明孤立微電網與電動汽車換電站互動帶來的經濟效益，研究設計了兩種方案進行仿真對比：方案1是基于分時電價下孤立微電網與電動汽車換電站的互動；方案2是基于實時電價下孤立微電網與電動汽車換電站的互動。

方案1及方案2的換電站總充放電功率曲線圖如圖6、圖7所示。上述兩類圖中換電站都滿足在低電價階段大規模充電,在高電價階段適當放電，以此增加換電站收益。但圖7在采用實時電價后，換電站總充放電功率隨每時刻電價的變化而變化，且變化范圍大、頻率高、追蹤效果好。所以方案2下換電站收益更好。

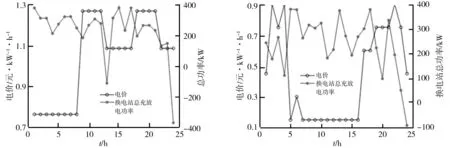
圖6 方案1中換電站總充放電功率圖7 方案2中換電站總充放電功率

兩種方案下微電網總成本和換電站總利潤如表6所示。方案1和方案2中微電網的總成本如圖8、圖9所示。方案1和方案2中換電站的總利潤如圖10、圖11所示。由表6可以看出，在微電網總成本方面，方案1的總成本為4 938.96元，而方案2的總成本為3 374.81元。對比方案1，方案2的微電網總成本減少了1 564.15元，即31.7%；在兩者換電站收益方面，方案1、方案2的換電站收益分別為625.21和3 641.47元，相比方案1可以看出，方案2收益增加明顯，為482%。上述分析表明，實時電價的實行有利于最大化微電網和換電站的經濟利益。

表6 兩種方案中微電網成本和換電站利潤

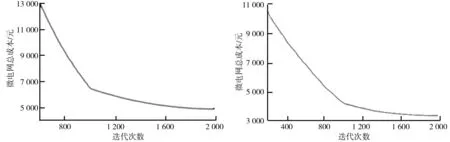
圖8 方案1中微電網總成本圖9 方案2中微電網總成本

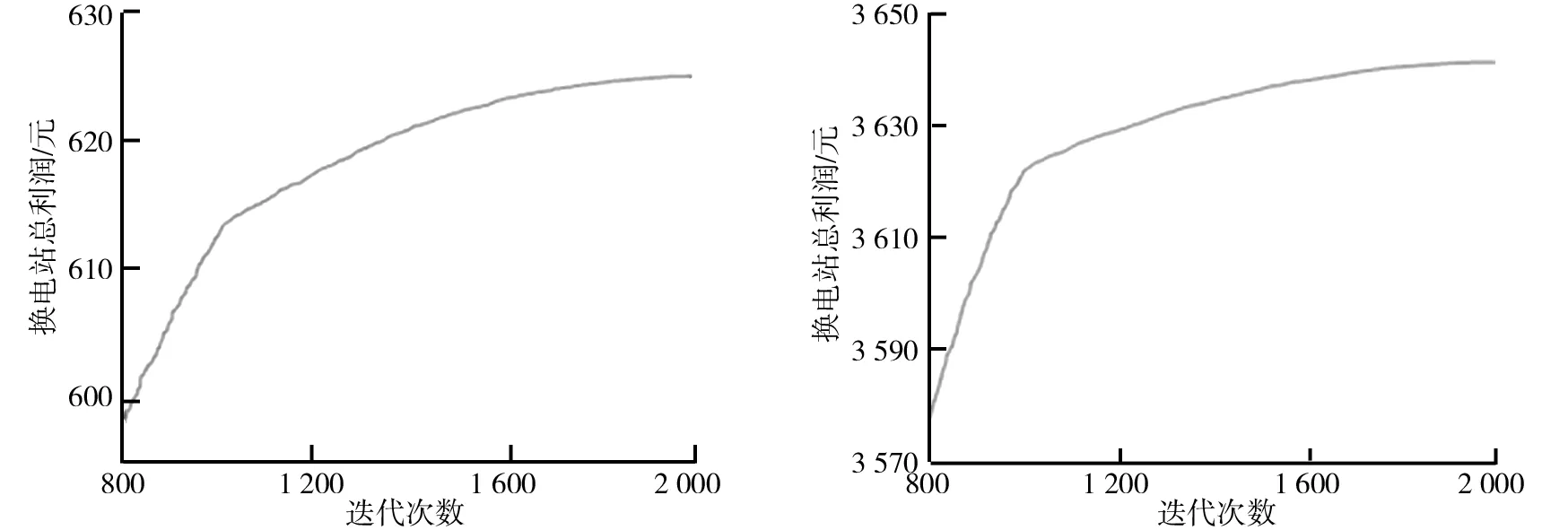
圖10 方案1中換電站總利潤圖11 方案2中換電站總利潤

模擬退火算法學習的是金屬退火的原理，是由開始給定的溫度慢慢冷卻的過程。由于該算法有一定的概率跳出局部最優解，能以較快速度找到問題的近似最優解，但并不一定能找到全局最優解，同時，結果也受到溫度的初始值和退火速度等影響。為了比較改進遺傳算法的優越性，研究用模擬退火算法對微電網和換電站的雙層模型進行優化，對比兩種算法的結果。模擬退火算法下在實時電價方案中微電網的總成本和換電站的總利潤如圖12、圖13所示。對比圖12、圖13，在微電網總成本方面，改進遺傳算法的最優值好于模擬退火算法，其擁有更好的全局搜索最優解的能力。在換電站利潤方面，模擬退火算法收斂速度過快，導致得不到全局最優解。

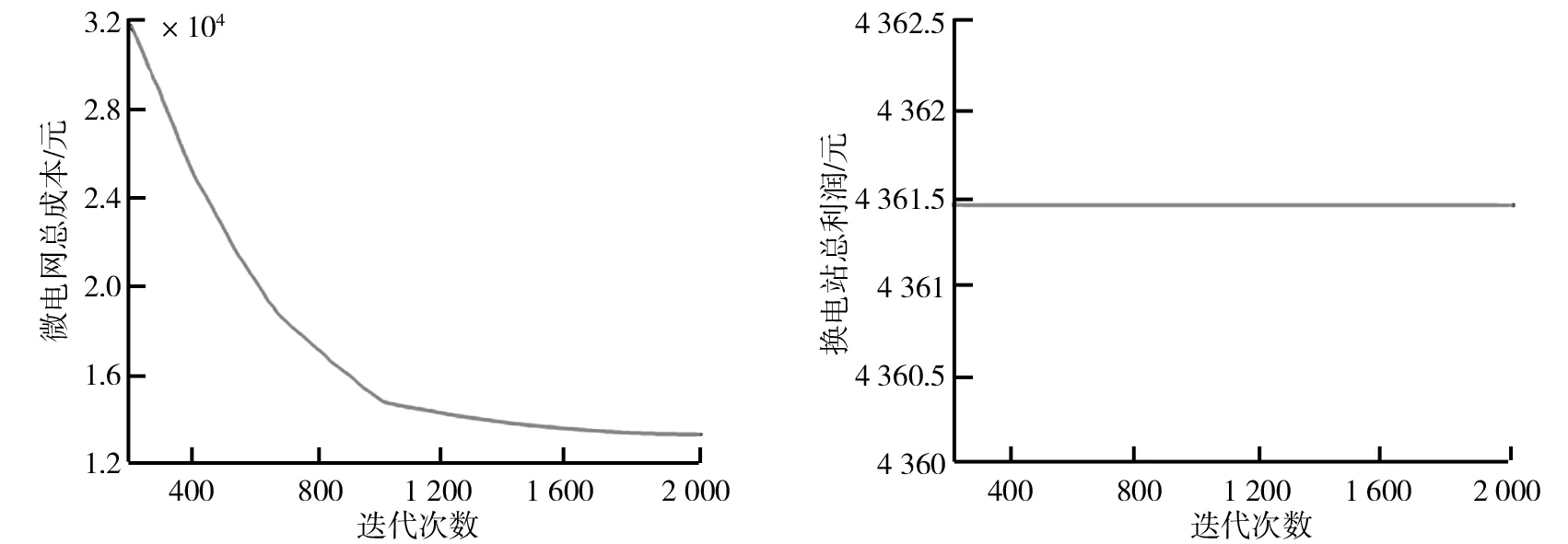
圖12 模擬退火算法下微電網總成本圖13 模擬退火算法下換電站總利潤

5 結論

研究利用改進遺傳算法對孤立微電網和電動汽車電池換電站兩種不同的利益主體的雙層模型進行優化。仿真結果表明，研究提出的基于孤立微電網和電動汽車電池換電站的雙層模型及算法不僅可以降低微電網成本，而且可以最大化換電站的利益。同時，與模擬退火算法相比，改進遺傳算法精度更高。