馬爾科夫鏈驅動的帶停時的超前倒向隨機微分方程的適應解

陳 威，李志民，張雪峰

(安徽工程大學 數(shù)理與金融學院，安徽 蕪湖 241000)

Pardoux等首次提出了倒向隨機微分方程(BSDEs)的概念，其形式如下:

-

dY

=

g

(

t

，

Y

，

Z

)

dt

-

Z

dW

，

t

∈[0，

T

]。

Cohen等在此基礎上考慮馬爾科夫鏈驅動的BSDEs，證明其適應解的存在唯一性。肖新玲等利用連續(xù)性方法研究由馬爾科夫鏈驅動的BSDEs關于初值的比較定理。隨后，肖新玲通過迭代法證明了由馬爾科夫鏈驅動的BSDEs解的存在唯一性。Peng等考慮生成元中包含當前和未來時刻解的情況，給出超前倒向隨機微分方程(超前BSDEs)的概念，其形式如下:

式中，

α

(·):[0，

T

]→

R

與

β

(·):[0，

T

]→

R

是滿足下面條件的連續(xù)函數(shù)：(1)存在某一常數(shù)

K

≥0，使得對任何

t

∈[0，

T

]，

t

+

α

(

t

)≤

T

+

K

，

t

+

β

(

t

)≤

T

+

K

。(2)存在某一常數(shù)

C

≥0，使得對任何

t

∈[0，

T

]以及非負可積函數(shù)

f

(·)，

隨后，楊哲對其理論做出進一步研究。Lu Wen等在以上工作的啟發(fā)下，提出如下形式的由馬爾科夫鏈驅動的超前BSDE：

式中，

α

(·):[0，

T

]→

R

與

β

(·):[0，

T

]→

R

是滿足假設(1)和(2)的連續(xù)函數(shù)。

由于由馬爾科夫鏈驅動的超前BSDEs的生成元包含當前和未來的解,且有限停時在期權定價中有著至關重要的作用，因此，帶有停時的超前BSDEs在金融市場中具有非常廣闊的應用前景。呂思宇研究了馬爾科夫鏈驅動的超前BSDEs在金融中的應用。陳增敬考慮終端條件為有限停時，討論了一類BSDEs在隨機區(qū)間上解的存在性與唯一性。司徒榮等考慮終端條件為無界停時，討論了一類BSDEs在隨機區(qū)間上解的存在性與唯一性。Yang等在超前BSDEs生成元不含Z的超前項這一假設下，討論了一類帶有停時的超前BSDEs解的存在性與唯一性，并得到了一個關于解的逆比較定理。文獻[6]考慮由馬爾科夫鏈驅動的超前BSDEs解的存在唯一性。文獻[11]在固定時間區(qū)間上考慮超前BSDEs生成元中不含Z的超前項。研究在此基礎上引發(fā)一個猜想：生成元中包含Z的超前項的由馬爾科夫鏈驅動的超前BSDEs在有限隨機區(qū)間上是否存在唯一解，答案是肯定的。研究嘗試通過有限隨機區(qū)間上的由馬爾科夫鏈驅動的超前BSDEs來解決這個問題，其生成元中包含Z的超前項。研究證明由馬爾科夫鏈驅動的帶有停時的超前BSDEs存在唯一適應解。

1 預備知識

設

T

∈[0，∞]，

X

={(

X

)≥0}是連續(xù)時間有限狀態(tài)馬爾科夫鏈。馬爾科夫鏈的狀態(tài)空間可以用

R

中的單位向量表示為

S

={

e

，

e

，…，

e

}，其中

N

是馬爾科夫鏈上的狀態(tài)數(shù)。(

Ω

，

F

，

P

)是

T

上的完備概率空間，(

M

)≥0是定義在該空間上與馬爾科夫鏈{(

X

)≥0}有關的平方可積鞅，(

F

)≥0是由(

X

)≥0生成的

σ

域流。對任意的

z

∈

R

，‖

z

‖為歐式范數(shù)。設

Q

為馬爾科夫鏈

X

在時刻

t

的速率矩陣，定義數(shù)量關系如下：

式中，

A

表示

A

的轉置。

定義空間如下：

L

(

Ω

，

F

，

P

)={

ξ

；

ξ

是

R

值，

F

是可測的，

E

[‖

ξ

‖]<∞}。

對任意的

t

∈[0，

T

]，定義

對任意的(

Y

，

Z

)∈

B

，考慮

Y

、

Z

的范數(shù)：

定義(

Y

，

Z

)的范數(shù)：

式中，

B

是一個Banach空間。設有限停時

τ

<+∞，考慮下面由馬爾科夫鏈驅動的帶停時的超前BSDE：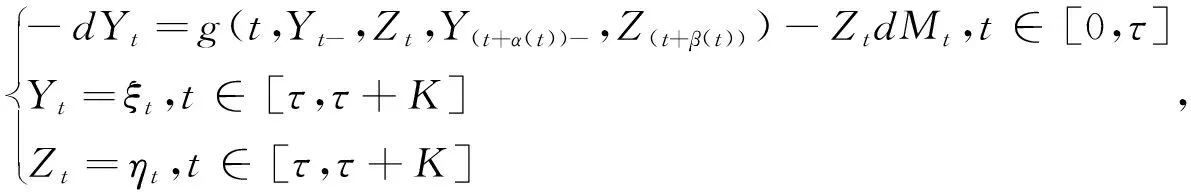

(1)

式中，

α

(·):[0，

τ

]→

R

與

β

(·):[0，

τ

]→

R

是滿足下面條件的連續(xù)函數(shù)：(1)存在某一常數(shù)

K

≥0，使得對任何

t

∈[0，

τ

]，(

t

+

α

(

t

))-≤

τ

+

K

，(

t

+

β

(

t

))-≤

τ

+

K

。(2)存在某一常數(shù)

C

≥0，使得對任何

t

∈[0，

τ

]以及非負可積函數(shù)

f

(·)，

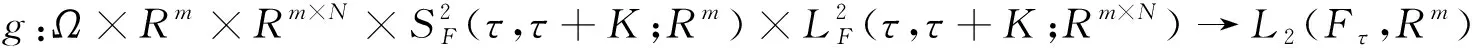
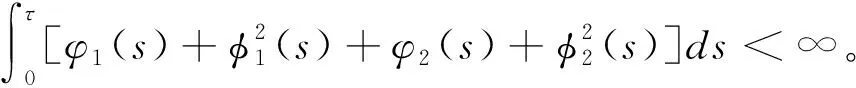
2 解的存在唯一性

考慮由馬爾科夫鏈驅動的帶有停時的超前BSDEs。假設由馬爾科夫鏈驅動的帶停時的超前BSDEs的生成元滿足Lipschitz條件，通過Doob鞅不等式以及不動點定理，證明由馬爾科夫過程驅動的帶有停時的超前BSDEs適應解的存在唯一性。

證明

首先，對給定的常數(shù)

C

，假設

由假設條件(3)可得

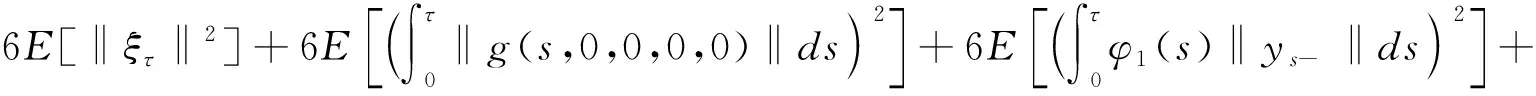
(2)

由Doob鞅不等式可知

E

[

sup

∈[0，](

E

‖

y

(+())-‖)]≤

E

[

sup

∈[0，](

E

(

sup

∈[0，+]‖

y

-‖))]≤4

E

[

sup

∈[0，+]‖

y

-‖]。

(3)

將式(3)代入式(2)可得

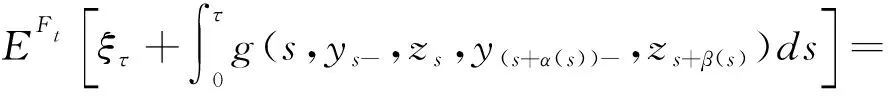
(4)

設

(5)

定義

l

:

B

→

B

是由式(2)、式(3)構造的映射，則

l

:(

y

，

z

)→(

Y

，

Z

)。

(6)

設

(7)

由杜布鞅不等式和假設條件(3)可得

由

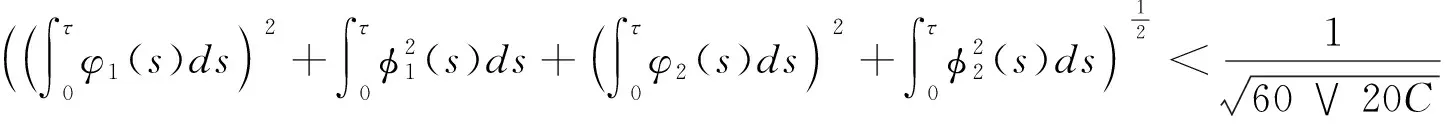
可知

因此，

l

:

B

→

B

是壓縮映射。由不動點定理可知超前BSDE(式(1))存在唯一解。

由假設條件(7)可知

存在常數(shù)

L

使得

設

(8)

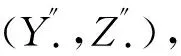
式中，

設

對

t

∈[0，

τ

]，

因此，