大動態干擾下基于光學圖像的自主導航技術

李嘉興,王大軼,鄂薇,葛東明

北京空間飛行器總體設計部,北京 100094

高超聲速飛行器近些年來的發展方向是射程更遠、精度更高[1],這無疑需要更高精度的導航能力。考慮到這種軍事意義十分明顯的飛行器要做到自主導航的迫切需求,探索適合于高超聲速飛行器的自主導航技術成為了目前中國對該領域攻關研究的主要方向之一。天文導航是一種可靠的自主導航方法,在航天領域有很成熟的應用經驗,將其與慣性敏感器進行組合導航可以達到長期穩定且高精度的導航效果。要將天文導航應用于高超聲速飛行器仍處于研究階段,主要受到了氣動光學效應的影響。因為在飛行器高速飛行過程中,星敏感器窗口的大氣被加熱,流場發生巨大改變,產生激波、附面層等復雜流場,光線通過湍流后發生偏折,致使星圖產生偏移、抖動和模糊等負面效果[1],嚴重降低導航能力。為了抑制氣動光學效應,需要首先模擬在高超湍流成像條件下的天文導航圖像,在此基礎上研究圖像復原算法。

目前針對氣動光學效應的研究方法主要包括數值模擬和實驗測量2種方法。數值模擬方法是利用幾何光學、物理光學、統計光學等物理模型,在計算機中模擬光線穿過高速流場后的畸變波前,進而模擬出成像時的點擴散函數。現有的湍流數值模擬方法包括直接模擬法、大渦模擬法和雷諾平均法。直接模擬法能獲得瞬態湍流但計算量巨大；雷諾平均法計算量小但無法模擬出瞬態湍流對光線的影響效果；大渦模擬法計算量居中且能夠表達瞬時流場中的大渦結構,因此本文選用該方法進行氣動光學效應仿真。近些年有不少數值仿真研究,例如Pond和Sutton[2]采用標準k-ε湍流模型對三維凸臺周圍的流場建立了數值仿真,利用相位差、斯特列爾比等參數對氣動光學效應進行了評價。利用大渦模擬法研究氣動光學效應已為主流,White和Visbal[3]對熱壁面和冷壁面可壓縮湍流邊界層引起的航空光學像差進行了大渦模擬,還表明當壁面受熱時光程差會增加。Kamel等[4]驗證了一種帶有壁面模型的大渦模擬方法的有效性。實驗測量方法是直接測量光線穿過真實流場后的光程差數據,研究氣流參數對圖像模糊的影響機理。Gordeyev等[5]通過統計實驗數據獲得了非隔熱壁面上邊界層處波動密度場的預測模型。但這些針對氣動光學效應的研究主要集中于數值仿真模型的建立、流場參數對光學成像指標的影響等方面,很少有面對氣動光學影響下的圖像復原研究。

近些年利用圖像復原技術解決高超聲速飛行器的氣動光學效應問題受到了很高的重視。洪漢玉和張天序[6]在極大似然估計準則的基礎上采用正則化方法復原紅外圖像,文中基于圖像和湍流點擴展函數的梯度變化先驗知識,提出了針對圖像與點擴散函數特點的非線性各向異性正則化函數,使其估計模糊核與清晰圖像時能自適應地平滑梯度。正則化復原方法近些年在國際上也備受關注,學者們利用不同的先驗模型設計正則函數。大多數文獻針對圖像和梯度的分布特點設計模型,Fergus等[7]提出基于變分貝葉斯的圖像盲復原方法,Krishnan和Fergus[8]發現了圖像梯度的重尾分布并用超拉普拉斯分布來擬合。Li等[9]引入了分裂布雷格曼迭代法用于解決非凸優化模型。Ohkoshi等[10]提出結合全變差模型和Shock濾波器的盲復原算法。Zhao等[11]利用Lp范數擬合車牌圖像的分布特征,模糊圖像中同時考慮了離焦與運動模糊問題,并用交替方向乘子(ADMM)算法求解復原模型的最優值。Sun等[12]利用迭代支持檢測方法精細化模糊核,以降低圖像噪聲對模糊核估計結果的精度影響。Pan等[13]提出基于暗通道稀疏先驗知識的盲復原算法。而根據低秩先驗原理,Ma等[14]設計了基于加權核范數正則化和全變差正則化的復原模型,前者能夠降低由相似局部圖像堆疊而成的矩陣的秩,進而約束去噪與模糊復原過程。以上這些圖像模糊復原方法大多是為自然圖像設計,而為了解決氣動光學大動態對天文導航圖像影響,需要針對這種圖像的特點進行專門的復原模型設計,與氣動光學的研究成果相結合。

模糊核的先驗信息有助于獲得更接近真實值的模糊核估計結果[15]。文獻[16]為解決氣動光學效應專門設計了星圖復原算法,利用從圖像中提取的先驗模糊核進行非盲復原。但該方法無法適應先驗模糊核提取精度低或無先驗信息等情況。為了解決這一問題,本文提出一種新的改進算法,在對氣動光學影響下星圖特點研究的基礎上,把先驗模糊核與盲復原方法相結合,設計了新的正則化圖像復原模型,既具備了盲復原算法可以在未知模糊核情形下的復原能力,又具備了非盲復原算法對先驗模糊核中圖像信息的利用能力,提高算法應用時的魯棒性和復原精度。

1 高超湍流場的運動星圖模糊核

基于高超湍流的大渦模擬(LES)流場數據,利用幾何光學和物理光學,湍流場影響下的星圖模糊核,引入隨機運動模糊,建立具有氣動光學效應和運動模糊的高超湍流的運動模糊核。

1.1 高超湍流的大渦模擬

星光經過激波、湍流邊界層、彈體冷卻層等之后,光學窗口外復雜高速流場產生的氣動光學效應使星敏感器接收的圖像存在嚴重的偏移、抖動和模糊。由激波引起的穩定偏折可由文獻[1]中的經驗公式計算,而本文只重點研究湍流模糊與運動模糊問題。

為了盡可能準確地揭示高超湍流場中星光光線傳播的特性,使用大渦模型對湍流流場進行模擬,其流場密度分布如圖1所示。

1.2 湍流影響的星圖模擬

基于上述大渦流場模擬結果,利用物理光學原理,采用光線追擊法,計算平行光穿過流場后的光程差,如圖2所示。根據文獻[1]中的方法,由光程差進一步計算氣動光學效應造成的高超湍流模糊核hH。

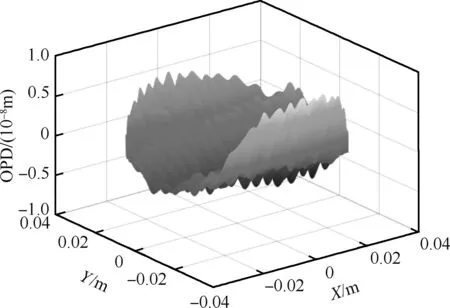
圖2 光程差

當高超聲速飛行器飛行時受到氣流擾動和機體振動導致光軸發生抖動,造成的運動模糊核記為hM,將其與高超湍流模糊核卷積即可得到高超湍流場運動模糊核h,如式(1)所示,卷積結果如圖3所示。

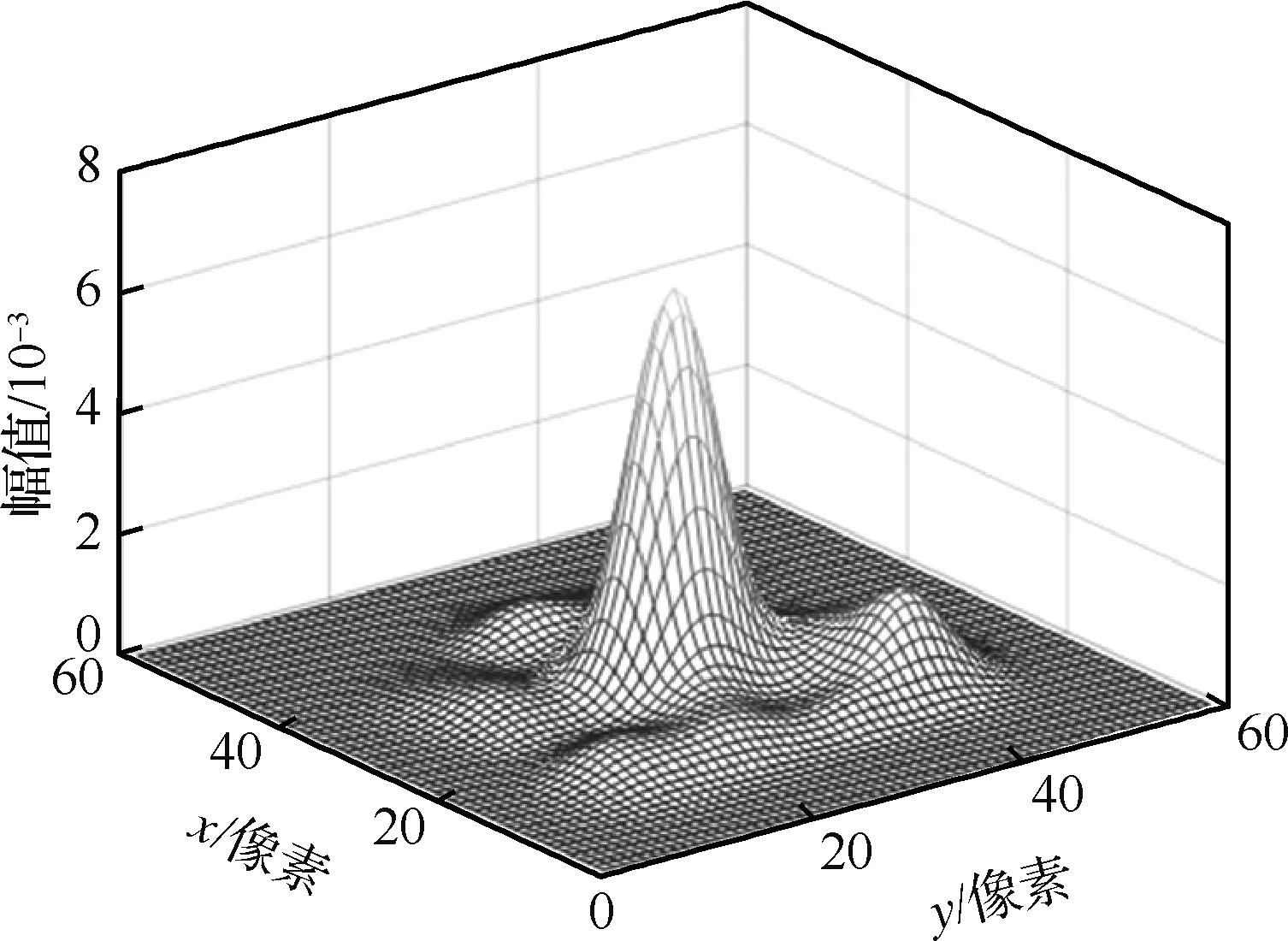
圖3 高超湍流場運動模糊核

h=hH?hM

(1)

式中：?為空間卷積運算,根據湍流凍結理論,在短曝光前提下可將模糊退化過程表示為目標圖像與模糊核的卷積過程,同時考慮噪聲:

g(x,y)=f(x,y)?h(x,y)+n(x,y)

(2)

式中：g(x,y)為退化圖像；f(x,y)為清晰的目標圖像；n(x,y)為加性噪聲。為方便表示,下文將寫作g,f,h,n。

2 先驗模糊核提取與分析

圖像復原是模擬模糊圖像過程的逆過程,在實際導航過程中,需要從模糊圖像當中提取有用信息,利用復原算法獲得清晰圖像。區別于自然圖像當中利用盲復原算法估計模糊核,基于天文導航圖像的獨有特點,可以先從星圖當中提取模糊核的先驗信息來指導復原過程,稱之為先驗模糊核。

2.1 先驗模糊核提取

天文圖像的模糊核提取與光學系統點擴散函數測量問題中的點脈沖法十分相近,星圖中每顆星的圖像與模糊核非常相近,借助這一特性從模糊星圖中提取模糊核的先驗信息,為復原提供依據。但在氣動光學作用下,需解決模糊核重疊、圖像邊界處不完整及成像噪聲等問題。

假設星圖中有M顆星,第m顆星的坐標是(xm,ym),(m=1,2,…,M),能量為Im的星點圖像為Imδ(x-xm,y-ym),其中δ(x,y)為脈沖函數,則原始星圖可表示為

(3)

經過點擴散函數h的退化,并加入噪聲后的退化圖像可表示為

xm,y-ym)+G(μn,σn)

(4)

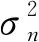
假設1閾值分割階段可以估計出準確的噪聲均值。

當假設1成立時,在退化圖像中去除噪聲均值,即g-μn后,邊界延拓L/2個像素,以(xm,ym)為中心,提取L×L的圖像為

Ωm(x,y)=Imh(x,y)+G(0,σn)+

(5)

式中：L為估計模糊核的支持域邊長,單位為像素個數；Δxmm′=xm′-xm；Δymm′=ym′-ym；D(sm,sm′)為m星到m′星之間的距離。

由式(5)知,Ωm(x,y)中包含m星對應的點擴散函數h、零均值噪聲以及重疊的其他星的干擾能量,將Ωm(x,y)寫為極坐標形式Ωm(r,φ),按照文獻[16]中的算法提取出先驗模糊核。

假設 2利用文獻[16]的算法成功剔除了m星與其他星的模糊重疊區域。

加權融合后的模糊核表示為

(6)

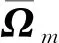
(7)

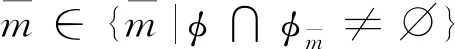
(8)

利用文獻[16]中的先驗模糊核提取算法,能夠剔除相鄰星之間圖像的重疊區域,從而避免了大擾動條件下模糊核重疊的問題。對圖像進行邊界延拓可以使圖像邊界處模糊核不完整時也能正常提取有用信息。

2.2 先驗模糊核特性分析

式(5)在滿足假設2的條件下,可改寫為

(9)

期望和方差為

(10)

(11)

將式(7)、式(9)代入式(6)可得

(12)

則期望和方差為

E(hp(r,φ))=h(r,φ)

(13)

(14)

在滿足假設1和假設2的條件下,式(13)表明模糊核先驗估計hp是退化真實模糊核h的無偏估計。且由式(14)可以看出融合后的hp方差一定不會大于融合之前,而且所利用的圖像信息越多、能量越豐富,方差越小,去噪效果越強。下面定性描述hp與h的差異,為用于表征先驗模糊核的可信任度。

由式(14)得到hp每點處的方差為

(15)

為描述hp與h的誤差,采用二者差值的均方誤差

(16)

將式(15)代入式(16)可得

(17)

同時,均方誤差亦可表示為

(18)

(19)

將式(19)代入式(18)可得

(20)

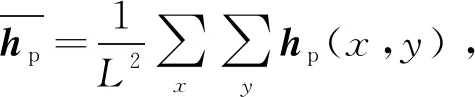
(21)

hp-h為融合后的噪聲,與h相獨立,則

(22)

式中:

(23)

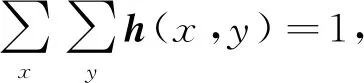
(24)

(25)

將式(17)、式(25)代入式(20)可得hp與h相似度的估計為

(26)

在估計相似度時,只需要先驗模糊核hp和噪聲方差估計值這些已知量,不需要實際模糊核h。因此式(26)的估計方法適用于在未知h的前提下盲復原模糊星圖時,衡量所提取的先驗模糊核的可信任程度,為復原算法在利用hp時提供參數設計依據。

3 高超星圖正則化半盲復原

3.1 半盲復原模型設計

由式(2)所示的圖像退化模型可知,圖像盲復原的過程用數學可以表示成為求解未知量f與h使得后驗概率P(f,h|g)取得最大值,即可表示為如下最大后驗概率問題:

(27)

式中:f*表示清晰圖像的最優估計;h*表示模糊核的最優估計。根據貝葉斯定理,后驗概率P(f,h|g)可以轉化為

(28)

由于在圖像復原過程中模糊圖像g為已知量,因此式(28)中的分母是一個固定的歸一化常數,可以忽略,于是可以得到

P(f|g,h)∝P(g|f,h)P(f)P(h)

(29)

將式(29)代入式(27)可得

(30)

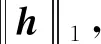
(31)

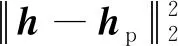
綜上,本章提出的高超星圖正則化半盲復原模型設計為

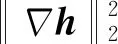
(32)

3.2 最優化求解

為了使模糊核估計更精確,總體求解思路采用文獻[7]中提出的多尺度框架策略,從分辨率由低到高進行逐層復原,特別針對嚴重模糊的圖像,能夠有效避免陷入局部最優。式(32)是一個非凸優化問題,需要交替迭代g與f進行更新。下面為該算法的具體過程,記為算法 1。

3.2.1 目標圖像估計

在更新目標圖像f的階段,固定上一次迭代得到的h,則f的子問題可轉化為如下最優化問題:

(33)

式中：Hf=h?f。

式(33)為Lp范數的優化問題,采用半二次懲罰技術,引入輔助變量a=f,b1=δx?f,b2=δy?f,得到新的目標函數為

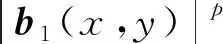
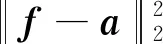
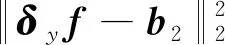
(34)

交替計算f與輔助變量。式中：δx和δy分別表示水平和垂直一階差分算子,δx?f和δy?f簡寫為δxf和δyf。懲罰參數α越大時式(34)的解越接近式(33)的解,最終f可由式(35)計算:

(35)

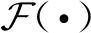
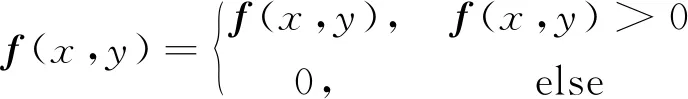
(36)

同時,輔助變量的子問題表示為

(37)

式中：w∈{a,b1,b2}；v∈{f,δxf,δyf}。采用文獻[8]給出的LUT(Look up Table)算法快速求解。

3.2.2 模糊核估計

在更新模糊核h的階段,固定上一次迭代得到的f,則h的子問題可轉化為如下最優化問題:

(38)

式中：Fh=f?h。

式(38)為L1范數的優化問題,利用分裂Bregman迭代來求解。采用半二次懲罰技術,引入輔助變量c=h,式(38)可改寫為迭代框架

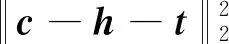
(39)

t:=t+h-c

(40)

固定c、t,更新h的方法為

(41)

利用式(41)更新模糊核后對其進行歸一化

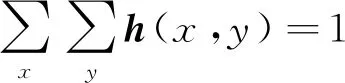
(42)

并為了提高抗噪魯棒性,施加動態閾值約束

(43)

式中：δh表示閾值參數。固定h、t,利用快速收縮算法求解c的最優解:

(44)

綜上,利用算法 1復原圖像的過程如圖4所示。先利用經預處理后的模糊圖像進行目標圖像估計,再利用先驗模糊核和相似度進行模糊核估計,這一過程作為一個循環。每次循環結束前將參數α擴大αInc倍,但不超過αMax,一共進行N次循環。再將算法 1代入文獻[17]中的金字塔算法,來提高大尺度模糊時算法的魯棒性。

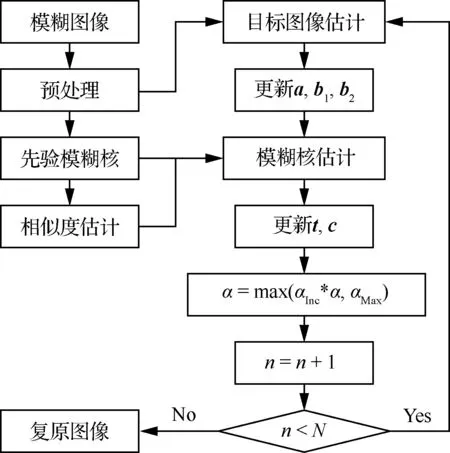
圖4 算法1流程圖

4 算法收斂性驗證

改進的半盲復原算法中,目標圖像估計階段,hp給定,f的子問題為凸優化,其他參數均由查表法獲得最優值,收斂性不必證明。因此只有計算h時的L1約束項通過Bregman分裂法進行近似,因此下文將證明其收斂性。式(38)的遞推式可寫為

(45)

式(45)為L1范數的優化問題,利用分裂Bregman迭代來求解。采用半二次懲罰技術,引入輔助變量c=h,式(45)轉化為無約束分裂形式

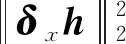
(46)

式(46)可改寫為迭代框架

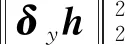
(47)

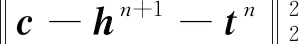
(48)

tn+1=tn+(hn+1-cn+1)

(49)

式(47)～式(49)子問題是凸性可微分的,可得一階最優條件為

0=FT(Fhn+1-g)+θη1hn+1-θη1hp+

(50)

0=rn+1+2β(cn+1-hn+1-tn)

(51)

tn+1=tn+(hn+1-cn+1)

(52)

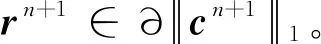
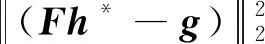
(53)

(54)

并且此解是唯一解。

證明：因為式(46)存在至少一個解h*,其一階最優條件滿足:

(55)

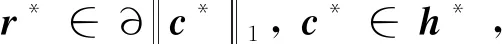
0=FT(Fh*-g)+θη1h*-θη1hp+β(1-θ)×

(56)

0=r*+2β(c*-h*-t*)

(57)

t*=t*+(h*-c*)

(58)

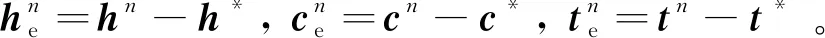
(59)

(60)

(61)

(62)

將式(61)與式(62)相加,得到

(63)

用式(52)減去式(58),可得到

(64)

對式(64)的等號兩邊求平方,得到

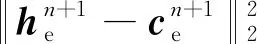
(65)

(66)

將式(66)代入式(63)中,得到

(67)

(68)

(69)

(70)

對式(70)的等號兩邊分別從0到N進行求和運算,可以得到

(71)

式(71)中的各個項都是非負性的,于是有

(72)

假設β,η1,η2,η3>0, 0<θ<1,并且使得N趨近于無窮,對于不等式(72)得到結論

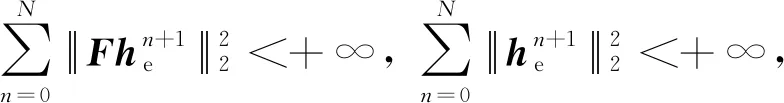
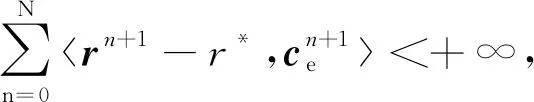
因此可以得到

(73)

(74)

(75)

(76)

(77)

(78)

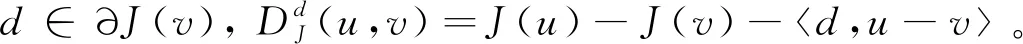
(79)

(80)

hn-h*=0

(81)

(82)

hn-h*=0

(83)

(84)

(85)

綜合式(80)～式(85),可得

(86)

由式(55),可得

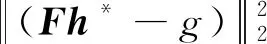
(87)

再結合式(82),即可證明收斂至h*,下面證明解得唯一性：定義

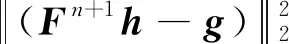
(88)

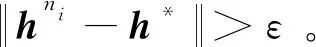
E(hni)>ζE(h*)+(1-ζ)E(hni)≥E(ζh*+

(1-ζ)hni)=E(v)≥min{E(h):

(89)

(90)

存在矛盾,因此h*是唯一最優解。

5 仿真驗證

5.1 仿真條件

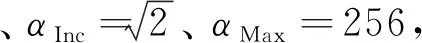
5.2 仿真結果

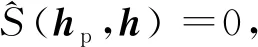
表1 不同算法的平均PSNR對比

從圖5、圖6中可以直觀地得到以下對比結果。CLSF是一種非盲復原算法,因此直接使用先驗模糊核做復原,但這種方法對模糊核估計準確度的要求較高,當模糊核不夠準確時復原圖像精度較低,沒有先驗模糊核時更無法進行復原。Krishna等[18]的算法使用L1先驗,對模糊核和圖像的平滑度略高,可以抑制絕大多數噪聲,但模糊核的形狀比較窄,同時復原的星點較粗,能量不夠集中,出現了相鄰星互相重疊的現象,有時難以區分。Pan和Su[19]的算法使用L0先驗,對圖像表征的稀疏程度更高,雖然復原的圖像能量更集中,但過度保留了圖像和模糊核中梯度的分布,使復原圖像和模糊核中依然存在大量高頻噪聲,可能會對星圖識別造成干擾。文獻[16]是采用了Lp先驗模型的非盲復原方法,平滑程度介于L1和L0之間,在抑制噪聲的同時也使得目標星點能量更集中。相比文獻[16]直接使用先驗模糊核進行復原,算法 2加入了模糊核估計項,是一個盲復原方法,由于其僅依靠傳統的模糊核估計項,得到的模糊核精度依然不高,但同樣采用了Lp先驗模型使得其復原效果低于文獻[16]又強于文獻[18-19]。在先驗模糊核的幫助下,算法 1估計出的模糊核與實際模糊核相差不多,并且由于其具備盲復原的功能,不完全依賴先驗模糊核,能夠在復原過程中對模糊核進行調整,因此其復原效果更佳。

圖5 不同算法的模糊核對比

圖6 不同算法的復原星圖對比

星圖復原后提取質心坐標,與真實坐標進行對比,若二者相差小于2個像素就認為提取正確,并統計正確識別的個數占總個數的識別正確率,如表2所示。造成提取失敗的因素可能有復原后噪聲被放大,被錯誤的提取出來；模糊程度較大的星沒有正確復原,沒有被提取出來；復原后的質心比原始質心偏移較大；兩顆相鄰的星模糊后重疊在一起,復原時沒有將二者分離開等等。將正確識別的星點坐標與真實坐標進行對比,統計二者的平均誤差角距如表2所示。從表中的數據分析算法的復原能力,可以得到與前文相似的結論。同時發現文獻[18-19]和算法 2等盲復原方法質心提取偏差較大的現象,是因為在缺乏先驗模糊核輔助時估計的模糊核不夠準確,沒有擬合出模糊核中的多峰結構,致使復原出來的星點圖像依然存在多峰結構,除主峰以外的次峰會嚴重影響星點質心的計算精度。

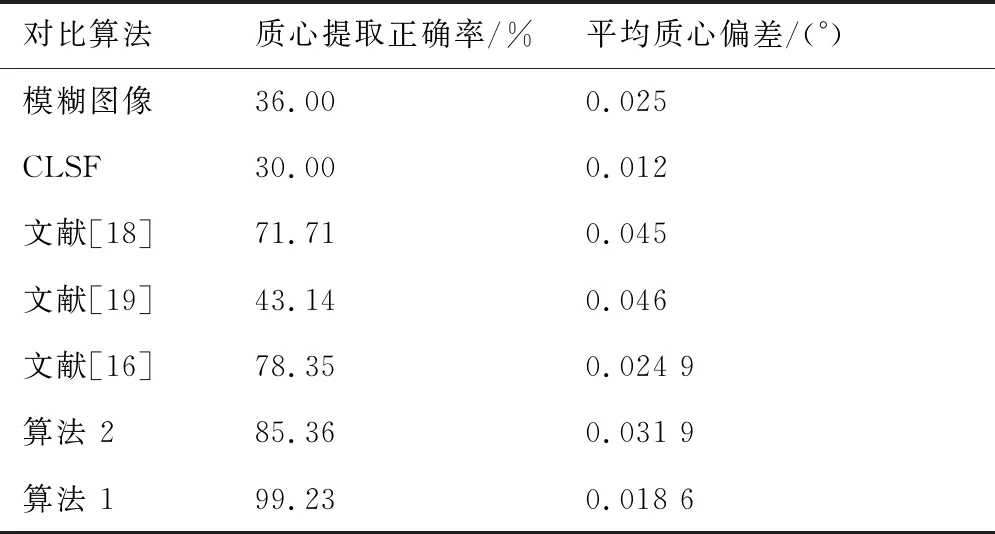
表2 不同算法的質心提取精度對比

采用文獻[20]給出的誤差率作為評價模糊核的估計準確度,對不同算法統計積累誤差率繪制曲線如圖7所示,圖中曲線越高說明模糊核估計得越準確。從圖中可以看出算法 1的模糊核估計準確度更高。

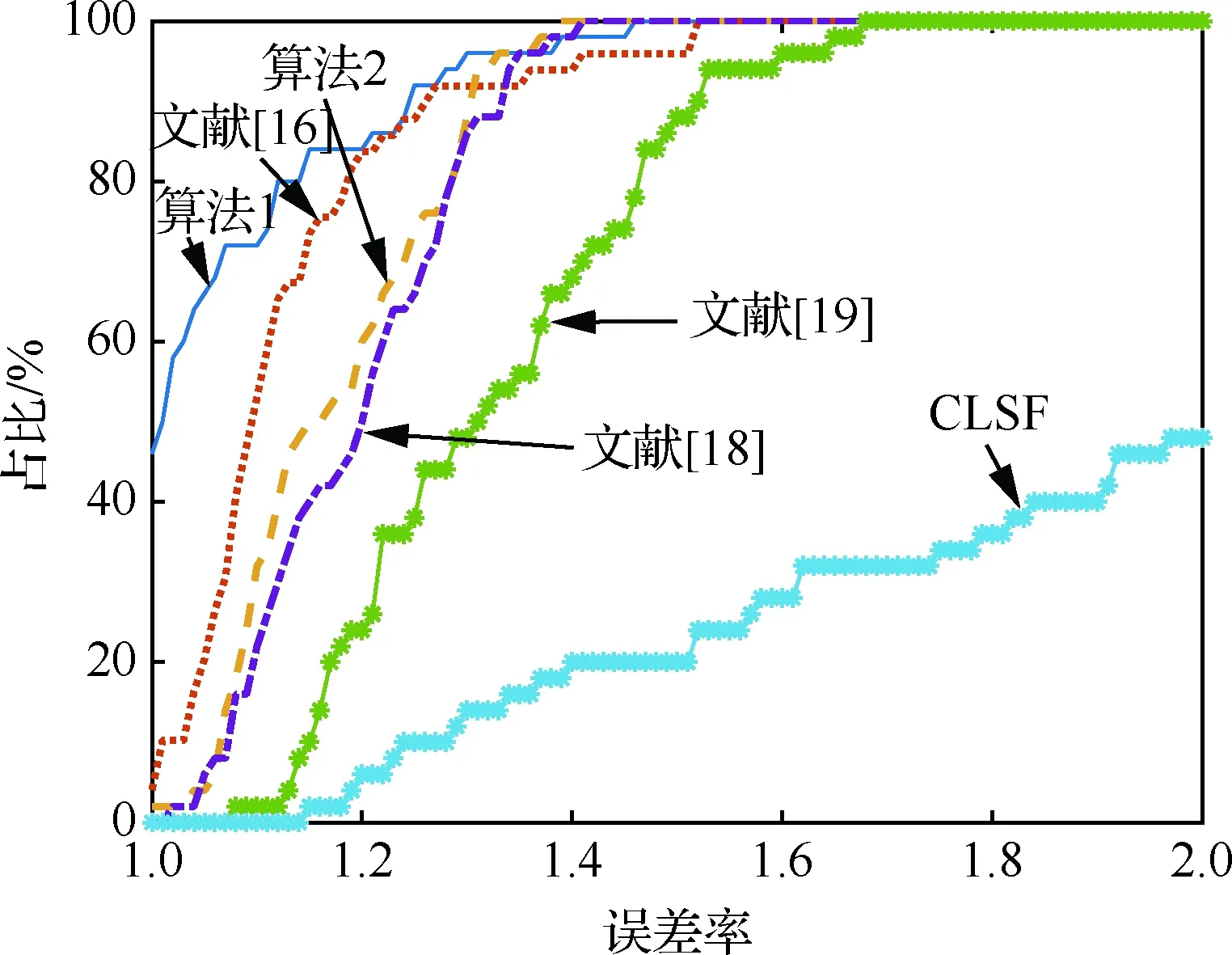
圖7 不同方法的積累誤差率

在6馬赫的飛行速度下,改變飛行高度,利用算法 1復原后的質心偏移曲線如圖8所示,可以看出隨著飛行高度的提升,大氣密度隨指數降低,高超湍流帶來的模糊強度也逐漸降低,因此對質心偏移的影響也逐漸變小。可以看出若想降低氣動光學效應對天文導航精度的影響,除了圖像復原之外,還可以提升飛行高度。

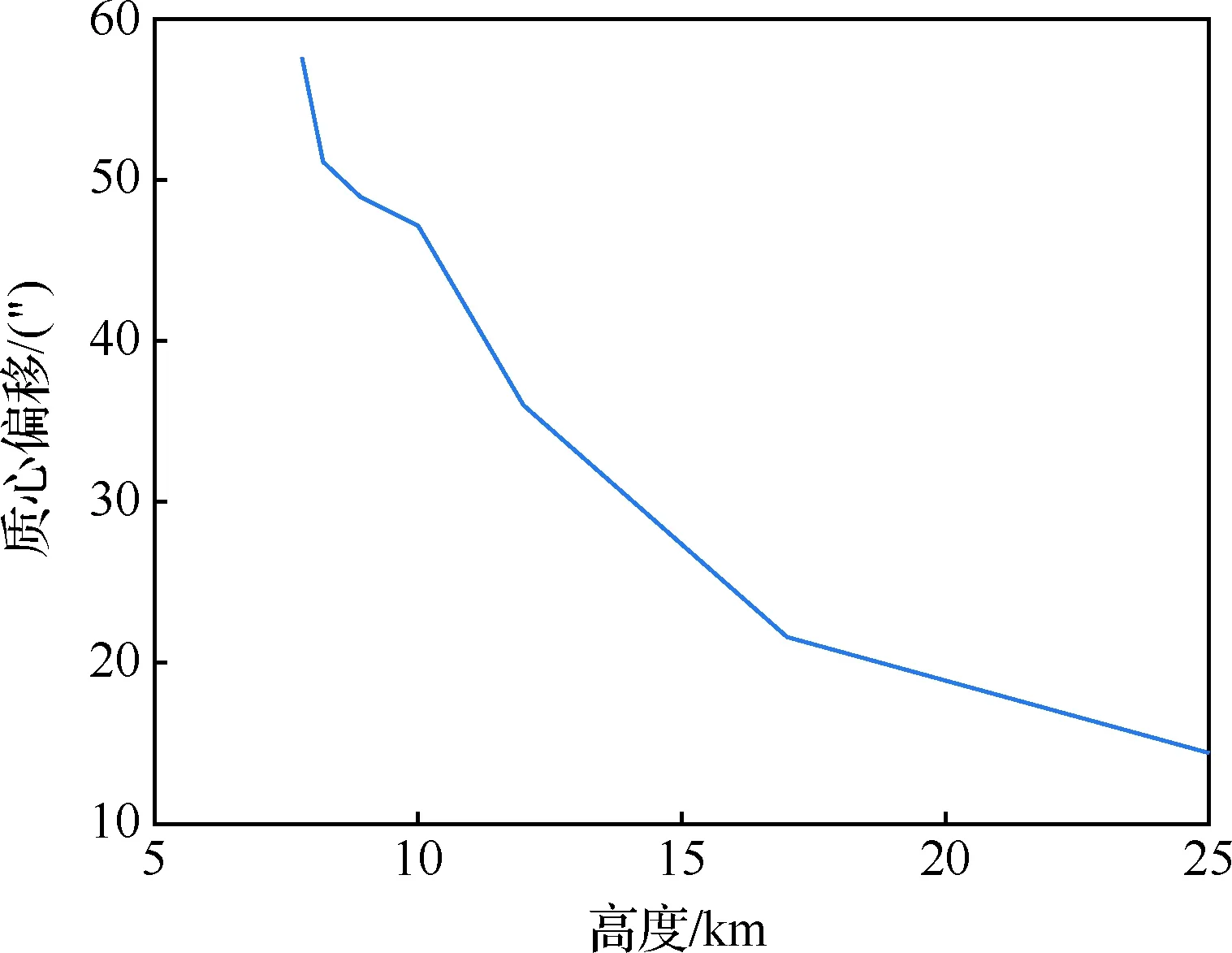
圖8 質心偏移隨飛行高度變化

綜合上述對比分析,本文提出的半盲復原算法相較于其他對比算法,對模糊核的估計更加準確,針對高超湍流模糊星圖的復原效果更好,用于星點質心提取的正確率和精度更高。本文的兩種算法相互對比,帶有模糊核先驗項的算法 1比算法 2效果更好,說明在先驗模糊核的作用之下,估計出的模糊核準確度比完全盲復原時要更高,從而使得復原精度也更高。

6 結 論

針對高超聲速飛行器在平流層中使用天文導航進行自主導航過程中,星圖受氣動光學效應及運動模糊干擾的關鍵問題,深入研究了高超星圖的復原方法,抑制氣動光學效應給天文導航帶來的負面影響。

1) 本文在盲復原算法的基礎上,利用先驗模糊核提供的信息引導模糊核估計的過程,形成了半盲復原模型。

2) 設計了針對復原模型的優化求解算法,交替估計模糊核與清晰圖像,并驗證了該方法的可收斂性。

3) 通過實驗發現提高了模糊核估計的精度,以及復原圖像的精度,最終平均PSNR可達到36.97,質心提取正確率達到99.23%,質心偏差縮小至0.018 6°。

因此該算法可進一步提高高超聲速飛行器的天文導航精度,提升大動態下光學自主導航能力。