基于頻譜不對稱性的雷達輻射源個體識別*

劉魯濤，安賽龍

（1.哈爾濱工程大學信息與通信工程學院，黑龍江 哈爾濱150001；2.哈爾濱工程大學先進船舶通信與信息技術工業(yè)和信息化部重點實驗室，黑龍江哈爾濱150001）

0 引言

隨著電子信息技術的迅猛發(fā)展，電子戰(zhàn)技術的廣泛使用已經成為現(xiàn)代戰(zhàn)爭的主流，敵對雙方在電子戰(zhàn)中的綜合實力將會影響戰(zhàn)爭的走勢。輻射源個體識別是電子支援措施和電子情報系統(tǒng)最困難的任務之一，試圖通過分析截獲的雷達信號來識別單個雷達輻射源，從而確定敵方雷達的位置、性能和技術水平等相關信息。因此，在復雜多變的電磁環(huán)境下精準識別敵方的雷達輻射源具有重要的軍事意義[1]。

傳統(tǒng)的輻射源個體識別方法主要通過提取雷達信號的脈沖描述字參數(shù)特征來實現(xiàn)，如到達時間、到達方向、脈沖寬度、脈沖重復間隔等。隨著電子信息技術的發(fā)展，基于脈沖描述字的參數(shù)特征已無法滿足雷達輻射源個體識別的需求，為了識別復雜電磁環(huán)境下的雷達輻射源，需要分析每個脈沖的內部結構，稱為脈沖的無意調制。脈內無意調制是由于雷達輻射源內部的電子元器件的細微差別而造成的寄生調制，這種無意調制普遍存在并且很難徹底消除[2]。

目前，根據(jù)特征的性質，把提取的特征主要分為時域特征、頻域特征和變換域特征[3]。時域特征包括瞬時幅度、瞬時相位、瞬時頻率[4]等，頻域特征包括雙譜[5]、短時傅里葉變換[6]等，變換域特征包括模糊函數(shù)[7]、變 分 模 態(tài)分解[8-9]、小波包變換[10]、分形方法等[11]。時域特征容易受到噪聲的影響，變換域特征需要進行復雜的變換，本文利用頻譜的不對稱性來進行個體識別，提出基于頻譜不對稱性的輻射源個體識別算法，并利用實測信號對該算法進行了仿真驗證。

1 信號無意調制建模

線性調頻信號(LFM)是一種常見的雷達調制信號，信號表達式如下：

式中，f c是載波頻率，k=B T是調頻斜率，B是頻率變化范圍，T是一個脈沖的寬度。

無意調制會引起頻率漂移、脈沖包絡的改變和相位噪聲[12]。其中，脈沖包絡的改變和頻率漂移對信號的影響較小，相位噪聲對信號的影響是最大的，對于理想的LFM信號，加入相位噪聲后形式變?yōu)椋?/p>

式中,φ(t)為相位上的無意調制，定義無意調制相位噪聲模型為：φ(t)=αsin2πf m t，則LFM信號表達式U(t)可以改寫為：

相位噪聲是由無限個隨機信號調制的綜合結果，所以最終可表示為：

從無意調制模型中可以看出相位噪聲將在f c±f m+1 2k t處隨機產生多個邊帶，并且會在中心頻率兩側產生不同的邊帶，這將會造成頻譜的不對稱。因無意調制具有唯一性，即每個輻射源的無意調制特征都是獨一無二的[13]，所以提取頻譜的不對稱性水平就可以實現(xiàn)輻射源的個體識別。

2 頻譜不對稱性評估

2.1 分數(shù)階傅里葉變換估計LFM參數(shù)

中心頻率的精確定位是評估頻譜不對稱性的關鍵，鑒于分數(shù)階傅里葉變換(FRFT)非常適合處理Chirp這種非平穩(wěn)信號，故采用FRFT方法來估計LFM信號的參數(shù)。

定義在時間域上的線性調頻信號U(t)，其p階FRFT表示為：

式中，K p(t,u)=Aαexp(jπ(u2cotα-2utcscα+t2cotα))是FRFT的核函數(shù)，F(xiàn)RFT的階數(shù)為p，旋轉角度為α=pπ/2。

隨著旋轉角度的不同，信號在分數(shù)階域的能量聚集性也會隨之改變。只有在最優(yōu)旋轉分量時，信號在分數(shù)階域的能量聚集性是最強的[14]，此時，F(xiàn)RFT的結果為沖激函數(shù)δ(f0-ucscα)。圖1為在不同的旋轉角度時分數(shù)階域的結果示意。

圖1 分數(shù)階變換角度旋轉示意

對LFM信號做FRFT，把階數(shù)p當做檢測所用變量，以Δp為搜索步長，在p∈[0,2]范圍內計算不同階次下的FRFT，得到信號在(p,u)平面中的能量分布，在整個時頻域中進行二維搜索，找到能量峰值點所對應的(p0,u0)。利用最佳階次計算出最佳旋轉角度α0=p0π/2，然后就可以對LFM信號的調頻斜率μ0和中心頻率f0參數(shù)進行估計[15]。

根據(jù)調頻斜率、采樣點數(shù)N和采樣頻率f s估計出帶寬B0。

2.2 改進的FRFT算法

當需要較高的參數(shù)估計精度時，需要減小步長Δp，但同時也會使計算量成倍增加。當搜索步長Δp=0.000 01時，可以滿足精度要求，但需要計算200 001次，計算量很大。為了減小計算量，采用多次粗估計來確定最佳階次所在區(qū)間，最后采用一次精估計來確定最佳階次。

根據(jù)文獻[14]可知，信號分數(shù)階頻譜4階原點矩更適合低信噪比下最優(yōu)階次的快速估計，因此利用分數(shù)階頻譜的4階原點矩來估計最佳階次。首先令步長Δp=0.1，在p∈[0,2]的區(qū)間內計算分數(shù)階頻譜的4階原點矩，選出當4階原點矩最大時對應的階次p0，然后更改區(qū)間令p∈[p0-Δp,p0+Δp]。確定區(qū)間后重新進行一次粗估計，更改步長令Δp=0.1Δp，計算出此時4階原點矩最大時對應的階次，更新最優(yōu)階次p0。當進行4次粗估計后更新區(qū)間p，更改步長為Δp=0.000 01，在新的區(qū)間內進行精估計，此時求得的最優(yōu)階次p0就可以用來估計LFM的參數(shù)。改進后的FRFT只需要計算105次，大大減小了計算量，改進算法流程圖如圖2所示。

圖2 改進算法流程圖

2.3 頻譜不對稱性評估

要估計頻譜的不對稱性，需要把時域信號x(t)轉換到頻域X[k]。首先把時域信號進行預處理，去除時域信號的均值，然后進行歸一化處理。為了避免原始信號中突變點或野值點帶來的影響，本文通過取脈沖包絡頂部的多個點，計算得到平均幅值，并除以平均幅值進行歸一化。

運用改進后的FRFT算法對歸一化后的時域信號進行參數(shù)估計，估計出LFM信號的中心頻率f0和帶寬B0。然后采用N點快速傅里葉變換算法(FFT)計算出時域信號的頻譜X[k],k=1,2,…,N-1，并將頻譜歸一化。

公式(9)中的f l i p{·}表示向量的翻轉，τ是對中心頻率校準，在-2≤τ≤2的情況下使X l和X r的歐式距離最小。

把?代入到公式(10)中計算出校準后的X l和X r。

在計算出左右頻譜后，通過能量差、歐幾里得距離和相關系數(shù)來評估頻譜的不對稱性。因相位噪聲的影響，在左右頻譜中隨機產生的多個邊帶是不同的，這將會造成左右頻譜的能量存在差別，故可以以左右頻譜的能量差作為特征進行識別。

歐幾里得距離，又稱歐式距離，是一種用來度量相似度的算法，歐式距離越小，相似度就越大，歐式距離越大，相似度就越小。

相關系數(shù)也可以用來衡量X l和X r的相似度，定義為：

公式(13)中Cov(·)表示計算協(xié)方差，Var(·)計算方差。ρ的取值范圍為[-1,1]，相關系數(shù)|ρ|越接近0，表示相關性越小，|ρ|越接近1，表示相關性越大。

把計算得到的能量差、歐式距離和相關系數(shù)特征組成聯(lián)合特征向量來進行雷達輻射源的個體識別。

3 支持向量機(SVM)分類器

支持向量機是在統(tǒng)計學習理論的基礎上并根據(jù)結構風險最小化的原則提出的一種新的機器學習方法[16]。根據(jù)決策平面原理，找到一個用來分割不同類型數(shù)據(jù)的決策平面，各類數(shù)據(jù)到此決策平面的距離之和越大，分類的可信度也就越大，因此，支持向量機的關鍵問題是找到距離各類數(shù)據(jù)距離之和最大的決策平面，此決策平面為最優(yōu)分類超平面。

假設有l(wèi)個訓練樣本(x1,y1)，(x2,y2),…，(x l,y l)，其中x i∈R n，y i∈{+1,-1}，用于分類的超平面為(ω?x)+b=0。當H1與H2平面距離d=2/‖ ‖ω最大時，超平面才是最優(yōu)的，因此，SVM的關鍵問題由找到最優(yōu)分類超平面轉變?yōu)榻鉀Q相應的優(yōu)化問題。

當訓練樣本滿足線性可分條件時：

引入拉格朗日乘子αi,αi≥0，構造拉格朗日函數(shù)L。

求解得到的不為零的αi所對應的樣本點就構成了H1、H2平面，根據(jù)H1、H2就可以求出超平面，其對應的決策函數(shù)為：

當樣本不滿足線性可分條件時，就需要把樣本空間向高維空間進行映射，新空間的樣本能夠滿足線性可分的條件。這時為了求出決策函數(shù)就需要引用一個松弛變量?i,?i＞0，公式變?yōu)椋?/p>

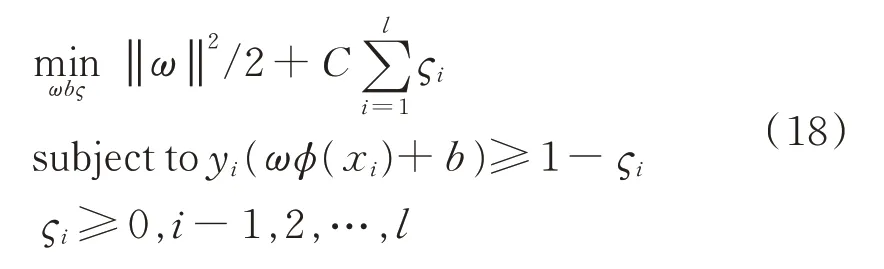
推導出決策函數(shù)表達式為：

式中，核函數(shù)為K(x i,x)=φ(x i)φ(x)，φ(x)為x i映射后的樣本。

SVM只能實現(xiàn)二分類，要想實現(xiàn)多分類，需要訓練多個二分類器。當分類個數(shù)為m時，對m類樣本中每2類訓練一個分類器，共需要m(m-1)/2個二分類器。對于一個未知樣本，需要經過所有的二分類器進行預測，最后通過投票決定樣本的最終類別。

4 實驗與分析

4.1 數(shù)據(jù)采集

本文所用數(shù)據(jù)皆為實測數(shù)據(jù)，采用Tektronix AWG70001任意波形發(fā)生器、Keysight E4438C ESG矢量信號發(fā)生器、2部Keysight N5172B X系列射頻矢量信號發(fā)生器和Keysight N5182B X系列射頻矢量信號發(fā)生器共5部輻射源來生成LFM信號。用實測信號來模擬真實的雷達信號，把5部輻射源分別命名為radar1、radar2、radar3、radar4、radar5。采集時設置帶寬為20 MHz，中心頻率為1 GHz，采樣頻率為25 GHz。每部輻射源采集120個脈沖信號，取其中80%的數(shù)據(jù)用于訓練，剩下的20%用來測試。

4.2 頻率估計誤差

利用FRFT算法進行了100次蒙特卡洛實驗來估計中心頻率，并計算估計出的頻率與采集信號時設定的頻率之間的誤差，如表1所示。

表1 中心頻率的估計結果

從表1中可以看出，采用FRFT方法來評估中心頻率誤差較小，可以用來作為中心點來劃分左右頻譜。

圖3是把估計的中心頻率作為特征進行識別的識別結果混淆矩陣，從圖中可以看出，識別率只有73%。表明5部信號發(fā)生器產生的信號中存在頻率漂移現(xiàn)象，但漂移量很小，僅僅以估計的中心頻率作為特征區(qū)分不出這5部輻射源。

圖3 識別率混淆矩陣

4.3 頻譜不對稱性仿真結果

在估計出中心頻率后，以估計出的中心頻率為中心，把信號的頻譜分為左頻譜和右頻譜2部分。

圖4—8展示了5部雷達輻射源個體左右頻譜的不對稱性。從圖中可以看出，頻譜的左右頻譜的對稱性已經被相位噪聲破壞，并且對不同輻射源的破壞程度是不同的。

圖4 radar1的頻譜不對稱性

圖5 radar2的頻譜不對稱性

圖9為5部雷達輻射源三個特征的聚類結果，可以看出，5部雷達輻射源的特征在小范圍內聚集，不存在特征交疊現(xiàn)象，說明這三個特征比較穩(wěn)定，可以利用這三個特征來進行個體識別。

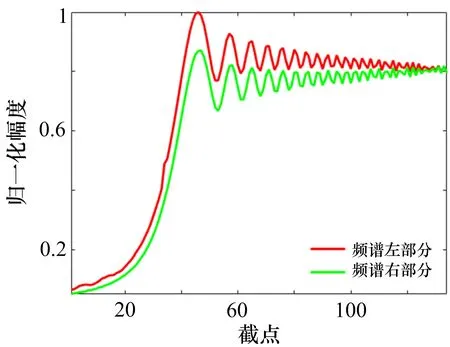
圖6 radar3的頻譜不對稱性

圖7 radar4的頻譜不對稱性

圖8 radar5的頻譜不對稱性

圖9 三個特征的聚類結果

給采集到的信號添加高斯白噪聲，并計算在不同的信噪比下，通過評估不對稱性進行個體識別的識別率。并與文獻[9]中提取VMD分解后奇異值作為特征的方法和文獻[10]中提取小波包能量作為特征的方法進行比較，仿真結果如圖10所示。

圖10 識別結果對比

從識別結果對比中可以看出，在信噪比為-5～20 d B的條件下，利用頻譜不對稱特征來進行個體識別方法的正確識別率高于文獻[9]和[10]中所提方法，尤其是在低信噪比情況下。本文所提方法在信噪比高于5 d B時，識別率可達到100%，即使信噪比在-5 d B時，正確識別率仍可達到90%，證明了基于頻譜不對稱性的方法對雷達輻射源個體有著很好的識別效果。

5 結束語

本文主要研究雷達輻射源個體特征提取與識別，首先分析了無意特征產生的機理，并針對信號的無意調制進行建模，發(fā)現(xiàn)無意調制會造成頻譜的不對稱，可以利用該特性來進行輻射源的個體識別。然后用FRFT算法來估計中心頻率，提取出左右頻譜，以左右頻譜的能量差、歐式距離和相關距離為特征，送入到SVM中進行識別。將仿真結果與其他特征提取方法對比，結果表明，本文所提方法在不同信噪比下都具有較好的識別效果。本文主要研究了LFM信號，對于其他脈內調制方式的信號還需要進一步研究。