各向異性拋物勢對非對稱高斯勢量子阱中強耦合極化子性質的影響
白瑞鋒,肖景林
(內蒙古民族大學 數理學院,內蒙古 通遼 028043)
0 引言
早期實驗發現,量子阱在阱的生長方向(z軸方向)比x軸方向和y軸方向的受限勢強得多[1-2],量子阱的生長方向(z軸方向)是強受限勢.量子阱的生長方向(z軸方向)的強受限勢問題在初期研究中沒有涉及.近些年有些學者[2]對量子阱的生長方向(z軸)存在強受限勢的量子阱的性質進行了研究.實驗要求量子阱的生長方向(z軸方向)肯定存在強受限勢,這一特性是在實驗中最先發現的.近年來理論工作者研究量子阱生長方向的強受限勢的性質,通過模擬計算和推導的理論方法尋找強受限勢,理論工作者終于找到了2種量子阱生長方向的強受限勢的形式,其一是非對稱高斯強受限勢,這一量子阱稱為非對稱高斯勢量子阱[3-4],另一種是非對稱半指數強受限勢,這一量子阱稱為非對稱半指數量子阱[4-6].在垂直于量子阱的方向存在一種受限勢比量子阱的生長方向的受限勢弱得多,是實驗中發現的,叫作各向異性拋物勢,實驗上早已發現是最接近晶體的真實勢.筆者采用的理論模型是在量子阱的生長方向存在非對稱高斯強受限勢而在垂直于阱的生長方向存在各向異性的拋物一般受限勢,研究這一量子阱的性質.最近筆者[7]研究了非對稱半指數量子阱中弱耦合極化子的基態能量,采用線性組合算符和幺正變換結合的方法,得到GaAs極化子的基態能量隨受限勢的2個正參數的變化關系,計算結果表明,半指數受限勢U和基態能量E0隨參數U0的增加而增大,隨參數σ的增加而減小.LIANG等[8]利用Pekar變分的強耦合方法導出了存在非對稱高斯勢量子阱的極化子的基態能量,第一激發態能量和躍遷頻率的溫度特性.并采用量子統計理論方法計算出極化子的態能和躍遷頻率與溫度和電子-聲子耦合強度之間的變化關系.發現當溫度增加時,極化子的態能和躍遷頻率增大.CAI等[9]利用線性組合算符和L.L.P.幺正變換方法,在理論上探索庫侖雜質勢和非對稱拋物受限勢對非對稱半指數量子阱極化子能級特性的影響.數值結果表明,找到在非對稱半指數量子阱中5種調節能級結構方式:變化庫侖雜質勢強度;非對稱拋物受限勢x和y方向有效受限強度和2個正參數.孫丙西等[10]根據線性組合算符和2次幺正變換方法研究了非對稱拋物受限勢對非對稱半指數量子阱中弱耦合極化子的基態結合能的影響,導出了GaAs非對稱半指數阱中弱耦合極化子的基態結合能隨x和y方向的非對稱拋物受限勢的受限強度和非對稱半指數受限勢的2個正參數的依賴關系.白瑞鋒等[11]采用同樣的方法,得出弱耦合極化子的振動頻率λ隨x軸和y軸方向的非對稱拋物受限勢的受限長度lx和ly的變化關系,振動頻率λ隨非對稱半指數受限勢的2個參數U0和σ的變化關系.通過上述的研究發現,通過模擬計算和理論推導,從理論方法上找到量子阱生長方向的強受限勢,還可以找到各向異性的拋物受限勢.自從HUYBRECHTS[12]對光學極化子的激發態進行研究之后,線性組合算符的方法就在學者們的理論研究中得到了廣泛的應用,此方法能夠對弱耦合極化子[13]以及強耦合極化子[14]進行研究,而且這也是唯一一種能夠對極化子振動頻率[5]進行計算的方法.第一性原理方法請見文獻[15].
然而,關于非對稱高斯勢量子阱中強耦合極化子的平均聲子數性質的研究甚少,筆者用線性組合算符方法,在非對稱高斯勢量子阱中,研究強耦合極化子的平均聲子數隨x方向和y方向各向異性拋物受限勢的受限強度、高斯勢阱的范圍和勢阱的高度的變化關系.
1 理論模型和計算
以RbCl晶體為例,在非對稱高斯勢量子阱中,x軸方向和y軸方向各向異性拋物勢,電子與體縱光學(LO)聲子相互作用.電子-聲子相互作用系統的哈密頓量可以寫成[13,16]
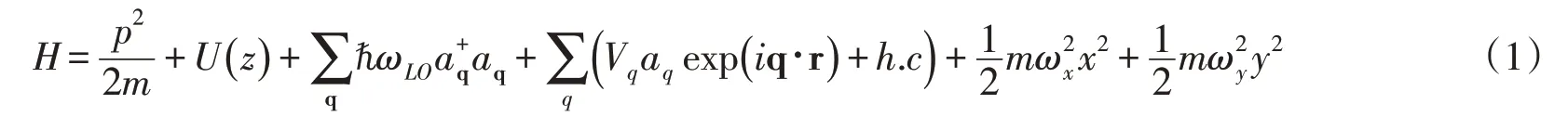
其中

m表示電子的帶質量,a+q(aq)是體縱聲子的產生(淹沒)算符. p 和r 是電子的動量和位置矢量.U(z)是非對稱高斯勢[13],z軸是量子阱的生長方向,R和V0分別表示高斯勢阱的范圍和勢阱的高度.方程(1)中的Vq和Vq中的α表示為

其中,α是電子-聲子的耦合強度.V為晶體的體積,ωLO為體縱聲子頻率.方程(1)中的最后2項分別表示x方向和y方向各向異性的拋物受限勢,其中,ωx和ωy表示受限強度.對哈密頓量(1)引進線性組合算符
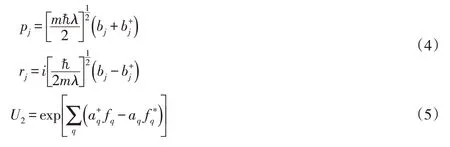
其中,fq(fq*) 是變分函數.
則哈密頓量變為

電子的基態波函數為

得出強耦合極化子的振動頻率滿足的方程為
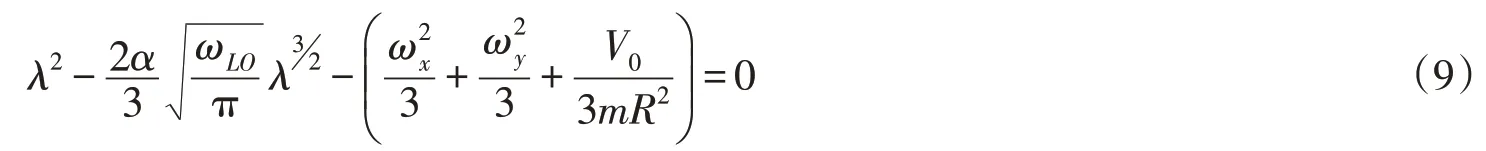
極化子的平均聲子數為

2 數值結果與討論
考慮RbCl非對稱高斯受限勢量子阱中,電子在垂直于阱的生長方向x方向和y方向的勢是各向異性拋物勢,以RbCl 晶體為例進行數值計算,所采用的實驗參量是?ωLO= 22.317 meV ,m= 0.432m0和α= 3.81[17]其計算結果表示在圖1和圖2中.
圖1展示了當受限強度ωx= 2.4 × 1013Hz 和ωy= 6.0 × 1013Hz 時,平均聲子數N隨高斯勢阱的范圍R和勢阱的高度V0的變化關系.圖1(a)表示N隨高斯勢阱的范圍R變化,圖1(b)表示N隨勢阱的高度V0的變化.圖1(a)中的點畫線分別表示勢阱的高度V0= 1.0 meV ,2.0 meV 和3.0 meV ,圖1(b)中的點畫線分別表示高斯勢阱的范圍R= 1.0 nm ,2.0 nm和3.0 nm.由圖1(a)和圖1(b)可以明顯看出強耦合極化子的平均聲子數是勢阱高度V0的增函數,而它是高斯勢阱范圍R的減函數.這一現象產生原因是阱的生長方向高斯強受限勢,隨著高斯強受限勢高度V0的增加,高斯強受限勢增大,這會導致極化子的平均聲子數增多.當高斯勢阱的范圍R增大卻發生相反的結果,其原因是隨著高斯勢阱范圍R的減少,高斯強受限勢增大,使極化子的平均聲子數增多.
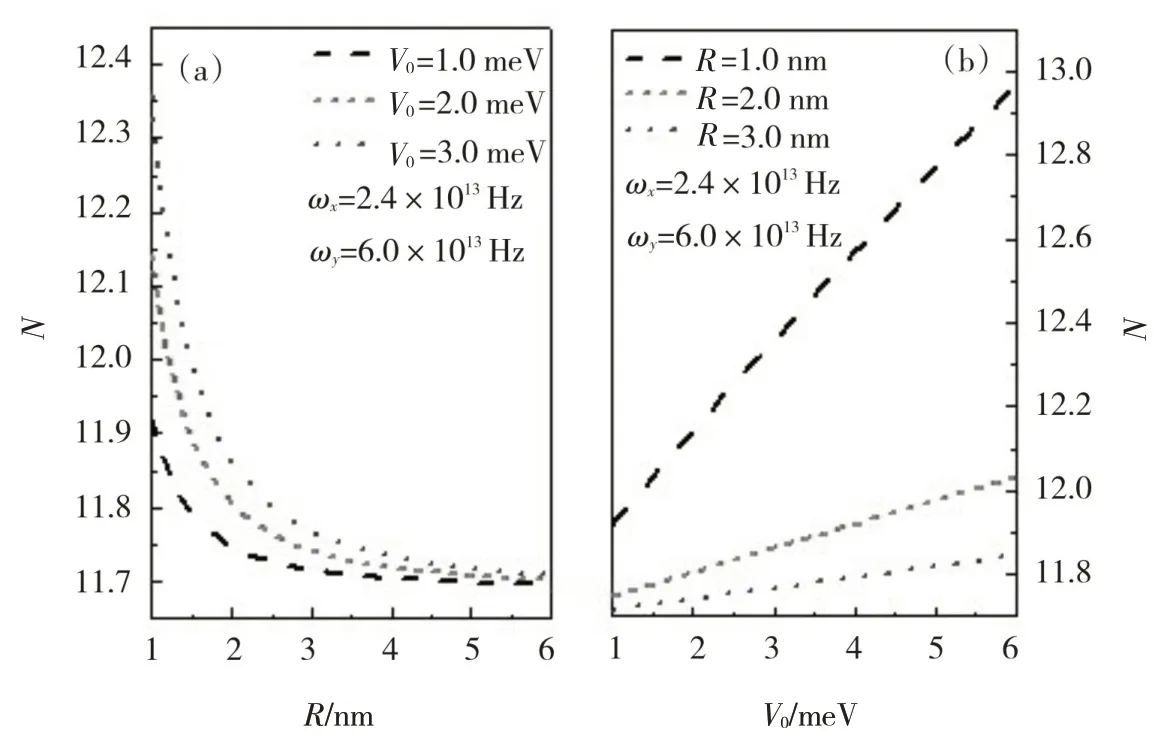
圖1 極化子的平均聲子數N 隨高斯勢阱的范圍R 和勢阱的高度V0的變化關系Fig. 1 Variation of mean phonon number N of polaron with the range R of the Gaussian potential well and height V0 of the potential well
圖2 研究了x軸方向和y軸方向的受限強度對極化子的平均聲子數的影響,取V0= 6.0 meV 和R= 2.4 nm,在圖2(a)中極化子的平均聲子數N作為各向異性拋物受限勢的x方向的受限強度ωx的函數,對于3 個不同各向異性拋物受限勢的y方向的受限強度ωy= 1.0 × 1013Hz,ωy= 2.0 × 1013Hz 和ωy= 3.0 × 1013Hz ,在圖2(b)中極化子的平均聲子數N作為各向異性拋物受限勢的y方向的受限強度ωy的函數,對于3 種不同各向異性拋物受限勢的x方向的受限強度ωx= 1.0 × 1013Hz ,ωx= 2.0 × 1013Hz 和ωx= 3.0 × 1013Hz .由圖2(a)和圖2(b)發現,當x方向和y方向的受限強度增大時,非對稱高斯量子阱中強耦合雜質極化子的平均聲子數增加,是因為受限強度的增大,導致受限勢寬度的減小,粒子運動范圍縮少,平均聲子數增大.

圖2 極化子的平均聲子數N 隨x方向和y方向各向異性拋物受限勢的受限強度ωx和ωy的變化關系Fig. 2 Variation of mean phonon number N of polaron with confinement strengths ωx and ωy of Anisotropic parabolic confinement potential in x and y directions
3 結論
在本研究工作中,研究了非對稱高斯強受限勢和各向異性拋物受限勢對非對稱高斯受限勢量子阱中強耦合極化子性質的影響.詳細分析了高斯量子阱中強耦合極化子的平均聲子數隨著勢阱的高度、高斯勢阱的范圍和x方向與y方向的受限強度的變化關系.數值計算結果展示,極化子的平均聲子數是高斯強受限勢勢阱高度和x方向與y方向的受限強度的增函數,而它是高斯勢阱的范圍的減函數.

