基于卡口數據的城市道路交通空間相關性分析
宋大創,馬曉旦,夏曉梅,孫明潔
(上海理工大學 管理學院,上海 200093)
0 引言
在城市道路系統中,某路段的交通狀態(如速度、流量)會受到其周圍路段交通狀態變化的影響。道路之間的這種交通依賴關系,通常被稱為道路交通空間相關性。對城市道路交通空間相關性進行探討,有助于理解城市道路系統的內部交互作用方式,并為交通插值和預測提供基礎。
現有研究及應用通常假定一定空間或拓撲距離內的道路具有交通空間相關性。例如:文獻[1]認為,一定距離內的道路具有空間相關性;文獻[2]中將一定時間內可達的路段視為交通相關道路;文獻[3]則假定一定拓撲距離內的道路具有空間相關性,并將其應用于交通預測;文獻[4]在交通數據插值時,使用拓撲距離來定義道路,并利用統計學中的相關系數法,確定研究區域內路段的互相聯系;文獻[5]為了獲取交通聯系的所有空間和時間相關性,采用了皮爾遜相關系數分析。結果表明,各路段的交通流量呈正相關關系,且不遵循任何距離模式。然而這些應用于快速路或高速公路的方法,在城市道路中并不太適用。眾多研究表明少部分城市道路承擔了絕大部分的交通流。交通流的傳播擴散也具有各向異性,上游路段的車輛不會均勻擴散到所有下游路段,而是會比較集中在某個或多個特定方向上,使得道路之間的交通相關性具有空間異質性[6-7]。因此在度量城市道路之間的相關性時,考慮其空間異質性是非常必要的。
本文從卡口數據中提取出研究路段的交通流時間序列,進行去時間趨勢分析,利用統計學中的相關系數法得到網絡權重矩陣,同時提取研究區域內每輛車行駛軌跡,形成流量轉移矩陣,再通過ochiai 系數(余弦相似性度量的一種形式),得到流量轉移權重矩陣。結合這兩個矩陣,重新度量不同路段之間交通空間相關性,進行短時交通流預測及效果比較,驗證方法的可行性和有效性。
1 城市道路交通空間相關性分析方法
從道路網絡上不同時間、不同地點觀測到的交通流,包括時間和空間的相關性。然而從歷史數據集提取的時間相關性,通常超過空間相關性,因為其比空間相關性更強烈[8]。因此,為了深入探討空間相關性,有必要去除交通流數據中時間趨勢的影響。
本文選取去除網絡空間平均趨勢的方法,即對每個檢測周期,計算待考察網絡中各節點流量的平均值。由于不同路段設計的通行能力不同,其流量趨勢也存在一定的比例關系。每個路段檢測到的流量,都按比例減去網絡平均流量,形成去趨勢后的路段流量時間序列。
(1)去時間趨勢分析
對于記錄的各路段流量時間序列qi?,i =1,...,N,其空間平均趨勢計算方法如式(1)所示。
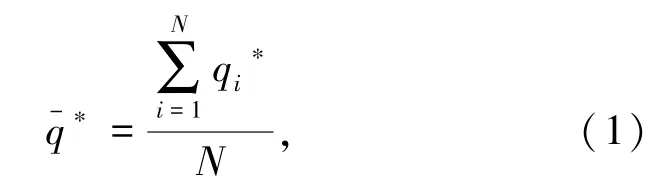
其中:N為研究區域內的總路段;為研究區域內空間平均趨勢;qi?為研究區域內各路段的流量時間序列。
設Ri為路段i在Nτ個采樣周期內流量總和與網絡所有節點在Nτ個采樣周期內流量總和之比,用于反映不同路段間流量日趨勢的比例。如式(2)所示。
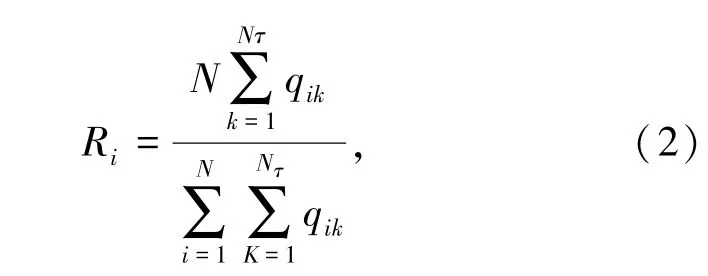
其中:qik為路段i在第k個采樣周期的流量,Ri為不同路段間流量日趨勢比例。
從各路段原始記錄流量序列中,按比例減去網絡空間平均趨勢,得到去趨勢后的流量時間序列,如式(3)所示。
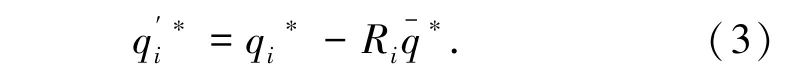
其中:為去時間趨勢后的流量時間序列。
(2)根據去趨勢后的流量時間序列,通過式(4),得到路段i與路段j之間的網絡權重矩陣。
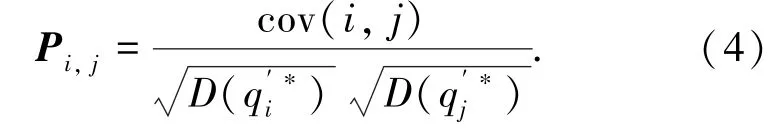
其中:cov(i,j)為的協方差,為的方差。
(3)提取每輛車的行駛軌跡,并建立流量轉移矩陣后,通過Ochiai 系數得到流量轉移權重矩陣。
①根據卡口設備收集到的車輛記錄,提取每輛車的行駛軌跡,定義如式(5)所示。
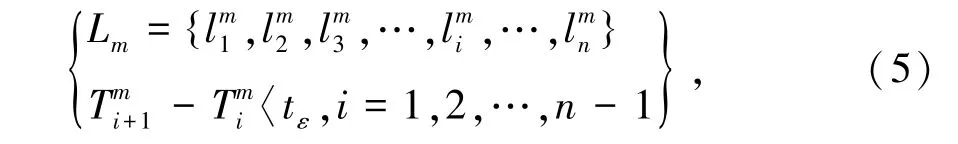
其中:Lm為第m連續通過的n個路段的路徑;為第m輛車通過第i個路段;為第m輛車通過第i個路段的時間;tε為時間閾值10 min。
②流量轉移矩陣表示為VTM∈RN×N。其中,N為研究區域考慮的交叉口的總進口道數。流量轉移矩陣構建過程如下:
Step 1提取每輛車c(1 ≤c≤m)在研究區域內的起點和終點;
Step 2提取每輛車經過的路段位置i(1 ≤i≤n-1),j(2 ≤j≤n);
Step 3。
上述VTM矩陣僅代表每個進口道流出的交通量,對于大多數城市道路而言,既有流出量也有流入量。因此,本文將流出量和流入量的總量作為兩個進口道間的總轉移量。最終的流量轉移矩陣可以結合其轉置矩陣定義,如式(6)所示:

VTM?矩陣中的元素值越大,說明車輛軌跡共享上下游的次數越多,其之間具有較強的交通空間相關性。
③通過Ochiai 系數(余弦相似性度量的一種形式)將交通流量轉移矩陣VTM?轉為i與j路段之間的流量轉移權重矩陣Q(i,j),如式(7)所示。

④為了識別與目標路段空間相關性最高的幾個路段,定義路段i與j之間的距離如式(8)所示。
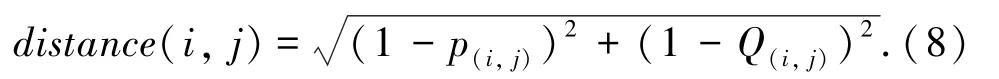
距離越小,說明路段i與j空間相關性越高。
2 實例分析
2.1 數據說明
本文實驗以某市城市道路卡口系統采集到的交通流數據為例,分析了不同路段之間空間相關性。選取9 個交叉口、36 個進口道、采集10 個工作日的交通數據。其中,前9 個工作日的數據為訓練數據,第10 個工作日的數據為預測數據。采集時間間隔為5 min。其空間關系如圖1 所示。

圖1 卡口檢測器位置Fig.1 Position of bayonet detector
2.2 預測結果比較
LSTM(Long Short Term Memory Network)長短時記憶網絡,是一種改進之后的循環神經網絡,在時間序列預測問題上有著廣泛的應用。
本文采用LSTM 模型進行多維單步預測,度量空間相關性的準確性。具體分為以下3 種情況:
(1)僅考慮研究路段與其對應的上游多維時空的交通流數據;
(2)考慮研究路段與其對應的上下游的多維時空交通流數據組合。
(3)根據本文的空間相關性度量方法,提取4個與研究路段空間相關性最高的路段,組成多維時空交通流數據組合。
本文假設某時段的交通流數據僅與其緊鄰的前3 個時段的數據具有較強的相關關系。采用LSTM預測模型進行短時交通流預測,選取MAE(平均絕對誤差)、MAPE(平均絕對百分比誤差)、RMSE(均方根誤差)進行預測誤差結果對比。以進口道A 為例,3 種情況預測比較結果見表1。
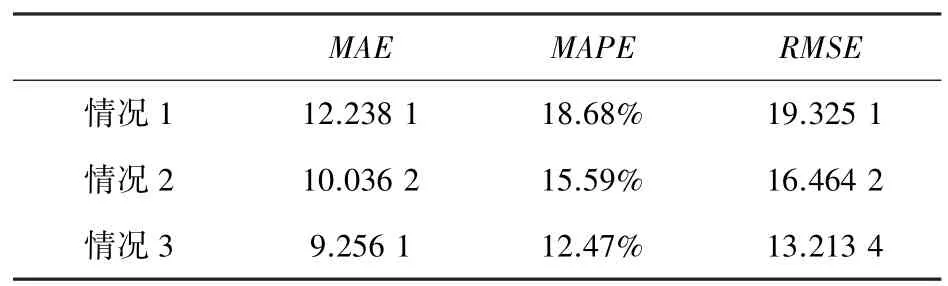
表1 不同情況下的預測結果Tab.1 Forecasting results under different conditions
從實驗結果可見,只考慮上游路段的情況下(情況1),預測精度最低;只考慮上下游路段(情況2)的預測精度其次;在考慮了空間異質性(情況3)的情況下,充分提取與研究對象道路交通空間相關性最高的路段,則預測精度最高。驗證了本文提出方法的有效性,為今后預測路網的交通流狀態提供依據。
2.3 空間相關性分析
根據本文提出的空間相關性分析方法,提取與路段A相關性最高的前4 個路段,其空間分布如圖2所示。從圖中可以看出,這些關聯的路段可以分為兩類:直接相連的路段(路段a、b)和非直接相連的路段(路段c、d)。對于前者,是目標路段A的交通量流入或流出方向,這些地點的交通狀況對目標路段A有直接影響;對于后者,雖然其之間的車輛過渡很少,但其交通量變化趨勢具有相似性。因此,本文提出的空間相關性分析方法既能反映車流量轉移關系,又能從統計角度捕捉交通流在空間上相似的趨勢。
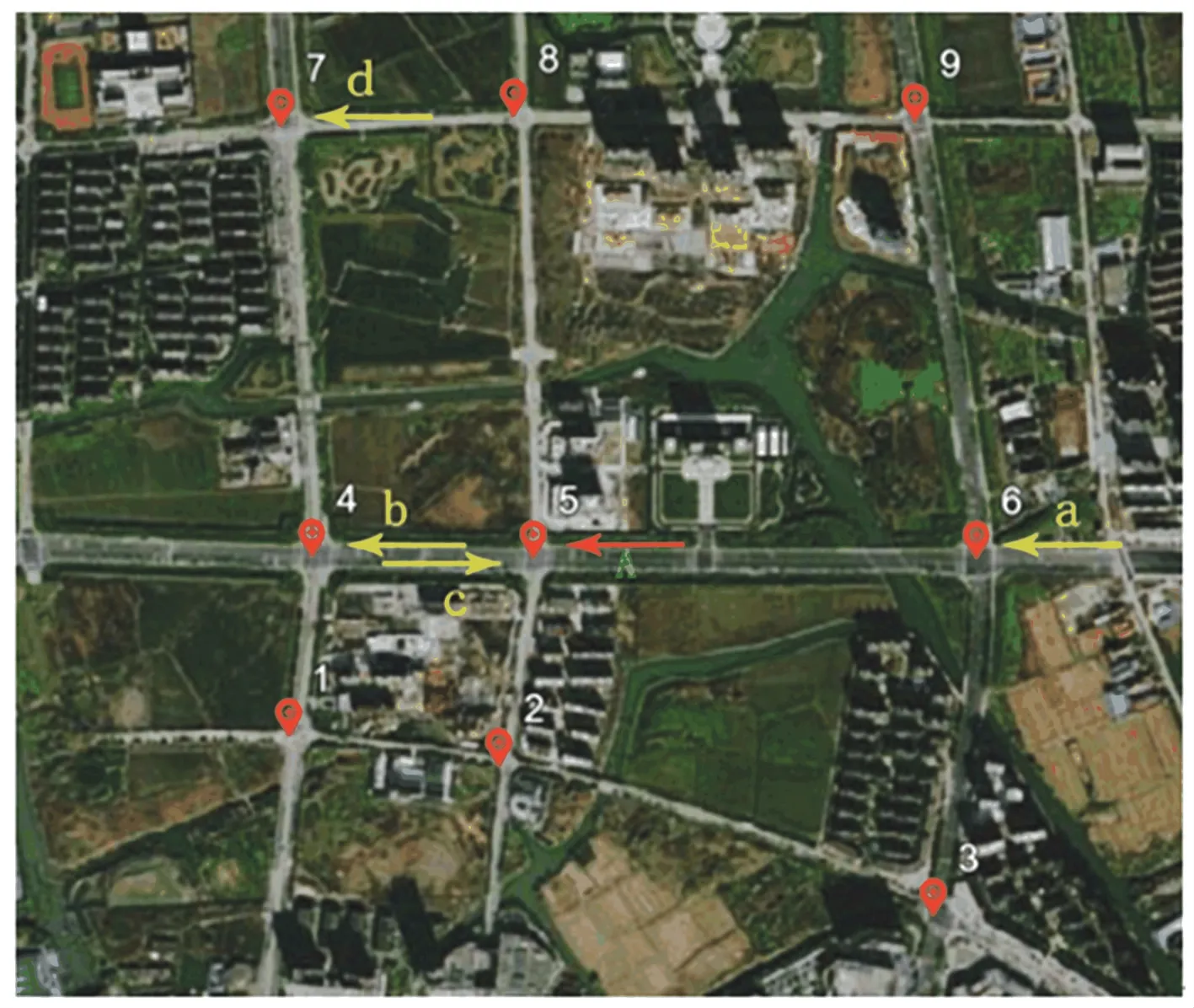
圖2 與進口道A 相關性最高的前四個路段空間分布Fig.2 Spatial distribution of the first four sections with the highest correlation with inlet road A
3 結束語
機動車的出行不但構成了整個路網的交通分布模式,也是道路之間產生交互影響和交互作用的根本原因。本文結合車輛軌跡得到的流量轉移權重矩陣和不同卡口數據量化的網絡權重矩陣,構造一個新的網絡權重矩陣,較準確地描述了城市道路之間的交通空間相關性,為以后能更好更快的預測路網上的交通流狀態提供依據。

