自適應懲罰薄板樣條回歸模型

丁夢珍

（安徽科技學院信息與網絡工程學院，安徽滁州233100）

1 引言

回歸模型主要分為參數模型和非參數模型[1]，當回歸函數的形式已知，而參數未知，則該模型為參數回歸模型，參數方法雖然比較簡單明確，但是缺乏一定的靈活性，如果實際模型與假定相背離，那么建立的模型對實際指導毫無意義，為了使模型具有更廣泛的適用范圍，非參數模型應運而生，該方法無需預先假定回歸函數的形式，而是基于數據結構去估計回歸函數，因而適應數據變化的能力更強，具有良好的穩健性.現在人們研究比較多的非參回歸擬合方法主要包括：核估計、局部多項式估計、樣條估計、正交級數估計和小波估計等[2].在眾多的估計方法中，樣條估計依其靈活性和穩定性占據著重要的位置，如回歸樣條、光滑樣條、懲罰樣條等，而懲罰樣條估計又在樣條法中有著舉足輕重的作用.懲罰樣條最早由Eilers、Marx（1996）[3]提出，當時是為了解決廣義線性光滑問題，現在已擴展到多個方面，如廣義可加模型、變系數模型等，其基本思想是在目標函數中加入B樣條基函數系數的差分作為懲罰項，主要用于解決高階樣條基函數計算的復雜度或估計的不可控問題.

懲罰樣條估計能得到廣泛的應用：一方面是由于可以使用較少的節點構造基函數，從而降低計算工作量，另一方面是其具有良好的高維擴展性.由J.Duchon（1977）[4]提出的薄板樣條是一元樣條到多元樣條的非張量積形式的推廣.在經典的懲罰薄板樣條回歸模型中，對每個基函數系數施加的懲罰權重是一樣的，然而當數據具有強烈的局部變化特征時，這種等權重性懲罰使得模型的擬合效果不理想，因此如何提高模型的局部自適應性成為一個熱門的研究課題[5].探究該問題的思路主要包括兩種，其一是基于薄板樣條基函數的節點個數和位置的優化選擇[6]，其二是針對不同基函數系數的局部懲罰權重的優化選取[7].本文基于第二種思路展開探索，通過分析薄板樣條基函數的空間幾何意義，引入數據的局部縱向極差的變式來表示數據的局部變化特征[8]，以此構造局部懲罰權重并嵌入到回歸模型的懲罰項當中.這種方法結合了數據的局部變化特征和基函數的幾何意義，使得模型的懲罰權重由局部數據所驅動，從而具有局部特性.相比于經典的懲罰回歸模型，該模型更適用于具有明顯的局部波動特征的數據.模型的估計流程類似于經典的嶺回歸估計[9]，參數求解簡單.由函數模擬的結果表明該方法的自適應特征是非常有效和顯著的，提升了模型的擬合精度.本文的第二部分內容對自然薄板樣條回歸模型和懲罰薄板樣條回歸模型作一簡介；第三部分內容根據樣條基函數的幾何意義引入了自適應懲罰薄板樣條回歸模型；第四部分內容給出相應模型的函數模擬例子；最后部分內容對全文進行總結.

2 薄板樣條回歸模型

2.1 自然薄板樣條回歸模型

假設有n對觀測數據{（ti，yi），i=1，2，…，n}，則非參數回歸模型如（1）式所示[10]，

并假設E[ε|t]=0，E[y|t]=0，將看作關于二元變量t∈[a，b]×[a，b]的待估光滑函數.薄板樣條g通過最小化（2）式來估計f，

其中y=（y1，y2，…，yn）′，g=（g（t1），g（t2），…，g（tn））′，懲罰函數J（g）用來度量回歸函數的粗糙程度，調節參數λ控制回歸函數的擬合優度與光滑度之間的平衡.二維空間上基于二階偏導數的粗糙度懲罰項被定義為

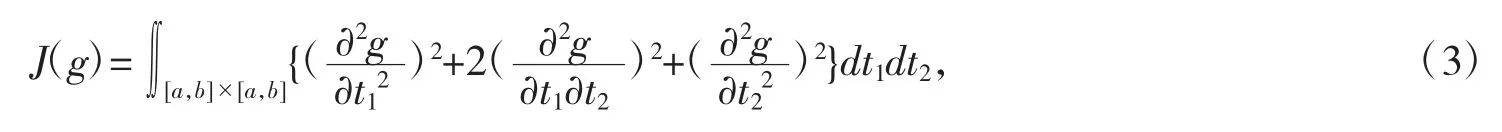
則滿足（2）式最小的薄板樣條函數g（t）形式如下

式中δ=（δ1，δ2，…，δn）′和α=（α1，α2，α3）′為待定系數向量且滿足約束條件Tδ=0，T為3×n矩陣，其元素Tij=?j（tk），?1，?2，?3為二維空間上次數小于2的多項式構成的三維空間的一組基.||·||表示歐幾里得范數，η（·）是薄板樣條的核函數，其采用以下形式

現定義n階方陣E，其元素為Eij=||η（ti-tj）||.則該模型擬合的目標函數為

且滿足Tδ=0，則系數向量的估計值可由方程組（6）唯一確定

求得

其中Tr（Hλ）是帽子矩陣的跡，則使得GCV（λ）取到最小的λ值即為最優取值.

2.2 懲罰薄板樣條回歸模型

自然薄板樣條回歸模型將粗糙懲罰思想推廣到二維空間，放寬了多個解釋變量的線性假定，使模型在假定方面具有更強的適應性，是一般線性模型的全面擴展.但該模型是多個樣條變量的非參數回歸分析，如果使用全部樣本作為節點，在應用時會增加不必要的工作量，這就要求通過降低節點個數即基函數維數來重新構造回歸模型，即懲罰薄板樣條回歸模型.

此時薄板樣條函數形式如下：

其中κ1＜κ2＜…＜κK為[a，b]×[a，b]上均勻選定的節點，則懲罰薄板樣條回歸模型的擬合目標函數為：

3 自適應懲罰樣條回歸模型

由（10）式中的懲罰矩陣S的構造可知，該矩陣未考慮數據在縱向上的變化特征，且總調節參數λ對每個基函數系數δ1，δ2，…，δK的懲罰權重是相同的，同樣也忽略了數據在縱向上的局部波動特征，因而懲罰薄板樣條回歸模型對數據的估計缺乏自適應性，而當數據在縱向上的變化有明顯的局部特征時，該回歸模型就難以捕捉到這些信息，進而導致擬合效果不理想.為了彌補該缺陷，本文提出一種改進的方法，其思想是將數據的局部縱向的變化特征添加到懲罰矩陣S當中，使得懲罰矩陣包含數據在縱向上的局部變化特征，該方法稱之為自適應懲罰薄板樣條回歸模型，下面給出具體過程.

通過分析薄板樣條的第k個節點位置的基函數δiη（||t-κi||）可知，該函數是關于二元變量t的凸函數，系數δK的符號決定了該曲面開口的方向，數值控制了開口的大小.|δk|越大，開口越小，曲面越尖銳，反之則開口越大，曲面越平坦.因此|δk|越大時，δiη（||t-κi||）能充分地擬合波動較劇烈的數據，反之則能精準地擬合波動較平緩的數據.從而在懲罰回歸模型中，在數據波動較大的區域給予薄板樣條系數較小的懲罰權重是合理的，反之則應給予薄板樣條系數較大的懲罰權重，這種處理方式能夠使得薄板樣條在全局上準確地反映出數據的變化特征，從而增強模型的自適應性，提高模型的擬合精度.

基于上文分析，我們引入局部懲罰權重向量ω=（ω（κ1），…，ω（κK），0，…，0），并記

將（10）式中的β乘以W，此時模型擬合的目標函數為

式中P=W′SW，下面討論如何選取懲罰權重向量ω.根據上文所述，懲罰權重應當設置成數據在縱向上的局部變化幅度的單調遞減函數，本文采用以節點為中心的圓域內的數據在縱向上的極差來反映該位置的局部波動幅度，具體表達式如下：

進而構造該極差的單調遞減函數

正數q用來調節懲罰權重的力度，依然根據懲罰最小二乘估計得

4 模擬

本節將給出幾個具有代表性的數值模擬實例，根據擬合等高線圖和統計指標來進一步說明基于本文提出的方法相比自然薄板樣條（full spline）、懲罰薄板樣條（p-spline）和tprs[6]的擬合效果的優良性.所有計算和作圖均在R3.2.1中實現.

例1光滑函數表達式為

樣本分布在[0，1]×[0，1]區域內的24×24均勻網格上，其所對應的響應變量為yi=f（xi，zi）+εi，且εi~N（0，0.052），懲罰樣條的節點選擇在區域內12×12均勻網格上，薄板回歸樣條的節點個數為144.一次隨機試驗結果的真實等高線及基于四種模型的擬合等高線如圖1所示.

圖1描繪了真實函數的等高線圖及基于四種方法的擬合等高線圖，通過對比可以清晰地發現，基于自適應懲罰薄板樣條方法的擬合函數相對平滑一些，在邊界處擬合效果的優勢更加顯著，且在總體上能夠較準確地估計出真實函數的走勢.另外引入統計指標均方誤差MSE作為度量準則，即MSE值越小模型的擬合效果越好.

圖1 （a）為真實函數的等高線，（b）為基于自然薄板樣條回歸模型的擬合等高線，（c）為基于懲罰薄板樣條回歸模型的擬合等高線，（d）為基于自適應懲罰薄板樣條的擬合等高線，（e）基于tprs的擬合等高線.

為了盡可能降低隨機因素對估計的影響，我們進行了100次獨立重復試驗并給出了MSE箱線圖，如圖2所示，顯然本文提出的方法的回歸效果更理想.

圖2 100次獨立重復實驗下，基于自然薄板樣條擬合、懲罰薄板樣條擬合、tprs擬合與自適應懲罰薄板樣條擬合的MSE箱線圖.

例2光滑函數表達式為：

其中δx=0.3，δy=0.4，樣本分布在[0，1]×[0，1]區域內的24×24均勻網格上，其所對應的響應變量為yi=f（xi，zi）+εi，且εi~N（0，0.12），懲罰樣條的節點選擇在區域內12×12均勻網格上，薄板回歸樣條的節點個數為144.一次隨機試驗結果的真實等高線及基于四種模型的擬合等高線如圖3所示.

圖3 （a）為真實函數的等高線，（b）為基于自然薄板樣條回歸模型的擬合等高線，（c）為基于懲罰薄板樣條回歸模型的擬合等高線，（d）為基于自適應懲罰薄板樣條的擬合等高線，（e）基于tprs的擬合等高線.

圖3描繪了真實函數的等高線圖及基于四種方法的擬合等高線圖，可見基于自適應懲罰薄板樣條方法的擬合等高線明顯比較平滑，有效地避免了過度波動，能夠較準確地估計出真實等高線的走勢，在整體上與真實等高線更加吻合.此外，四種估計方法的MSE箱線圖如圖4所示，說明本文所提出的方法在估計精度上優于另外兩種估計方法，擬合效果更加理想.

圖4 100次獨立重復實驗下，基于自然薄板樣條擬合、懲罰薄板樣條擬合、tprs擬合與自適應懲罰薄板樣條擬合的MSE箱線圖.

例3光滑函數表達式為

樣本分布在[0，1]×[0，1]區域內的24×24均勻網格上，其所對應的響應變量為yi=f（xi，zi）+εi，且εi~N（0，0.52），懲罰樣條的節點選擇在區域內15×15均勻網格上，薄板回歸樣條的節點個數為225.一次隨機試驗結果的真實等高線及基于四種模型的擬合等高線如圖5所示.

圖5描繪了真實函數的等高線圖及基于四種方法的擬合等高線圖，直觀上看，基于自適應懲罰薄板樣條方法的擬合等高線更加接近于真實曲線，不規則的波動會減弱，光滑度得到顯著的提高.另外，圖6給出了四種估計方法的MSE箱線圖，顯然本文提出的方法的MSE減小的幅度非常明顯，取得了較好的擬合效果.

圖5 （a）為真實函數的等高線，（b）為基于自然薄板樣條回歸模型的擬合等高線，（c）為基于懲罰薄板樣條回歸模型的擬合等高線，（d）為基于自適應懲罰薄板樣條的擬合等高線，（e）基于tprs的擬合等高線.

圖6 100次獨立重復實驗下，基于自然薄板樣條擬合、懲罰薄板樣條擬合、tprs擬合與自適應懲罰薄板樣條擬合的MSE箱線圖.

例4光滑函數表達式為

樣本分布在[-10，10]×[-10，10]區域內的24×24均勻網格上，其所對應的響應變量為yi=f（xi，zi）+εi，且εi~N（0，0.52），懲罰樣條的節點選擇在區域內12×12均勻網格上，薄板回歸樣條的節點個數為144.一次隨機試驗結果的真實等高線及基于四種模型的擬合等高線如圖7所示.

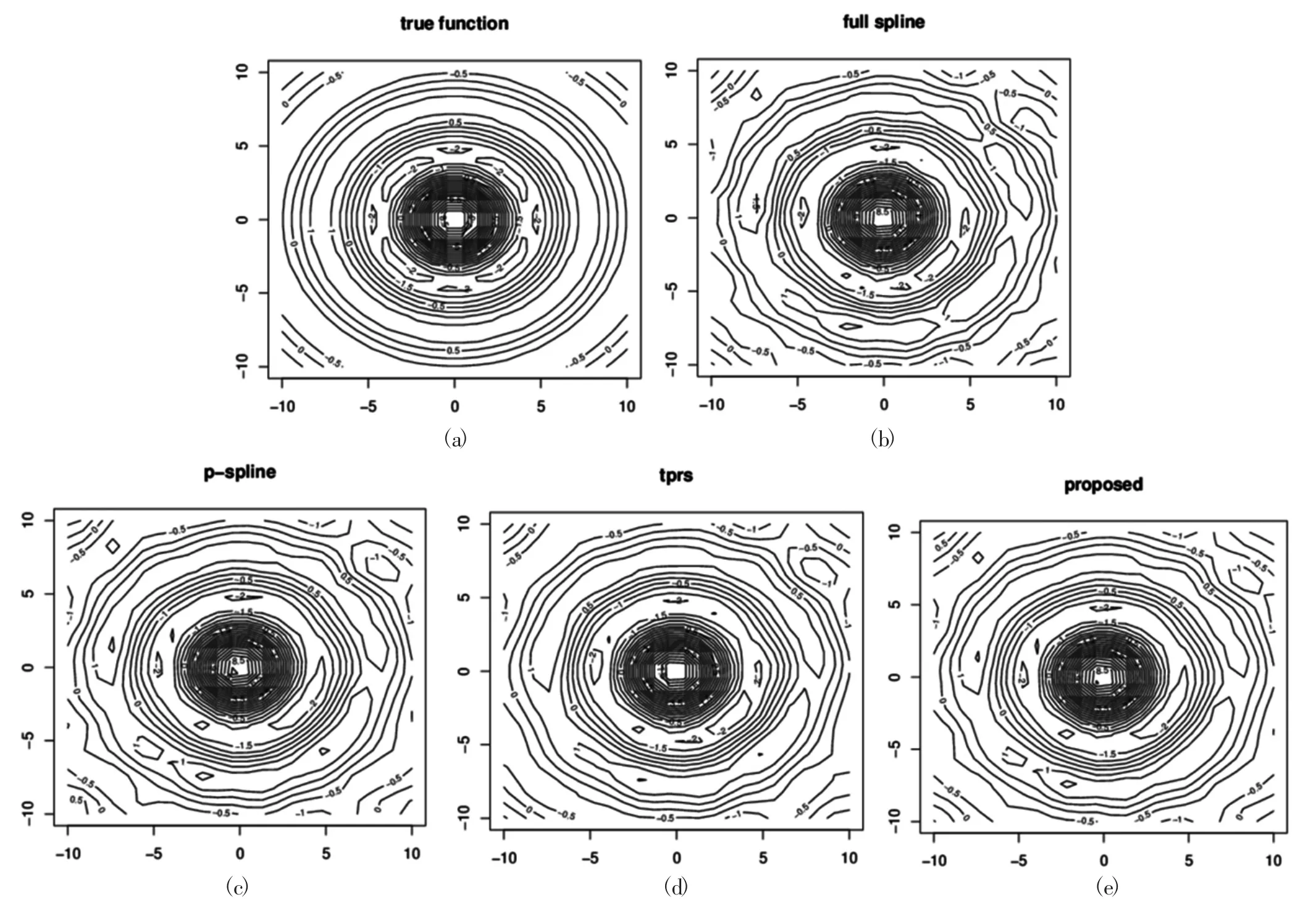
圖7 （a）為真實函數的等高線，（b）為基于自然薄板樣條回歸模型的擬合等高線，（c）為基于懲罰薄板樣條回歸模型的擬合等高線，（d）為基于自適應懲罰薄板樣條的擬合等高線，（e）基于tprs的擬合等高線.

圖7描繪了真實函數的等高線圖及基于四種方法的擬合等高線圖，從中可以發現基于自適應懲罰薄板樣條方法擬合的線條更加光滑，與真實等高線有著較好的重合.此外，圖8畫出了四種估計方法的MSE箱線圖，表明本文提出的方法的估計精度比較高，能夠準確地模擬出函數真實走勢.綜上所述，不管是考察統計指標MSE還是觀測圖形，基于自適應懲罰薄板樣條估計都是一種比較理想的估計方法.

圖8 100次獨立重復實驗下，基于自然薄板樣條擬合、懲罰薄板樣條擬合、tprs擬合與自適應懲罰薄板樣條擬合的MSE箱線圖.

5 總結

如何提高回歸模型的擬合精度是一個相當有意義的研究課題，本文通過增強模型的自適應性能力的途徑來提高精度.文中提出了自適應懲罰薄板樣條回歸模型，該方法的局部懲罰權重是由節點周圍區域內部分數據的縱向極差的遞減函數所生成，并將其嵌入到經典懲罰回歸模型的懲罰項中.其創新點在于當數據在局部區域內波動幅度較大時，模型能夠給予擬合曲面較小的懲罰權重，而當數據在局部區域內波動幅度較小時，則能夠給予擬合曲面較大的懲罰權重，從而由數據驅使的懲罰權重可以提升模型的自適應性，進而提高模型的擬合精度.模擬結果顯示，基于極差調節的局部懲罰權重的回歸模型的擬合曲面能夠較精準地反映數據的局部變化特征，使得擬合曲面和真實曲面更吻合.