河南省商品房價格影響因素的統計分析
張慶春 肖夢蝶 范曉東
一、引言
隨著社會經濟的快速發展,商品房價格持續上漲,房地產業也逐漸變為熱點話題。分析商品房價格變動的影響因素具有重要的現實意義,既可以幫助政府調控經濟,也可以幫助房地產商把握市場動向。基于多元線性回歸分析模型,2014年,李生彪考慮了人均收入、人口數量、商品房平均投資成本和一年期定期存款利率對蘭州市商品房價格的影響;2018年,薄鑫和孫英雋研究了商品房銷售面積、房地產開發企業住宅竣工房屋面積、居民消費價格指數CPI和新建住宅銷售價格指數對西安市商品房價格的影響。基于方差分析模型,2011年,年超等研究得出影響北京市商品房平均銷售價格的因素是所在區縣、所處環線和裝修類型以及有無地鐵。本文以河南省為例,綜合運用方差分析模型和多元線性回歸分析模型,對商品房價格影響因素進行了實證分析。
二、模型的建立與求解
1.方差分析模型的建立
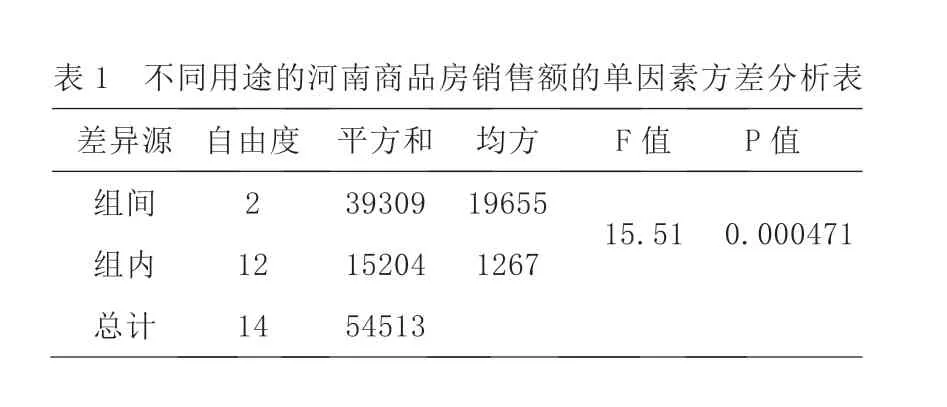
我們將商品房用途作為因素,考慮河南省商品房價格的影響。選取河南省商品房2015—2019年按辦公樓、別墅和高等公寓及其他商品房分類的銷售額(數據來源國家統計局)。以住宅用途作為自變量,各類住宅銷售額作為因變量進行單因素分析。
?
因為P=0.000471=0.05,所以拒絕原假設H0,即有證據表明不同用途的商品房銷售額有顯著差異。
2. 多元線性回歸分析模型的建立
選取河南省2009—2018 年的住宅商品房平均價格、人均地區生產總值和城鎮化率的數據(數據來源國家統計局)。以商品房平均價格為因變量y,以人均地區生產總值、城鎮化率分別為x1、x2,首先分析因變量和兩個自變量間的相關關系,畫出它們的散點圖,如下圖所示。
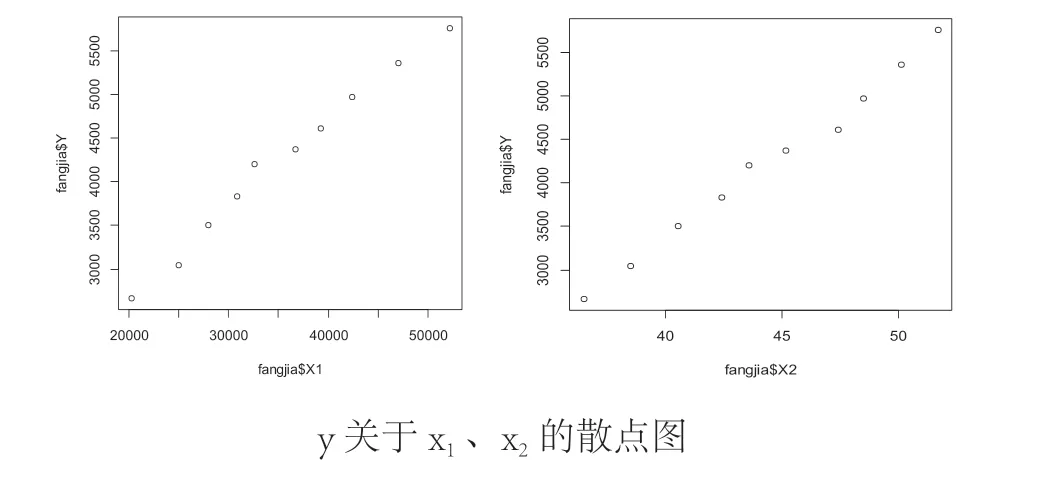
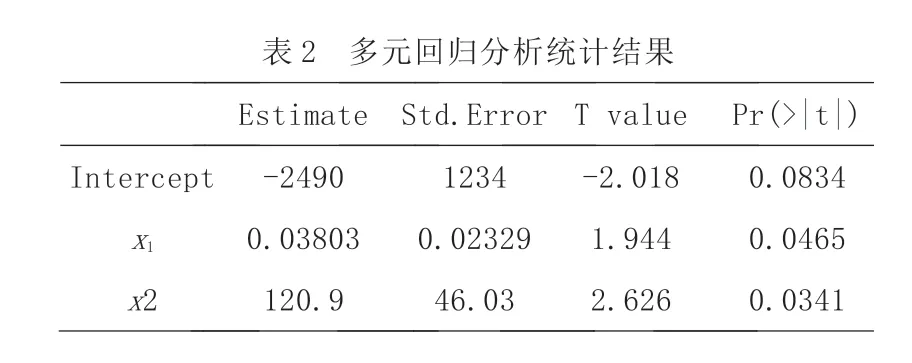
由上圖可以看出,因變量y 與自變量x1和x2之間都具有線性相關性,因此可以建立多元線性回歸分析模型,利用R 軟件進行計算,回歸統計結果見表2。
?
經計算F統計量的P值為2.166e-08<0.05,說明因變量和兩個自變量之間的線性關系顯著;又由表2中回歸系數的P值均小于0.05,說明多元線性回歸分析模型的系數都是顯著的。由此可以得到多元回歸估計方程為y=-2490+0.03803x1+120.9x2。經計算得到多重判定系數為0.9935,表明商品房價格的變差中被估計的回歸方程所解釋的比例為0.9935,說明多元線性回歸分析模型擬合效果良好。
三、結語
本文基于方差分析模型和多元回歸分析模型,分析了河南省商品房價格影響因素。利用方差分析模型對不同用途的商品房銷售額進行分析得出:不同用途的商品房銷售額有顯著差異;通過分析商品房價格(y)與人均地區生產總值(x1)和城鎮化率(x2)的相關關系建立多元線性回歸分析模型,得到估計的回歸方程y=-2490+0.03803x1+120.9x2。
這表明:商品房價格與人均地區生產總值和城鎮化率均成正相關。在城鎮化率不變的情況下,人均地區生產總值每增加1元,商品房價格平均增加0.03803億元;在人均地區生產總值不變的情況下,城鎮化率每增加1個百分比,商品房價格平均增加120.9元。多元線性回歸分析模型通過了顯著性檢驗,并且由多重判定系數可知多元線性回歸分析模型擬合效果良好,結論可為相關部門提供參考依據。

