現代有軌電車線路扣件系統模態與鋼軌波磨關系研究

張 昭，楊新文，馬骙骙，趙治鈞，陸文學

(1.同濟大學軌道交通結構耐久與系統安全上海市重點實驗室，上海 201804；2.同濟大學道路與交通工程教育部重點實驗室，上海 201804；3.蘇州市軌道交通集團有限公司，江蘇，蘇州 215004)

現代有 軌電車具有節能、環保、投資少、易建設、景觀效果好等優點[1]，截至2020年6月30日，中國內地累計17個城市投運現代有軌電車線路共429.93 km，占城市軌道交通運營總里程的6.21%[2]。出于路權共享的考慮，現代有軌電車路基段多采用嵌入式軌道[3]，隨著運營時間的增加，由此產生的路面開裂、軌面沉降、棱邊破損等病害[4]以及扣件罩破損、彈條斷裂、軌下墊板失效等隱蔽病害，這些病害將會對行車平穩性與安全性、軌道及路面的壽命造成不利影響。

鋼軌波磨是輪軌系統中常見的一種損傷，在不同鐵路運輸系統中均有出現。現代有軌電車線路上的鋼軌波磨多是短波長波磨(波長25 mm～80 mm)[5]，如圖1所示，出現在綠化與路基線路的曲線段和上坡段。現代有軌電車的運行速度可在30 km/h～70 km/h變化，通過短波波磨區段時，會引起車輛-軌道系統的中高頻振動，列車通過頻率與彈條固有頻率接近時，彈條振動加劇，易產生振動疲勞[6]，導致彈條扣壓力下降，甚至造成彈條疲勞斷裂。

圖1 有軌電車線路槽型軌波磨Fig.1 Groove rail corrugation of tram lines

彈條疲勞斷裂現象在地鐵線路中出現較多，這一病害在北京地鐵及深圳地鐵線路中均有出現。針對彈條破壞機理，為了準確分析彈條在安裝狀態及工作狀態下的力學特性，鋼軌-扣件系統精細化有限元模型被廣泛應用于相關研究中[7?9]。諸多學者通過對鋼軌-扣件系統進行動力學分析及現場測試[10?11]，研究彈條的動力響應及疲勞特性[12]，驗證了彈條振動疲勞是彈條破壞的主要原因之一。

王平等[6]通過對深圳地鐵有無波磨區段的彈條振動加速度進行現場測試，分析彈條振動的時頻特性，并建立扣件系統振動疲勞模型，得出當列車通過頻率與彈條固有頻率吻合時，會降低彈條的疲勞壽命，驗證了振動疲勞理論在軌道交通扣件系統彈條疲勞斷裂機理領域應用的可能性。尚紅霞等[13]通過有限元方法，表明Ⅲ型彈條斷裂與安裝狀態有很大關聯，隨著彈條發生疲勞斷裂，會導致輪軌作用力加劇，加速其他結構破壞。

國內外現有研究多基于發生彈條斷裂的實際工程問題進行破壞機理與結構動力響應分析，缺乏對于彈條固有頻率、列車通過速度、波磨波長等相關因素的系統分析及彈條振動疲勞破壞發生的預防措施研究。

目前，在現代有軌電車線路中仍未出現彈條斷裂的現象，這是由于相較地鐵線路，現代有軌電車的運量小、累積運營時間短、運行時間間隔大，因此彈條斷裂這種極端病害還未出現，但隨著運營時間的增加，一旦在有軌電車嵌入式軌道區段發生彈條斷裂病害，則會帶來病害檢測不便、維修成本高、影響行車安全等諸多不利，所以對彈條斷裂的發生原因的系統分析及預防是有必要的。

本文主要研究由振動疲勞機理引起的彈條斷裂問題，利用ANSYS有限元分析軟件建立現代有軌電車鋼軌-扣件系統精細化模型，進行考慮安裝預應力的模態分析，得出鋼軌-扣件系統在不同軌下剛度下的彈條固有頻率及可能破壞形式，再與列車通過頻率做統計對比分析，確定彈條破壞出現對應的列車速度及波磨波長匹配關系，以期為現代有軌電車系統彈條振動疲勞斷裂的預防及檢測提供建議。

1 現代有軌電車扣件系統

1.1 YGⅠ-1扣件系統

YGⅠ-1扣件(圖2)為無螺栓彈性分開式扣件，適用于有軌電車系統整體道床線路，所采用的彈條為“e”型彈條，直徑為16 mm。

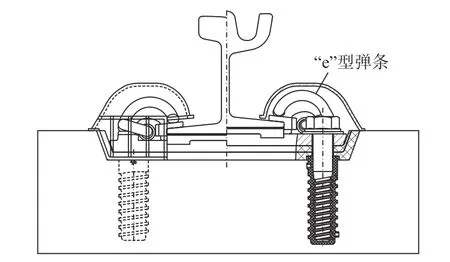
圖2 YGⅠ-1扣件系統組裝圖Fig.2 Assembly drawing of YGⅠ-1 fastener system

1.2 典型彈條斷裂形式

“e”型彈條包括中肢、小圓弧、跟端、大圓弧和趾端5個部分，通過對地鐵線路“e”型彈條斷裂的現場觀察[14?15]，典型彈條斷裂形式如圖3所示，主要有小圓弧近中肢處(圖3(a))、小圓弧近跟端處(圖3(b))、大圓弧近跟端處(圖3(c))3種斷裂形式。

圖3 “e”型彈條典型斷裂形式圖Fig.3 Typical fracture type diagram of "e"type rail clip

現代有軌電車線路中雖無彈條斷裂病害發生，但對于同樣采用“e”型彈條的YGⅠ-1扣件系統，彈條在車輛-軌道系統中受力情況與地鐵線路中相似，故以地鐵線路中彈條典型斷裂形式作為有軌電車線路可能發生的彈條斷裂形式。

2 有限元模型

利用ANSYS有限元軟件建立鋼軌-扣件系統精細化模型如圖4所示。YGⅠ-1扣件系統零部件較多，本文主要在考慮安裝預應力條件下對彈條進行模態分析，簡化螺旋道釘、尼龍套管及扣件罩等對分析影響較小的部件，并通過施加相應的約束來等效替代其限位、固定的功能。模型包括槽型軌、軌下墊板、軌距塊、彈條及鐵墊板5個部分，其中彈條采用四面體單元網格，其余部件采用六面體單元網格，模型建立如圖4(a)所示，扣件間距為0.6 m。

在扣件系統安裝中，各部件之間的接觸狀態隨著結構受力變化也發生改變，產生的非線性接觸問題需要通過設置合適的接觸單元來模擬。各組接觸對之間采用面-面接觸，軌距塊的主要作用是保持軌距，對鋼軌有水平限位作用，設置為粗糙接觸模式。其余部件之間均為摩擦接觸，金屬材料與金屬材料之間的摩擦系數取0.15，與非金屬材料之間的摩擦系數取0.8。彈條中肢固定約束處理，其根部距圓孔端10 mm，彈條趾端下表面與軌距塊上表面、彈條跟端下表面與鐵墊板上表面均存在接觸，如圖4(b)所示。

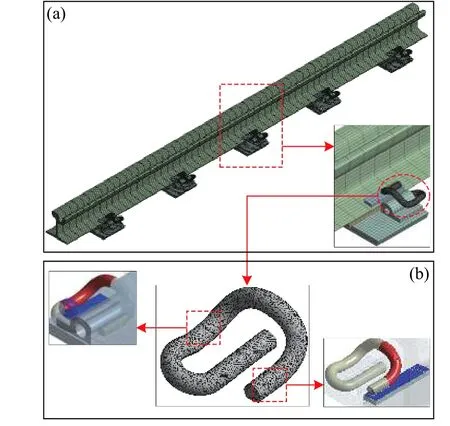
圖4 鋼軌-扣件系統有限元模型Fig.4 Finite element model of rail fastener system

彈條材料為60Si2MnA彈簧鋼，考慮到彈條在安裝時局部位置會發生塑性變形，彈條材料的應力-應變關系采用理想線性強化彈塑性材料本構模型，強化模量可設置為 E′=0.1E[16]，下屈服強度為1375 MPa，抗拉強度為1570 MPa，可得如圖5所示雙線性等向強化模型。其中軌下墊板剛度彈性模量隨剛度變化如表1所示，模型各部件所用材料參數見表2。

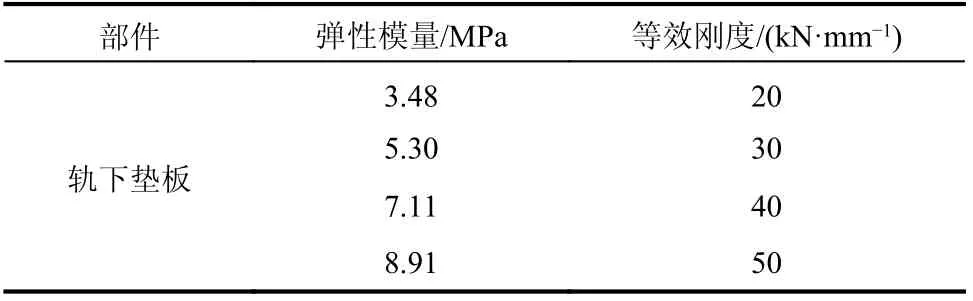
表1 軌下墊板彈性模量Table1 Elastic modulus of rail pad

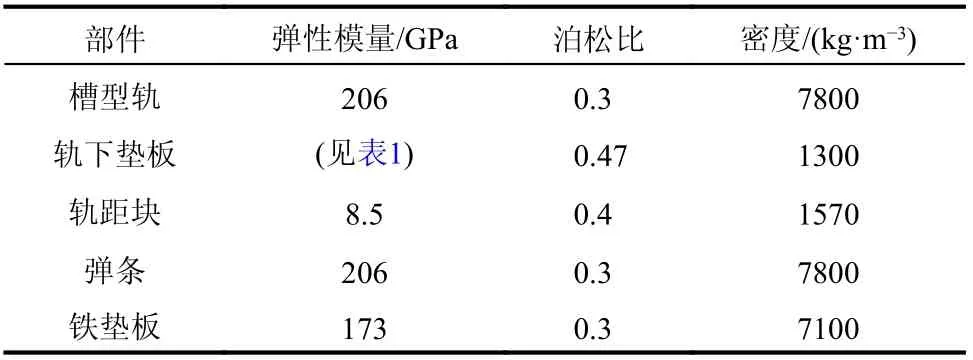
表2 材料參數Table2 Material parameters

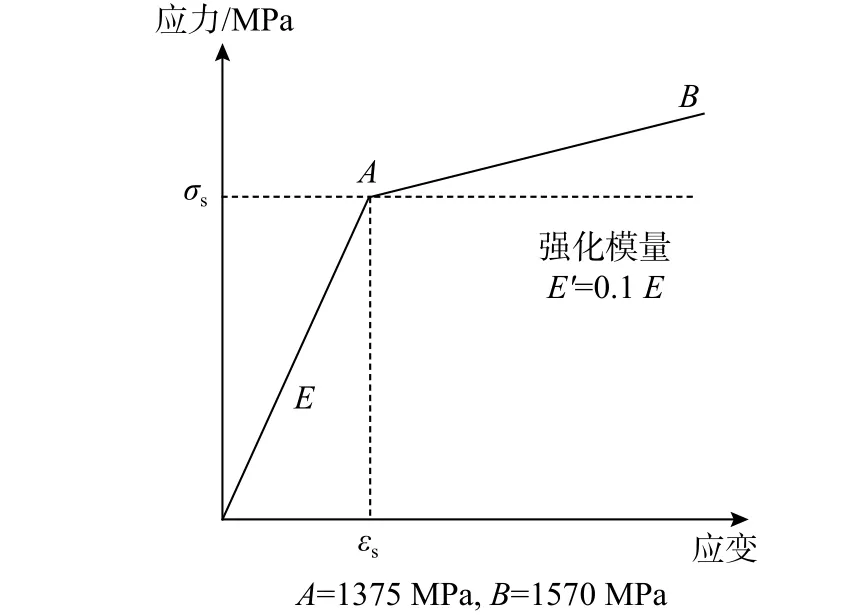
圖5 彈條材料本構模型Fig.5 The constitutive model of rail clip material

3 扣件系統模態分析

模態分析是將線性定常系統振動微分方程組中的物理坐標變換為模態坐標，使方程組解耦，成為一組以模態坐標及模態參數描述的獨立方程。

彈條在自由狀態及安裝狀態下所對應的模態固有頻率有所不同，在鋼軌-扣件系統中，考慮安裝預應力，可以更加真實地反映彈條的在不同模態固有頻率下的等效應力分布情況，按照圖6所示分析流程進行后續模態分析。

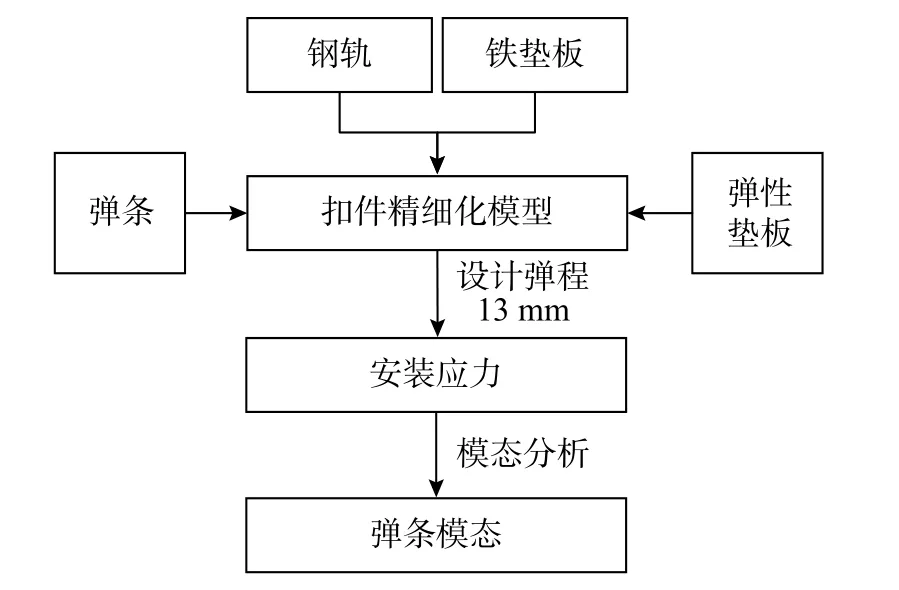
圖6 扣件系統模態分析流程Fig.6 Modal analysis of fastener system

3.1 自由狀態下彈條模態分析

對自由狀態下的彈條有限元模型進行模態分析，為了涵蓋圖3所示的典型彈條斷裂形式，對彈條前4階模態進行分析，得到相應的等效應力分布云圖如圖7所示。其中，彈條第1階和第2階模態(圖7(a)、圖7(b))使得彈條小圓弧近跟端a處等效應力較大，易發生振動疲勞斷裂，模態固有頻率分別為732.93 Hz、747.35 Hz；彈條第3階模態(圖7(c))對應小圓弧近中肢b處疲勞斷裂形式，模態固有頻率為1023.7 Hz；彈條第4階模態(圖7(d))對應大圓弧近跟端c處疲勞斷裂形式，模態固有頻率為1362.7 Hz。

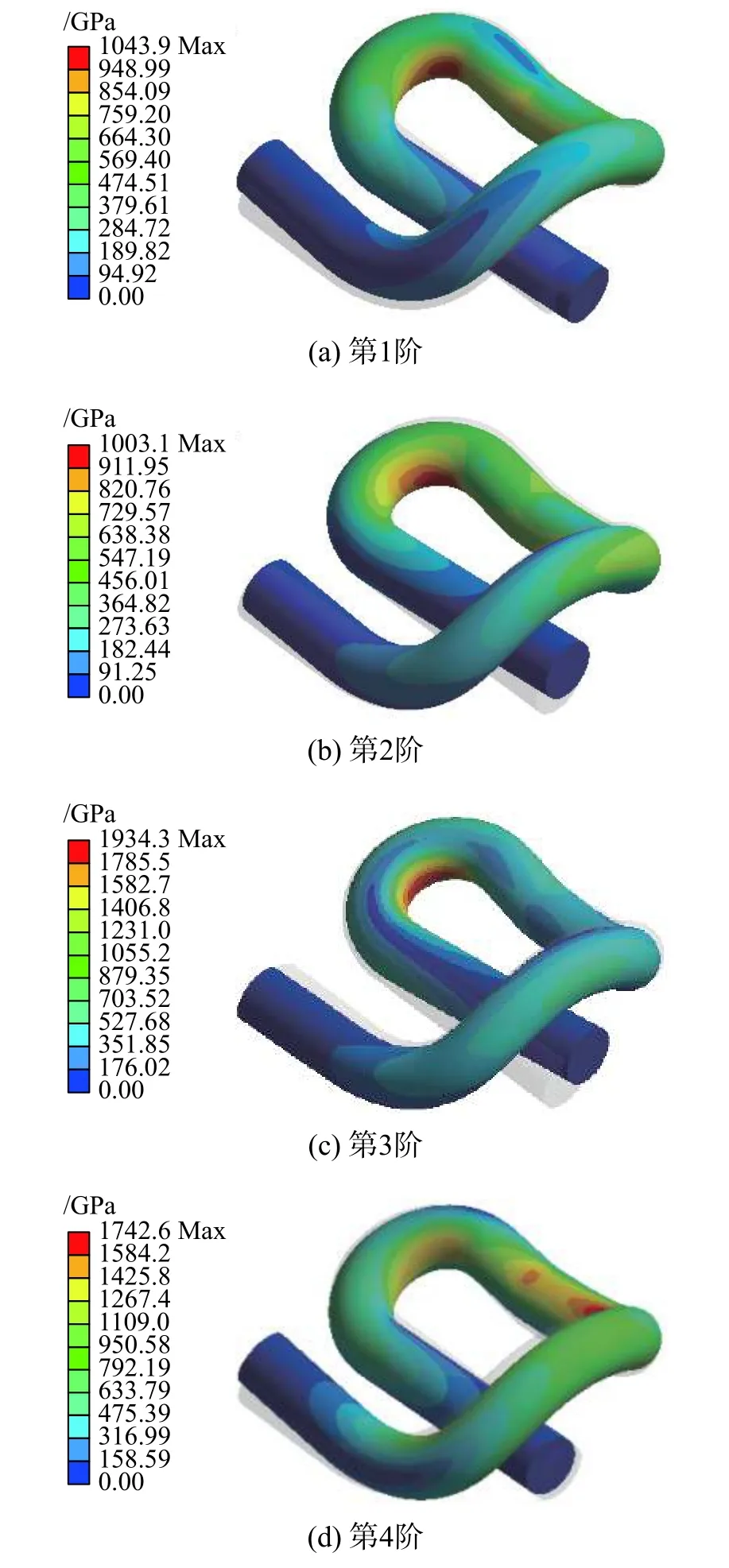
圖7 自由狀態下彈條模態振型等效應力分布Fig.7 The equivalent stress distribution of rail clip under free state

自由狀態下彈條前4階模態振型的等效應力分布可與3種典型彈條破壞形式對應，但在有軌電車線路中，波磨區段的列車通過頻率一般在1000 Hz以下，則自由狀態下彈條模態對應的固有頻率不能很好地解釋小圓弧a處及大圓弧c處的斷裂原因，仍需通過施加約束，來更加真實地反映彈條在鋼軌-扣件系統中的受力特點及模態固有頻率。

3.2 安裝狀態下彈條模態分析

在實際安裝中要求彈條小圓弧內層與鐵墊板端部的距離保持在8 mm～10 mm[13]，本文取10 mm。YGⅠ-1扣件中彈條設計彈程為13 mm，通過施加位移荷載模擬彈條安裝過程，按照圖6所示流程進行考慮安裝預應力的鋼軌-扣件系統模態分析，通過觀察對比槽型軌內外側彈條各階模態的等效應力分布情況，將典型彈條斷裂形式與彈條前20階模態對應，3種典型斷裂形式對應的彈條模態等效應力分布如圖8所示，斷裂形式與模態階數對應關系匯總結果見表3。

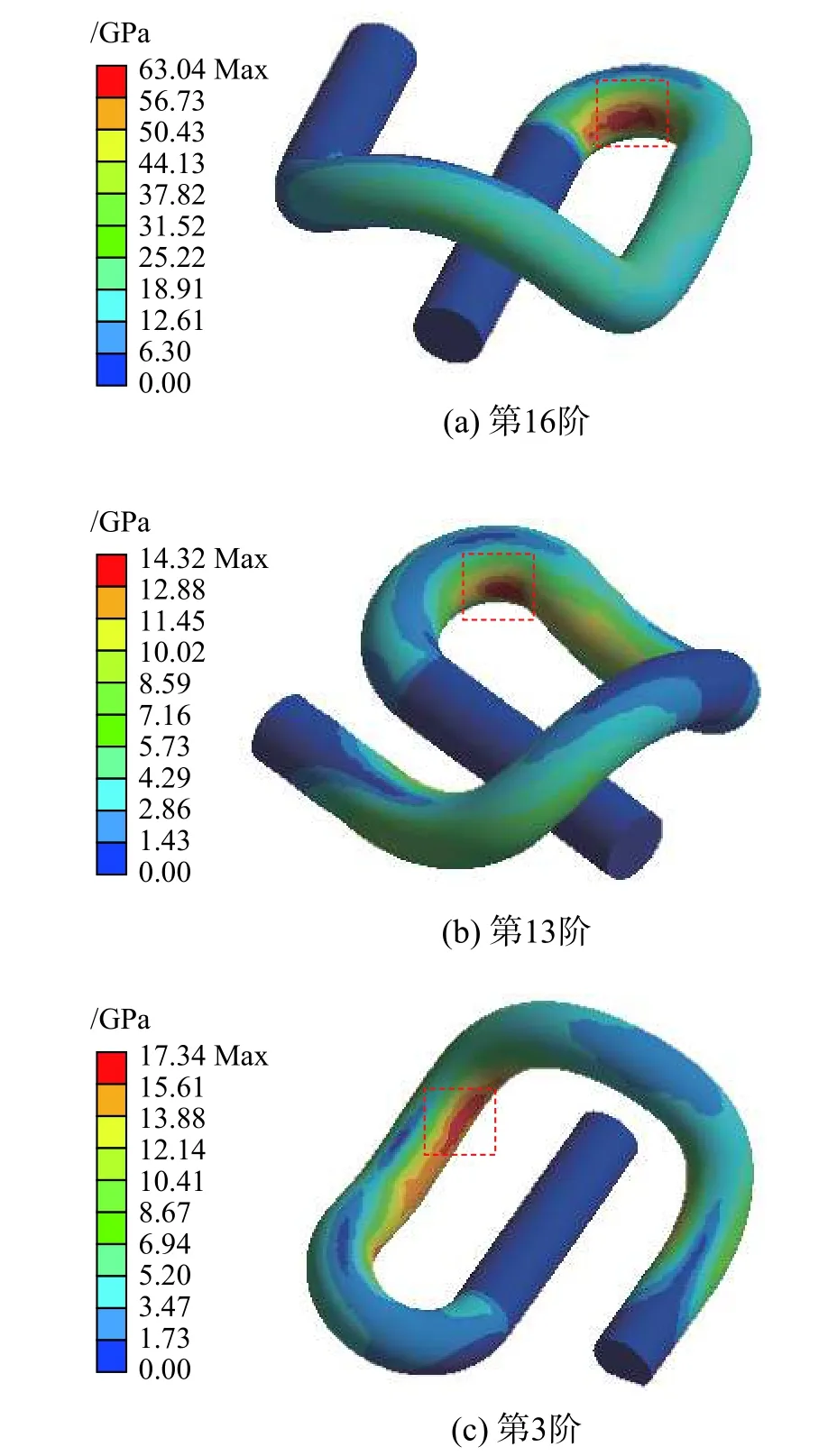
圖8 安裝狀態下彈條模態振型等效應力分布Fig.8 The equivalent stress distribution of rail clip under installation state

由表3可知，在鋼軌-扣件系統中，內、外側彈條在不同階數的模態振型下，表現出不同模態的等效應力分布情況，即同一階模態下，內、外側彈條對應不同的典型斷裂形式。小圓弧a、b處斷裂多是由10階以上模態引起的振動疲勞損傷導致，而大圓弧c處斷裂則對應10階以下模態。

表3 典型彈條斷裂形式對應模態階數結果匯總Table3 Results of mode order corresponding to typical fracture type of elastic bar

3.3 軌下墊板剛度變化對彈條模態的影響分析

扣件系統軌下墊板剛度對彈條特定階數的模態固有頻率會有一定影響，因此，對不同軌下墊板剛度下的扣件系統進行模態分析，探究不同斷裂形式對應彈條模態受軌下剛度影響的程度，是有必要的。本文取軌下墊板剛度為20 kN/mm～50 kN/mm，對應軌下墊板材料參數見表1和表2。將彈條前20階模態固有頻率與典型斷裂形式對應關系表示如圖9所示。

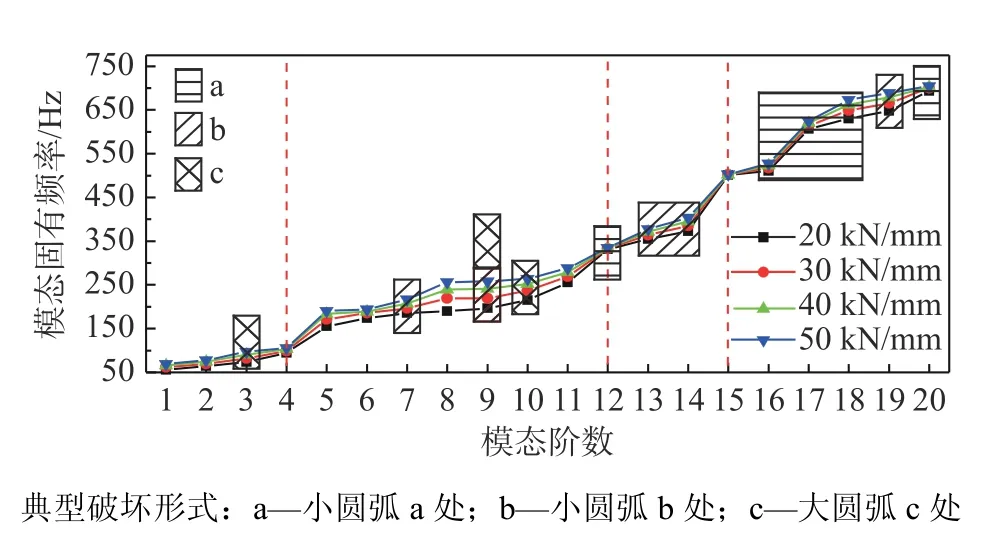
圖9 軌下墊板剛度變化對彈條模態固有頻率的影響Fig.9 Influence of the rail pad stiffness change on modal natural frequency of rail clip

由圖9可知，隨著軌下墊板剛度的增大，彈條的安裝初應力發生變化，導致彈條各階模態固有頻率都有一定程度的提高，最大提高約70 Hz。彈條第4階、12階和第15階模態固有頻率基本不受軌下墊板剛度變化的影響，而第8階～10階、18階～19階模態固有頻率則受到較大影響。

小圓弧a處斷裂形式對應彈條第12階、16階～18階和第20階模態，考慮到軌下墊板剛度變化，相應彈條模態固有頻率范圍為331.57 Hz～335.02 Hz、510.34 Hz～527.30 Hz、606.92 Hz～673.51 Hz、693.50 Hz～704.62 Hz，其中受軌下剛度影響較大的固有頻率為630.16 Hz～673.51 Hz，對應彈條第18階模態；小圓弧b處斷裂受彈條第7階、9階、13～14階和第19階模態影響，相應的彈條固有頻率為185.44 Hz～258.31 Hz、354.64 Hz～403.80 Hz、647.55 Hz～689.48 Hz，受軌下剛度影響較大的固有頻率為196.64 Hz～258.31 Hz，對應外側彈條第9階模態；小圓弧c處斷裂受彈條第3階、9階和第10階模態影響，相應彈條模態固有頻率分別為73.34 Hz～96.82 Hz和196.64 Hz～263.95 Hz，受軌下剛度影響較大固有頻率為196.64 Hz～258.31 Hz，對應內側彈條第9階模態。

因此，增加扣件系統軌下墊板剛度會提高扣件系統中彈條的模態固有頻率，彈條的3種典型破壞形式對應的模態均會受軌下墊板剛度變化的影響，在實際運營中，更換軌下墊板時，需要充分考慮墊板剛度并控制墊板剛度的變化范圍。

4 現代有軌電車通過頻率分析

扣件系統在外界列車通過時所激發的振動是引起彈條局部振動疲勞損傷的主要原因。影響列車通過頻率的因素有多種，包括軌枕間距、固定軸距、車輛定距、全軸距、鋼軌波磨等。對于現代有軌電車系統，當列車運行速度為30 km/h～70 km/h，鋼 軌 短 波 波 磨 波 長 為25 mm～80 mm時，列車通過頻率為：

式中：v為列車速度；λ為波磨波長。由式(1)計算可得列車在波磨區段的通過頻率為104.2 Hz～777.8 Hz。

4.1 列車通過頻率統計分析

按照1 km/h和1 mm的梯度離散列車運行速度及波磨波長，得到列車通過頻率與運行速度、波磨波長之間的關系，如圖10所示。由圖可知，當有軌電車以45 mm～70 km/h的速度通過波長為25 mm～40 mm的鋼軌波磨區段時，可產生500 Hz以上的高頻段列車通過頻率。

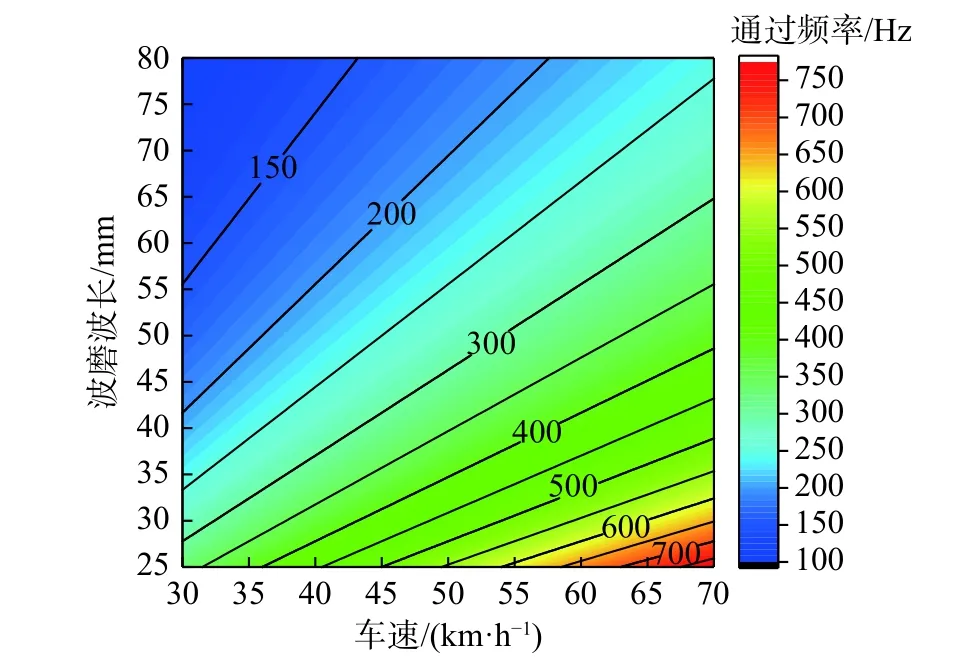
圖10 列車通過頻率與車速、波磨波長關系圖Fig.10 Relation diagram between train passing frequency,speed and rail corrugation wavelength

對列車通過頻率進行統計分析，可得其頻率分布直方圖與累計百分比如圖11所示。在各種列車運行速度及波磨波長等概率分布的條件下，列車通過頻率分布在500 Hz以下頻段的累積頻率超過90%，且在200 Hz左右頻段出現的頻率最高。考慮到有軌電車在實際運營中也是低速運行居多，列車通過波磨區段時所產生的通過頻率主要分布在中低頻段。

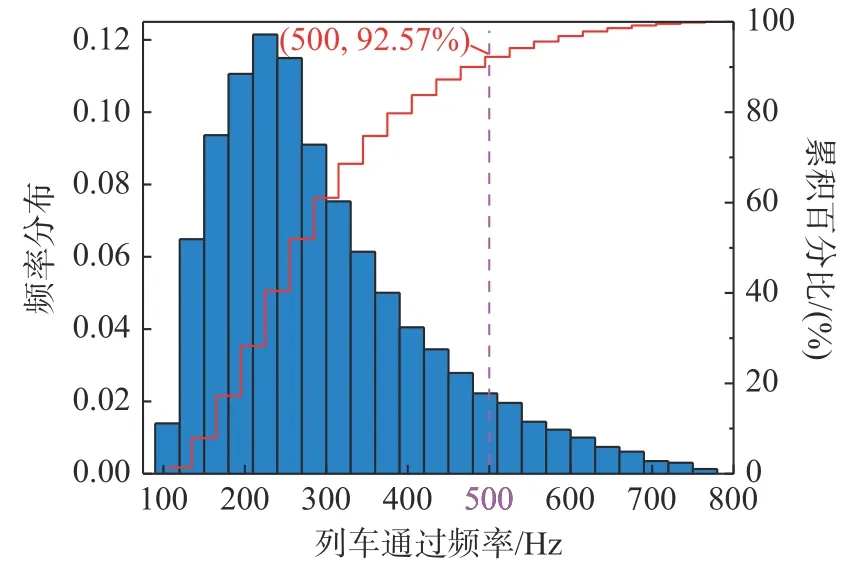
圖11 列車通過頻率直方圖及累積百分比曲線Fig.11 Histogram and cumulative percentage curve of train passing frequency

4.2 列車通過頻率與彈條模態關系分析

根據第3節結果，將各典型斷裂形式對應的彈條模態頻率以面積分布的形式建立和車速、波磨波長的對應關系，如圖12所示。

由圖12(a)～圖12(c)可知，小圓弧a處斷裂對應的彈條模態固有頻率主要分布在中高頻段，小圓弧b處斷裂對應彈條模態在中低頻及高頻段均有分布，大圓弧c處斷裂對應彈條模態則分布在中低頻，在列車車速和鋼軌波磨波長等概率分布時，3種典型彈條斷裂出現的概率分別為3.5%、36.3%和25.9%。

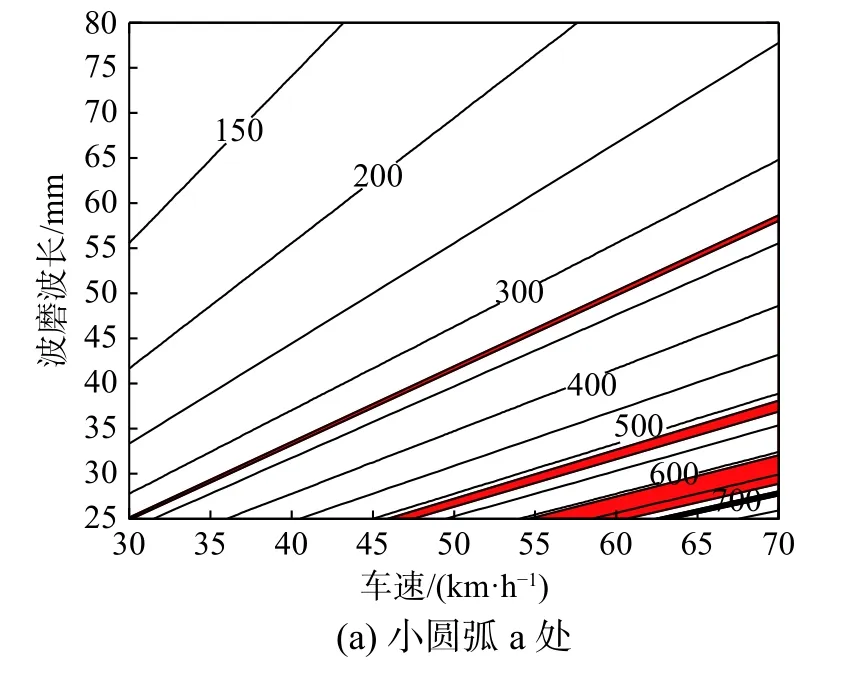
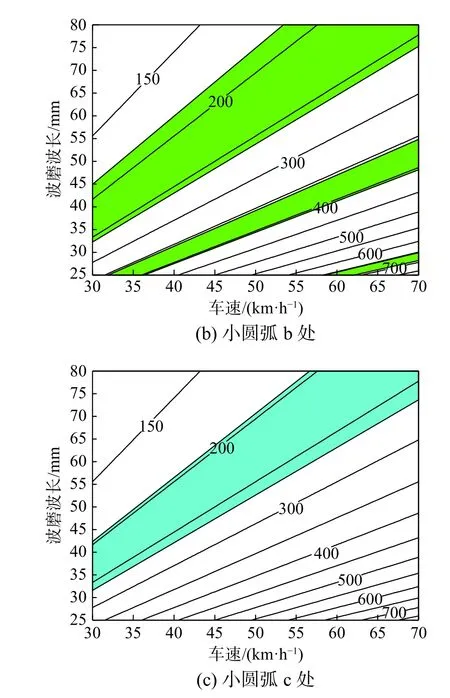
圖12 彈條模態頻率與車速、波磨波長關系圖Fig.12 Relation diagram of rail clip modal frequency with vehicle speed and rail corrugation wavelength

考慮實際有軌電車運營速度及波磨波長均分布在特定的范圍，通過對圖12的局部截取，即可獲得實際中各斷裂形式出現概率，結合脈沖激勵下鋼軌振動響應的扣件失效識別算法[17]，便于有針對性的檢測。

由圖13可得，受軌下墊板剛度影響較大的彈條模態固有頻率頻段分布于中低頻及高頻區域，其中，中低頻區域主要對應小圓弧b處及大圓弧c處彈條斷裂形式，高頻區域對應小圓弧a處彈條斷裂形式。

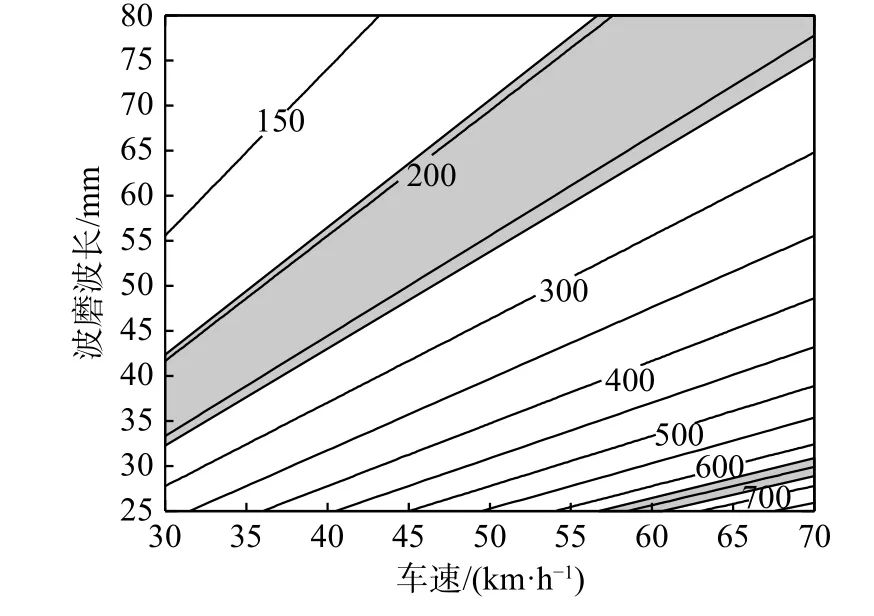
圖13 考慮軌下墊板剛度影響彈條模態頻率與車速、波磨 波長關系圖Fig.13 Relation diagram of rail clip modal frequency,vehicle speed and rail corrugation wavelength considering the influence of the rail pad stiffness

當列車通過頻率處于上述頻段時，要考慮列車速度、波磨波長及軌下墊板剛度三者的匹配關系，盡可能避開相應的敏感頻段，通過調整軌下墊板剛度、列車通過速度，實現最優的運營狀態。

5 結論

本文通過建立鋼軌-扣件系統精細化模型，對安裝預應力下的扣件系統進行模態分析，并對列車通過頻率進行分析，探究了彈條典型斷裂形式、彈條模態、列車速度、波磨波長、軌下墊板剛度之間的關系，可以得到如下結論：

(1)彈條小圓弧處斷裂與彈條中高階模態引起的振動疲勞有關，大圓弧處斷裂與彈條中低階模態引起的振動疲勞有關。對于現代有軌電車系統，列車通過頻率主要分布在500 Hz以下頻段，需要重點關注彈條小圓弧近跟端及大圓弧近跟端處彈條的傷損情況，以避免彈條斷裂的發生。

(2) 軌 下 墊 板 剛 度 在20 kN/mm～50 kN/mm范圍內變化時，隨著剛度增加，對應模態固有頻率提高，其中，受軌下墊板剛度影響較大的頻段為196.64 Hz～258.31 Hz、630.16 Hz～673.51 Hz，當列車通過頻率處于上述頻段時，需要綜合考慮軌下墊板剛度、車速、波磨波長三者的匹配關系，從而有針對性地調整軌下墊板剛度及列車運營速度，預防有軌電車扣件系統的彈條斷裂。

(3)考慮列車以30 km/h～70 km/h的速度通過波長為25 mm～80 mm的鋼軌波磨區段時，在列車車速和鋼軌波磨波長等概率分布的條件下，3種典型彈條斷裂出現的概率分別為3.5%、36.3%和25.9%。在考慮有軌電車線路實際運營條件的基礎上，可按照相同方法對指定的線路進行有彈條斷裂形式出現概率預測，從而有針對性地安排線路養護維修及傷損檢測等相關工作。