基于EM算法優化相關向量機的BDS-3超快速鐘差預報

胡 燕 王德盛 楊玉鋒

1 河南地礦職業學院測繪工程系，鄭州市永繼路51號，4514642 中國地質大學(武漢)地理與信息工程學院，武漢市錦程街68號，430076

國際GNSS監測評估系統(iGMAS)提供的超快速鐘差預報產品精度較低，一定程度上限制了北斗實時精密導航定位的應用。同時，隨著BDS-3的建成，對其超快速衛星鐘差進行精密建模和高精度預報對于維持BDS系統時間同步及滿足實時動態精密單點定位的需求等具有重要意義[1]。國內外學者提出一系列鐘差預報的模型和方法，包括譜分析模型(SA)[2]、灰色模型(GM)[2]、卡爾曼濾波及其優化模型[3]、附加周期和神經網絡補償的鐘差預報模型[4]、基于粒子群優化核極限學習機的鐘差預報算法[5]、T-S模糊神經網絡鐘差預測法[6]、小波神經網絡模型[7]及其相關的組合預報模型[8-10]等。這些模型和算法都是利用神經網絡或機器學習方法，從原始鐘差數據或基本鐘差模型擬合殘差數據出發進行模型訓練的，得到的最終鐘差預報效果雖有所提升，但仍存在一些不足：1)沒有考慮衛星鐘差數據之間的相關性，且未能充分利用鐘差數據的先驗信息；2)模型參數的選取較為困難，算法復雜度較高。針對這些問題，本文從衛星鐘差數據的相關性出發，提出一種基于EM算法優化相關向量機(relevance vector machine，RVM)的BDS衛星超快速鐘差預報算法。

1 RVM鐘差預報模型

RVM基本原理參見文獻[11]，本文不再贅述。

1.1 EM算法求解RVM模型超參數

在計算權值后驗概率過程中，部分超參數會趨于無窮大，相應的權值會趨近0，其余超參數會趨于有限值，與之對應的非零權重鐘差數據稱為相關向量，體現了鐘差數據之間的相關性。根據p(α,σ2|t)∞p(t|α,σ2)p(α)p(σ2)，RVM模型的預測問題轉變為采取有效的超參數求解方法以最大化超參數的邊緣似然函數p(t|α,σ2)問題。

(1)

式中，ω為RVM的權值向量，Ω=σ2I+ΦA-1ΦT。

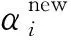
(2)

式中，γi=1-αiΣii，μi為第i個后驗權值的均值，Σii為權值后驗方差矩陣第i個對角線元素。

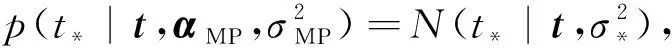
(3)

式(3)在迭代計算過程中需要進行矩陣的求逆計算，以更新模型超參數α和σ2。當鐘差訓練樣本較大時，運算量會急劇增加，同時出現奇異矩陣，無法進行求逆計算。為保證預測結果的可靠性，采用EM算法迭代更新α和σ2。基于EM迭代的RVM模型訓練算法如下：

1)對RVM模型的參數ω和σ2進行初始化。

2)根據當前ωk和(σ-2)k估計ωk+1和E(ωωT):

(4)

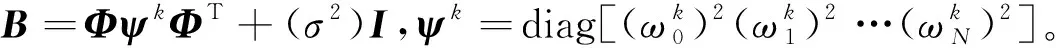
3)利用步驟2)得到的ωk+1更新方差(σ2)k+1:

(σ2)k+1=

(5)

4)判斷收斂條件‖ωk+1-ωk‖/‖ωk‖<δ是否成立，或迭代是否達到最大迭代次數。若是，則停止迭代，否則轉向步驟2)繼續新的EM迭代。

1.2 RVM模型算法超快速鐘差預報流程

基于RVM模型算法的衛星超快速鐘差預報具體流程(圖1)為：

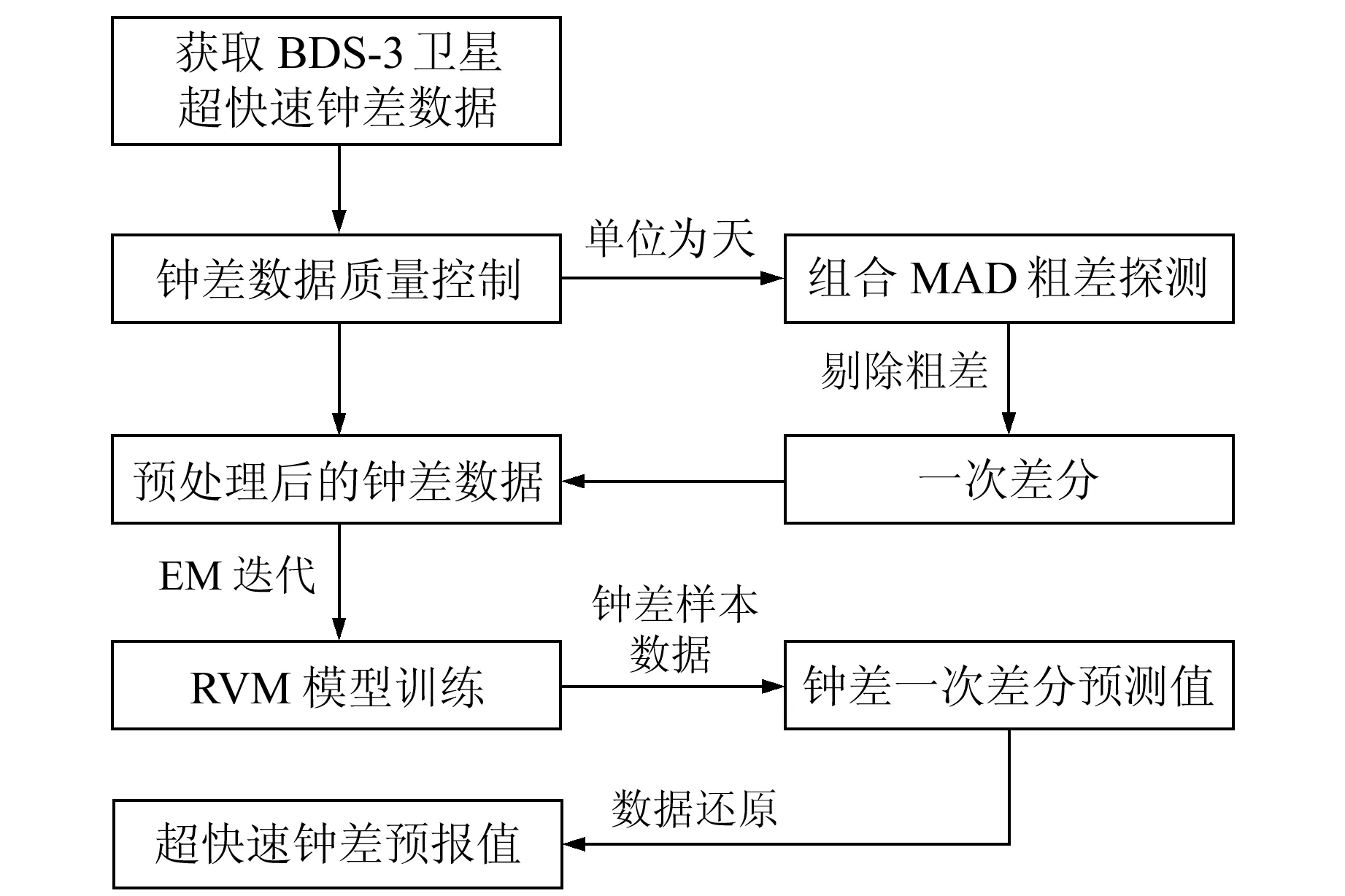
圖1 RVM模型算法超快速鐘差預報流程Fig.1 Flow chart of ultra-rapid clock offset prediction based on RVM algorithm

1)利用組合MAD法[12]預處理超快速鐘差數據，剔除粗差與鐘跳等異常值。

2)為減弱鐘差序列趨勢項的影響[7]，將鐘差數據進行一次差分處理，得到一組有效數字位數減少且數值較小的序列。

3)將鐘差一次差分數據作為RVM模型的訓練樣本，利用EM算法通過式(4)和式(5)進行迭代，求取RVM模型的超參數α和σ2，進而輸出最優的RVM預測模型。

4)給定鐘差一次差分數據樣本x*，通過優化的RVM預測模型得到樣本數據的預測值t*，最后將預報結果還原得到相應的鐘差預報值。

2 算例分析

iGMAS中心提供的超快速鐘差包括觀測部分(ISU-O)和預報部分(ISU-P)，各占24 h。ISU-O鐘差是通過對多個iGMAS中心解算的鐘差進行綜合加權得到的，精度約為1 ns；ISU-P鐘差是基于前1 d的ISU-O鐘差外推預報得到的，精度較低。本文采用iGMAS中心的實測BDS-3超快速鐘差數據，選取8顆BDS-3衛星作為代表進行鐘差預報分析，衛星信息如表1所示。

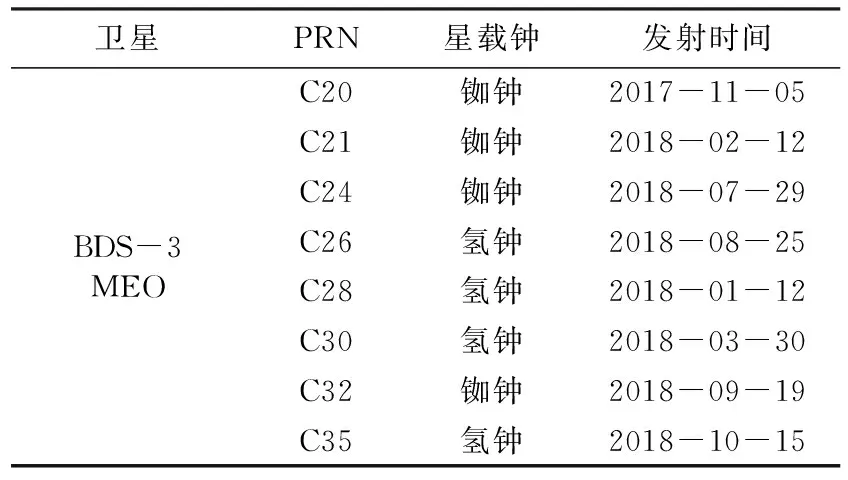
表1 BDS-3衛星相關信息

2.1 單天算例

為分析本文RVM模型鐘差預報算法的效果，采用QP模型、SA模型和ISU-P鐘差產品作為對比，其中SA模型采用加入北斗MEO衛星鐘差數據前2個主顯著周期項進行鐘差預報(主顯著周期項為12 h和6 h)[13]。選取高斯核函數作為RVM鐘差預報模型的核函數，并利用交叉驗證法進行模型訓練[11]。圖2為ISU-P鐘差產品和采用3種模型使用2021-02-13數據預報2021-02-14鐘差的預報殘差。

從圖2可以看出：1)ISU-P鐘差產品隨著預報時間的推移累積預報誤差很大，預報精度衰減很快，精度有待進一步提高；2)QP模型與SA模型的鐘差預報精度略優于ISU-P鐘差產品，兩者預報結果差別不大；3)SA模型加入了鐘差數據的前2個主周期項，改善了部分衛星鐘差在預報過程中周期性系統誤差的積累，發散程度有所減小，但提升效果并不明顯，由此可見BDS-3衛星鐘差數據的周期特性誤差并不顯著；4)RVM模型的預報精度最高，誤差曲線最收斂，超快速鐘差預報穩定性更好。綜上，EM算法優化的RVM鐘差預報模型可更為準確地擬合出鐘差數據中的非線性特征，從而取得較好的超快速鐘差預報效果。

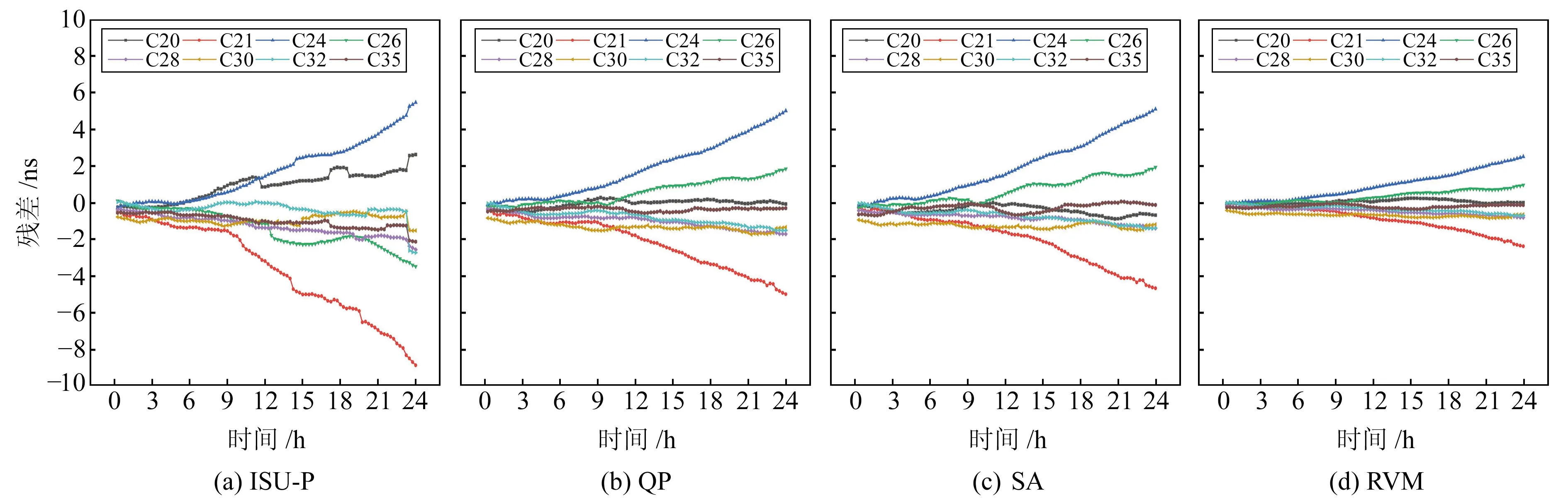
圖2 不同預報模型BDS-3衛星鐘差預報殘差序列Fig.2 Clock offset prediction residual sequence of BDS-3 satellites using different prediction models

2.2 多天算例

為更好地驗證本文RVM模型進行鐘差預報的普適性，采用2021-02-13～19共7 d的BDS-3超快速鐘差數據進行實驗分析，選取均方根誤差(RMS)作為鐘差預報精度的評定標準，預報結果如表2和圖3所示。

由表2和圖3可以看出：1)隨著預報時長的增加，4種預報模型的超快速鐘差預報精度都有所下降，但ISU-P產品精度下降最快，降低幅度最為顯著，可見當前階段超快速鐘差預報產品精度很低，難以滿足實時精密單點定位的需求；2)QP模型與SA模型的鐘差預報精度相當；3)RVM模型預報精度與穩定性均優于其他3種預報模型；4)在短期6 h超快速鐘差預報下，RVM模型BDS-3鐘差預報精度優于0.62 ns，能夠滿足北斗高精度實時PNT服務。

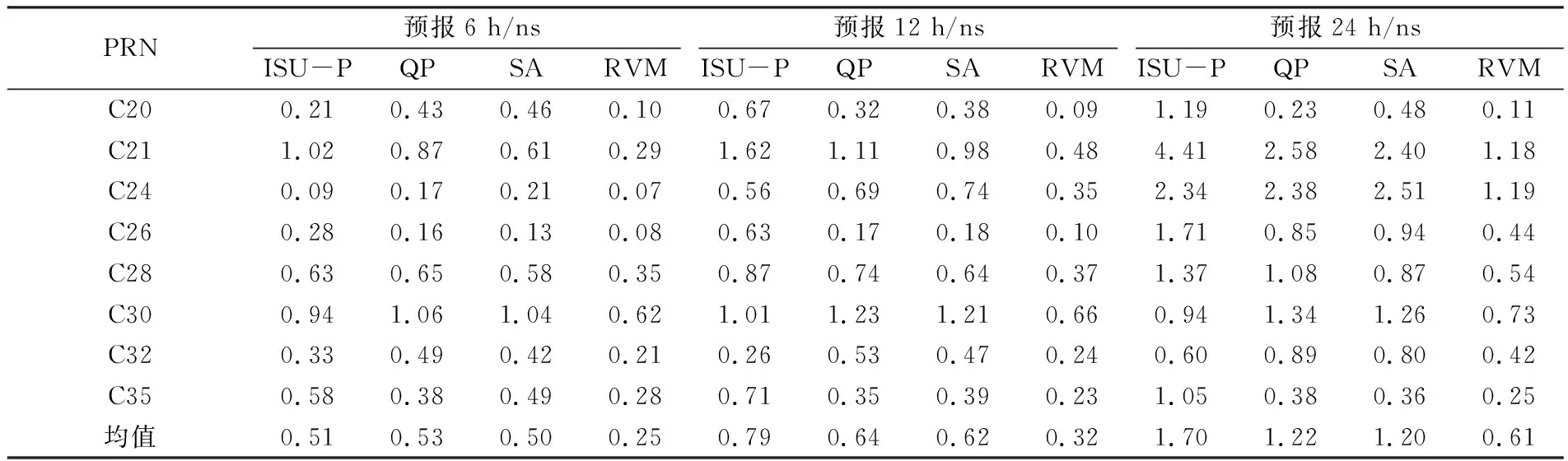
表2 不同預報模型一周預報結果平均精度統計

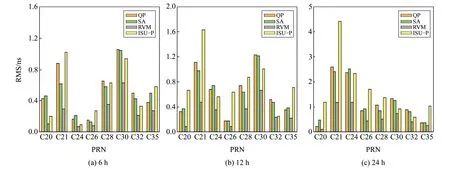
圖3 不同預報模型BDS-3衛星鐘差預報精度統計Fig.3 Statistics of BDS-3 satellites clock offset prediction accuracy using different prediction models

為了分析BDS-3衛星鐘差的預報效果與星載鐘類型的關系，表3統計了不同星載鐘類型鐘差數據預報的平均精度。表4給出了RVM模型較其他3種模型預報精度的提升率。

表3 不同星載鐘類型鐘差預報的平均精度

表4 RVM模型較其他3種模型精度提升率

由表3～4可以看出：1)在進行12 h鐘差預報時，BDS-3衛星銣鐘和氫鐘的鐘差預報精度相當，但在預報24 h鐘差數據時，BDS-3衛星氫鐘的預報精度明顯更優，可見BDS-3搭載的新一代氫鐘穩定性更強，性能優于同期的銣鐘。2)對于6 h、12h和24h預報，RVM模型預報BDS-3衛星鐘差數據的平均精度均優于0.61 ns；與ISU-P、QP模型和SA模型相比，RVM模型預報24 h的BDS-3衛星鐘差精度分別提升64.1%、50.0%和49.2%，驗證了RVM模型在BDS-3超快速鐘差預報中的可行性。

3 結 語

針對當前BDS-3鐘差預報產品無法滿足實時高精度PNT服務需求的問題，提出一種基于EM算法優化RVM的BDS-3超快速鐘差預報算法。利用iGMAS中心提供的實測BDS-3超快速鐘差數據進行單天和多天預報實驗，驗證RVM模型在衛星鐘差預報中的可行性，同時得出以下結論：

1)BDS-3超快速鐘差數據進行一次差分后，數據的有效數字位數減少，一定程度上消除了鐘差序列趨勢項的影響，有利于更準確地擬合預測模型。

2)RVM模型采用高斯核函數，具有較強的局部學習與全局泛化能力，能夠很好地對超快速鐘差數據進行刻畫。

3)對比4種模型24 h鐘差預報的誤差曲線發現，RVM模型精度最高，誤差曲線最收斂，穩定性最好。可見EM算法優化的RVM鐘差預報模型可更準確地擬合鐘差數據中的非線性特征，從而取得較好的超快速鐘差預報效果。

4)對于6 h、12 h和24 h預報，RVM模型預報BDS-3衛星鐘差數據的平均精度均優于0.61 ns；與ISU-P、QP模型和SA模型相比，RVM模型預報24 h 的BDS-3衛星鐘差精度分別提升了64.1%、50.0%、49.2%。

致謝：感謝iGMAS數據中心提供產品支持。