基于偏差改正的病態模型Liu估計的單位權方差無偏估計

丁斌芬 安潔玉

1 江西應用科技學院軟件與區塊鏈學院，南昌市聯福大道1號，330100

當觀測模型的系數陣呈良態時，最小二乘法能獲得最優無偏的參數估值。然而，當模型的系數陣呈病態時，微小的觀測誤差會導致解的巨大波動，使常規最小二乘估計的解不可靠[1]。為此，學者們提出多種估計方法，如 Tikhonov 正則化、嶺估計、截斷奇異值分解(truncated singular value decomposition，TSVD)和Liu估計等[2-9]。目前關于病態模型的有偏性研究大都集中于Tikhonov正則化或TSVD 正則化[10-12]，鮮有涉及Liu估計的相關研究。不同于Tikhonov 正則化，Liu 估計除含有正則化參數外，還額外引入了一個修正因子，因此可更加靈活地處理病態問題[7-9]。但由于引入了正則化參數和修正因子，Liu估計是有偏的。事實上，Liu估計正是通過犧牲參數估值的無偏性來換取其有效性。

基于以上研究，本文首先分析了由于引進正則化參數和修正因子而導致的Liu估計解及其殘差的偏差；然后將偏差從殘差中扣除，并利用偏差改正后的殘差導出Liu估計的單位權方差估計公式；最后用數值算例和病態測邊網算例驗證公式的有效性。

1 病態模型及其Liu估計解法

測量上常用的Gauss-Markov模型為：

y=Ax+e

(1)

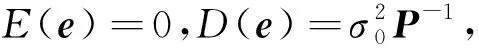
(2)

式中，N=ATA。當系數矩陣病態時，最小二乘解變得極不可靠。Liu[7]采用Liu估計解算病態模型參數，其在最小二乘準則的基礎上額外增加了一個約束項，即

eTe+fTf=min

(3)

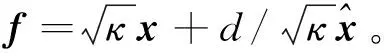
(4)

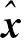
2 基于偏差改正的Liu估計的單位權方差估計

2.1 Liu估計的殘差及其偏差

(5)

將式(5)代入式(1)中可得殘差：

(6)

對式(6)兩邊取期望，得：

(7)

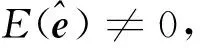
(8)

將式(8)代入式(1)，可得殘差為：

(9)

對式(9)取期望可得殘差的偏差：

(10)

2.2 基于偏差改正的單位權方差估計

傳統基于殘差計算單位權方差的公式為：

(11)

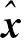
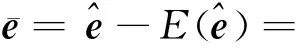
(12)

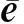
(13)

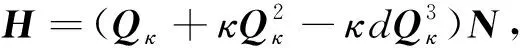
(14)

則方差陣的跡為：

(15)

由二次型的數學期望公式有：

(16)

(17)

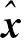
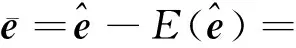
(18)

其方差為：

(19)

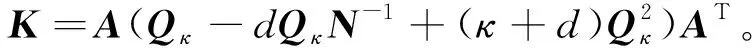
(20)

式中，

(21)

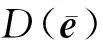
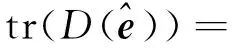
(22)

顧及式(16)可得單位權方差：

(23)

3 算例與分析

3.1 數值算例

Hilbert矩陣是一類典型的病態矩陣，假設A∈Rm×n為某一Hilbert矩陣，其元素構成為：

(24)

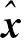
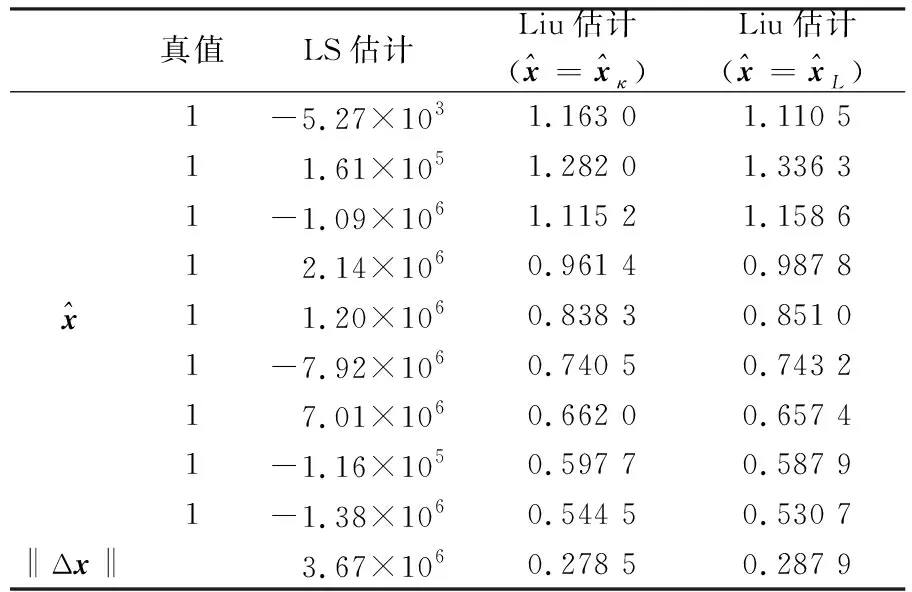
表1 σ0=0.1時不同算法解算的參數估值

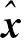
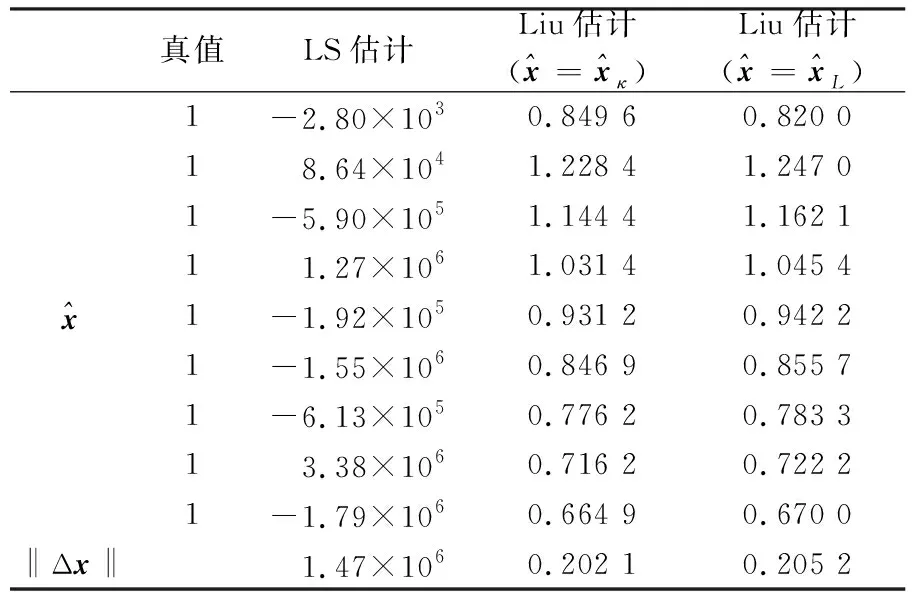
表2 σ0=0.01時不同算法解算的參數估值

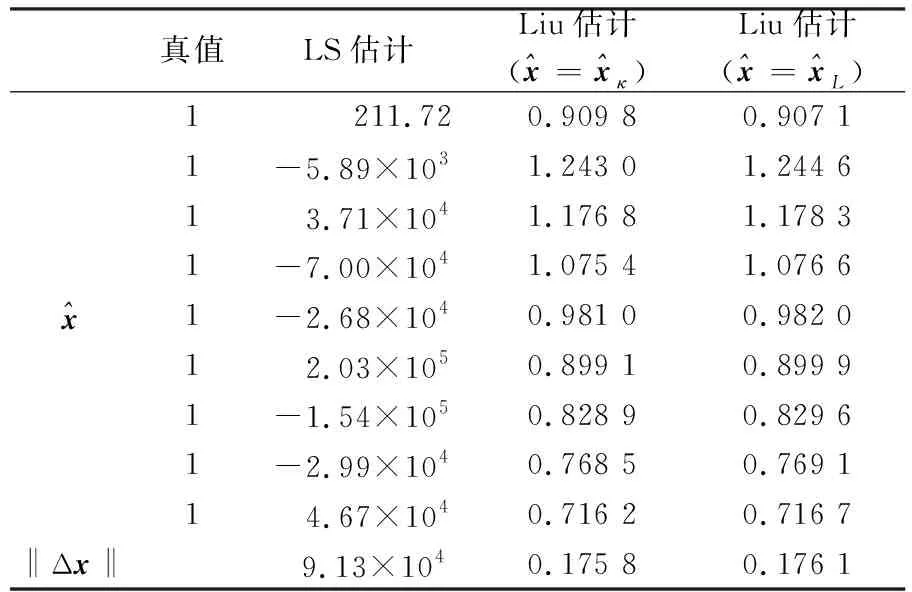
表3 σ0=0.001時不同算法解算的參數估值

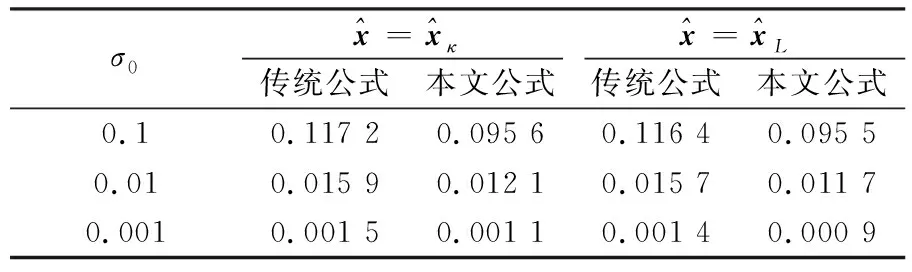
表4 本文公式和傳統公式估計的單位權方差

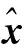
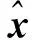
圖1 500次實驗2種方法估計的單位權方差Fig.1 The unit weight variance estimated by two approaches for 500 experiments

3.2 病態測邊網算例

為進一步驗證本文公式的有效性，模擬一個病態測邊網。圖2為網的點位平面分布，其中共有11個點位，包括9個已知點P1～P9和2個未知點P10、P11，P10和P11的真實坐標分別為(0,0,0)和(7,10,-5)。表5為P10、P11坐標及其到已知點的距離觀測值，各觀測值的精度均為5 mm。現要求利用這些距離觀測值求解未知點的坐標。本算例中，由于測邊網的幾何構型較差，其觀測方程的法矩陣條件數為4.585 1×103，存在病態。

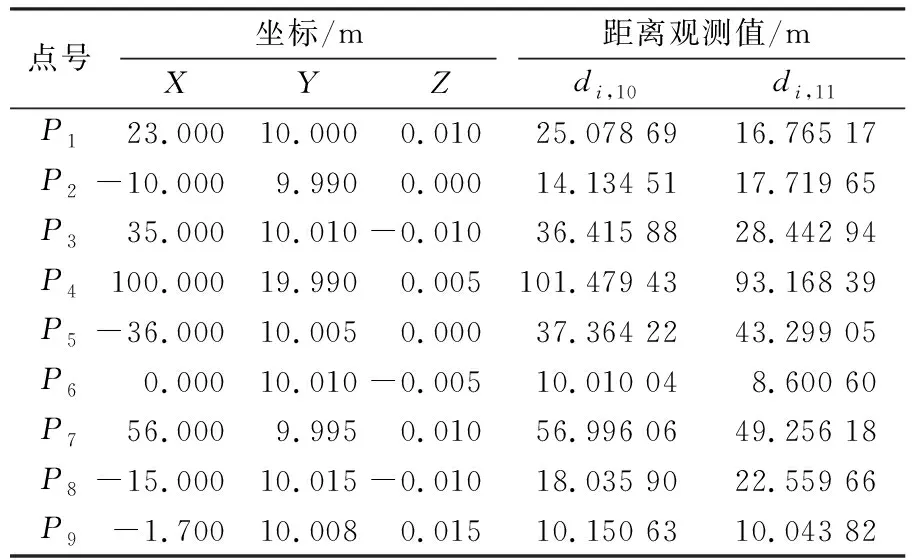
表5 控制點的坐標及距離觀測值

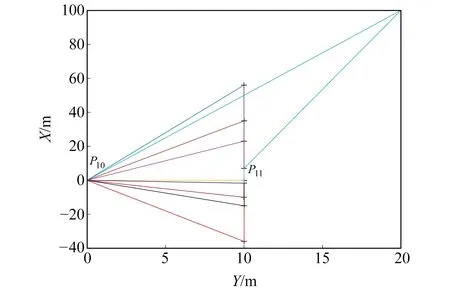
圖2 空間測邊網的點位平面分布Fig.2 The distribution of the points of the space net in XY plane

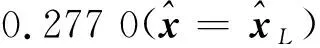
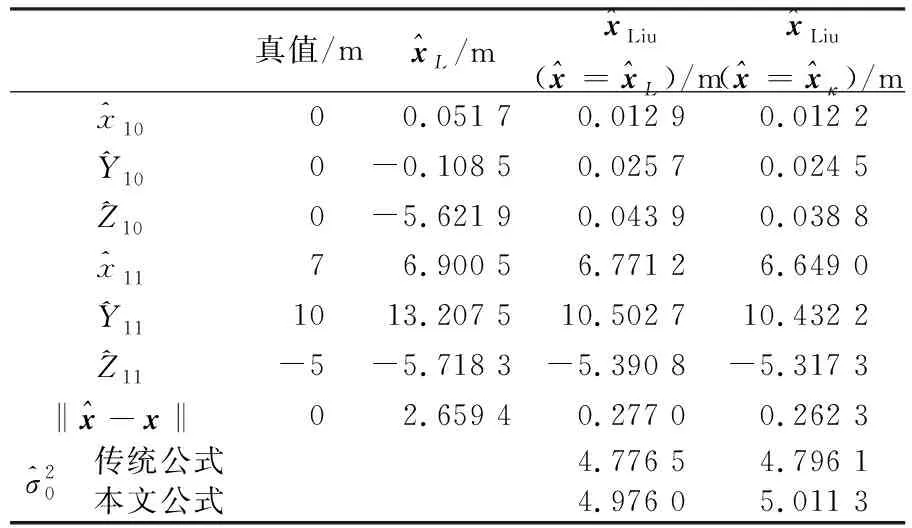
表6 不同算法解算的參數估值及與真值的差值范數

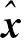
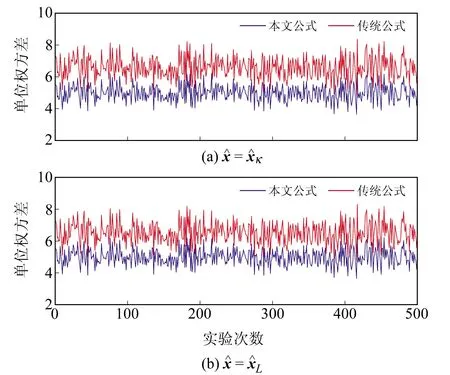
圖3 500次實驗2種方法估計的單位權方差Fig.3 The unit weight variance estimated by two approaches for 500 experiments

4 結 語

Liu 估計是病態模型的常用解法之一，其通過引入正則化參數和修正因子有效地削弱了系數陣小奇異值對參數估值及其方差的放大，但同時也引進了偏差，進一步導致其殘差也是有偏的。本文首先計算了Liu估計殘差的偏差，并將其從殘差中剔除，得到偏差改正后的殘差；然后基于向量二次型的數學期望公式，利用改正后的殘差導出Liu估計的單位權方差估計公式；最后設計2個算例對本文公式進行驗證。結果表明，殘差中的偏差會嚴重影響單位權方差的估計，在將偏差從殘差中扣除后，利用改正后的殘差估計的單位權方差更符合實際情形。