非正交剛性角反射器聲散射特性研究?

謝濤濤 羅 祎 程錦房 肖大為

（海軍工程大學兵器工程學院 武漢 430033）

1 引言

角反射器由于結構特性，可使入射波在內部多次反射后，沿入射方向反射回去［1］，因此角反射器被廣泛的應用于電磁學和聲學領域。在聲學領域中，角反射器作為一種無源聲對抗裝置［2］，常用于標記水下重要設施如海底電纜、石油管道等；在軍事應用上，基于其聲散射特性，可將角反射器作為假目標來模擬水下艦船、圓柱殼體等水下反聲目標以對抗聲納探測，也常與主動聲源結合來模擬大尺度水下聲學目標［2］。因此角反射器的聲散射特性研究具有較為重要的民事、軍事意義。

國內對于水下板殼結構的聲散射特性研究主要基于邊界元、有限元等仿真軟件，例如：孫鐵林等對水下彈性板殼的聲散射特性進行研究［3］；吳學峰等使用有限元法及邊界元法對板式結構的聲輻射特性進行分析［4］；魏克難等使用耦合邊界元法對水下目標的低頻散射特性進行研究分析［5］；馬建利用邊界元法對剛性圓柱聲散射進行研究分析［6］等。上述研究大多針對特定形狀或材料的聲學特性，但是在還未有針對水下角反射器的非正交特性的相關研究。

常見的角反射器有二面角反射器與三面角反射器，構成角反射器的金屬板相互垂直，也將其稱為正交角反射器。實際加工裝配中難以滿足板間相互垂直的條件，因此需要研究非正交角反射器的聲散射特性，分析加工誤差導致的金屬板間不垂直對目標強度值與散射寬度的影響。

2 基本理論

邊界元（Boundary Element Method，BEM），又稱邊界積分方程方法（Boundary Integral Equation Method）是將問題的微分方程變成邊界上的積分方程，然后引入邊界上的有限個單元將積分方程離散，得到只含有邊界上節點未知量的方程組，然后進行數值求解［7］。

SYSNOISE邊界元仿真軟件可分為直接邊界元法與間接邊界元法，SYSNOISE認為間接邊界元法模型內外部都有流體介質的存在，而直接邊界元法只能在邊界元的一側存在［8］。當研究對象為無限水域中的角反射器，且模型內部無流體時，選擇直接邊界元法進行仿真分析，并默認結構與流體邊界為剛性邊界［9］。

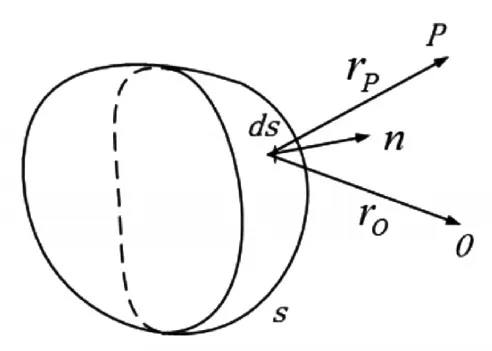
圖1 邊界元法幾何關系

定義物體處于無限理想流體介質中，S為物體外表面，n為Q的外法線單位矢量，O為入射聲源，P為空間中的點。P點散射聲場的Helmholtz積分解可表示為

3 仿真和分析結果

ANSYA作為建模分析軟件，具有較強的前處理功能［10］，使用ANSYS進行模型構建及網格劃分。SYSNOISE作為較為完善的聲學分析軟件，具有較強的聲學后處理功能，可根據入射條件求得空間中任意一點處的聲學量，即聲壓、聲強、聲功率等，但其自身前處理功能較差，不具備獨立建模的功能，因此需要使用其數據接口進行外部模型導入。

由于求解模型厚度較小，在ANSYS中將模型定義為殼體單元（shell 181），分別建立二面及三面角反射器模型，材料為鋼［11］（密度為7800kg/m，泊松比為0.3，彈性模量為2.1E11）。設聲源為平面波，距離目標聲學中心（坐標x、y、z=0）100m，入射方向為聲源中心方向，入射波頻率為5kHz～15kHz，幅值為1Pa，入射波角度以三度為一個單元，從0°入射至90°。根據網格劃分要求即最短的波長內至少含有6個單元［12］，最小波長為0.1m，則網格不得大于0.016m，考慮到網格數量太大會使計算效率極大降低，因此角反射器邊長定義為0.5m，最大限度地減小計算量，提高運算效率。

3.1 非正交二面角反射器的聲散射特性分析

二面角反射器由于：1）結構簡單、易于加工生產且成本較低；2）方向朔回特性，可將入射信號最大程度的反射。因此在水聲學領域中，常將其作為障礙物標定器，放置于水上/水下浮標上。

因為實際加工生產裝配中會產生誤差，因此對板間夾角的變化與入射角度之間的關系進行分析，研究板間夾角對目標強度值、散射寬度的影響，以及入射波頻率與平板間夾角的關系等。

如圖2所示，取二面角反射器邊長l為0.5m，γ為板間夾角（本節γ=90°，85°，80°），依次定義這三個角度對應的角反射器為A2、B2、C2；θ為垂直方向上的入射角度，本節取為θ=90°，φ為水平方向上的入射角度，也是本文研究的重點，目標強度值隨入射角φ值改（0°～90°）變而發生的變化為本節主要研究內容，具體分析如圖3～5所示。

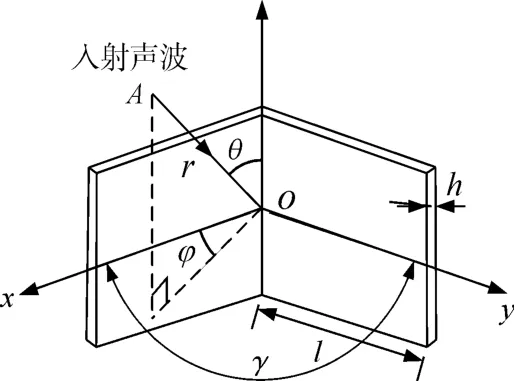
圖2 二面角反射器

由圖3～5可知，二面角反射器目標強度值隨入射角度變化曲線沿45°入射方向對稱，目標強度值隨聲波頻率增大而增大，非正交角反射器B2、C2總體目標強度值要小于正交角反射器A2，由于特征曲線的對稱性，對入射角0°～45°范圍內進行分析可得以下結論：

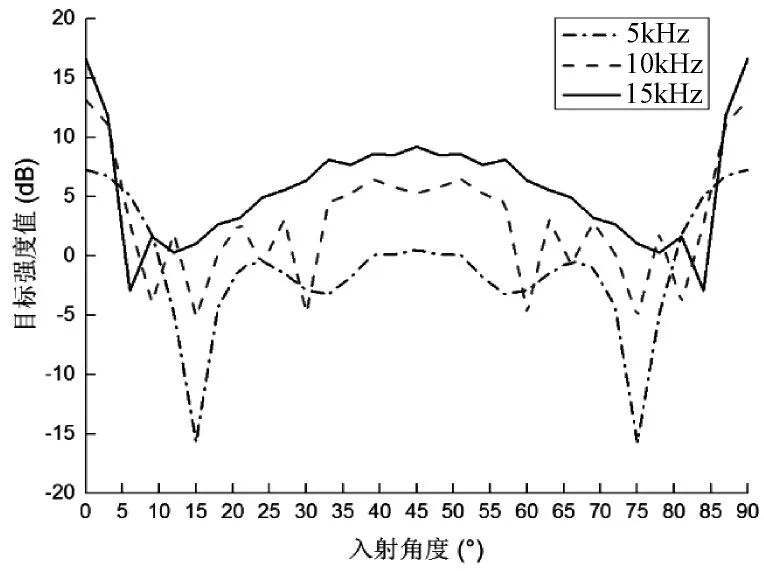
圖3 90°二面角反射器目標強度值

1）二面角反射器的目標強度值隨入射角度改變波動明顯，A2、B2、C2曲線在0°處出現第一個波峰即極大值，在45°時出現第二波峰；

2）正交二面角反射器基本可滿足隨入射波頻率增加，目標強度值相應的也增加。非正交角反射器B2的曲線波動性較大，穩定性較差，C2無法滿足該規律，相反低頻入射聲波具有較強的目標強度值；

3）二面角反射器極小值出現在5°～15°之間。其中入射波頻率為15kHz時極小值出現在入射角為5°附近；入射波頻率為10kHz時，極小值的位置隨板間夾角γ的變化而發生改變，但基本都出現在10°以內；入射波頻率為5kHz時，極小值出現在10°～15°之內，較為穩定；

4）正交角反射器在0°及90°時取得極大值為16.58dB，但是出現后又急劇減小。在45°時目標強度值為9.439dB，且在35°～55°時波動較小，散射寬度較大；

5）非正交角反射器B2散射寬度較大，但目標強度值較小；C2目標強度與散射寬度最小。

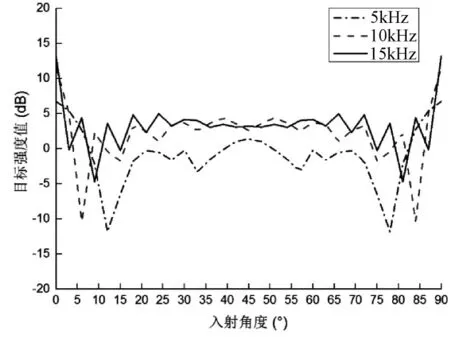
圖4 85°二面角反射器目標強度值

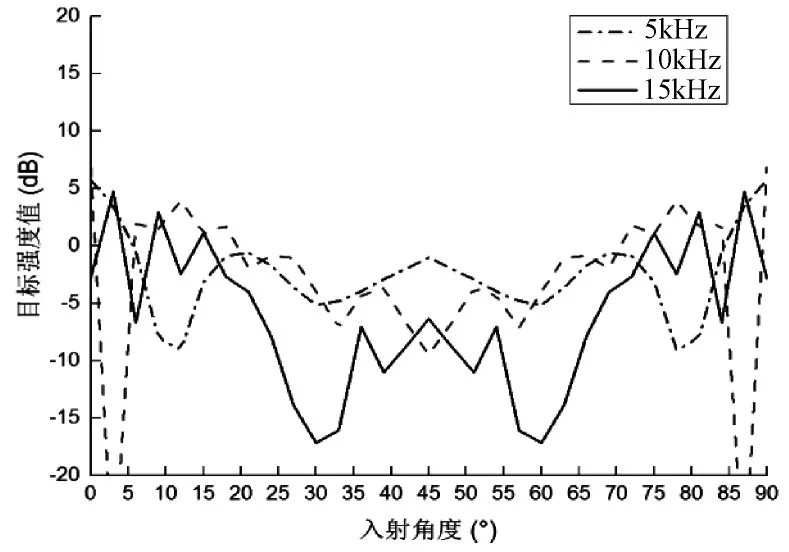
圖5 80°二面角反射器目標強度值

當入射聲波頻率為15kHz時，將該條件下三個角反射器目標強度值隨聲波入射角度改變的特征曲線進行對比（如圖6所示），可得如下結論：

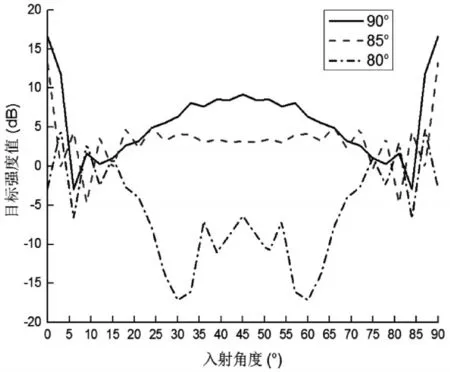
圖6 二面角反射器目標強度曲線（頻率15kHz）

1）A2、B2、C2分 別 在 入 射 角 0°取 得 最 大 值（16.58dB、13.19dB、-2.799dB）；

2）正交二面角反射器A2散射寬度較大，即最大目標強度值附近波動小，目標強度值在入射角度35°～55°范圍內目標強度值差異較小，滿足較大角度范圍入射下，目標回波強度保持在一個穩定的值。非正交角反射器B2方向性也較好，但強度低于A2；而C2目標強度值隨角度變化波動明顯，散射寬度較小，聲散射特性較差。

圖7為二面角反射器A2的表面聲壓云紋圖，可以看出，二面角反射器在不同頻率下，聲壓成帶狀分布均勻，入射頻率影響聲壓帶寬度，入射頻率越高帶寬越窄，且聲壓帶平行分布，證明了二面角反射器方向朔回性較強。

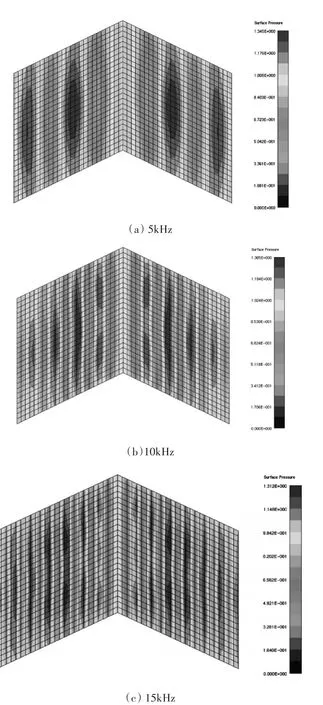
圖7 二面角反射器不同入射波頻率下聲壓云紋圖

3.2 非正交三面角反射器聲散射特性

三面角反射器也稱為三棱型反射器（如圖8所示），由三個面構成，常用于水面假目標模擬或障礙物標定。當三個金屬板相互垂直時則為正交三面角反射器；當三個金屬板相互間不垂直時，為非正交角反射器。本節主要研究正交三面角反射器與板間夾角為85°、80°時的聲散射特性。

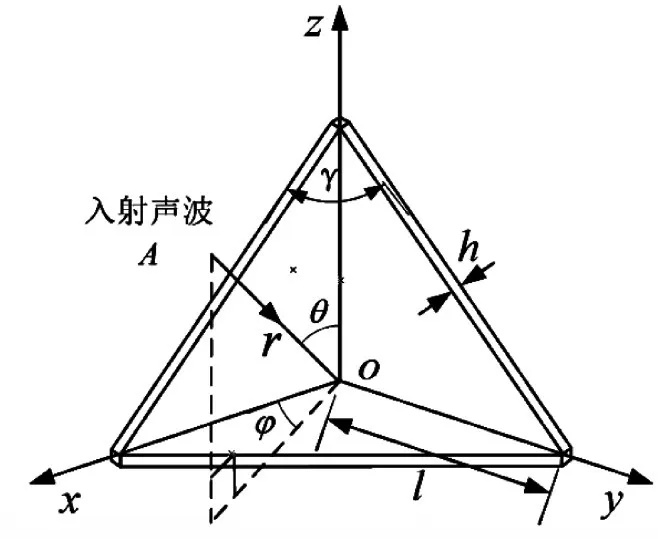
圖8 三面角反射器

如圖8所示，取三面角反射器邊長l為0.5m，本節中分別取γ=90°、85°、80°（這三個角度對應的反射器依次命名為A3、B3、C3），本節θ=90°。具體分析見圖10～12。

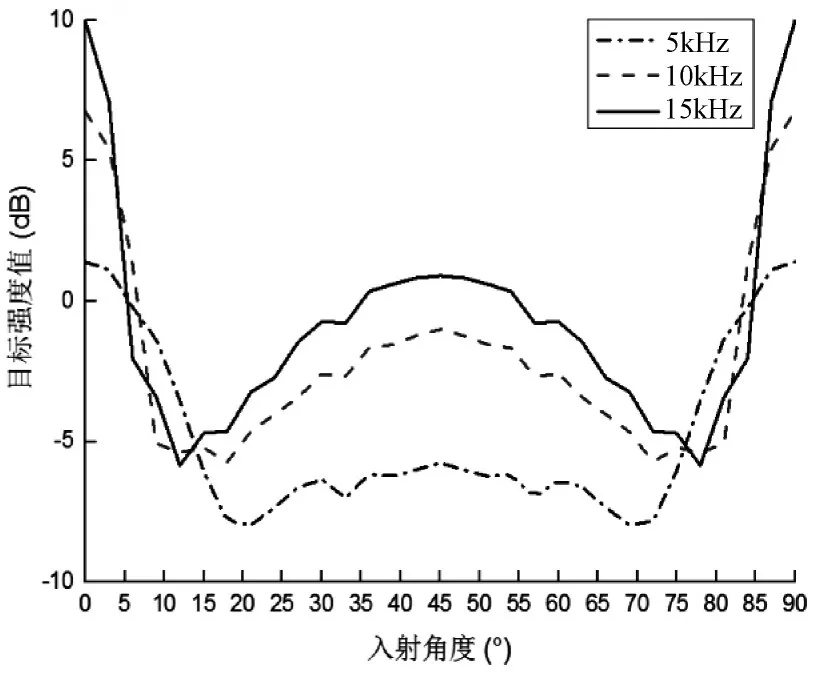
圖9 90°三面角反射器目標強度值

由圖10～12可知，在相同的入射條件下，隨著平板間夾角γ的改變，正交角反射器與非正交角反射器的目標強度值隨入射角度改變的特征曲線也是沿45°入射角對稱，且有如下特征。

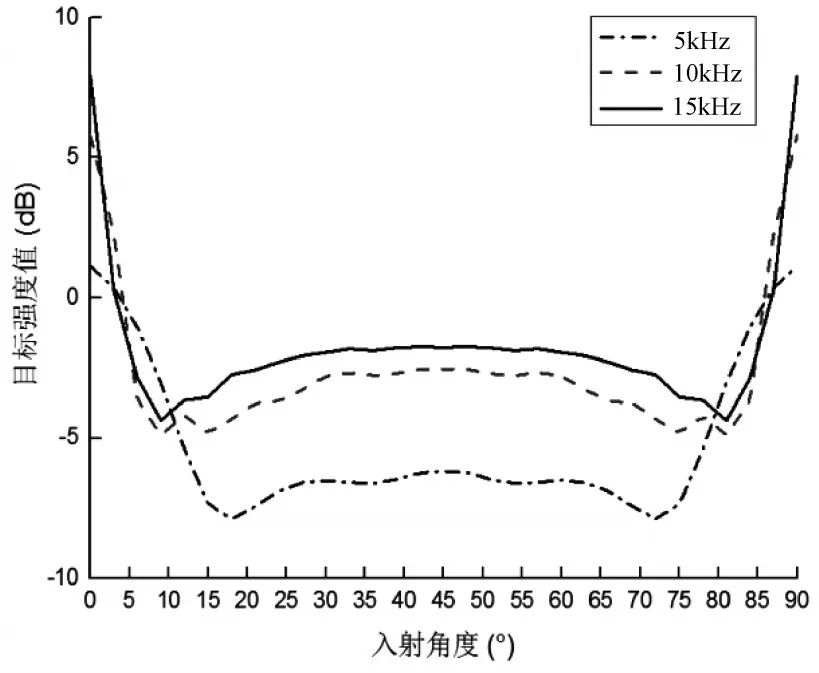
圖10 85°三面角反射器目標強度值

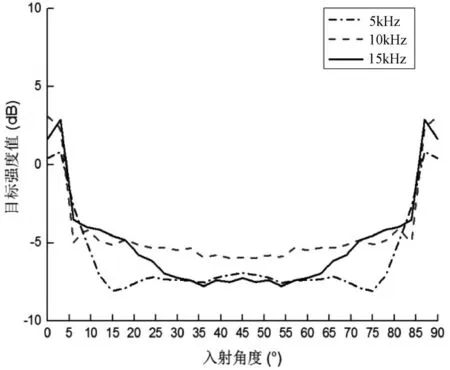
圖11 80°三面角反射器目標強度值

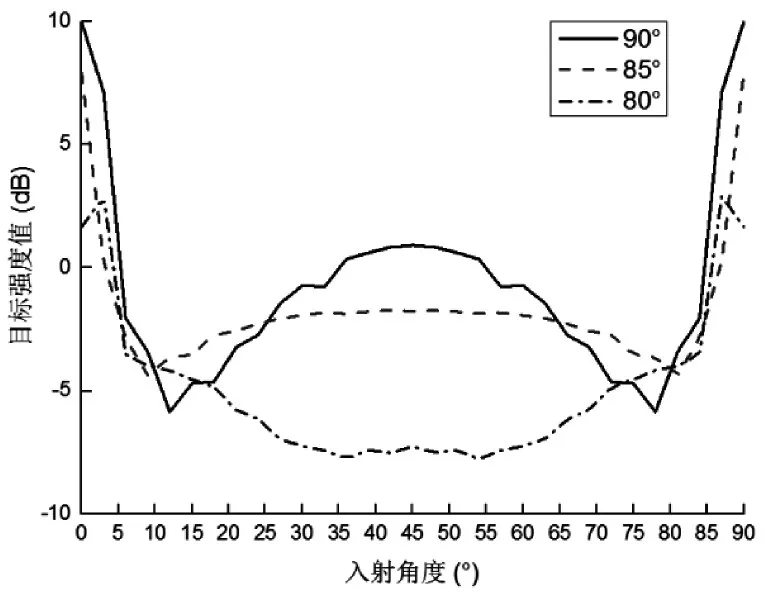
圖12 15KHz下三面角反射器目標強度曲線

1）聲源相同的條件下，目標強強度值隨入射角度曲線變化規律基本一致，不同的三種角反射器A3、B3、C3中，15kHz下目標強度值曲線A3目標強度值最大；

2）三面角反射器A3，在0°入射角度下出現第一個波峰，隨后在急劇衰減，達到最小值（A3最小值根據頻率由高到低分別在12°、18°、21°處取得），隨后緩滿增加，45°時取得出現第二個波峰；

3）三面角反射器B3，變化規律與A3相似，最大目標強度值在入射波0°時取得7.193dB，在45°時取得-0.998 dB，但最小值依次出現在9°、9°、18°處；

4）三面角反射器C3目標強度曲線較為復雜，入射頻率15kHz下在3°附近取得最大目標強度值2.888dB，隨后衰減并在45°附近取得最小目標強度值-5.763dB。10kHz下整體目標強度值曲線比15kHz大；

5）A3隨聲波入射方向改變的方向性較好，35°～55°波峰變化較為平緩，在此范圍內入射也可得到較高的目標強度值。B3方向性更好，但其整體目標強度值較小。

將三個角反射器在入射頻率為15kHz下目標強度值隨入射角度變化曲線進行匯總，如圖13所示。

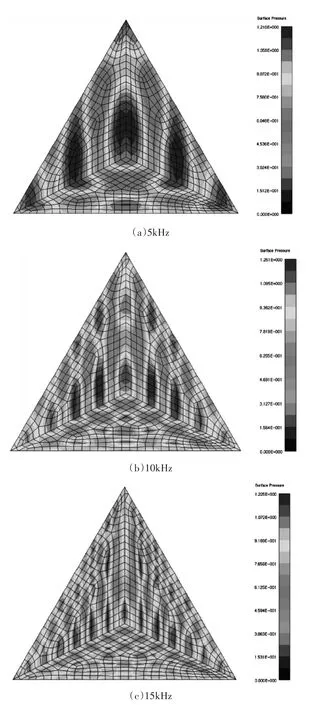
圖13 三面角反射器不同入射頻率下聲壓云紋圖

由圖12可知：

1）相同的入射聲源條件下，A3即正交三面角反射器的目標強度值隨入射角變化曲線，整體目標強度值大于B3、C3兩個角反射器；

2）C3三面角反射器隨入射角度的改變隨之減小，只在0°與90°下取得最大目標強度值，且散射寬度極小，因此實際使用價值小；

3）A3、B3三面角反射器在入射角度為 45°處有波峰，即在該處取得第二極大值，但B3在45°周圍取得的目標強度值較小。能滿足以45°為中點±10°入射范圍內目標強度值無太大波動，證明散射寬度較大，具有較強的方向性。

為進一步分析三面角反射器的聲散射特性，給出了聲波入射角度θ=90°、?=45°時的三面角角反射器表面聲壓分布圖（如圖13所示）。

由圖13可知，聲波在三面角反射器內發生了多次反射，聲壓值也呈帶狀分布，且相互平行，三面角反射器在內側以及Z方向平面上表面聲壓比較大，這是產生回波反射的主要原因。

4 結語

為分析實際生產導致的板間非正交誤差對剛性角反射器聲散射特性的影響，基于SYSNOISE邊界元軟件，對不同板間夾角的角反射器的遠場聲散射強度進行仿真計算，得到以下結論。

1）正交角反射器聲散射強度及散射寬度大于非正交角反射器，即板間非正交誤差會影響角反射器的性能；

2）二面角反射器在 θ =90°、? =0°～90°的入射條件下目標強度值隨入射角度變化曲線優于三面角反射器；

3）在實際應用中要盡量減小生產裝配帶來的誤差，盡可能使角反射器滿足正交的條件，使得其具有優異的聲散射特性。